1.填空题 进制转换Oct.2023
原题
部分可能会有用处的知识:
p p p进制转十进制:
假设有一个 p p p进制数,个位是 a 0 a_0 a0,向高位依次是 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,向低位依次是 b 1 , b 2 , b 3 , . . . , b k b_1,b_2,b_3,...,b_k b1,b2,b3,...,bk,那么它的整数部分就相当于 10 10 10进制中的
Σ i : 0 → n a i p i = a 0 × p 0 + a 1 × p 1 + . . . + a n × p n \Sigma_{i:0\rightarrow n}a_ip^i=a_0\times p^0+a_1\times p^1+...+a_n\times p^n Σi:0→naipi=a0×p0+a1×p1+...+an×pn
相应的,小数部分是
Σ i : 1 → n b i p − i = b 1 × p − 1 + b 2 × p − 2 + . . . + b n × p − n \Sigma_{i:1\rightarrow n}b_ip^{-i}=b_1\times p^{-1}+b_2\times p^{-2} +...+b_n\times p^{-n} Σi:1→nbip−i=b1×p−1+b2×p−2+...+bn×p−n
十进制转 p p p进制以此类推。例如,将 10 0 10 100_{10} 10010转换为 N 16 N_{16} N16:
- 将 100 100 100除以 16 16 16,得商 6 6 6,余数 4 4 4; ∴ \therefore ∴个位是 4 4 4
- 再将 6 6 6除以 16 16 16,得商 0 0 0,余数 6 6 6; ∴ 4 \therefore 4 ∴4的高一位是 6 6 6。
- ∴ 10 0 10 = 6 4 16 \therefore 100_{10}=64_{16} ∴10010=6416。
那么,如果想把 p p p进制和 q q q进制相转换,只需要借助十进制过渡一下即可。
在这里,我们约定, A = 10 , B = 11 , C = 12 , . . . , Z = 35 A=10,B=11,C=12,...,Z=35 A=10,B=11,C=12,...,Z=35
将 102 4 1048576 1024^{1048576} 10241048576进制下的 2 0 + 2 1 + 2 2 + . . . + 2 10485759 2 10485760 \dfrac{2^0+2^1+2^2+...+2^{10485759}}{2^{10485760}} 21048576020+21+22+...+210485759转为 [ ( 102 4 524288 + 1 ) ( 102 4 262144 + 1 ) ( 102 4 131072 + 1 ) ( 102 4 65536 + 1 ) . . ( 1024 − 1 ) + 2 ] [(1024^{524288}+1)(1024^{262144}+1)(1024^{131072}+1)(1024^{65536}+1)..(1024-1)+2] [(1024524288+1)(1024262144+1)(1024131072+1)(102465536+1)..(1024−1)+2]进制下的数字。
(为书写方便,约定 α = 1024 , β = 102 4 1048576 \alpha = 1024,\beta = 1024^{1048576} α=1024,β=10241048576, γ 1 = β − 1 \gamma_1=\beta-1 γ1=β−1, γ i = β − i \gamma_i=\beta-i γi=β−i。例如, 1024 × 1025 + 1024 1024\times1025+1024 1024×1025+1024在 1025 1025 1025进制中可以写作 α α \alpha\alpha αα)
解
对于 p p p进制显然 1 p − 1 = 0.1111111.... \frac{1}{p-1}=0.1111111.... p−11=0.1111111....
证明
p p p进制中,
0.11111... = p − 1 + p − 2 + . . . L e t S = p − 1 + p − 2 + . . . ∴ p S = S + 1 , p S − S = 1 ∴ ( p − 1 ) S = 1 ∴ S = 1 p − 1 0.11111...=p^{-1}+p^{-2}+...\\ Let\ S=p^{-1}+p^{-2}+...\\ \therefore pS=S+1,pS-S=1\\ \therefore (p-1)S=1\\ \therefore S=\frac{1}{p-1} 0.11111...=p−1+p−2+...Let S=p−1+p−2+...∴pS=S+1,pS−S=1∴(p−1)S=1∴S=p−11
令 p = 102 4 1048576 p=1024^{1048576} p=10241048576,化简原分式得 p − 1 p \frac{p-1}{p} pp−1
令 s = p + 1 = 102 4 1048576 + 1 , p = s − 1 s=p+1=1024^{1048576}+1,p=s-1 s=p+1=10241048576+1,p=s−1,原问题等同于求 s s s进制下的 s − 2 s − 1 \frac{s-2}{s-1} s−1s−2。
那么答案显然为 ( 102 4 1048576 − 1 ) × 0.1111... = 0. γ 1 γ 1 γ 1 . . . (1024^{1048576}-1)\times0.1111...=0.\gamma_1\gamma_1\gamma_1... (10241048576−1)×0.1111...=0.γ1γ1γ1...。
相关文章:

1.填空题 进制转换Oct.2023
原题 部分可能会有用处的知识: p p p进制转十进制: 假设有一个 p p p进制数,个位是 a 0 a_0 a0,向高位依次是 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,向低位依次是 b 1 , b 2 , b 3 , . . . …...
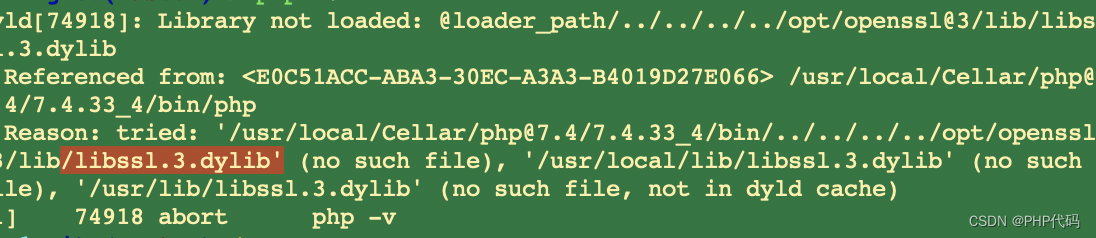
node 解决多版本配置 error:03000086:digital 引起的问题 已解决
在日常后端工作中,难免会安装前端的项目,今天有旧项目需要维护,但是 提示 node版本过高,或者不是长维护版本,部分分享说,加 opensll 过滤能解决,但是 还是不行,索性来这个 底朝天的找…...

前端面试题: js中对比两个对象的值是否相等? for..in 和 for...of的区别?
我去面试的时候会问这个问题, 而且发现不管是初级还是工作一段时间的小伙伴 都会说的不是很清晰 比如第一道题哈: 首先大部分人都会想起来 我们用JSON.stringify() 进行转换,查看两个是否相等 你敢说我下面的对象 值不是想等的吗。 但是你用…...

第十七章:Java连接数据库jdbc(java和myql数据库连接)
1.进入命令行:输入cmd,以管理员身份运行 windowsr 2.登录mysql 3.创建库和表 4.使用Java命令查询数据库操作 添加包 导入包的快捷键 选择第四个 找到包的位置 导入成功 创建java项目 二:连接数据库: 第一步:注册驱动…...
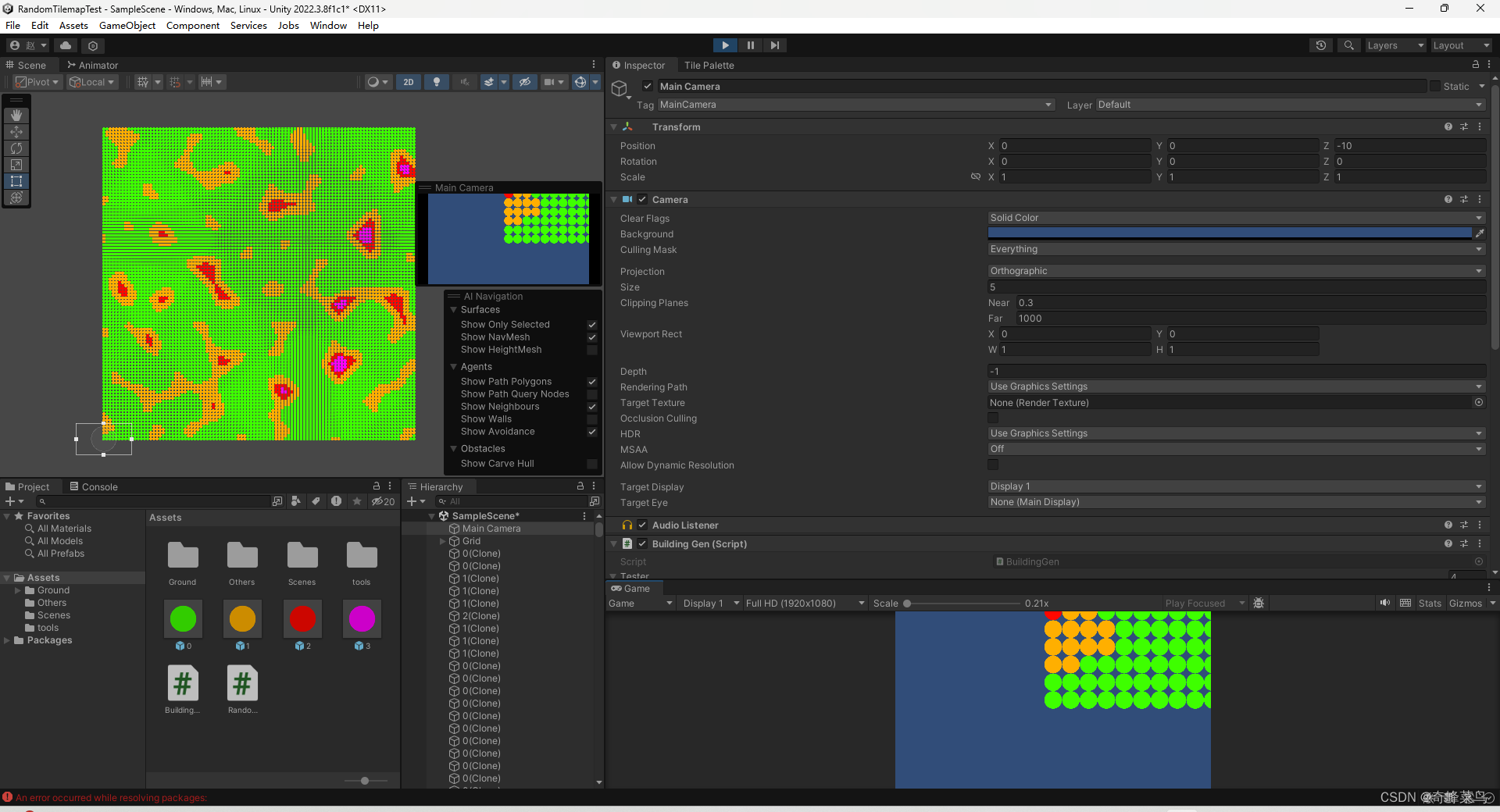
Unity基于种子与地块概率的开放世界2D地图生成
public class BuildingGen : MonoBehaviour {public int[] Building;//存储要生成的地块代码public int[] Probability;//存储概率public double seed;public int width 100;public int height 100;public float noiseScale 0.1f; //噪声缩放倍数private int[,] frequencyM…...
5.Vectors Transformation Rules
在上节,有个问题:向量分量的转换方式 与 新旧基底的转换方式相反 用例子来感受一下, 空间中一向量V,即该空间的一个基底:e1、e2 v e1 e2 现把基底 e1 、 e2 放大两倍。变成 基向量放大了两倍, 但对于…...

聊聊httpclient的CPool
序 本文主要研究一下httpclient的CPool ConnPool org/apache/http/pool/ConnPool.java public interface ConnPool<T, E> {/*** Attempts to lease a connection for the given route and with the given* state from the pool.** param route route of the connecti…...
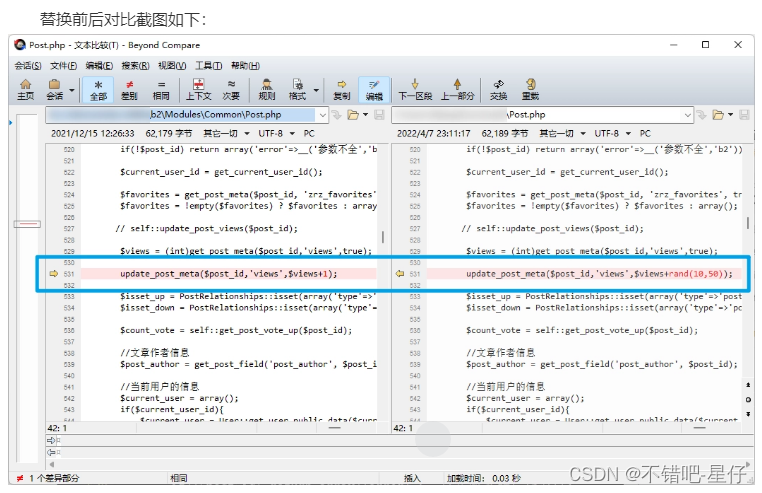
B2主题优化:WordPress文章每次访问随机增加访问量
老站长都知道,一个新站刚开始创建,内容也不多的时候,用户进来看到文章浏览量要么是0,要么是 个位数,非常影响体验,就会有一种“这个网站没人气,看来不行”的感觉。 即使你的内容做的很好&#x…...
大模型部署手记(1)ChatGLM2+Windows GPU
1.简介: 组织机构:智谱/清华 代码仓:https://github.com/THUDM/ChatGLM2-6B 模型:THUDM/chatglm2-6b 下载:https://huggingface.co/THUDM/chatglm2-6b 镜像下载:https://aliendao.cn/models/THUDM/chat…...

Rust Rocket: 构建Restful服务项目实战
前言 这几天我的笔记系统开发工作进入了搬砖期,前端基于Yew,后端基于Rocket。关于Rocket搭建Restful服务,官方也有介绍,感觉很多细节不到位。因此我打算花2到3天的时间来整理一下,也算是对自己的一个交代。 对于有一…...

苹果签名有多少种类之TF签名(TestFlight签名)是什么?优势是什么?什么场合需要应用到?
(一)TestFlight 能够让您:邀请内部和外部的测试人员为应用程序提供反馈。 跟踪应用程序在测试过程中发现的 bug 和用户体验问题。 收集 Crash 报告,了解应用程序在真实设备上的运行状况。 要使用 TestFlight,您可以按照…...

如何将图片存到数据库(以mysql为例), 使用ORM Bee更加简单
如何将图片存到数据库 1. 创建数据库: 2. 生成Javabean public class ImageExam implements Serializable {private static final long serialVersionUID 1596686274309L;private Integer id;private String name; // private Blob image;private InputStream image; //将In…...

【“栈、队列”的应用】408数据结构代码
王道数据结构强化课——【“栈、队列”的应用】代码,持续更新 链式存储栈(单链表实现),并基于上述定义,栈顶在链头,实现“出栈、入栈、判空、判满”四个基本操作 #include <stdio.h> #include <…...

es的nested查询
一、一层嵌套 mapping: PUT /nested_example {"mappings": {"properties": {"name": {"type": "text"},"books": {"type": "nested","properties": {"title": {"t…...
<一>Qt斗地主游戏开发:开发环境搭建--VS2019+Qt5.15.2
1. 开发环境概述 对于Qt的开发环境来说,主流编码IDE界面一般有两种:Qt Creator或VSQt。为了简单起见,这里的操作系统限定为windows,编译器也通用VS了。Qt版本的话自己选择就可以了,当然VS的版本也是依据Qt版本来选定的…...
)
python:进度条的使用(tqdm)
摘要:为python程序进度条,可以知道程序运行进度。 python中,常用的进度条模块是tqdm,将介绍tqdm的安装和使用 1、安装tqdm: pip install tqdm2、tqdm的使用: (1)在for循环中的使用࿱…...

Java类型转换和类型提升
目录 一、类型转换 1.1 自动类型转换(隐式) 1.1.1 int 与 long 之间 1.1.2 float 与 double 之间 1.1.3 int 与 byte 之间 1.2 强制类型转换(显示) 1.2.1 int 与 long 之间 1.2.2 float 与 double 之间 1.2.3 int 与 d…...

C# 读取 Excel xlsx 文件,显示在 DataGridView 中
编写 read_excel.cs 如下 using System; using System.Collections.Generic; using System.ComponentModel; using System.IO; using System.Data; using System.Linq; using System.Text; using System.Data.OleDb;namespace ReadExcel {public partial class Program{static…...

Docker02基本管理
目录 1、Docker 网络 1.1 Docker 网络实现原理 1.2 Docker 的网络模式 1.3 网络模式详解 1.4 资源控制 1.5 进行CPU压力测试 1.6 清理docker占用的磁盘空间 1.7 生产扩展 1、Docker 网络 1.1 Docker 网络实现原理 Docker使用Linux桥接,在宿主机虚拟一个Docke…...

Scala第十章
Scala第十章 章节目标 1.数组 2.元组 3.列表 4.集 5.映射 6.迭代器 7.函数式编程 8.案例:学生成绩单 scala总目录 文档资料下载...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
