python:进度条的使用(tqdm)
摘要:为python程序进度条,可以知道程序运行进度。
python中,常用的进度条模块是tqdm,将介绍tqdm的安装和使用
1、安装tqdm:
pip install tqdm
2、tqdm的使用:
(1)在for循环中的使用:
from tqdm import tqdmfor i in tqdm(range(10000)):print(i)
在for循环中使用tqdm是最常见了,因为知道循环的次数
(2)在while中使用tqdm
from tqdm import tqdmcount = 10000
pbar = tqdm(total = count)
i = 0
while i < count:print(i)i += 1pbar.update(1)
在while中使用进度条,也需要知道循环的次数,本人常在opencv处理视频中使用tqdm, 可大概知道处理的进度。
相关文章:
)
python:进度条的使用(tqdm)
摘要:为python程序进度条,可以知道程序运行进度。 python中,常用的进度条模块是tqdm,将介绍tqdm的安装和使用 1、安装tqdm: pip install tqdm2、tqdm的使用: (1)在for循环中的使用࿱…...

Java类型转换和类型提升
目录 一、类型转换 1.1 自动类型转换(隐式) 1.1.1 int 与 long 之间 1.1.2 float 与 double 之间 1.1.3 int 与 byte 之间 1.2 强制类型转换(显示) 1.2.1 int 与 long 之间 1.2.2 float 与 double 之间 1.2.3 int 与 d…...

C# 读取 Excel xlsx 文件,显示在 DataGridView 中
编写 read_excel.cs 如下 using System; using System.Collections.Generic; using System.ComponentModel; using System.IO; using System.Data; using System.Linq; using System.Text; using System.Data.OleDb;namespace ReadExcel {public partial class Program{static…...

Docker02基本管理
目录 1、Docker 网络 1.1 Docker 网络实现原理 1.2 Docker 的网络模式 1.3 网络模式详解 1.4 资源控制 1.5 进行CPU压力测试 1.6 清理docker占用的磁盘空间 1.7 生产扩展 1、Docker 网络 1.1 Docker 网络实现原理 Docker使用Linux桥接,在宿主机虚拟一个Docke…...

Scala第十章
Scala第十章 章节目标 1.数组 2.元组 3.列表 4.集 5.映射 6.迭代器 7.函数式编程 8.案例:学生成绩单 scala总目录 文档资料下载...

10.4 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、校招 | 集度2024届秋招正式启动(内推) 校招 | 集度2024届秋招正式启动(内推) 2、校招 | 道通科技2024秋季校园招聘正式启动啦! …...
从0开始深入理解并发、线程与等待通知机制(中)
一,深入学习 Java 的线程 线程的状态/生命周期 Java 中线程的状态分为 6 种: 1. 初始(NEW):新创建了一个线程对象,但还没有调用 start()方法。 2. 运行(RUNNABLE):Java 线程中将就绪(ready)和…...
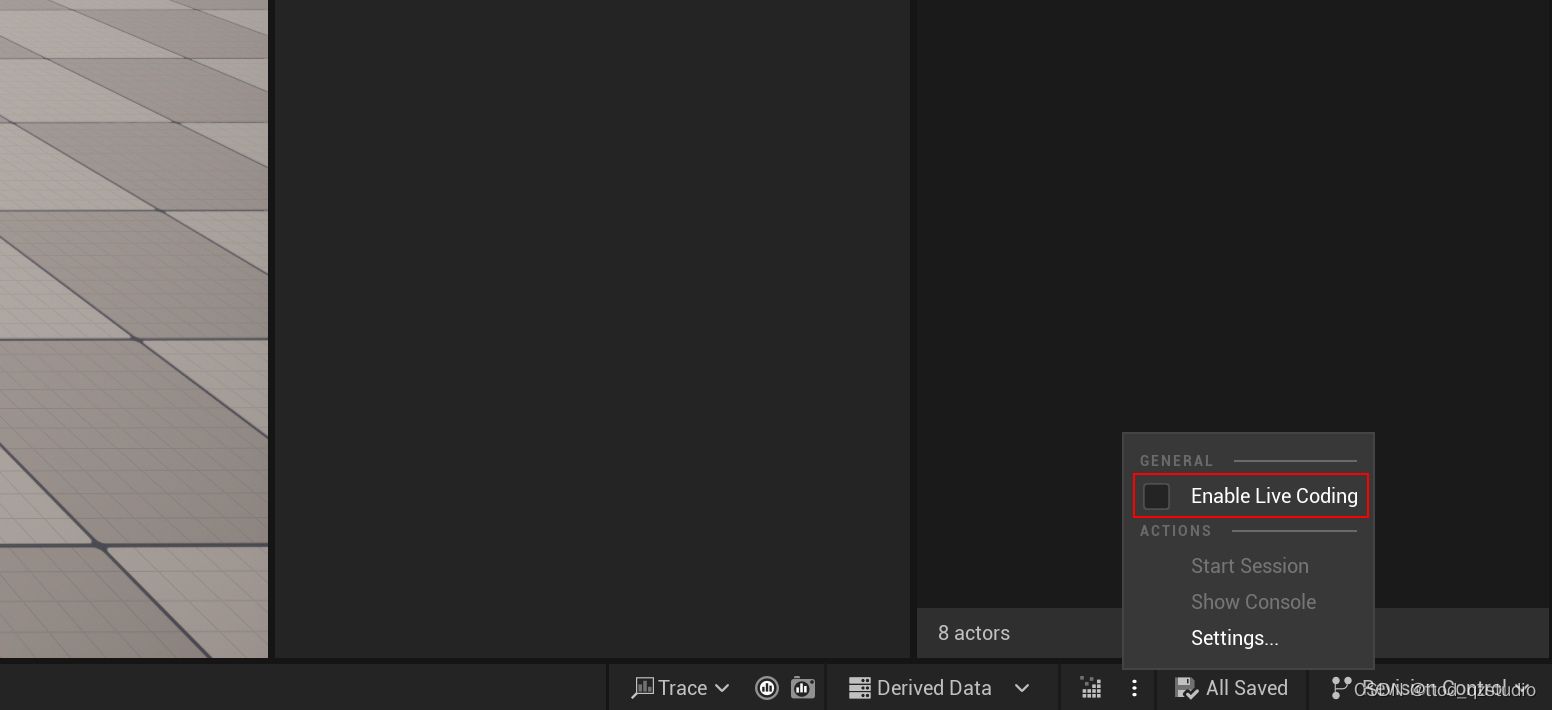
UE5报错及解决办法
1、编译报错,内容如下: Unable to build while Live Coding is active. Exit the editor and game, or press CtrlAltF11 if iterating on code in the editor or game 解决办法 取消Enable Live Coding勾选...
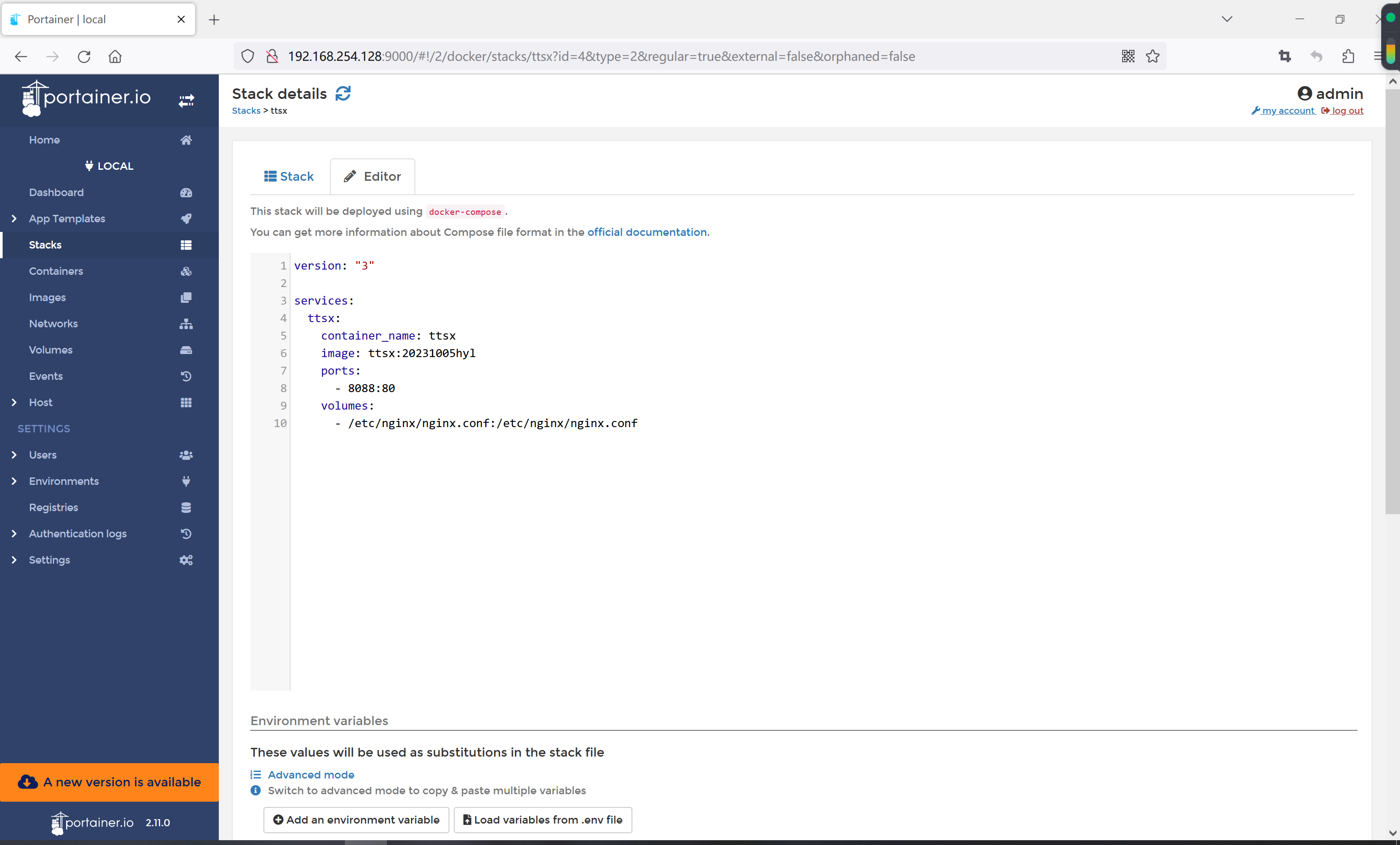
怎么通过docker/portainer部署vue项目
这篇文章分享一下如何通过docker将vue项目打包成镜像文件,并使用打包的镜像在docker/portainer上部署运行,写这篇文章参考了vue-cli和docker的官方文档。 首先,阅读vue-cli关于docker部署的说明,上面提供了关键的几个步骤。 从上面…...
【面试经典150 | 矩阵】旋转图像
文章目录 写在前面Tag题目来源题目解读解题思路方法一:原地旋转方法二:翻转代替旋转 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带…...
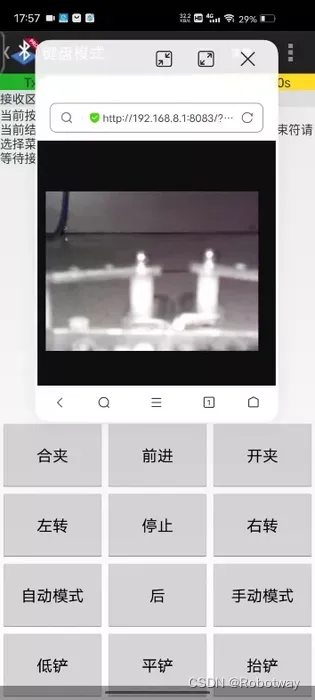
机器人制作开源方案 | 家庭清扫拾物机器人
作者:罗诚、李旭洋、胡旭、符粒楷 单位:南昌交通学院 人工智能学院 指导老师:揭吁菡 在家庭中我们有时无法到一些低矮阴暗的地方进行探索,比如茶几下或者床底下,特别是在部分家庭中,如果没有及时对这些阴…...

C++算法 —— 动态规划(8)01背包问题
文章目录 1、动规思路简介2、模版题:01背包第一问第二问优化 3、分割等和子集4、目标和5、最后一块石头的重量Ⅱ 背包问题需要读者先明白动态规划是什么,理解动规的思路,并不能给刚接触动规的人学习。所以最好是看了之前的动规博客࿰…...
ASUS华硕天选4笔记本FA507NU7735H_4050原装出厂Win11系统
下载链接:https://pan.baidu.com/s/1puxQOxk4Rbno1DqxhkvzXQ?pwdhkzz 系统自带网卡、显卡、声卡等所有驱动、出厂主题壁纸、Office办公软件、MyASUS华硕电脑管家、奥创控制中心等预装程序...

金蝶OA server_file 目录遍历漏洞
漏洞描述 金蝶OA server_file 存在目录遍历漏洞,攻击者通过目录遍历可以获取服务器敏感信息 漏洞影响 金蝶OA 漏洞复现 访问漏洞url: 漏洞POC Windows服务器: appmonitor/protected/selector/server_file/files?folderC://&suffi…...

read_image错误
File is no BMP-File(Halcon 错误代码5560)类似的错误一般都是图片内部封装的格式与外部扩展名不一致导致(也就是扩展名并不是真实图片的格式扩展)。 通过软件“UltraEdit”(http://www.onlinedown.net/soft/7752.htm)使用16进制查看&#x…...

文本分词排序
文本分词 在这个代码的基础上 把英语单词作为一类汉语,作为一类然后列出选项 1. 大小排序 2. 小大排序 3. 不排序打印保存代码 import jieba# 输入文本,让我陪你聊天吧~ lines [] print("请输入多行文本,以\"2333.3\"结束&am…...

SQL与关系数据库基本操作
SQL与关系数据库基本操作 文章目录 第一节 SQL概述一、SQL的发展二、SQL的特点三、SQL的组成 第二节 MySQL预备知识一、MySQL使用基础二、MySQL中的SQL1、常量(1)字符串常量(2)数值常量(3)十六进制常量&…...
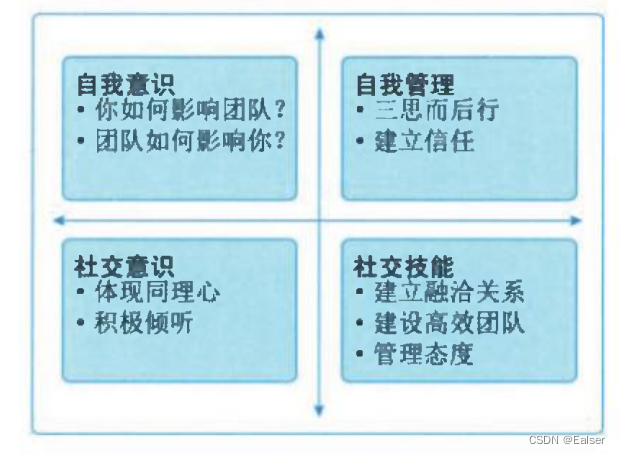
【2023年11月第四版教材】第18章《项目绩效域》(第一部分)
第18章《项目绩效域》(第一部分) 1 章节内容2 干系人绩效域2.1 绩效要点2.2 执行效果检查2.3 与其他绩效域的相互作用 3 团队绩效域3.1 绩效要点3.2 与其他绩效域的相互作用3.3 执行效果检查3.4 开发方法和生命周期绩效域 4 绩效要点4.1 与其他绩效域的相…...
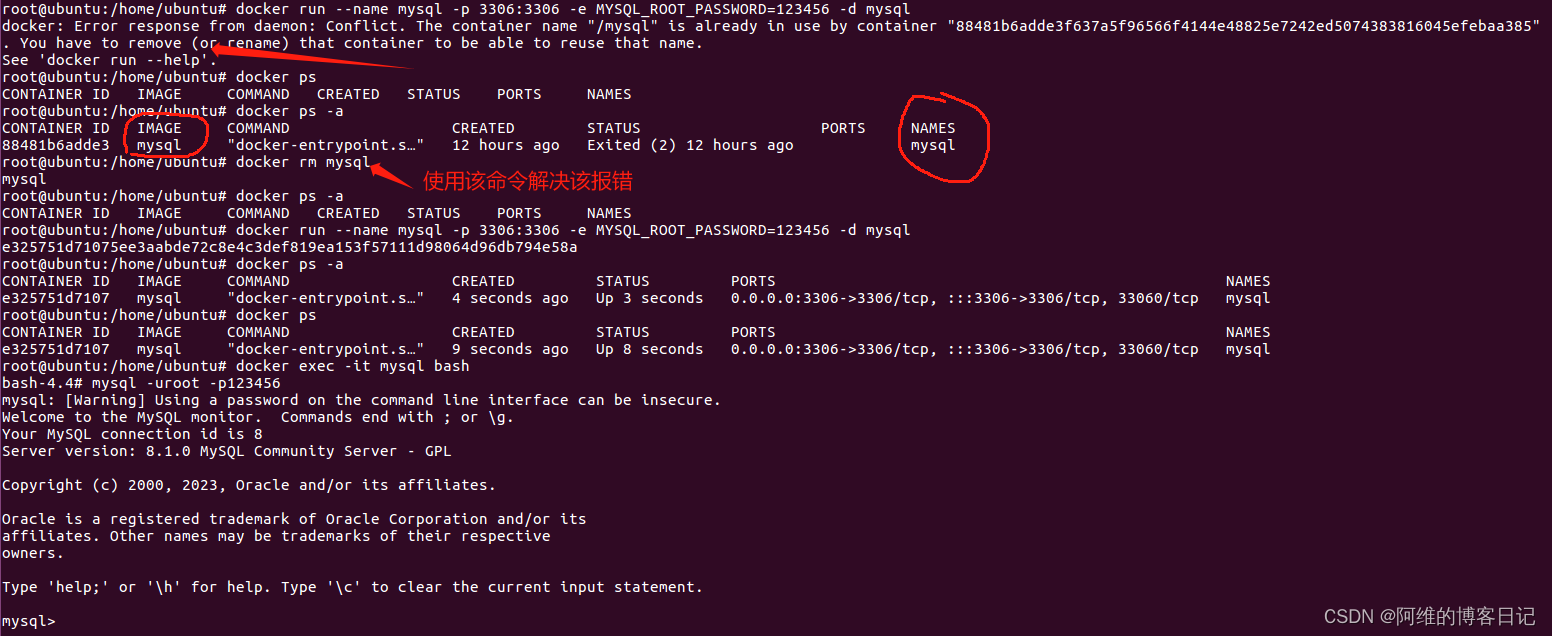
Docker启动Mysql
如果docker里面没有mysql需要先pull一个mysql镜像 docker pull mysql其中123456是mysql的密码 docker run --name mysql -p 3306:3306 -e MYSQL_ROOT_PASSWORD123456 -d mysql可以使用如下命令进入Mysql的命令行界面 docker exec -it mysql bash登录mysql使用如下命令,root是…...

QScrollArea样式
简介 QScrollBar垂直滚动条分为sub-line、add-line、add-page、sub-page、up-arrow、down-arrow和handle几个部分。 QScrollBar水平滚动条分为sub-line、add-line、add-page、sub-page、left-arrow、right-arrow和handle几个部分。 部件如下图所示: 样式详…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
