【面试经典150 | 矩阵】旋转图像
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:原地旋转
- 方法二:翻转代替旋转
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【原地操作】【数组】
题目来源
面试经典150 | 48. 旋转图像

题目解读
有一个二维矩阵,需要将二维矩阵顺时针旋转 90°,也就是行变到别的列(或者列变到别的行)操作。
解题思路
方法一:原地旋转
四位置元素交换
我们知道本题中的旋转操作就是将行和列进行相应的转换,具体的就是将 (i, j) 位置元素转移到 (j, n - 1 - i)位置,其中 n 为矩阵的行数(或者列数)。比如旋转操作会将第一行第二列位置的元素转移到第二行最后一列的位置。
题目中要求我们进行原地旋转,原地旋转就是在原矩阵中利用当前位置的元素去覆盖旋转后的位置,用原旋转后的位置元素去覆盖该旋转位置旋转后的位置…,如果进行四次旋转直到回到初始的位置。比如说现在的位置是 (i, j),记为位置 1:
(i, j)旋转后的位置为(j, n - 1 - i),记为位置2;(j, n - 1 - i)旋转后的位置为(n - 1- i, n - 1 - j),记为位置3;(n - 1- i, n - 1 - j)旋转后的位置为(n - 1 - j, i),记为位置4;
原地旋转操作就是实现以上四个位置元素的交换。交换示意图如下所示。
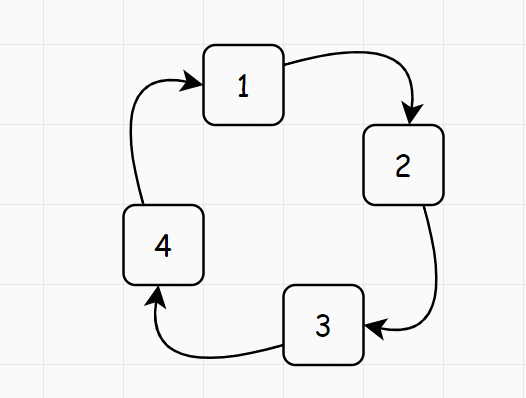
枚举的位置范围
当 n 为偶数的时候,我们需要枚举 n 2 / 4 = ( n / 2 ) × ( n / 2 ) n^2 / 4 = (n/2) \times (n/2) n2/4=(n/2)×(n/2) 个位置;
当 n 为奇数时,由于中心的位置经过旋转后位置不变,我们需要枚举 ( n 2 − 1 ) / 4 = ( ( n − 1 ) / 2 ) × ( ( n + 1 ) / 2 ) (n^2-1) / 4 = ((n-1)/2) \times ((n+1)/2) (n2−1)/4=((n−1)/2)×((n+1)/2) 个位置。
实现代码
class Solution {
public:void rotate(vector<vector<int>>& matrix) {// 原地操作int n = matrix.size();for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < (n + 1) / 2; ++j) {int temp = matrix[i][j];matrix[i][j] = matrix[n-j-1][i];matrix[n-j-1][i] = matrix[n-i-1][n-j-1];matrix[n-i-1][n-j-1] = matrix[j][n-i-1];matrix[j][n-i-1] = temp;}}}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2), n n n 为矩阵 matrix 的行数(列数)。
空间复杂度: O ( 1 ) O(1) O(1)。
方法二:翻转代替旋转
还有一种实现原地旋转的方法,那就是利用翻转来代替旋转。具体地:
首先对矩阵进行水平翻转(第一行变成最后一行,第二行变成倒数第二行,…),然后再对矩阵沿着主对角线方向进行翻转,这样就实现了矩阵顺时针旋转 90° 的操作了。
以上的翻转就是交换操作。
实现代码
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();// 水平翻转for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < n; ++j) {swap(matrix[i][j], matrix[n-1-i][j]);}}// 主对角线翻转for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {swap(matrix[i][j], matrix[j][i]);}}}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2), n n n 为矩阵 matrix 的行数(列数)。
空间复杂度: O ( 1 ) O(1) O(1)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 矩阵】旋转图像
文章目录 写在前面Tag题目来源题目解读解题思路方法一:原地旋转方法二:翻转代替旋转 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带…...
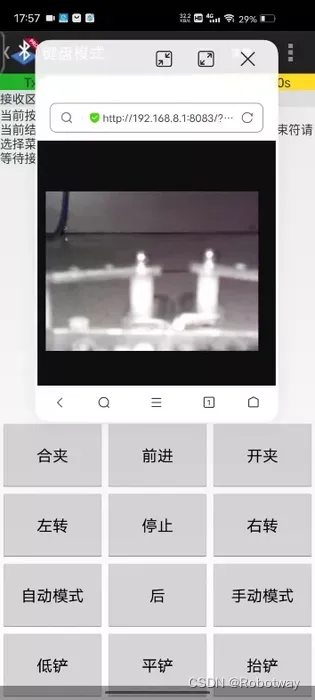
机器人制作开源方案 | 家庭清扫拾物机器人
作者:罗诚、李旭洋、胡旭、符粒楷 单位:南昌交通学院 人工智能学院 指导老师:揭吁菡 在家庭中我们有时无法到一些低矮阴暗的地方进行探索,比如茶几下或者床底下,特别是在部分家庭中,如果没有及时对这些阴…...

C++算法 —— 动态规划(8)01背包问题
文章目录 1、动规思路简介2、模版题:01背包第一问第二问优化 3、分割等和子集4、目标和5、最后一块石头的重量Ⅱ 背包问题需要读者先明白动态规划是什么,理解动规的思路,并不能给刚接触动规的人学习。所以最好是看了之前的动规博客࿰…...
ASUS华硕天选4笔记本FA507NU7735H_4050原装出厂Win11系统
下载链接:https://pan.baidu.com/s/1puxQOxk4Rbno1DqxhkvzXQ?pwdhkzz 系统自带网卡、显卡、声卡等所有驱动、出厂主题壁纸、Office办公软件、MyASUS华硕电脑管家、奥创控制中心等预装程序...

金蝶OA server_file 目录遍历漏洞
漏洞描述 金蝶OA server_file 存在目录遍历漏洞,攻击者通过目录遍历可以获取服务器敏感信息 漏洞影响 金蝶OA 漏洞复现 访问漏洞url: 漏洞POC Windows服务器: appmonitor/protected/selector/server_file/files?folderC://&suffi…...

read_image错误
File is no BMP-File(Halcon 错误代码5560)类似的错误一般都是图片内部封装的格式与外部扩展名不一致导致(也就是扩展名并不是真实图片的格式扩展)。 通过软件“UltraEdit”(http://www.onlinedown.net/soft/7752.htm)使用16进制查看&#x…...

文本分词排序
文本分词 在这个代码的基础上 把英语单词作为一类汉语,作为一类然后列出选项 1. 大小排序 2. 小大排序 3. 不排序打印保存代码 import jieba# 输入文本,让我陪你聊天吧~ lines [] print("请输入多行文本,以\"2333.3\"结束&am…...

SQL与关系数据库基本操作
SQL与关系数据库基本操作 文章目录 第一节 SQL概述一、SQL的发展二、SQL的特点三、SQL的组成 第二节 MySQL预备知识一、MySQL使用基础二、MySQL中的SQL1、常量(1)字符串常量(2)数值常量(3)十六进制常量&…...
【2023年11月第四版教材】第18章《项目绩效域》(第一部分)
第18章《项目绩效域》(第一部分) 1 章节内容2 干系人绩效域2.1 绩效要点2.2 执行效果检查2.3 与其他绩效域的相互作用 3 团队绩效域3.1 绩效要点3.2 与其他绩效域的相互作用3.3 执行效果检查3.4 开发方法和生命周期绩效域 4 绩效要点4.1 与其他绩效域的相…...
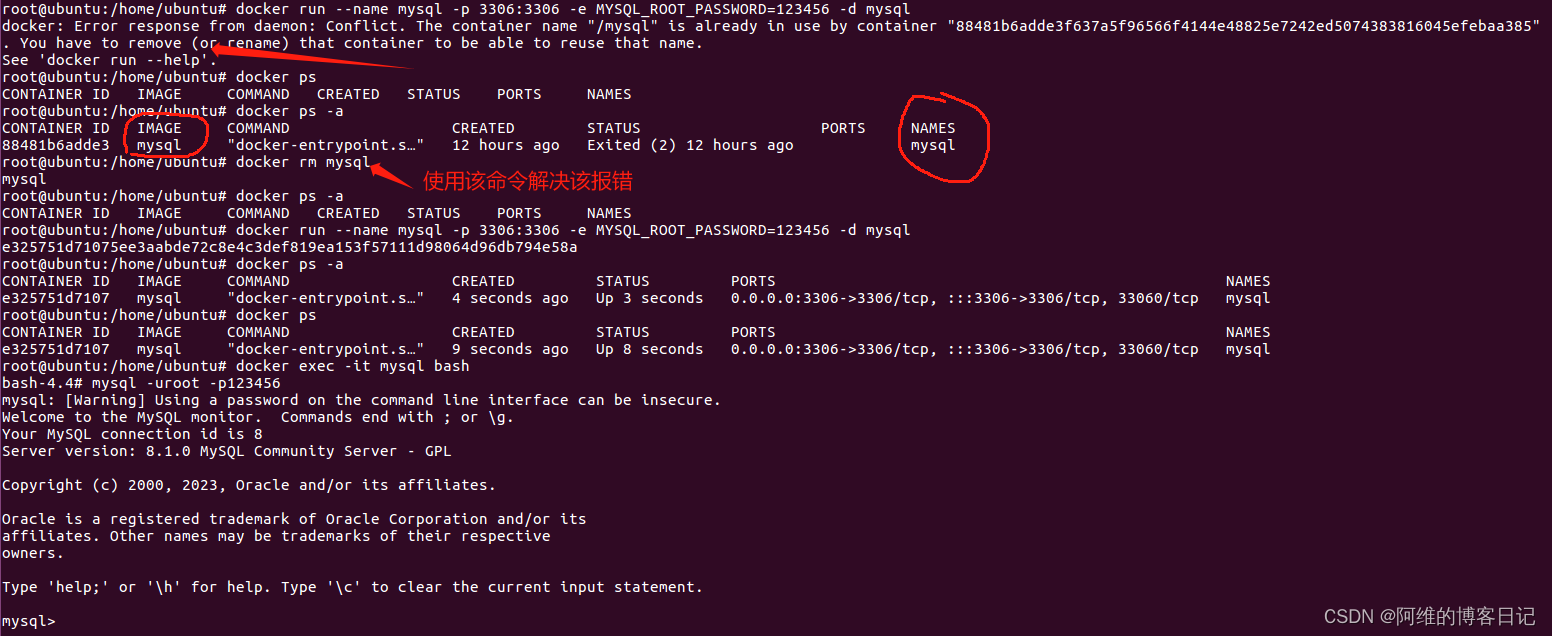
Docker启动Mysql
如果docker里面没有mysql需要先pull一个mysql镜像 docker pull mysql其中123456是mysql的密码 docker run --name mysql -p 3306:3306 -e MYSQL_ROOT_PASSWORD123456 -d mysql可以使用如下命令进入Mysql的命令行界面 docker exec -it mysql bash登录mysql使用如下命令,root是…...

QScrollArea样式
简介 QScrollBar垂直滚动条分为sub-line、add-line、add-page、sub-page、up-arrow、down-arrow和handle几个部分。 QScrollBar水平滚动条分为sub-line、add-line、add-page、sub-page、left-arrow、right-arrow和handle几个部分。 部件如下图所示: 样式详…...
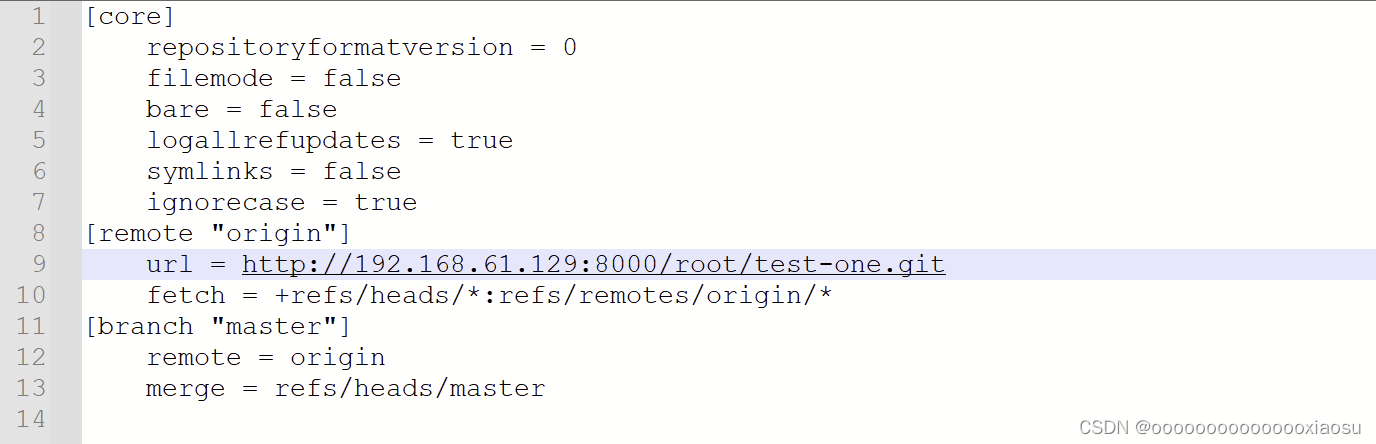
【gitlab】git push -u origin master 报403
问题描述 gitlab版本:14.0.5 虚拟机版本:centos7 项目:renren-fast 原因分析 .git -> config目录下 url配错 但这个url不是手动配置的,还不知道怎么生成。 解决方法 把配置错误的url改成gitlab的project的url 这样&#…...

第二篇:矩阵的翻转JavaScript
一维数组的翻转 // 一维矩阵翻转 // 实例: arr [1,2,3,4,5] > [5,4,3,2,1] let n readline() let arr readline().split( ).map(Number) // console.log(n,arr) let temp 0 for(let i 0; i < n/2;i){temp arr[i]arr[i] arr[n-i-1]arr[n-i-1] temp }…...
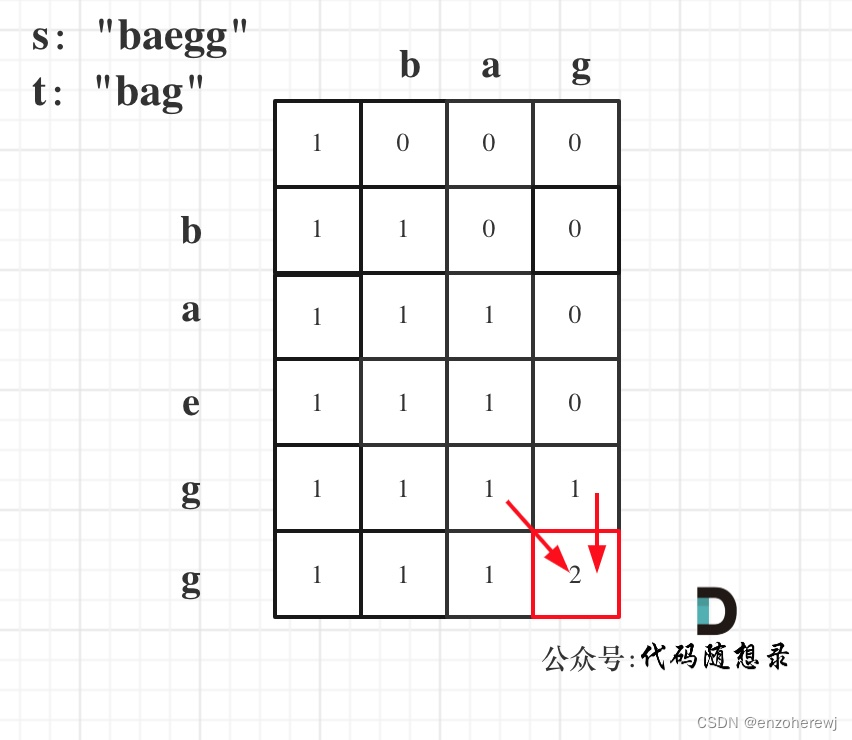
代码随想录算法训练营第五十七天 | 动态规划 part 15 | 392.判断子序列、115.不同的子序列
目录 392.判断子序列思路代码 115.不同的子序列思路代码 392.判断子序列 Leetcode 思路 dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]递推公式: 初始化:为0遍历顺序ÿ…...

【国漫逆袭】人气榜,小医仙首次上榜,霍雨浩排名飙升,不良人热度下降
Hello,小伙伴们,我是小郑继续为大家深度解析国漫资讯。 为了提升作品和角色的讨论度,增加平台的用户活跃度,小企鹅推出了动漫角色榜,该榜单以【年】【周】【日】为单位,通过角色的点赞量和互动量进行排名 上周的动漫角…...

国庆中秋特辑(七)Java软件工程师常见20道编程面试题
以下是中高级Java软件工程师常见编程面试题,共有20道。 如何判断一个数组是否为有序数组? 答案:可以通过一次遍历,比较相邻元素的大小。如果发现相邻元素的大小顺序不对,则数组不是有序数组。 public boolean isSort…...
长剖与贪心+树上反悔贪心:1004T4
长剖的本质是一种贪心。(启发式合并本质也是类似哈夫曼树的过程) 在此题中,首先肯定变直径,然后选端点为根。然后选叶子。而每个叶子为了不重复计算,可以只计算其长剖后所在链的贡献。(本题精髓࿰…...

二叉树经典例题
前言: 本文主要讲解了关于二叉树的简单经典的例题。 因为二叉树的特性,所以关于二叉树的大部分题目,需要利用分治的思想去递归解决问题。 分治思想: 把大问题化简成小问题(根节点、左子树、右子树)&…...

什么是指针的指针和指向函数的指针?
理解指针的指针和指向函数的指针对于C语言初学者来说可能会有些挑战,但它们都是非常重要的概念,可以帮助你更好地理解和利用C语言的强大功能。在本文中,我将详细解释这两个概念,包括它们的概念、用途和示例。 指针的指针…...
多个excel合并
目的:将同一个文件下的多个 “京东差评.xlsx” 合并为一个:“京东汇总.xlsx" 代码如下: # -*- coding: utf-8 -*- """ Created on Wed Oct 4 12:52:32 2023author: 64884 """import pandas as pd impor…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
