代码随想录算法训练营第五十七天 | 动态规划 part 15 | 392.判断子序列、115.不同的子序列

392.判断子序列

Leetcode

思路

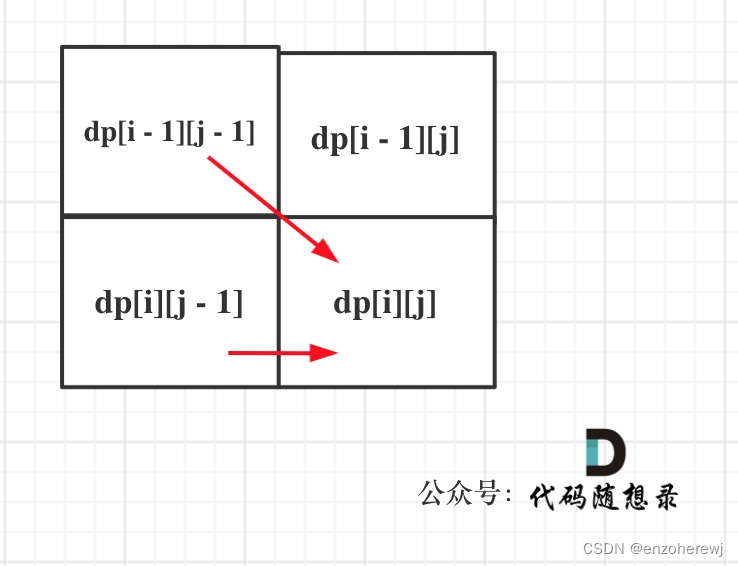
1. dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]
2. 递推公式：
   
3. 初始化：为0
4. 遍历顺序：从上到下，从左到右
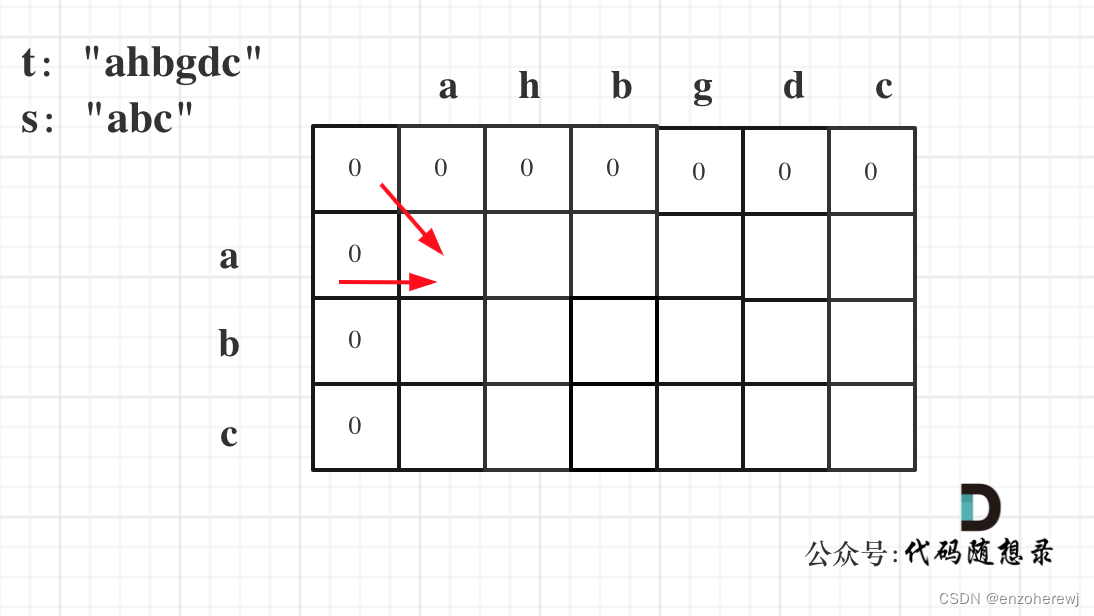
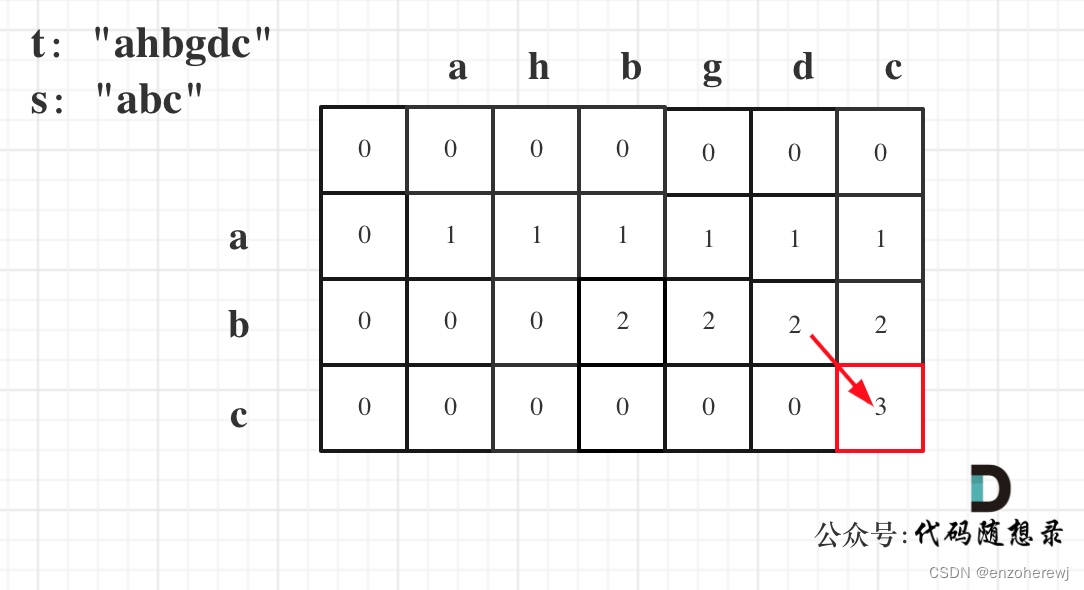
5. 举例：输入：s = “abc”, t = “ahbgdc”，dp状态转移图如下：
   
   

代码

class Solution:def isSubsequence(self, s: str, t: str) -> bool:dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]for i in range(1, len(s) + 1):for j in range(1, len(t) + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = dp[i][j - 1]return dp[-1][-1] == len(s)

• 时间复杂度：O(n × m)
• 空间复杂度：O(n × m)

115.不同的子序列

Leetcode

思路

1. dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
2. 递推公式：
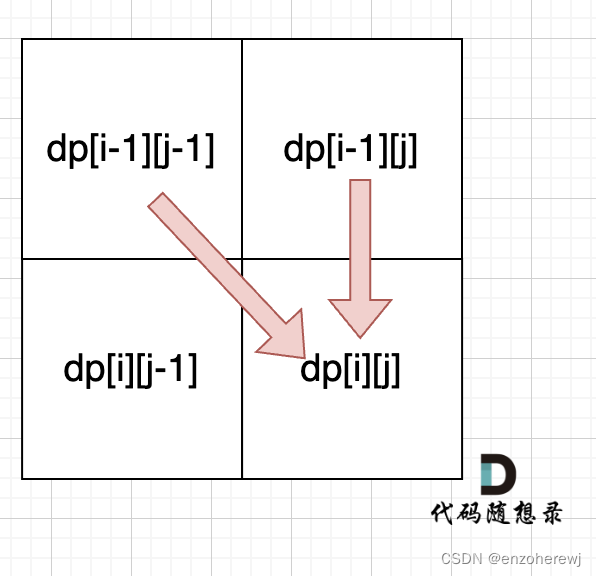
   • 当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
   • 当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j], 所以递推公式为：dp[i][j] = dp[i - 1][j]
3. 初始化：从递推公式中看出，左上方和上方是需要初始化的，dp[i][0] 和dp[0][j]是一定要初始化的。dp[i][0] = 1, dp[0][j] = 0, dp[0][0] = 1。
   
   
4. 遍历顺序：从上到下，从左到右
5. 举例推导：以s：“baegg”，t："bag"为例，推导dp数组状态如下：
   

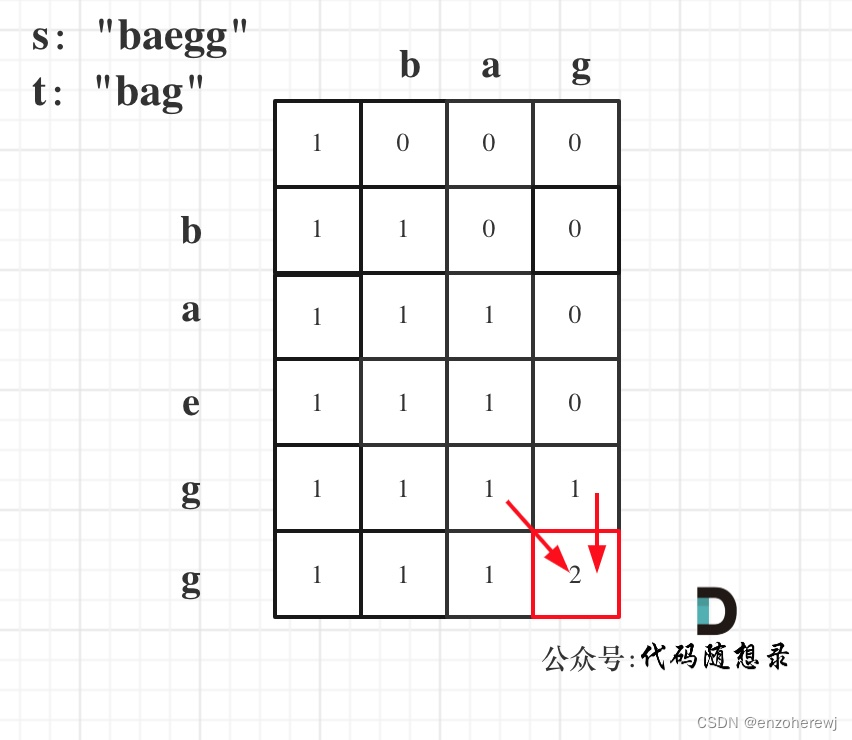
代码

class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]for i in range(len(s) + 1):dp[i][0] = 1for i in range(1, len(s) + 1):for j in range(1, len(t) + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1]else:dp[i][j] = dp[i - 1][j]return dp[-1][-1]

• 时间复杂度：O(n × m)
• 空间复杂度：O(n × m)