【算法|动态规划No.12】leetcode152. 乘积最大子数组
个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
目录
- 1️⃣题目描述
- 2️⃣题目解析
- 3️⃣解题代码
1️⃣题目描述
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
注意:
1 <= nums.length <= 2 * 104-10 <= nums[i] <= 10nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
2️⃣题目解析
虽然本题目要求的是求取乘积最大子数组,但是我们还得把乘积最小的情况求取出来。为什么呢?因为不只是正数 * 正数 > 0,还有负数 * 负数 = 正数的情况。
状态表示:
f[i]表示以i位置为结尾的所有子数组的最大乘积g[i]表示以i位置为结尾的所有子数组的最小乘积
状态转移方程:
f[i] = max(max(nums[i],f[i - 1] * nums[i - 1]),g[i - 1] * nums[i - 1]);g[i] = min(min(nums[i],f[i - 1] * nums[i - 1]),g[i - 1] * nums[i - 1]);
3️⃣解题代码
class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> f(n+1);auto g = f;f[0] = g[0] = 1;int ret = INT_MIN;for(int i = 1;i <= n;i++){int a = nums[i - 1];int b = f[i - 1] * nums[i - 1];int c = g[i - 1] * nums[i - 1];f[i] = max(max(a,b),c);g[i] = min(min(a,b),c);ret = max(ret,f[i]);}return ret;}
};
通过啦!!!
相关文章:

【算法|动态规划No.12】leetcode152. 乘积最大子数组
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...
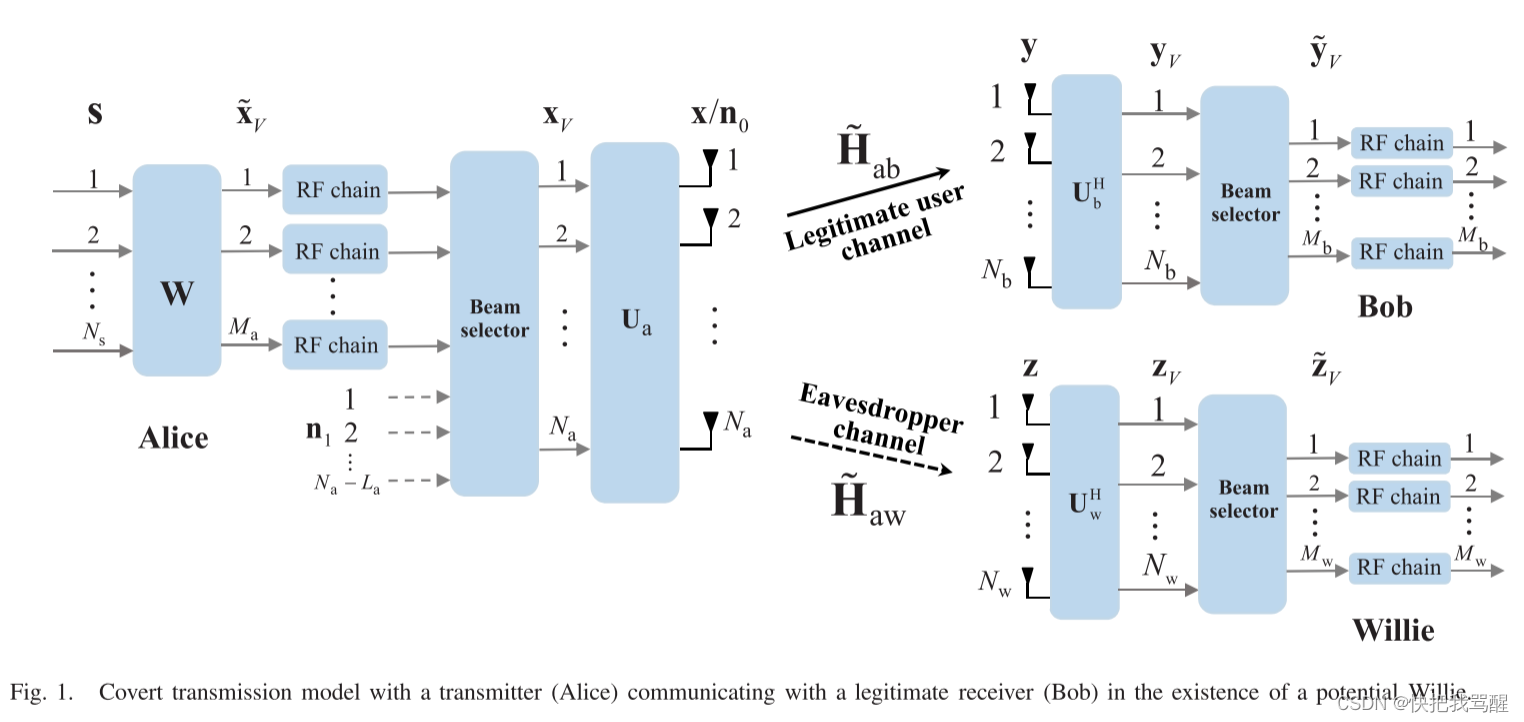
Covert Communication 与选择波束(毫米波,大规模MIMO,可重构全息表面)
Covert Communication for Spatially Sparse mmWave Massive MIMO Channels 2023 TOC abstract 隐蔽通信,也称为低检测概率通信,旨在为合法用户提供可靠的通信,并防止任何其他用户检测到合法通信的发生。出于下一代通信系统安全链路的强烈…...

计算机毕业设计 基于协调过滤算法的绿色食品推荐系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
华为云云耀云服务器L实例评测|部署在线影音媒体系统 Jellyfin
华为云云耀云服务器L实例评测|部署在线影音媒体系统 Jellyfin 一、云耀云服务器L实例介绍1.1 云服务器介绍1.2 产品规格1.3 应用场景1.4 支持镜像 二、云耀云服务器L实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置 三、部署 Jellyfin3.1 Jellyfin 介绍3.2 Docke…...
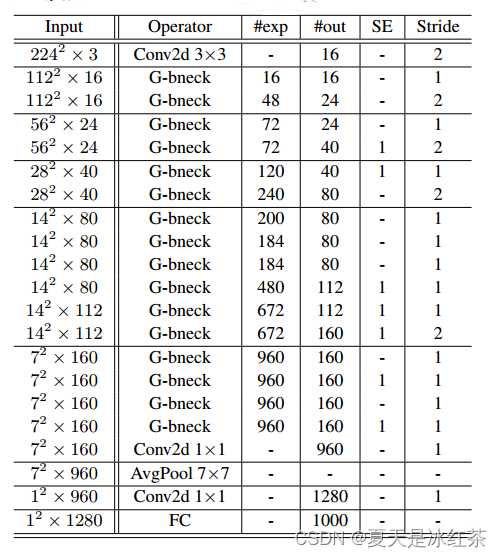
GhostNet原理解析及pytorch实现
论文:https://arxiv.org/abs/1911.11907 源码:https://github.com/huawei-noah/ghostnet 简要论述GhostNet的核心内容。 Ghost Net 1、Introduction 在训练良好的深度神经网络的特征图中,丰富甚至冗余的信息通常保证了对输入数据的全面理…...
视频二维码的制作方法,支持内容修改编辑
现在学生经常会需要使用音视频二维码,比如外出打开、才艺展示、课文背诵等等。那么如何制作一个可以长期使用的二维码呢?下面来给大家分享一个二维码制作(免费在线二维码生成器-二维码在线制作-音视频二维码在线生成工具-机智熊二维码&#x…...

清华GLM部署记录
环境部署 首先安装anaconda(建议包管理比较方便)windows用户需手动配置一下环境变量,下面默认是在ubuntu环境说明创建python环境,conda create -n your_env_name python3.10 (注:官方是提供是python3.8,但…...

贪心算法+练习
正值国庆之际,祝愿祖国繁荣昌盛,祝愿朋友一生平安!终身学习,奋斗不息! 目录 1.贪心算法简介 2.贪心算法的特点 3.如何学习贪心算法 题目练习(持续更新) 1.柠檬水找零(easy&…...
使用华为eNSP组网试验⑷-OSPF多区域组网
今天进行了OSPF的多区域组网试验,本来这是个很简单的操作,折腾了好长时间,根本原因只是看了别人写的配置代码,没有真正弄明白里面对应的规则。 一般情况下,很多单位都使用OSPF进行多区域的组网,大体分为1个…...

P1843 奶牛晒衣服 【贪心】
P1843 奶牛晒衣服 【贪心】 题目背景 熊大妈决定给每个牛宝宝都穿上可爱的婴儿装 。但是由于衣服很湿,为牛宝宝晒衣服就成了很不爽的事情。于是,熊大妈请你(奶牛)帮助她完成这个重任。 题目描述 一件衣服在自然条件下用一秒的时间…...
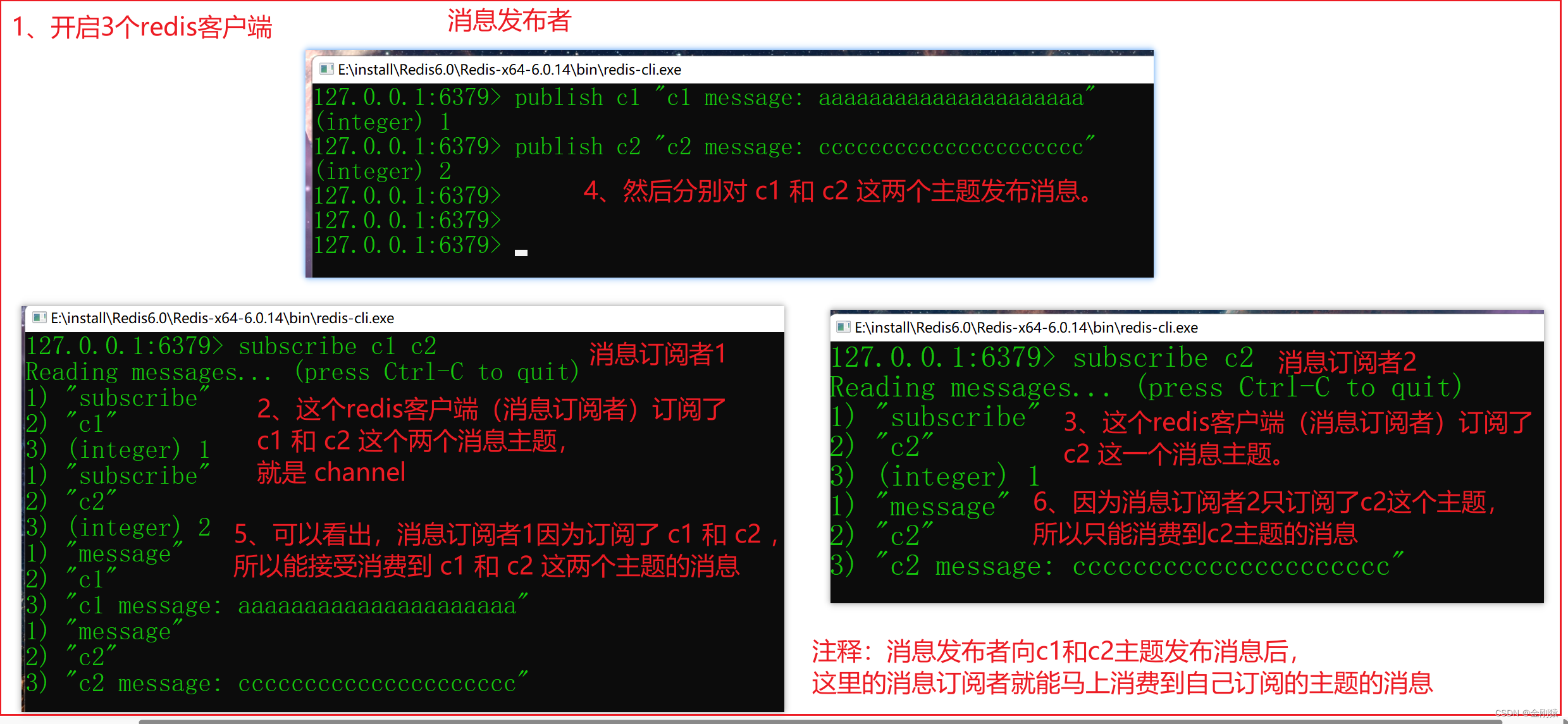
91、Redis - 事务 与 订阅-发布 相关的命令 及 演示
★ 事务相关的命令 Redis事务保证事务内的多条命令会按顺序作为整体执行,其他客户端发出的请求绝不可能被插入到事务处理的中间, 这样可以保证事务内所有命令作为一个隔离操作被执行。 Redis事务同样具有原子性,事务内所有命令要么全部被执…...
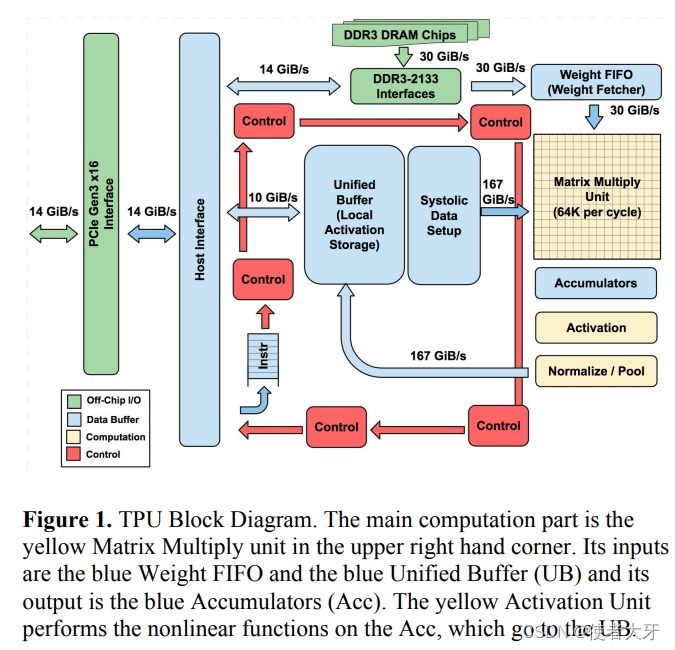
GPU如何成为AI的加速器
0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。 本文关键词:GPU、深度学习、GP…...

Map声明、元素访问及遍历、⼯⼚模式、实现 Set - GO语言从入门到实战
Map声明、元素访问及遍历 - GO语言从入门到实战 Map 声明的方式 m := map[string]int{"one": 1, "two": 2, "three": 3} //m初始化时就已经设置了3个键值对,所以它的初始长度len(m)是3。m1 := map[string]int{} //m1被初始化为一个空的m…...
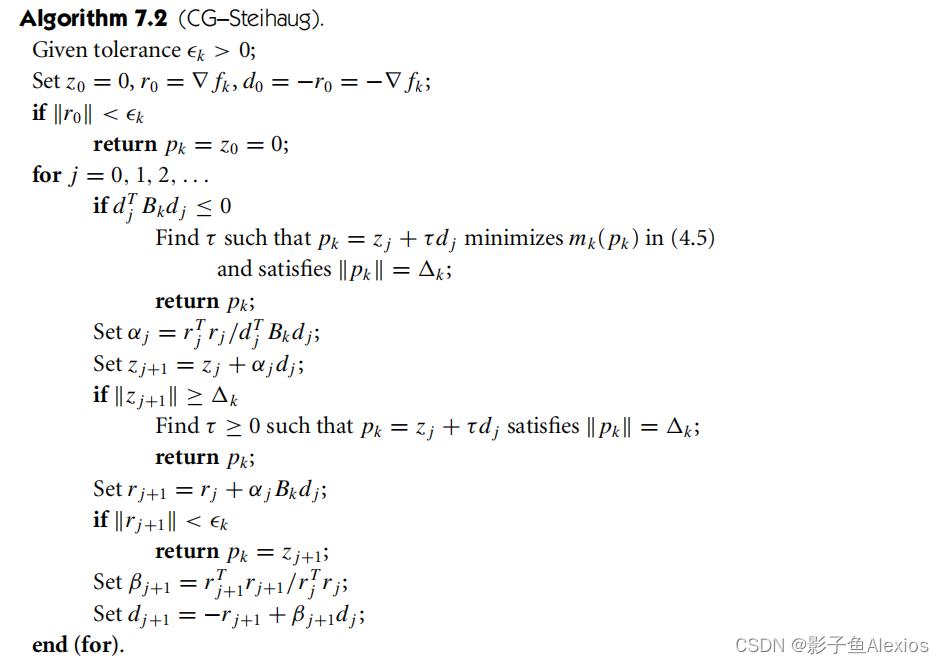
机器人中的数值优化|【七】线性搜索牛顿共轭梯度法、可信域牛顿共轭梯度法
机器人中的数值优化|【七】线性搜索牛顿共轭梯度法、可信域牛顿共轭梯度法 Line Search Newton-CG, Trust Region Newton-CG 往期回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbro…...

websocket实现go(server)与c#(client)通讯
go 服务端 使用到github.com/gorilla/websocket package mainimport ("fmt""github.com/gorilla/websocket""log""net/http" )func main() {var upgrader websocket.Upgrader{ReadBufferSize: 1024,WriteBufferSize: 1024,CheckOr…...

洛谷题目题解详细解答
洛谷是一个很不错的刷题软件,可是找不到合适的题解是个大麻烦,大家有啥可以私信问我,以下是我已经通过的题目。 你如果有哪一题不会(最好是我通过过的,我没过的也没关系),可以私信我࿰…...
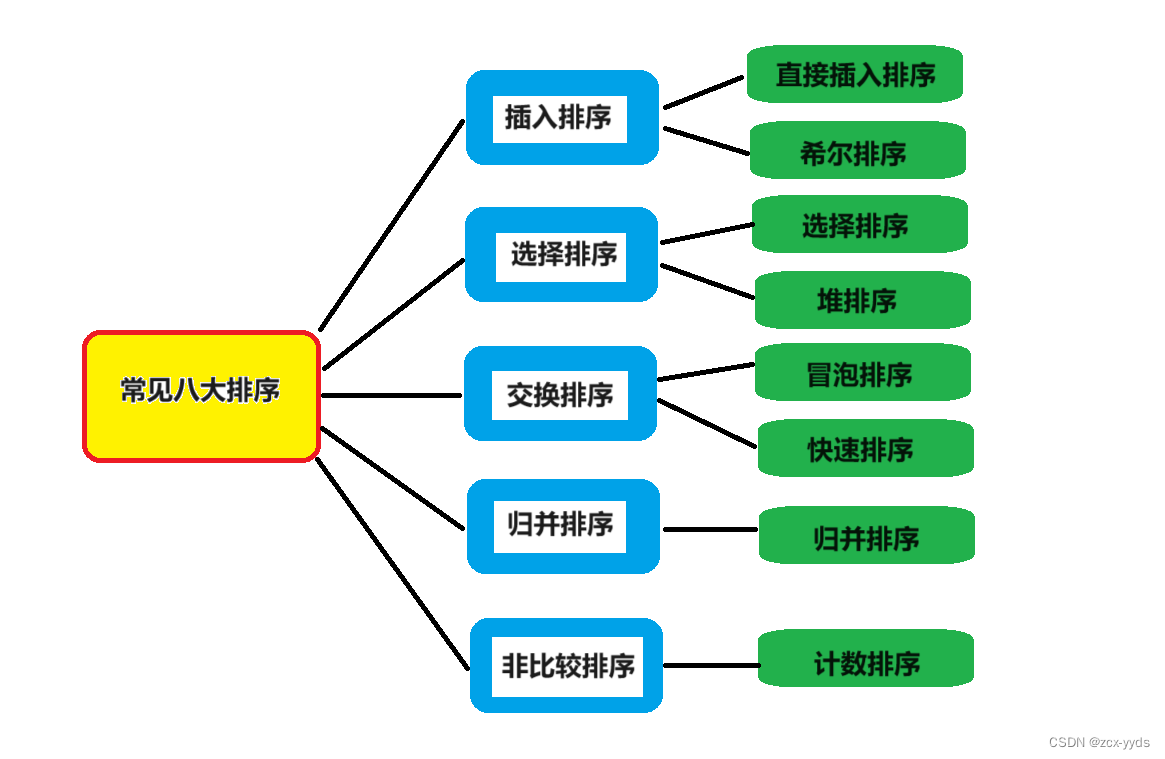
【C语言】八大排序算法
文章目录 一、冒泡排序1、定义2、思想及图解3、代码 二、快速排序1、hoare版本2、挖坑法3、前后指针法4、非递归快排5、快速排序优化1)三数取中选key值2)小区间优化 三、直接插入排序1、定义2、代码 四、希尔排序1、定义2、图解3、代码 五、选择排序1、排…...

2023年中国智能电视柜产量、需求量、市场规模及行业价格走势[图]
电视柜是随着电视机的发展和普及而演变出的家具种类,其主要作用是承载电视机,又称视听柜,随着生活水平的提高,与电视机相配套的电器设备也成为电视柜的收纳对象。 随着智能家具的发展,智能电视机柜的造型和风格都是有了…...

docker容器使用初体验
我们写程序时,都会搭建相关的环境,比如写了一个web,使用了tomcat、nginx等,现在想要把程序部署到云服务器或者在其他电脑上运行,就需要重新部署一遍环境,尤其是项目开源后,上手成本大。 docker…...

React Hooks ——性能优化Hooks
什么是Hooks Hooks从语法上来说是一些函数。这些函数可以用于在函数组件中引入状态管理和生命周期方法。 React Hooks的优点 简洁 从语法上来说,写的代码少了上手非常简单 基于函数式编程理念,只需要掌握一些JavaScript基础知识与生命周期相关的知识不…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

