堆的初步认识
在学习本节文章前要先了解:大顶堆与小顶堆: (优先级队列_加瓦不加班的博客-CSDN博客)
堆实现
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。
什么叫完全二叉树?
答:
1.除了最后一层不用满足有两个分支,其他层都要满足有两个分支
2.如果再往完全二叉树中加一个节点,那么必须靠左添加,从左往右依次填满,左边没有填满之前,右边就不能填,如图:
添加前:
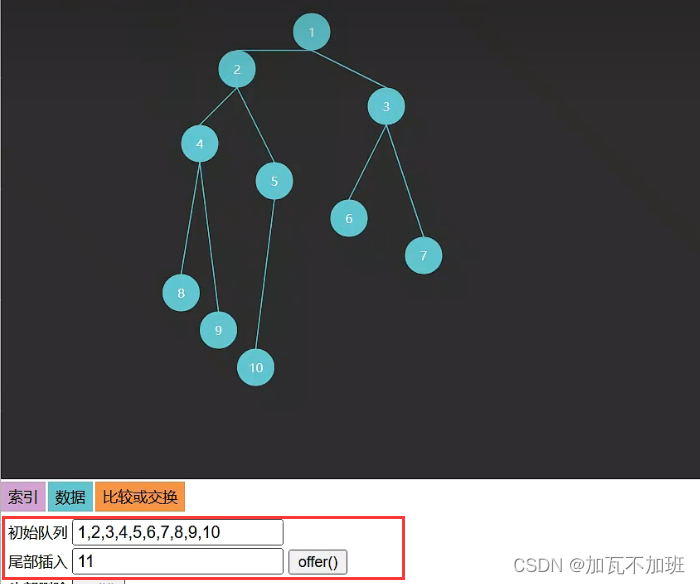
添加后:

堆的特性如下:堆分为两种:大顶堆与小顶堆
在大顶堆中,任意节点 C 与它的父节点 P 符合 P.value >= C.value:父节点的值>=子节点的值
而小顶堆中,任意节点 C 与它的父节点 P 符合 P.value <= C.value:父节点的值<=子节点的值
最顶层的节点(没有父亲)称之为 root 根节点
例1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的

例2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐

大顶堆
大顶堆中,任意节点 C 与它的父节点 P 符合 P.value >= C.value:父节点的值>=子节点的值
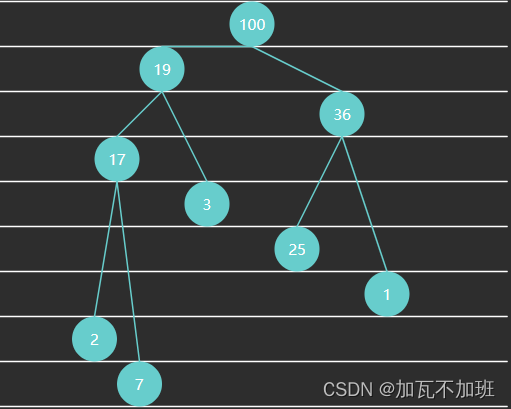
代码实现:
/*** @BelongsProject: arithmetic* @BelongsPackage: com.hzp.algorithm.heap* @Author: ASUS* @CreateTime: 2023-10-02 10:41* @Description: TODO 大顶堆Plus_增加了堆化等方法* @Version: 1.0*/
public class MaxHeap {int[] array;int size;public MaxHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//注意:当传入的数组是null时,我们可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int top = array[0];swap(0, size - 1);size--;//从索引位置0开始下潜down(0);return top;}private boolean isEmpty(){if(size==0){return true;}return false;}/*** 删除指定索引处元素 这个方法与删除堆顶元素方法思路一样** @param index 索引* @return 被删除元素*/public int poll(int index) {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}//向堆的尾部添加元素: 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered > array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MaxHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 :套用公式 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int max = parent;//left < size:必须是有效的索引 不可能超出数组最大长度吧if (left < size && array[left] > array[max]) {max = left;}if (right < size && array[right] > array[max]) {max = right;}if (max != parent) { // 找到了更大的孩子swap(max, parent);down(max);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {
// int[] array = {1, 2, 3, 4, 5, 6, 7};
// MaxHeap maxHeap = new MaxHeap(array);
// System.out.println(Arrays.toString(maxHeap.array));//TODO 利用堆来实现排序//1. heapify 建立大顶堆//2. 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆//3. 重复第二步直至堆里剩一个元素int[] array = {1, 2, 3, 4, 5, 6, 7};//1. heapify 建立大顶堆MaxHeap maxHeap = new MaxHeap(array);System.out.println(Arrays.toString(maxHeap.array));//3. 重复第二步直至堆里剩一个元素while(maxHeap.size>1){//将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆maxHeap.swap(0, maxHeap.size-1);maxHeap.size--;maxHeap.down(0);}System.out.println(Arrays.toString(maxHeap.array));}
}
小顶堆
小顶堆中,任意节点 C 与它的父节点 P 符合 P.value <= C.value:父节点的值<=子节点的值
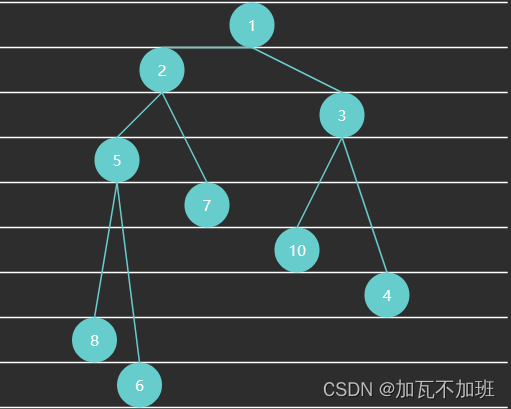
代码实现:
/*** @BelongsProject: arithmetic* @BelongsPackage: com.hzp.algorithm.heap* @Author: ASUS* @CreateTime: 2023-10-02 10:41* @Description: TODO 小顶堆Plus_增加了堆化等方法* @Version: 1.0*/
public class MinHeap {int[] array;int size;public MinHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//注意:当传入的数组是null时,我们可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int top = array[0];swap(0, size - 1);size--;//从索引位置0开始下潜down(0);return top;}private boolean isEmpty(){if(size==0){return true;}return false;}public boolean isFull(){return size==array.length;}/*** 删除指定索引处元素 这个方法与删除堆顶元素方法思路一样** @param index 索引* @return 被删除元素*/public int poll(int index) {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行if(isEmpty()){throw new IllegalArgumentException("数组有问题");}int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}//向堆的尾部添加元素: 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered < array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MinHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 :套用公式 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int min = parent;//left < size:必须是有效的索引 不可能超出数组最大长度吧if (left < size && array[left] < array[min]) {min = left;}if (right < size && array[right] < array[min]) {min = right;}if (min != parent) { // 找到了更大的孩子swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {
// int[] array = {1, 2, 3, 4, 5, 6, 7};
// MaxHeap maxHeap = new MaxHeap(array);
// System.out.println(Arrays.toString(maxHeap.array));//1. heapify 建立小顶堆//2. 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆//3. 重复第二步直至堆里剩一个元素int[] array = {1, 2, 3, 4, 5, 6, 7};//1. heapify 建立大顶堆MinHeap maxHeap = new MinHeap(array);System.out.println(Arrays.toString(maxHeap.array));//3. 重复第二步直至堆里剩一个元素while(maxHeap.size>1){//将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆maxHeap.swap(0, maxHeap.size-1);maxHeap.size--;maxHeap.down(0);}System.out.println(Arrays.toString(maxHeap.array));}
}
完全二叉树可以使用数组来表示

那完全二叉树显然是个非线性的数据结构,但是它存储的时候可以使用线性的数组结构来存储数据:

特征
如果从索引 0 开始存储节点数据
节点 i 的父节点为 floor((i-1)/2),当 i>0 时
节点 i 的左子节点为 2i+1,右子节点为 2i+2,当然它们得 < size
如果从索引 1 开始存储节点数据
节点 i 的父节点为 floor(i/2),当 i > 1 时
节点 i 的左子节点为 2i,右子节点为 2i+1,同样得 < size
堆的优化
以大顶堆为例,相对于之前的优先级队列,增加了堆化等方法:
public class MaxHeap {int[] array;int size;public MaxHeap(int capacity) {this.array = new int[capacity];}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {//注意:当传入的数组是null时,我们可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行int top = array[0];swap(0, size - 1);size--;//从索引位置0开始下潜down(0);return top;}/*** 删除指定索引处元素 这个方法与删除堆顶元素方法思路一样** @param index 索引* @return 被删除元素*/public int poll(int index) {//注意:当传入的数组是null,可以设置一个判断来抛个异常,在这里我们就不去判断,请有需要的自行int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素* @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered);size++;return true;}//向堆的尾部添加元素: 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;if (offered > array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public MaxHeap(int[] array) {this.array = array;this.size = array.length;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 :套用公式 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int max = parent;//left < size:必须是有效的索引 不可能超出数组最大长度吧if (left < size && array[left] > array[max]) {max = left;}if (right < size && array[right] > array[max]) {max = right;}if (max != parent) { // 找到了更大的孩子swap(max, parent);down(max);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}public static void main(String[] args) {int[] array = {1, 2, 3, 4, 5, 6, 7};MaxHeap maxHeap = new MaxHeap(array);System.out.println(Arrays.toString(maxHeap.array));}
}Floyd 建堆算法作者(也是之前龟兔赛跑判环作者):
如果对龟兔赛跑判环不了解的可以查看此文章:

-
找到最后一个非叶子节点 (叶子节点:没有孩子的节点)
-
从后向前,对每个节点执行下潜
一些规律
-
一棵满二叉树节点个数为 2^h-1,如下例中高度 h=3 节点数是 2^3-1=7
-
非叶子节点范围为 [0, size/2-1]
算法时间复杂度分析

下面看交换次数的推导:设节点高度为 3

每一层的交换次数为:节点个数*此节点交换次数,总的交换次数为

即 h:总高度 i:本层高度

在 Wolfram|Alpha: Computational Intelligence 输入
Sum[\(40)Divide[Power[2,x],Power[2,i]]*\(40)i-1\(41)\(41),{i,1,x}]
推导出
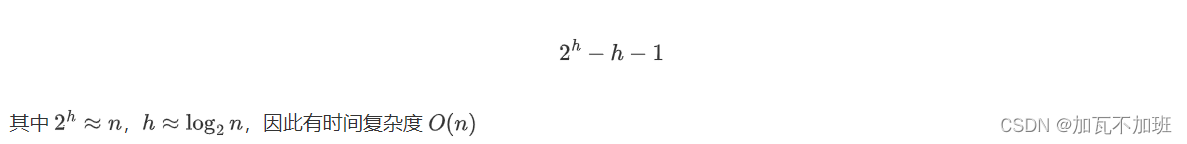
通用堆
通用heap :可以扩容的 heap, max 用于指定是大顶堆还是小顶堆
/*** @BelongsProject: arithmetic* @BelongsPackage: com.hzp.algorithm.heap* @Author: ASUS* @CreateTime: 2023-10-02 15:56* @Description: TODO 通用heap :可以扩容的 heap, max 用于指定是大顶堆还是小顶堆* @Version: 1.0*/
public class Heap {int[] array;int size;boolean max;public int size() {return size;}//当max为true则为大顶堆 如果是false则为小顶堆public Heap(int capacity, boolean max) {this.array = new int[capacity];this.max = max;}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {int top = array[0];swap(0, size - 1);size--;down(0);return top;}/*** 删除指定索引处元素** @param index 索引* @return 被删除元素*/public int poll(int index) {int deleted = array[index];swap(index, size - 1);size--;down(index);return deleted;}/*** 替换堆顶元素** @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素*/public void offer(int offered) {if (size == array.length) {grow();}up(offered);size++;}//如果容量不够就进行扩容private void grow() {int capacity = size + (size >> 1);int[] newArray = new int[capacity];//将原有的数组重新放到扩容好的数组中System.arraycopy(array, 0,newArray, 0, size);array = newArray;}// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered) {int child = size;while (child > 0) {int parent = (child - 1) / 2;boolean cmp = max ? offered > array[parent] : offered < array[parent];if (cmp) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}public Heap(int[] array, boolean max) {this.array = array;this.size = array.length;this.max = max;heapify();}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int min = parent;if (left < size && (max ? array[left] > array[min] : array[left] < array[min])) {min = left;}if (right < size && (max ? array[right] > array[min] : array[right] < array[min])) {min = right;}if (min != parent) { // 找到了更大的孩子swap(min, parent);down(min);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}}
相关文章:
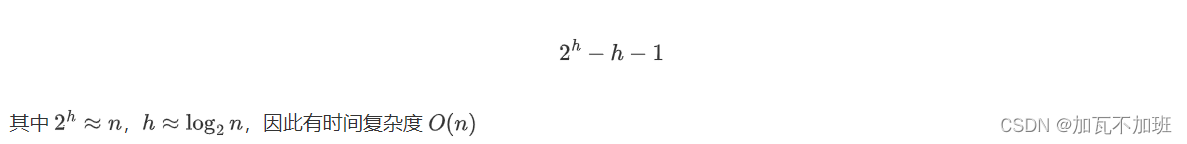
堆的初步认识
在学习本节文章前要先了解:大顶堆与小顶堆: (优先级队列_加瓦不加班的博客-CSDN博客) 堆实现 计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。 什么叫完全二叉树? 答&#x…...

CycleGAN模型之Pytorch实战
一、CycleGAN基本介绍 1. CycleGAN论文:《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》 2. 原文代码:https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix 3. 网传精简代码:https://github.com/aitorzip/PyTorch-CycleGAN …...
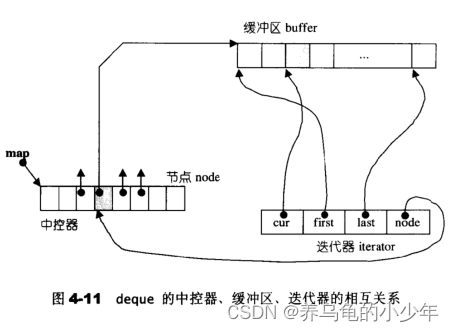
C++(STL容器适配器)
前言: 适配器也称配接器(adapters)在STL组件的灵活组合运用功能上,扮演着轴承、转换器的角色。 《Design Patterns》对adapter的定义如下:将一个class的接口转换为另一个class的接口,使原本因接口不兼容而…...
)
软考 系统架构设计师系列知识点之软件架构风格(7)
接前一篇文章:软考 系统架构设计师系列知识点之软件架构风格(6) 这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格(水平)考试,11月4号就要考试,因此…...

【Vue3】自定义指令
除了 Vue 内置的一系列指令 (比如 v-model 或 v-show) 之外,Vue 还允许你注册自定义的指令 (Custom Directives)。 1. 生命周期钩子函数 一个自定义指令由一个包含类似组件生命周期钩子的对象来定义。钩子函数会接收到指令所绑定元素作为其参数。 在 <script …...

UG\NX CAM二次开发 加工模块获取 UF _ask_application_module
文章作者:代工 来源网站:NX CAM二次开发专栏 简介: UG\NX CAM二次开发 加工模块获取 UF _ask_application_module 代码: void MyClass::do_it() { // TODO: add your code here // 获取NX当前所在的模块 int module_id = 0; // UF_ask_application_module(&…...

借助GPU算力编译Android
借助GPU算力编译Android 借助GPU编译Android代码的意义在于提高编译的效率和速度。传统的CPU编译方式在处理大量代码时可能会遇到性能瓶颈,而GPU编译利用了显卡的并行计算能力,可以同时处理多个任务,加快编译过程。通过利用GPU的并行计算能力,可以将编译过程中的多个任务分…...

docker-compose一键部署mysql
1.创建安装目录 mnt为硬盘挂载目录,根据实际情况修改 mkdir -p /mnt/mysql cd /mnt/mysql vim docker-compose.yml2.编写docker-compose.yml version: 3.1 services:db:image: mysql:5.7 #mysql版本volumes:- ./data/db:/var/lib/mysql #数据文件- ./etc/my.cnf:/…...
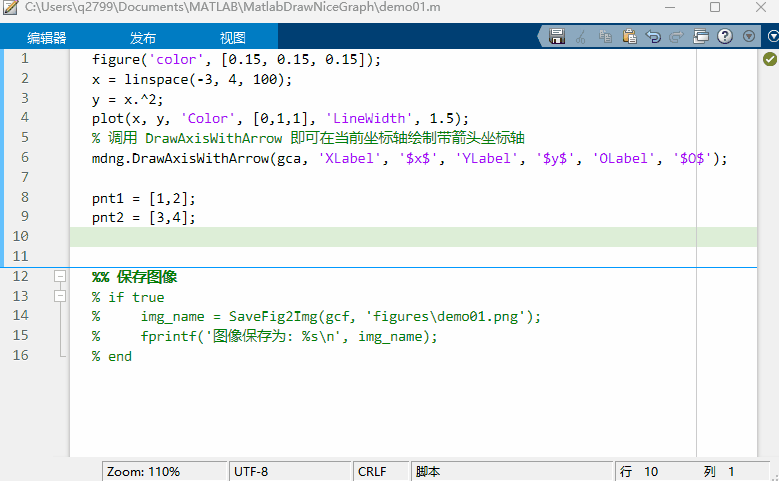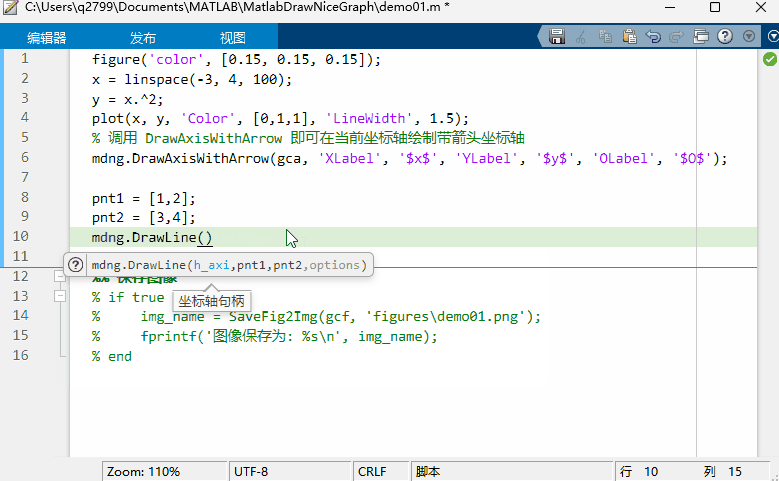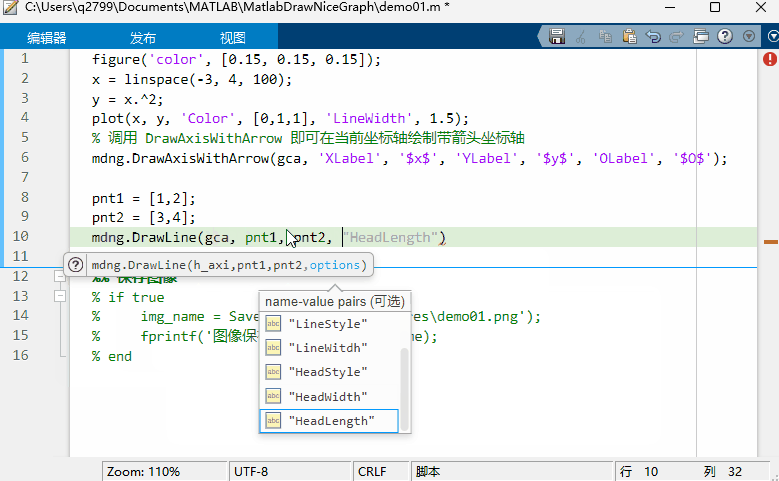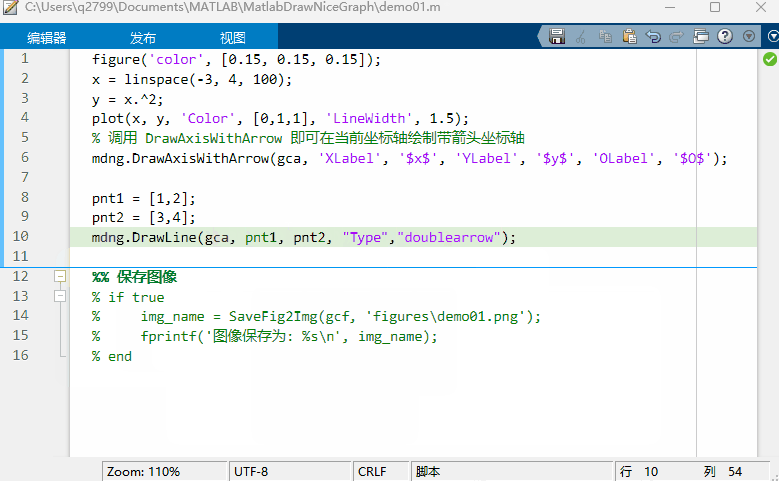
MATLAB 函数签名器
文章目录 MATLAB 函数签名器注释规范模板参数类型 kind数据格式 type选项的支持 使用可执行程序封装为m函数程序输出 编译待办事项推荐阅读附录 MATLAB 函数签名器 MATLAB 函数签名器 (FUNCSIGN) ,在规范注释格式的基础上为函数文件或类文件自动生成函数签名&#…...
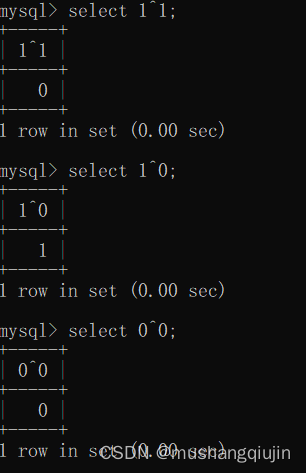
2019强网杯随便注bugktu sql注入
一.2019强网杯随便注入 过滤了一些函数,联合查询,报错,布尔,时间等都不能用了,尝试堆叠注入 1.通过判断是单引号闭合 ?inject1-- 2.尝试堆叠查询数据库 ?inject1;show databases;-- 3.查询数据表 ?inject1;show …...

Html+Css+Js计算时间差,返回相差的天/时/分/秒(从未来的一个日期时间到当前日期时间的差)。
Html部分 <!DOCTYPE html> <html><head><meta charset"utf-8" /><title></title><link rel"stylesheet" type"text/css" href"css/index.css" /><script src"js/index.js" t…...
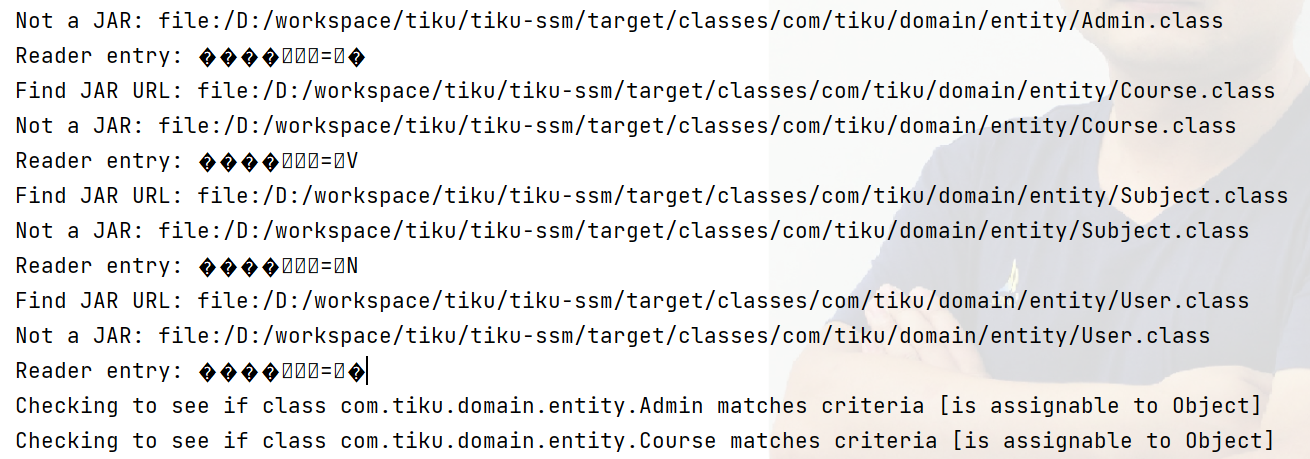
mybatis项目启动报错:reader entry: ���� = v
问题再现 解决方案一 由于指定的VFS没有找,mybatis启用了默认的DefaultVFS,然后由于DefaultVFS的内部逻辑,从而导致了reader entry乱码。 去掉mybatis配置文件中关于别名的配置,然后在mapper.xml文件中使用完整的类名。 待删除的…...

【GIT版本控制】--什么是版本控制
一、为什么需要版本控制? 版本控制是在软件开发和许多其他领域中非常重要的工具,因为它解决了许多与协作、追踪更改和管理项目相关的问题。以下是一些主要原因,解释了为什么需要版本控制: 追踪更改历史: 版本控制系统允许您准确…...

ChatGPT付费创作系统V2.3.4独立版 +WEB端+ H5端 + 小程序最新前端
人类小徐提供的GPT付费体验系统最新版系统是一款基于ThinkPHP框架开发的AI问答小程序,是基于国外很火的ChatGPT进行开发的Ai智能问答小程序。当前全民热议ChatGPT,流量超级大,引流不要太简单!一键下单即可拥有自己的GPT࿰…...

GEE16: 区域日均降水量计算
Precipitation 1. 区域日均降水量计算2. 降水时间序列3. 降水数据年度时间序列对比分析 1. 区域日均降水量计算 今天分析一个计算区域日均降水量的方法: 数据信息: Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) is a…...
打开MySQL数据库
在命令行里输入mysql --version就可以查看: mysql -uroot -p之前设置的密码(不用输入)就可登录成功:...
玩转ChatGPT:DALL·E 3生成图像
一、写在前面 好久不更新咯,因为没有什么有意思的东西分享的。 今天更新,是因为GPT整合了自家的图像生成工具,名字叫作DALLE 3。 DALLE 3是OpenAI推出的一种生成图像的模型,它基于GPT-3架构进行训练,但是它的主要目…...
小程序入门笔记(一) 黑马程序员前端微信小程序开发教程
微信小程序基本介绍 小程序和普通网页有以下几点区别: 运行环境:小程序可以在手机的操作系统上直接运行,如微信、支付宝等;而普通网页需要在浏览器中打开才能运行。 开发技术:小程序采用前端技术进行开发,…...
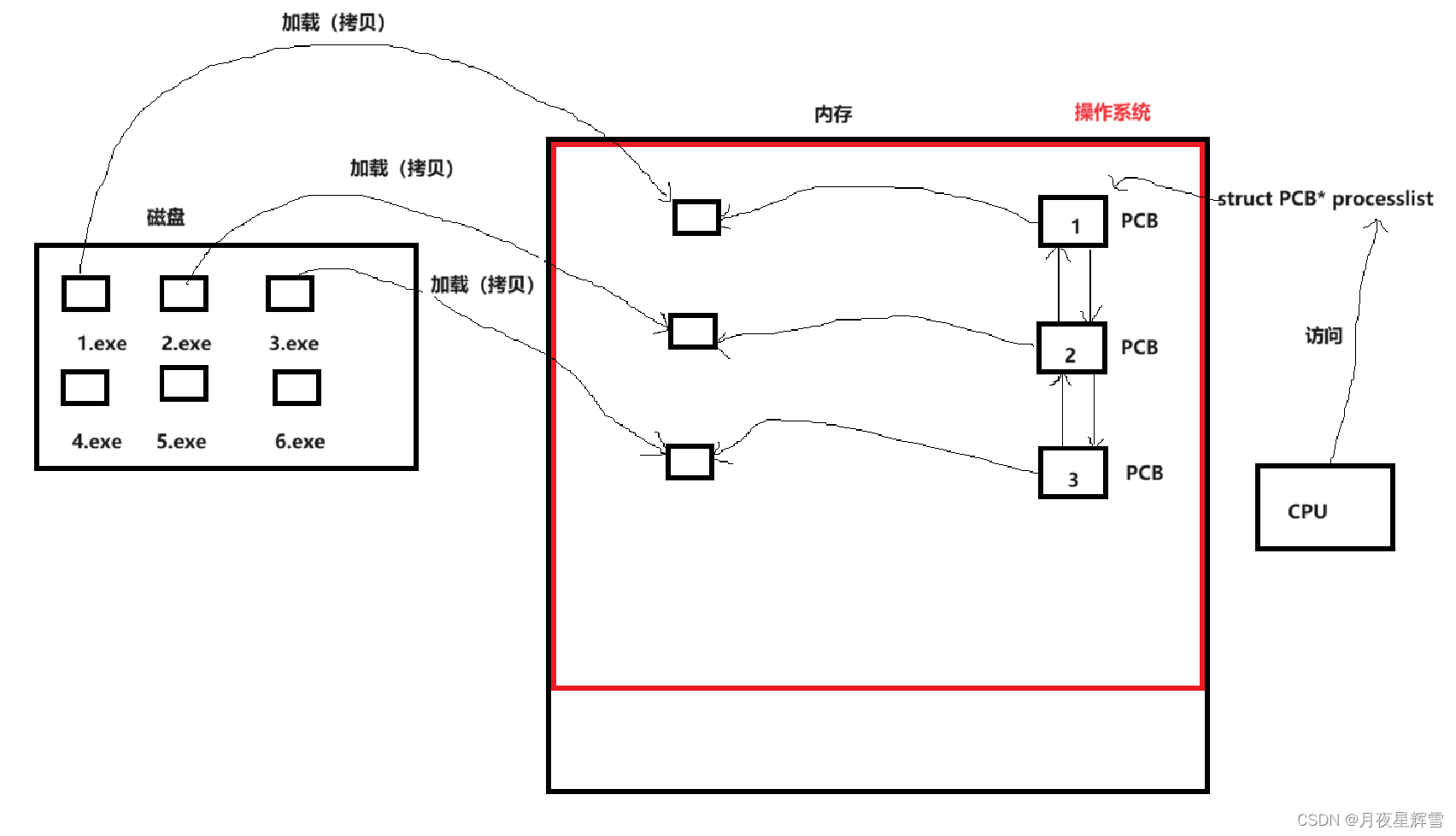
【进程管理】初识进程
一.何为进程 教材一般会给出这样的答案: 运行起来的程序 或者 内存中的程序 这样说太抽象了,那我问程序和进程有什么区别呢?诶?这我知道,书上说,动态的叫进程,静态的叫程序。那么静态和动态又是什么意思…...

ArcGIS Maps SDK for JS:监听按钮点击事件控制图层的visible属性
文章目录 1 需求描述2 解决方案 1 需求描述 现在有这么一个需求:在地图中添加一些图层,添加图层列表按钮。打开图层列表后用户会打开某些图层使其可见,要求关闭图层列表时,隐藏某些图层(若visibletrue) 2…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
