【PAT甲级题解记录】1007 Maximum Subsequence Sum (25 分)
【PAT甲级题解记录】1007 Maximum Subsequence Sum (25 分)
前言
Problem:1007 Maximum Subsequence Sum (25 分)
Tags:DP
Difficulty:
剧情模式想流点汗想流点血死而无憾Address:1007 Maximum Subsequence Sum (25 分)
问题描述
求最大连续子序列和,输出这个连续子序列的首值、尾值和序列和(优先最靠前的),如果都为这个序列都为负的输出0和整个序列的首尾值。
解题思路
- 一道经典又特殊的动态规划,本身很简单,但考虑到要求最靠前的首尾值,容易出错,难度相应提高。
- dp[i]dp[i]dp[i] 表示以 N[i]N[i]N[i] 为结尾的最大连续子序列和,再用一个 pos[i]pos[i]pos[i] 表示这个子序列的首位置。
- 优化:由于dp访问的单调性,可以压缩空间,用一个dp值和pos值代替这俩个数组。
参考代码
1. 未压缩空间:
#include<iostream>
#include<vector>using namespace std;
int K; // K integers 1e4
vector<int> N;
vector<int> dp, start_index;
int maxi;void init() {cin >> K;N.resize(K, 0);dp.resize(K, 0);start_index.resize(K, 0);for (int i = 0; i < K; ++i) {cin >> N[i];}}void do_dp() {maxi = 0;dp[0] = N[0];start_index[0] = 0;for (int i = 1; i < K; i++) {if (dp[i - 1] >= 0) {dp[i] = dp[i - 1] + N[i];start_index[i] = start_index[i - 1];} else {dp[i] = N[i];start_index[i] = i;}maxi = dp[i] > dp[maxi] ? i : maxi;}
}void solution_1007() {init();do_dp();if (dp[maxi] < 0) {cout << 0 << " " << N[0] << " " << N[K - 1] << endl;return;}cout << dp[maxi] << " " << N[start_index[maxi]] << " " << N[maxi] << endl;
}
int main() {solution_1007();return 0;
}2. 压缩空间:
(参考柳神 https://github.com/liuchuo/PAT/tree/master/AdvancedLevel_C++ )
这么写后竟然奇妙的发现当所有值都是负的时 leftindex 、rightindex会保持初始值,总而言之精简了很多,膜拜 orz。
#include<iostream>
#include<vector>using namespace std;
int K; // K integers 1e4
vector<int> N;
int dp, temp_start_index, left_index, right_index;
int maxx;void init() {cin >> K;N.resize(K, 0);for (int i = 0; i < K; ++i) {cin >> N[i];}}
void do_dp() {maxx = -1;dp = 0;temp_start_index = 0;left_index = 0;right_index = K - 1;for (int i = 0; i < K; i++) {// 注意从上一个循环继承来的 dp 值永远不会小于0,给原 dp 值加上 N[i] 后再判断dp = dp + N[i];if (dp < 0) { // 加上 N[i] 后 dp 小于0了,只可能因为 N[i] 为负数dp = 0;temp_start_index = i + 1;} else if (dp > maxx) { // 获得更大子串和maxx = dp;left_index = temp_start_index;right_index = i;}}
}void solution_1007() {init();do_dp();if (maxx < 0) {maxx = 0;}cout << maxx << " " << N[left_index] << " " << N[right_index] << endl;
}
int main() {solution_1007();return 0;
}总结
对于这种会保存下标的题,coding时不要分心写错了,一开始把 pos_start[i] = i 写成了 pos_start[i] = N[i],由于样例能过检查了好久才找出来(情人节不适合code)。
相关文章:
)
【PAT甲级题解记录】1007 Maximum Subsequence Sum (25 分)
【PAT甲级题解记录】1007 Maximum Subsequence Sum (25 分) 前言 Problem:1007 Maximum Subsequence Sum (25 分) Tags:DP Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1007 Maximum Subsequence Sum (25 分) 问题描…...
)
华为OD机试真题Python实现【 最小叶子节点】真题+解题思路+代码(20222023)
最小叶子节点 题目 二叉树也可以用数组来存储, 给定一个数组,树的根节点的值储存在下标1, 对于储存在下标n的节点,他的左子节点和右子节点分别储存在下标2*n和2*n+1, 并且我们用-1代表一个节点为空, 给定一个数组存储的二叉树, 试求从根节点到最小的叶子节点的路径, …...

mars3d动态轨迹DynamicRoamLine,如何获取实时运⾏的经纬度
问题 1.期望 实现 实时显示经纬度、⾼度,做电⼦围栏报警判断 2.第⼀步就是要,获取实时运⾏的经纬度信息、⾼度信息,然后通过算法做电⼦围栏判断 3.使⽤了参数getOverPositions,发现返回的不是经纬度 相关链接 http://mars3d.cn//e…...
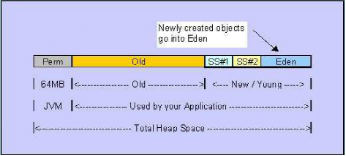
jvm常识
Jvm工作原理学习笔记0126一、JVM的生命周期1.JVM实例对应了一个独立运行的java程序它是进程级别a)启动。启动一个Java程序时,一个JVM实例就产生了,任何一个拥有public static void main(String[] args)函数的class都可以作为JVM实例运行的起点b)运行。ma…...
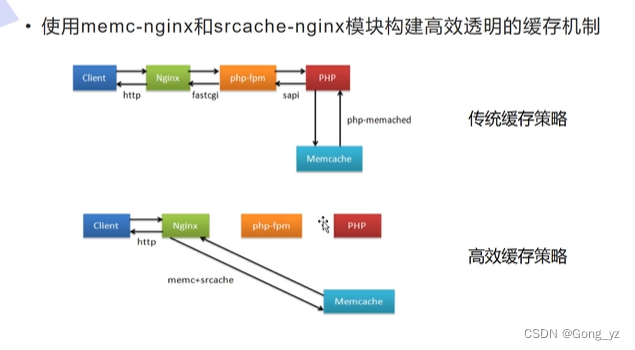
PHP部署、nginx与PHP的整合、PHP动态添加模块
文章目录前言一、基本知识1.php介绍2.PHP能做什么3.web工作原理4.PHP脚本主要用于领域5.php其他相关信息6.memcache介绍二、php的源码安装1.php安装2.php配置三、nginx与php整合四、php动态扩展模块(memcache模块)前言 一、基本知识 1.php介绍 官方下载…...

SpringCloud与SpringBoot的版本对应
一、SpringCloud与SpringBoot的版本对应 SpringCloud版本 SpringBoot版本 2021.0.1-SNAPSHOT Spring Boot >2.6.4-SNAPSHOT and <2.7.0-M1 2021.0.0 Spring Boot >2.6.1 and <2.6.4-SNAPSHOT 2021.0.0-RC1 Spring Boot >2.6.0-RC1 and <2.6.1 2021.0.0-M3 Sp…...

华为OD机试题,用 Java 解【N 进制减法】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

Linux->进程概念于基本创建
1. 进程基本概念 当一个可执行程序被加载到内存当中,并由操作系统将其管理起来,此时这个程序就被称之为进程。也就是下方的: 程序的一个执行实例,正在执行的程序等 担当分配系统资源(CPU时间,内存ÿ…...

【MySQL】5.7版本解压安装配置
前言 之所以使用解压版本,而不使用exe安装,因为exe的安装方式删除过于麻烦!!! 如果安装MySQL过程中,出错了或者想重新在来一把,删除mysql服务即可 sc delete mysql # 删除已经安装好的Mysql&a…...

c++类对象数据成员和虚函数的内存布局
一直想搞清楚类对象的数据成员和虚函数的内存布局,今天刚好有时间,所以就写了个demo查看了一下具体的内存布局情况(使用的编译器为微软的)。下面是自己demo的代码:#include <iostream> #include <windows.h&g…...
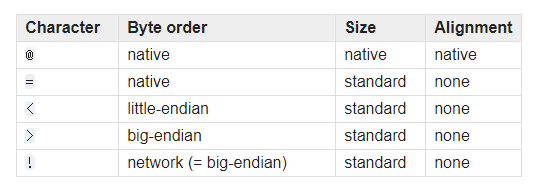
Python 模块和包
1. 模块和包 **容器:**列表、元组、字符串、字典等,对数据的封装**函数:**对语句的封装**类:**对方法和属性的封装,即对函数和数据的封装 而模块(module)就是个程序,一个.py 文件&…...

Java零基础专栏——面向对象
1 面向对象思想1.1 什么是面向对象?2 类和对象2.1 类和对象的理解2.2 类的定义2.3定义类的补充注意事项2.4 对象的使用2.5 练习3 封装3.1 封装思想3.1.1 封装概述3.1.2 封装的步骤3.1.3 封装代码实现3.2 private关键字3.3 练习—private的使用4 构造方法4.1 构造方法…...

离散无记忆与有记忆信源的序列熵
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录离散无记忆信源的…...
算法该不该刷?如何高效刷算法?
一、算法该不该刷?最近有小伙伴向我咨询一个问题,就是算法该不该刷,该如何刷算法呢?这个问题可谓太大众化了,只要你去某乎、某度搜索一下相关的解答,会有无数种回答,可见这个问题困扰了多少学习…...
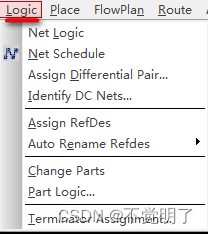
Allegro如何在关闭飞线模式下查看网络连接位置操作指导
Allegro如何在关闭飞线模式下查看网络连接位置操作指导 在用Allegro做PCB设计的时候,有时会因为设计需要,关闭飞线显示。 如何在关闭飞线显示模式下查看网络连接的位置,如下图 除了能看到网络连接的点位以外,还能看到器件的pin Number 如何显示出这种效果,具体操作如下 …...
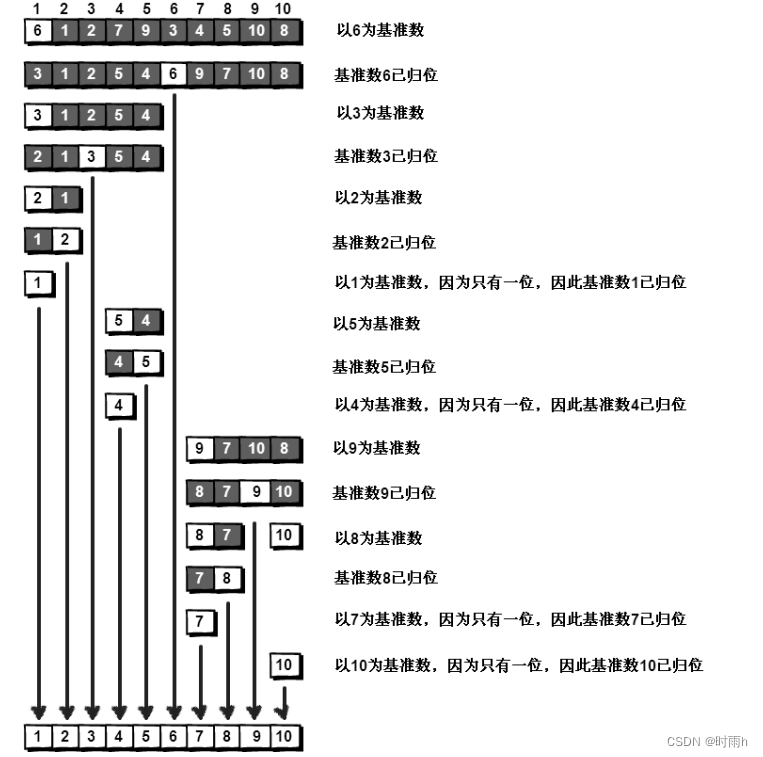
啊哈 算法读书笔记 第 1 章 一大波数正在靠近——排序
目录 排序算法: 时间复杂度: 排序算法和冒泡排序之间的过渡: 冒泡排序 冒泡排序和快速排序之间的过渡: 快速排序 排序算法: 首先出场的是我们的主人公小哼,上面这个可爱的娃就是啦。期末考试完了老…...
:HTTP请求与响应)
Servlet笔记(5):HTTP请求与响应
1、HTTP请求 当浏览器请求网页时,它会向Web服务器发送特定信息,这些信息不能被直接读取,而是通过传输HTTP请求时,封装进请求头中。 有哪些头信息? 头信息描述Accept这个头信息指定浏览器或其他客户端可以处理的 MIME…...
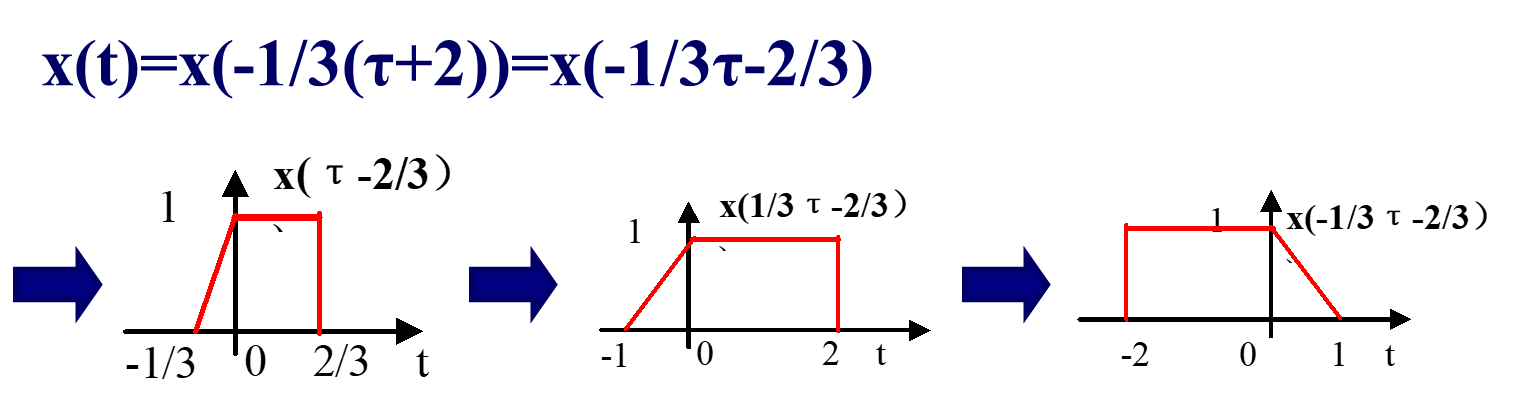
信号的运算与变换
目录 前言 本章内容介绍 信号的运算与变换 相加 相乘 时移 反折 尺度变换 微分(差分) 积分(累加) 信号的奇偶求解 信号的实虚分解 合适的例题 1、时移反折 2、时移尺度 3、时移反折尺度 4、反求x(t) 前言 《信号…...

【GO】K8s 管理系统项目9[API部分--Secret]
K8s 管理系统项目[API部分–Secret] 1. 接口实现 service/dataselector.go // secret type secretCell corev1.Secretfunc (s secretCell) GetCreation() time.Time {return s.CreationTimestamp.Time }func (s secretCell) GetName() string {return s.Name }2. Secret功能…...
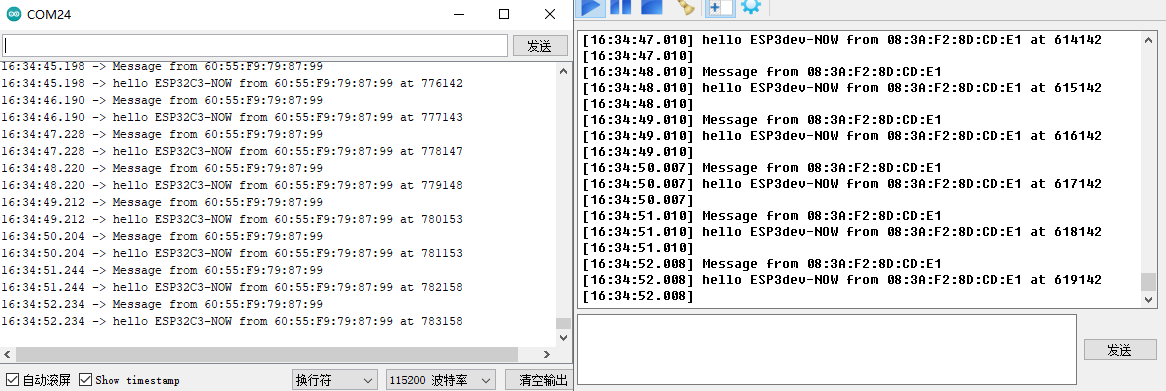
ESP32 Arduino EspNow点对点双向通讯
ESP32 Arduino EspNow点对点双向通讯✨本案例分别采用esp32和esp32C3之间点对点单播无线通讯方式。 🌿esp32开发板 🌾esp32c3开发板 🔧所需库(需要自行导入到Arduino IDE library文件夹中,无法在IDE 管理库界面搜索下载到该库)&am…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
