电路原理解题笔记(一)
文章目录
- 贼基础的知识
- 等效电阻
- 基尔霍夫电流定律
- 电阻电路的一般分析
- 支路电流法
- 节点电压法
- 回路电流法
- 电路定理
- 叠加定理
- 戴维宁等效电路
- 诺顿等效电路
- 求某电阻值为多少可吸收最大功率。
- 吸收、释放功率
第一个月,对应猴博士的一到五课时。
- 贼基础的知识
- 电阻电路的等效变换
- 基尔霍夫定律
- 电阻电路的一般分析
- 电路定理
贼基础的知识
虽然这部分是听过的,但是为了使得笔记与知识体系的完整,还是应该快速过一边吧。
讲解串联并联、以及常见概念。
然后讲解电压源,大学的电压源。以及讲解电流源。
以及讲解了电压源与电流源和电阻串并联等效的情况。
然后讲了电位、电位差,等电位的情况。
说法不少,但是就是要抓住做法背后的原理。
等效电阻
- 电压源串联可合并
- 电流源并联可合并
- 电压源电流源串联,省略电压源
- 电压源电流源并联,省略电流源
- 电压源转化为电流源
- 电流源转化为电压源
前面的还是挺好理解的,后面两个注意方向。本质上来说还是直观的。
可能还是需要专门了解一下戴维南、诺顿吧。不过先把题会做再从题目中认识也是可以的。
然后给出了例题。
感受:有并联先并联。主要还是看标准的等效电路图,拿不准不要直接用。
变换没什么问题,那么主要在什么情况下应该怎么处理就成了关键问题。
根据观察和猴的总结,可以得出结论:
- 最终的目的是串联电路
- 并联电路可以合并为更少的并联电路。如果由于既有电压源又有电阻合并不了,那么就应该变换了。
- 串联电路可以合并为元件更少的串联电路。
- 多可能只是说暂时的,为的是更好地等效,就如上述第二点一样。
- Δ − Y \Delta - Y Δ−Y 等效变换
其实这个反而是最不需要说的,肉眼可见的需要记忆。不过还是用latex描述一遍吧。
不对,用latex描述其实不如使用文字描述。这样更有助于记忆。
Δ 变 Y : \Delta 变 Y: Δ变Y:
Y 形电阻 = Δ 形相邻电阻乘积 Δ 形电阻之和 Y形电阻 = \frac{\Delta形相邻电阻乘积}{\Delta形电阻之和} Y形电阻=Δ形电阻之和Δ形相邻电阻乘积
Y 变 Δ : Y 变 \Delta: Y变Δ:
Δ 形电阻 = Y 形电阻两两乘积之和 Y 形不相邻电阻 \Delta形电阻 = \frac{Y形电阻两两乘积之和}{Y形不相邻电阻} Δ形电阻=Y形不相邻电阻Y形电阻两两乘积之和
基尔霍夫电流定律
节点流入等于流出。
任意回路电压降为零。
其实就是麦克斯为方程的忽略了一些因素下的产物。
对于选取节点和回路的问题,就是那里已知条件多,就直接往上莽就行了。
电阻电路的一般分析
先介绍了什么是支路、回路、节点、网孔这些概念。
支路电流法
- 找出结点数,并选择任意(节点数-1)个节点列电流方程
- 找出支路数,选(支路数-节点数+1)个回路,列电压方程
- 联立上面的方程,带入数值,解方程。
最终结果是电流
节点电压法
- 找出所有节点,选择与带球向相关的一个结点表上数字0,给其他节点分别标记为数字1,2,3……
- 将与电流源串联的电阻变到先,与电压源并联的电阻变短路,让G11等于节点一各支路的电阻的倒数和,以此类推,找出节点二的G22、节点三的G33
- 找出连接节点1、2支路的电阻,并让G21=G12=1、2连接支路上阻值的负倒数。
- 找出节点一支路上的电压源或电流源,并让is11=电压源/所在支路电阻+电流源产生电流(流入节点为正,流出节点为负),以此类推找出is22、is33.
然后上面终于把准备工作做完了,列方程
列的就是G的矩阵乘以un几=is11、22、33.
算出来的就是每个节点的电压
回路电流法
- 找出支路数、节点数、选取(支路数-节点数+1)个回路,并指定回路电流绕行方向
- 另r11=回路一电阻之和,r22……
- r12=r21=回路1、2共有电阻:与指定回路电流绕行方向相同就是正,相反就是负
- 令us1=回路一中所有电压源之和、令us2=回路二中所有电流源之和。
- 对每个回路列方程,就是和上面节点电压法差不多的,电阻的矩阵乘以i1、2、3等于u11、22、33.
求得的是各个回路电流。
我需要记得每种方法最后得到的方程是啥样的,从而知道每种方法需要的准备工作是什么。
电路定理
叠加定理
- 求出出待求部分,让部分内的电压源变导线、电流源断开、求出待求内容。
这里有一些需要对电路进行等效变换的部分,练出来的吧。 - 恢复待求部分,让部分外的电压源变导线,电流源断开,求出待求内容
- 第一步的结果加上第二步的结果。
就是先把待求部分里面的变换了求了,在把待求部分外的变换了求了。
戴维宁等效电路
- 求开路电压uoc。
- 在开路处接上一个独立电压源us,令原电路电压源变导线,电流源变短路,求出六经us的电流is,求出req
- 然后就等效为一个uoc串联一个req
诺顿等效电路
- 连接开路,求isc(就是上面的开路变成短路)
- 同上,就是为了req
- 然后等效为一个isc并联一个req
求某电阻值为多少可吸收最大功率。
- 简单来说,把这个电阻拿出来,其余部分戴维宁等效
- 电阻等于req时吸收最大,高中知识。
吸收、释放功率
这个和前面到是没什么区别,相当于就是说是扩展了电源的吸收释放的问题
电流从高电压流向低电压则吸收功率,反之则释放功率。
相关文章:
)
电路原理解题笔记(一)
文章目录 贼基础的知识等效电阻基尔霍夫电流定律电阻电路的一般分析支路电流法节点电压法回路电流法 电路定理叠加定理戴维宁等效电路诺顿等效电路求某电阻值为多少可吸收最大功率。吸收、释放功率 第一个月,对应猴博士的一到五课时。 贼基础的知识电阻电路的等效变…...
分享几个优秀开源免费管理后台模版,建议收藏!
大家好,我是 jonssonyan 今天和大家分享一些免费开源的后台管理页面,帮助大家快速搭建前端页面。为什么要用模板?道理很简单,原因是方便我们快速开发。我们不应该花太多的时间在页面调整上,而应该把精力放在核心逻辑和…...

BFS模板:844. 走迷宫
给定一个 nmnm 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。 最初,有一个人位于左上角 (1,1)(1,1) 处,已知该人每次可以向上、下、左、右任意…...
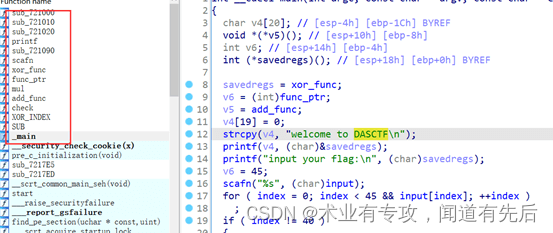
re学习(37)DASCTF 2023 0X401七月暑期挑战赛 controflow
程序通过改变栈里面的返回地址来控制程序的控制流 从而达到混淆的效果 左侧有许多被hook的函数 在每个函数开头设置断点 然后观察程序的运行流程 会发现输入的数据会进行 异或 相加 异或 相减 相乘 异或等操作 要注意部分运算的索引是 从[10]开始的 具体思路参考…...
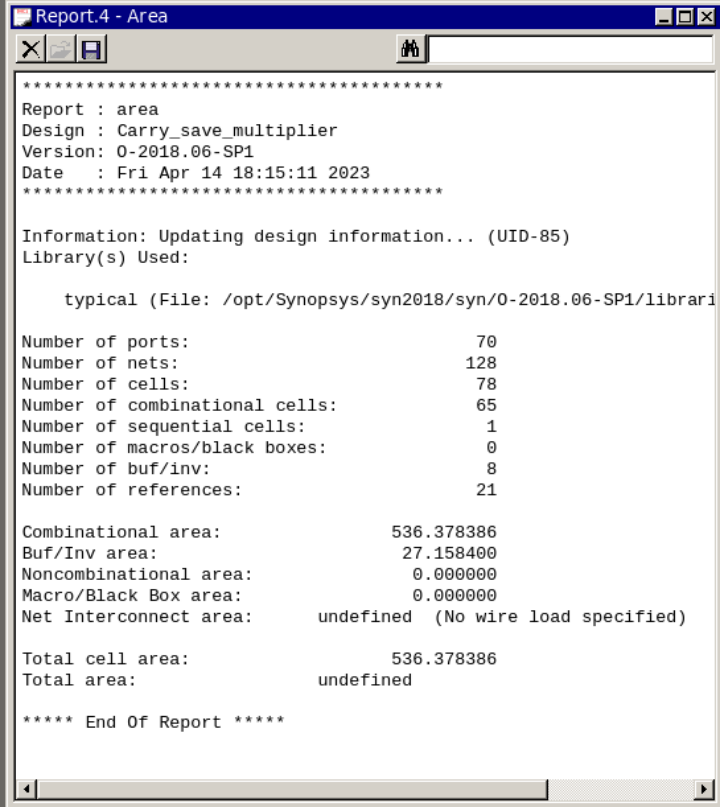
数字IC前端学习笔记:数字乘法器的优化设计(进位保留乘法器)
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 阵列乘法器设计中限制乘法器速度的是随着数据位宽而迅速增大的串行进位链,如果使用进位保留加法器,则可以避免在设计中引入较长时间的等待&…...

prority_queue的学习
优先级队列(Priority Queue)是一种抽象数据类型,它类似于普通的队列或堆栈,但每个元素都有一个关联的优先级,这个优先级决定了元素在队列中的位置和被访问的顺序。在优先级队列中,具有最高优先级的元素通常…...
【vue3】toRef与toRefs的使用,toRef与ref的区别
假期第四篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 1、toRef与toRefs 创建一个ref对象,其value值指向另一个对象中的某个属性 语法:const name toRef(person,‘name’…...

信息论基础第二章部分习题
2.5 证明若H(Y|X)0,则Y是X的函数 若 H ( Y ∣ X ) 0 H(Y|X) 0 H(Y∣X)0,意味着在已知 X X X 的条件下, Y Y Y 的不确定性为零,即给定 X X X 的值,我们完全确定了 Y Y Y 的值。这表明 Y Y Y 的取值完全由 X X…...

信息化发展73
数字经济 数字经济是继农业经济、工业经济之后的更高级经济形态。从本质上看,数字经济是一种新的技术经济范式,它建立在信息与通信技术的重大突破的基础上,以数字技术与实体经济融合驱动的产业梯次转型和经济创新发展的主引擎,在…...

560. 和为 K 的子数组
题目描述 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 输出:2…...
24 mysql all 查询
前言 这里主要是 探究一下 explain $sql 中各个 type 诸如 const, ref, range, index, all 的查询的影响, 以及一个初步的效率的判断 这里会调试源码来看一下 各个类型的查询 需要 lookUp 的记录 以及 相关的差异 此系列文章建议从 mysql const 查询 开始看 测试表结构…...

【Excel单元格数值统计】python实现-附ChatGPT解析
1.题目 Excel单元格数值统计 知识点: 递归、循环数组 时间限制:2s 空间限制:256MB 限定语言:不限 题目描述: Excel工作表中对选定区域的数值进行统计的功能非常实用。仿照Excel的这个功能,请对给定表格中选中区域中的单元格进行求和统计,并输出统计结果。 为简化计算,假设当…...

爬虫项目实战——爬取B站视频
目标:对B站视频详情页url进行视频的爬取。 注:由于B站的音频和视频的链接是分开的,所以在提取是需要分别提取,然后进行合成。 这里只管提取,合成的工作以后再说。 具体步骤 发送请求 对于视频详情页url地址发送请求 …...
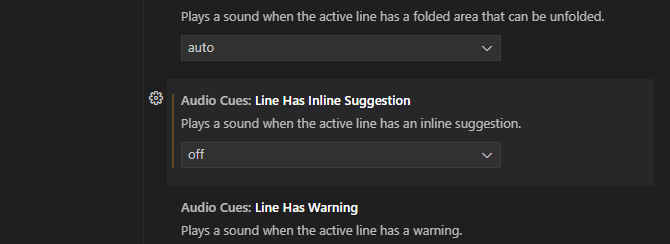
关掉在vscode使用copilot时的提示音
1. 按照图示的操作File --> Preferences --> Settings 2. 搜索框输入关键字Sound,因为是要关掉声音,所以找有关声音的设置 3. 找到如下图所示的选项 Audio Cues:Line Has Inline Suggetion,将其设置为Off 这样,就可以关掉suggest code时…...

【有限域除法】二元多项式除法电路原理及C语言实现
二元多项式除法电路原理 例: g ( x ) = x 4 + x 2 + x + 1 g(x)=x^4 + x^2+x+1...
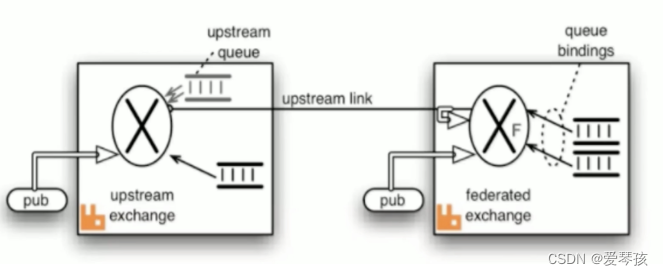
RabbitMQ核心总结
AMQP协议核心概念 RabbitMQ是基于AMQP协议的,通过使用通用协议就可以做到在不同语言之间传递。 server:又称broker,接受客户端连接,实现AMQP实体服务。 connection:连接和具体broker网络连接。 channel:…...
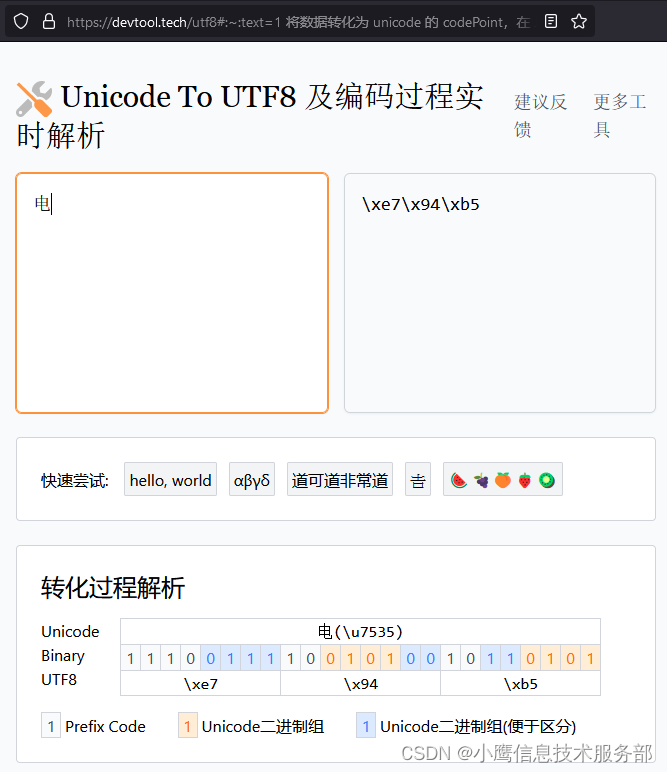
Unicode与UTF-8
软件开发中乱码问题经常遇到,Unicode,UTF-8, ASCII等都是高频词语,不过具体是啥意思其实都不清楚。这个周末研究了一下,略有了解,记录一下。 Unicode Unicode本身是纯理论的东西,和具体计算机实现无关。它…...

A : DS单链表--类实现
Description 用C语言和类实现单链表,含头结点 属性包括:data数据域、next指针域 操作包括:插入、删除、查找 注意:单链表不是数组,所以位置从1开始对应首结点,头结点不放数据 类定义参考 #include<…...

React Hooks —— ref hooks
什么是Hooks Hooks从语法上来说是一些函数。这些函数可以用于在函数组件中引入状态管理和生命周期方法。 React Hooks的优点 简洁 从语法上来说,写的代码少了上手非常简单 基于函数式编程理念,只需要掌握一些JavaScript基础知识与生命周期相关的知识不…...

泛型与Gson解析
/*** 回调接口的一种实现* 用于把网络返回的json字符串转换成参数化类型* 泛型 T 就是用户输入的javaBean的类型*/ public abstract class HttpCallback<T> implements ICallback {Overridepublic void onSuccess (String result) {// result就是网络回来的数据// 把这个…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
