Pyhon-每日一练(1)

🌈write in front🌈
🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页:Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:Aileen_0v0🧸的PYTHON学习系列专栏——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马~"

目录
(1)两数求和
(2)找100以内的偶数
(3)找出 100 以内的奇数
(4) 判断素数(质数)
(1)两数求和
# (1)两数求和
num1 = 1
num2 = 2
result = num1 + num2
print(result)
#3(2)找100以内的偶数
#(2)找出 100 以内的偶数
# tip1:
for i in range (0,100):if i % 2 == 0:print(i)偶数数目较多,如果我不想每次判断完,再输出,我们应该如何修改这个代码?
# tip2:
list = []
for i in range (0,100):if i % 2 == 0:list.append(i)
print(list)#[0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98](3)找出 100 以内的奇数
#(2)找出 100 以内的奇数
# tip 1:
list = []
for i in range(0,100):if i % 2 != 0 :list.append(i)
print(list)
#tip 2:
list2 = []
for i in range(1,100,2):list2.append(i)
print(list2)(4) 判断素数(质数)
编写程序,判断某一个数是否为素数。所谓素数指的是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。(1不是素数)
#判断素数
#tip 1:
n = int (input("请输入一个正整数:"))
if n <=1:flag = True
else:flag = False
for i in range (2,n):if n % i == 0 :flag = Truebreak
if flag:print(f"{n}是合数")
else:print(f"{n}是素数")根据上面的代码验证一个数是否为素数,一般做法要把小于他的数全试一遍,比较麻烦。
不过现在只需要试几个素数就可以了。
筛法就是这样的原理
例如:求100内的素数,只需2,3,5,7这几个素数,将他们的倍数一一划入,剩下的就是待求的素数了。也就是说,一个小于100的数只要不是2357的倍数,就一定是素数。
如果是1000内的素数,就需要划入从2到31的素数的倍数。
考虑这个最大的素数是怎么给出的。
7和11是相邻的素数7*7=49_11*11=121
100就在他们之间。所以最大的素数就是7。
还可以给出更强的结论,求120内的素数依然可以仅使用2357
1000内的可以同样推得。
按照这样的想法,要判断一个数是否为素数,可以划分根据素数的平方来划定区间边界。
看他落在哪个区间。
2*2=43*3=9
5*5=25
7*7=49
11*11=121
...
尝试一下,比如57--->57**0.5 = 7.54
位于49-121区间,考虑235757/2=28...1
57/3=19
57/5=11...2
57/7=8...1
被3整除,故为合数。
试试59--->59**0.5 = 7.68
位于49-121,同样考虑235759/2=29...1
59/3=19...2
59/5=11...4
59/7=8...3
不能整除,是素数
同样,很大的数也可以这样算。
因为他是按照素数平方划定边界的,所以可以迅速增长到很大的值。
虽然是很小的技巧,但很大的提高了计算和判断的速度.
#tip 2:
n = int(input("请输入一个正整数:"))
flag = True
if n <= 1:flag = False
else:for i in range(2, int(n**0.5)+1):if n % i == 0:flag = Falsebreakif flag:print(n, "是素数")
else:print(n, "不是素数")
相关文章:

Pyhon-每日一练(1)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...
MySQL:数据库的物理备份和恢复-冷备份(3)
介绍 物理备份: 直接复制数据文件进行的备份 优点:不需要其他的工具,直接复制就好,恢复直接复制备份文件即可 缺点:与存储引擎有关,跨平台能力较弱 逻辑备份: 从数据库中导出数据另存而进行的备…...

功能比较:Redisson vs Jedis
Redis最流行的两个Java客户端库是Redisson和Jedis。Redisson提供内存中的数据网格功能,支持Redis的各种分布式对象和服务。另一方面,Jedis是一个更轻量级的产品,它缺乏其他库的某些功能。 如果你正在为Redis寻找一个Java客户端库…...
Spring web security
儅使用spring的web security時,默認會轉向自帶的spring security example page。而不會轉向error page。 TODO: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-security</artifactId> &l…...
SpringCloud(二)Docker、Spring AMQP、ElasticSearch
文章目录 DockerDocker与虚拟机Docker架构镜像、容器、镜像托管平台Docker架构Docker实践 Spring AMQP简单使用案例工作队列- WorkQueue发布订阅服务FanoutExchangeDirectExchangeTopicExchange 消息转换器 ElasticSearch倒排索引IK分词器IK分词拓展与停用字典 操作索引库mappi…...
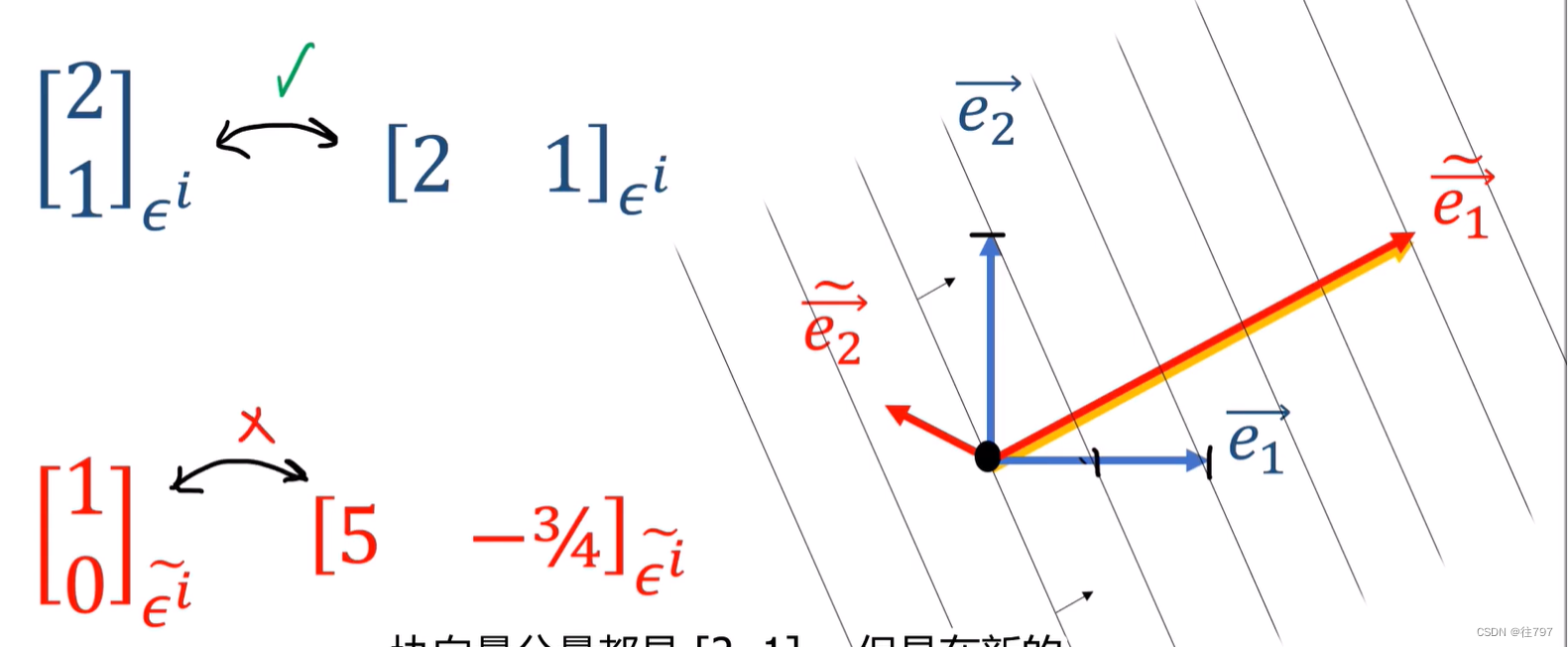
7.Tensors For Beginneers - Convector Components
介绍协向量时,曾说过它们有点像 行向量, 行向量确实以某种方式代表了协向量, 这里说明一下: 协向量是不变的; 协向量组件是可变的。 协向量不依赖坐标系,协向量的组件取决于坐标系。 当我们说协向量具有组…...

直线导轨坏了可以维修吗?
直线导轨是工业自动化设备中常用的零部件,其性能和使用寿命对设备的稳定运行和产能有着直接的影响,在生产中,由于各种原因,直线导轨会出现各种问题,那么,直线导轨的维修方法究竟是怎样的呢?我们…...

Java基础--泛型详解
一、背景 java推出泛型之前,集合元素类型可以是object类型,能够存储任意的数据类型对象,但是在使用过程中,如果不知道集合里面的各个元素的类型,在进行类型转换的时候就很容易引发ClassCastException异常。 二、概念 …...
学习搜狗的workflow,MacBook上如何编译
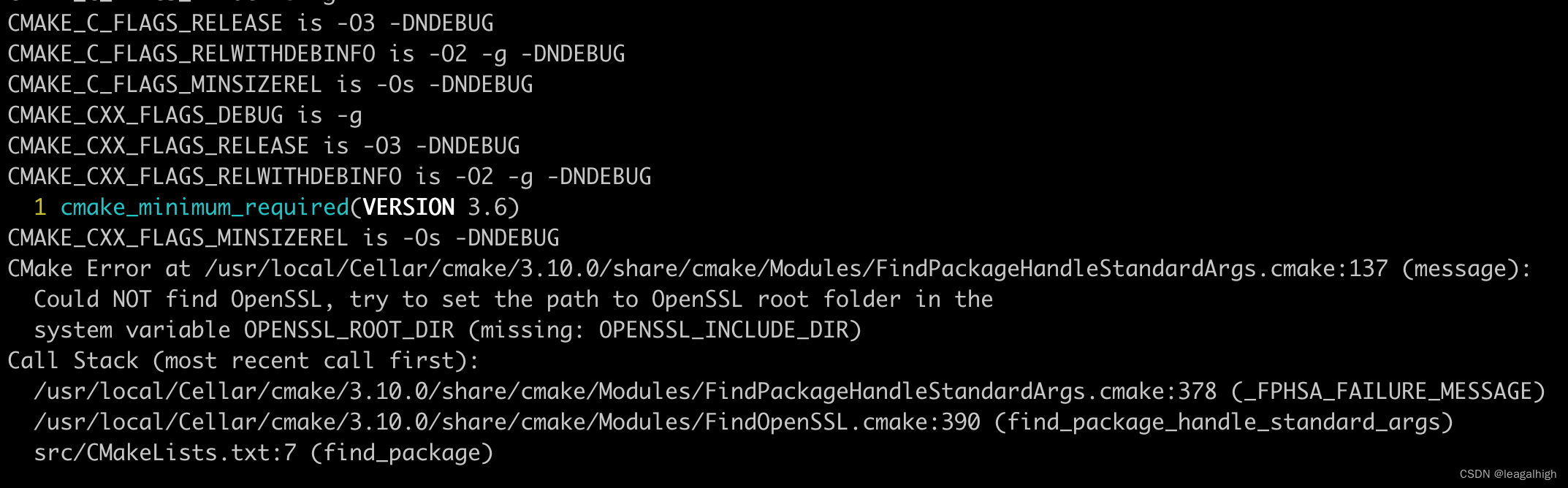
官网说可以在MacBook上也可以运行,但是编译的时候却有找不到openssl的错误: 看其他博客也有类似的错误,按照类似的思路去解决 问题原因和解决办法 cmake编译的时候,没有找到openssl的头文件,需要设置cmake编译环境下…...
Ubuntu使用cmake和vscode开发自己的项目,引用自己的头文件和openCV
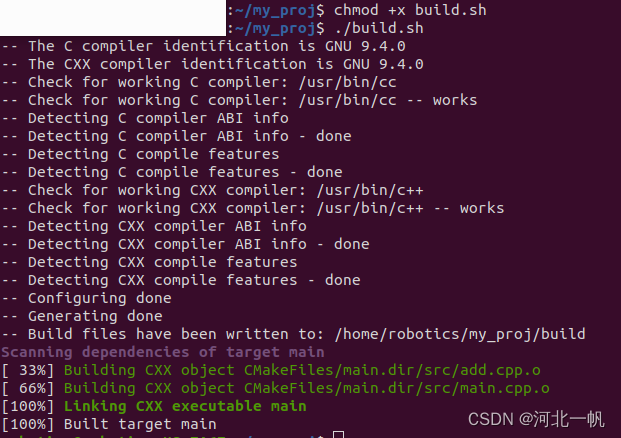
创建文件夹 mkdir my_proj 继续创建include 和 src文件夹,形成如下的目录结构 用vscode打开项目 创建add.h #ifndef ADD_H #define ADD_Hint add(int numA, int numB);#endif add.cpp #include "add.h"int add(int numA, int numB) {return numA nu…...
 dataset, dataloader)
2) dataset, dataloader
dataset, dataloader torchvision.datasets里面集成了一些常见的数据集,例如MNIST和CIFAR10 1) Dataset 以MNIST为例,其使用方式如下 import torch import torchvision from torchvision import transformstrain_dataset = torchvision.datasets.MNIST(root=../data,trai…...

阿里云PolarDB自研数据库详细介绍_兼容MySQL、PostgreSQL和Oracle语法
阿里云PolarDB数据库是阿里巴巴自研的关系型分布式云原生数据库,PolarDB兼容三种数据库引擎:MySQL、PostgreSQL、Oracle(语法兼容),目前提供云原生数据库PolarDB MySQL版、云原生数据库PolarDB PostgreSQL版和云原生数…...
[软件工具]opencv-svm快速训练助手教程解决opencv C++ SVM模型训练与分类实现任务支持C# python调用
opencv中已经提供了svm算法可以对图像实现多分类,使用svm算法对图像分类的任务多用于场景简单且对时间有要求的场景,因为opencv的svm训练一般只需要很短时间就可以完成训练任务。但是目前网上没有一个工具很好解决训练问题,大部分需要自己编程…...
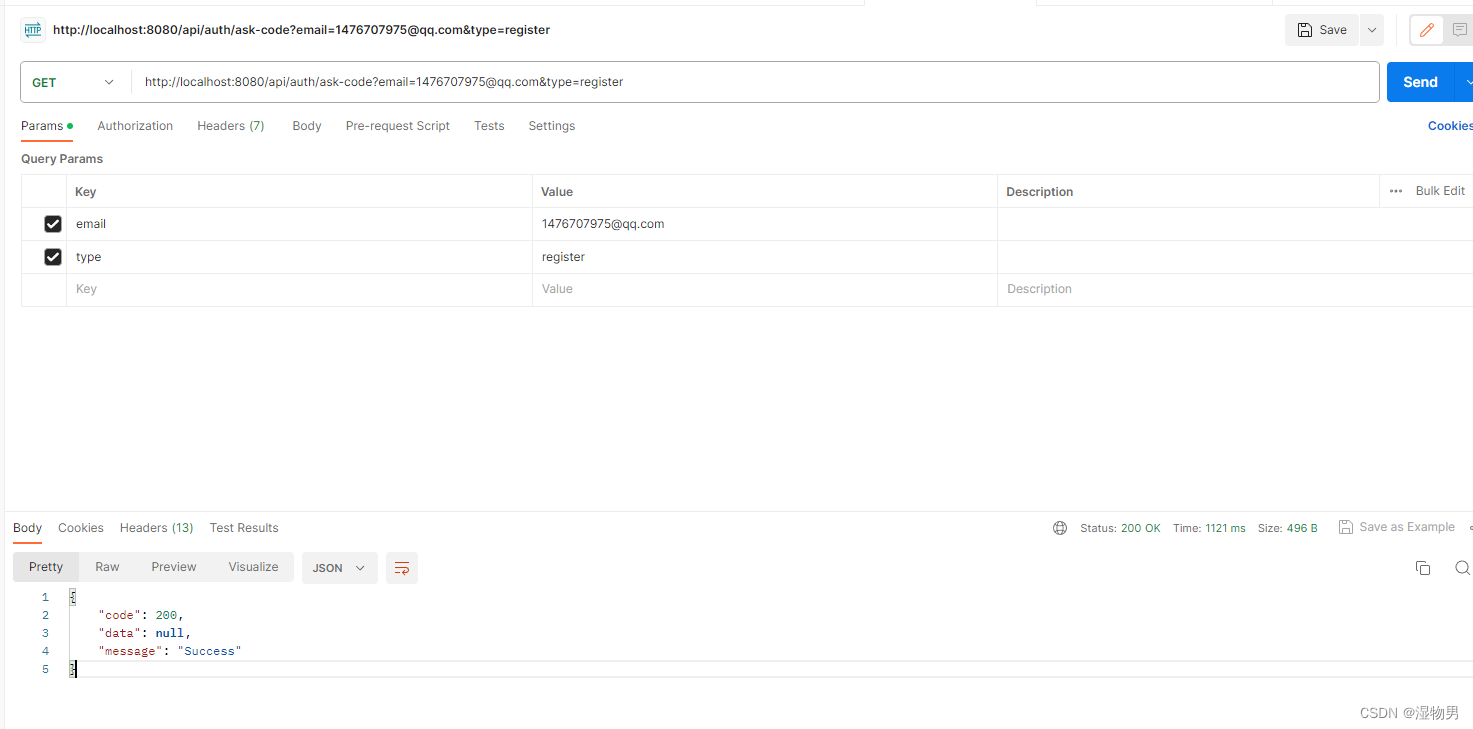
邮件注册(一)验证码发送
通过邮箱实现注册,用户请求验证码完成注册操作。 导入依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId></dependency><dependency><g…...
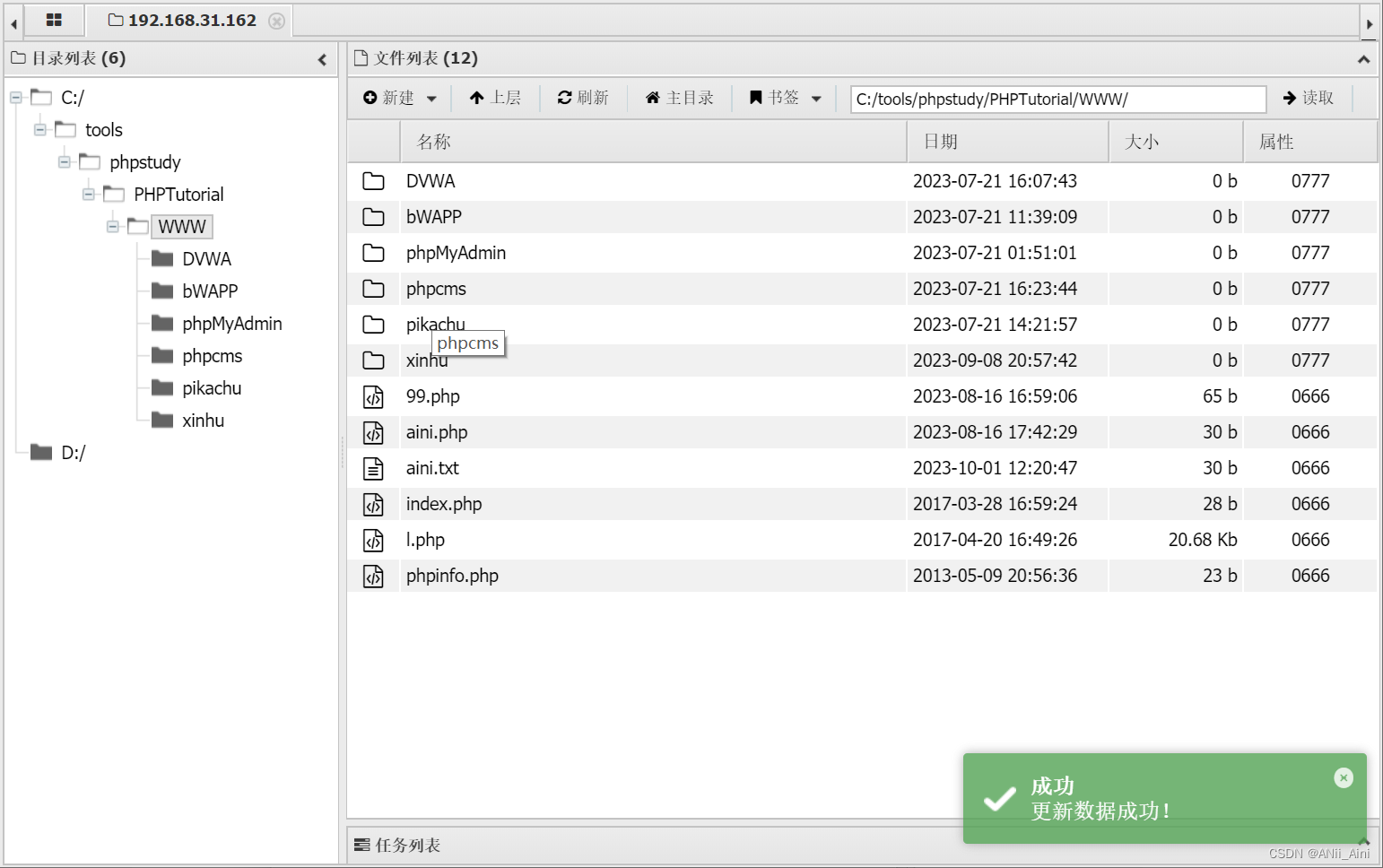
【网络安全---sql注入(2)】如何通过SQL注入getshell?如何通过SQL注入读取文件或者数据库数据?一篇文章告诉你过程和原理。
前言 本篇博客主要是通过piakchu靶场来讲解如何通过SQL注入漏洞来写入文件,读取文件。通过SQL输入来注入木马来getshell等,讲解了比较详细的过程; 如果想要学习SQL注入原理以及如何进行SQL注入,我也写了一篇详细的SQL注入方法及…...
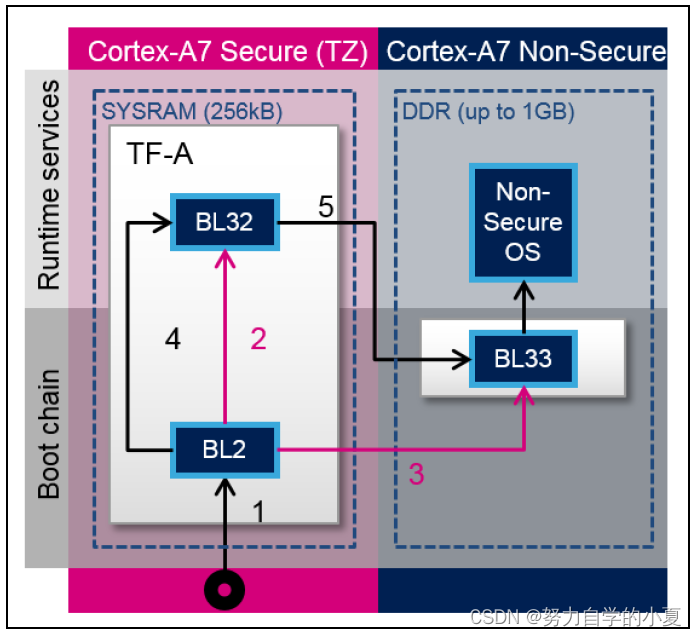
正点原子嵌入式linux驱动开发——TF-A移植
经过了之前的学习,除了TF-A的详细启动流程仍待更新,TF-A的使用和其对应的大致启动流程已经进行过了学习。但是当我们实际做产品时,硬件平台肯定会和ST官方的有区别,比如DDR容量会改变,自己的硬件没有使用到官方EVK开发…...
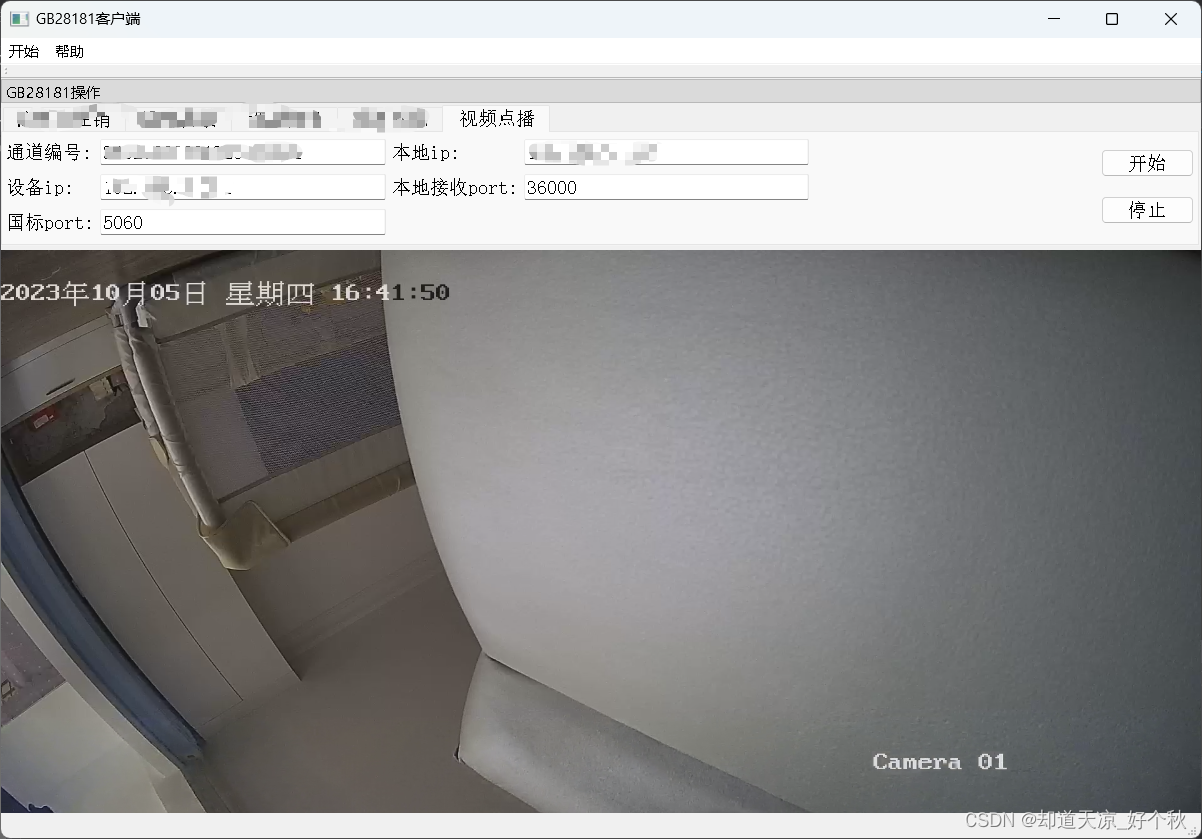
GB28181学习(六)——实时视音频点播(数据传输部分)
GB28181系列文章: 总述:https://blog.csdn.net/www_dong/article/details/132515446 注册与注销:https://blog.csdn.net/www_dong/article/details/132654525 心跳保活:https://blog.csdn.net/www_dong/article/details/132796…...
JMeter接口自动化测试(数据驱动)
之前我们的用例数据都是配置在HTTP请求中,每次需要增加,修改用例都需要打开JMeter重新编辑,当用例越来越多的时候,用例维护起来就越来越麻烦,有没有好的方法来解决这种情况呢?我们可以将用例的数据存放在cs…...

数据结构:二叉树(超详解析)
目录 1.树概念及结构 1.1树的概念 1.2树的相关概念 1.3树的表示 1.3.1孩子兄弟表示法: 1.3.2双亲表示法:只存储双亲的下标或指针 两节点不在同一树上: 2.二叉树概念及结构 2.1.概念 2.2.特殊的二叉树: 2…...

【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 4. 对坐标的曲面积分(第二类曲面积分)与场论初步
文章目录 二、曲面积分2.2 对坐标的曲面积分(第二类曲面积分)1. 问题产生 —— 流量2. 对坐标的曲面积分的定义(了解)3. 对坐标的曲面积分的性质4. 对坐标的曲面积分的计算法(1) 二重积分法(2&a…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
