7.Tensors For Beginneers - Convector Components
介绍协向量时,曾说过它们有点像 行向量, 行向量确实以某种方式代表了协向量,
这里说明一下:
协向量是不变的; 协向量组件是可变的。

协向量不依赖坐标系,协向量的组件取决于坐标系。
当我们说协向量具有组件时,我们的意思是?

要记住:协向量是 一个 从向量到实数的函数,协向量并不存在向量空间V中,协向量只是将V中的向量作为输入,所以我们不能使用V中的基向量来构造协向量,
所以应该怎么做才对?

从V中取两基向量,并引入两个协向量(从向量到实数的函数),
并定义它们的计算结果,
如图: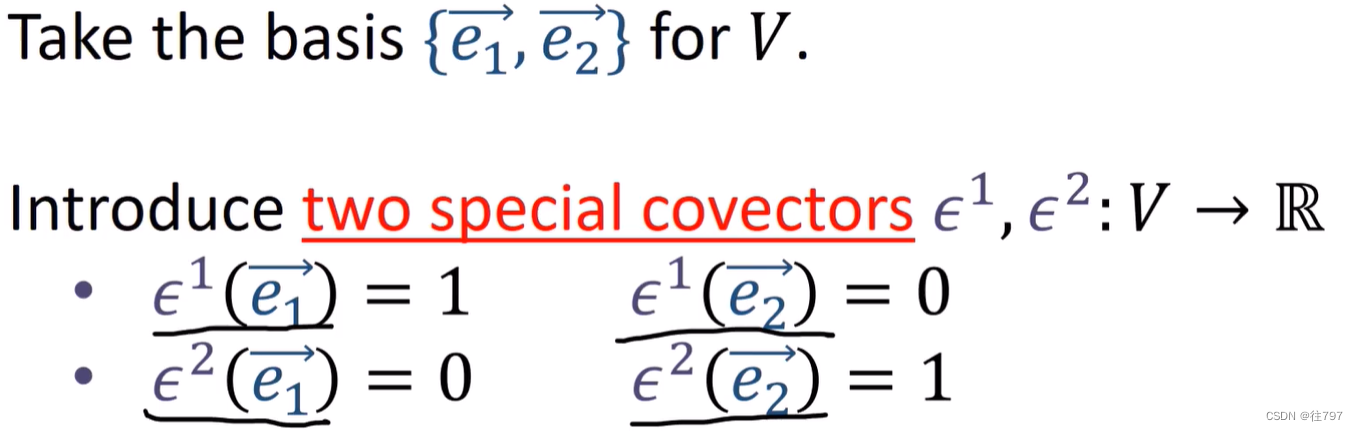
还记得那个 kronecker Delta 吗。
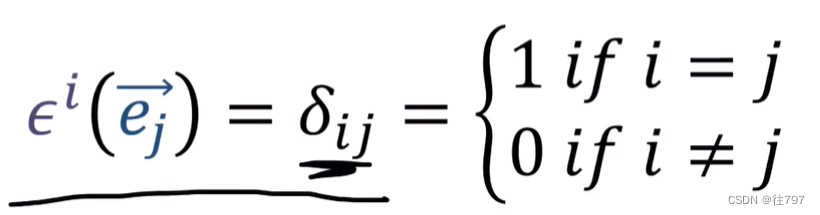
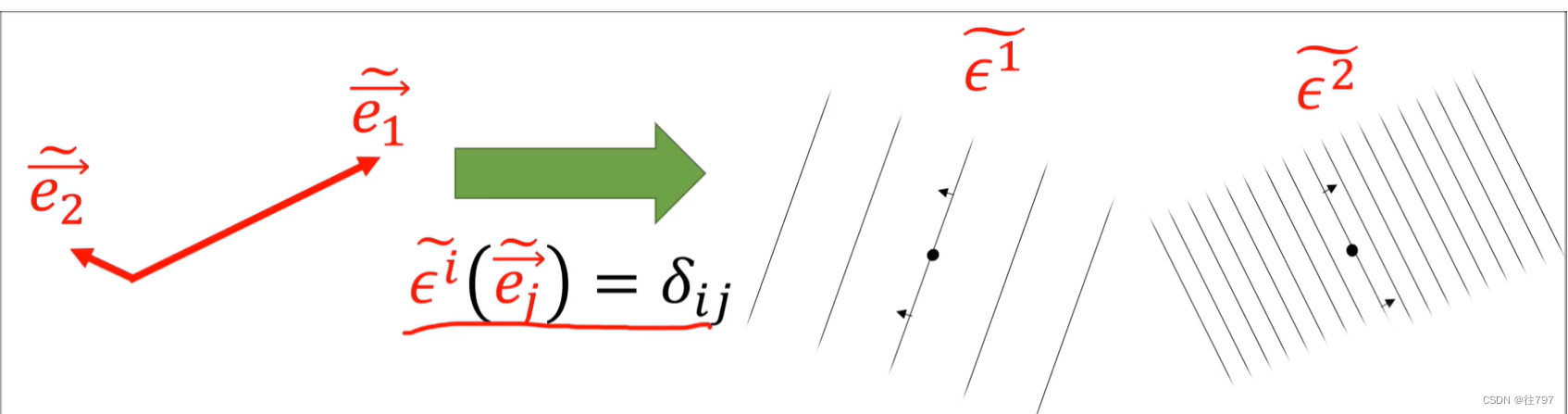
这些协向量 实际上看起来像一堆线吗? 为找到答案,把它们作用到某个向量v上,
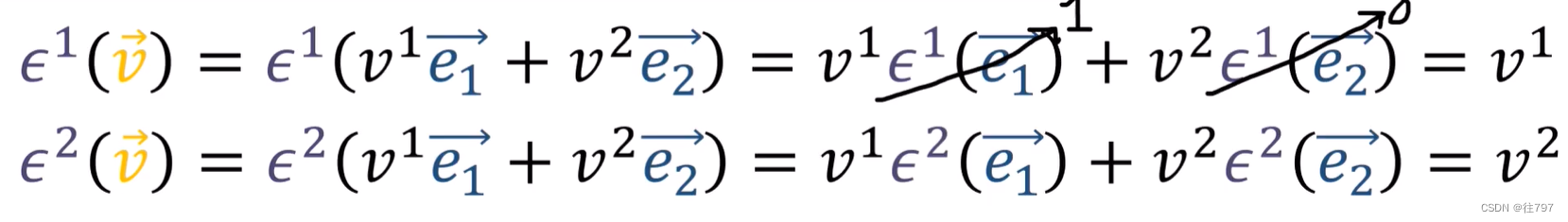
仔细 看,这些 所做的是:它们在投射矢量分量,是把?
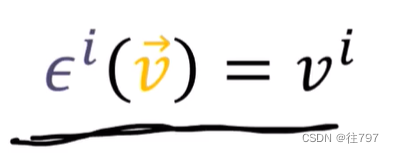
当把应用到v中,我们将得到v基向量e1、e2上的组件,
所以,看起来就像是:可以帮助我们获得向量v的第一个分量,其中e1就是指向这个分量的方向。
看起来就像是:可以帮助我们获得向量v的第2个分量,其中e2就是指向这个分量的方向。
这就是协向量的样子(视觉上)

现在我们对向量v应用一些通用的协向量α,α可以是任一协向量
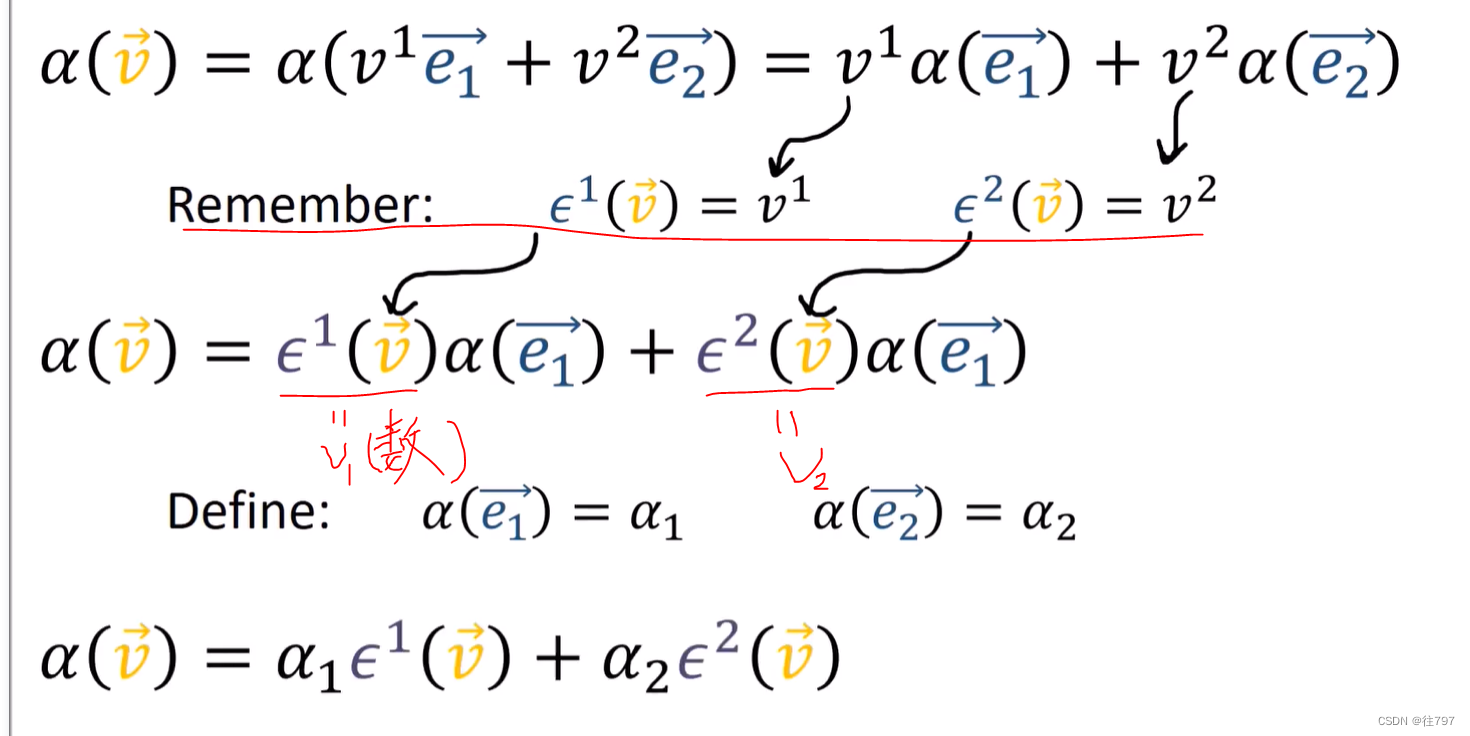
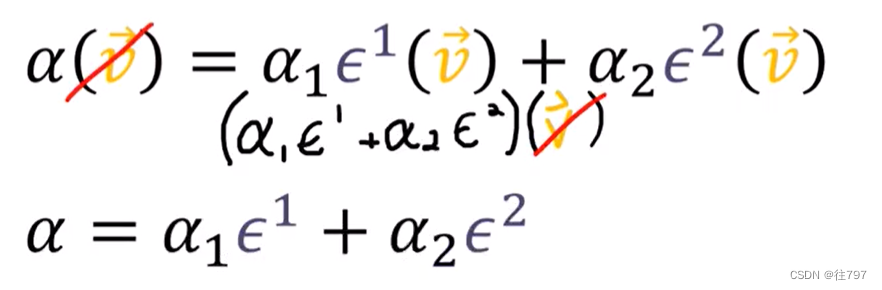
(注:α1=α*e1=一个数,α2也是一个数,上面表示 任意一个协向量α = 数1* + 数2*
)
所以上面我们所作的是:编写了一个通用的协向量α(α可以是任意协向量) 作为协向量的线性组合,
所以这意味着协向量 是 构成了所有协向量集合的基底,
也因为这个原因,被称为 ”对偶基“ , 因为它们是对偶空间V* 上的 基底。
以上我们就用了代数的方式写出了 一个协向量的表达,
现考虑视觉上,
假设有一个协向量α,一簇在e1、e2为基底的向量空间的线, 可通过把α应用到基底e1、e2上来获得α的组件,只需计算穿透的行数,
我们可以把α写成、
的线性组合 的方式来表示α。
所以过程就是:从基底向量开始,使用这个定义 来获得对偶协向量的基底,然后使用 这些 我们就可以将任意的协向量表示为对偶基的线性组合。(这是对上面整个过程的描述)
但记住,、
并不是 唯一的基底,(正如向量空间那般,基底可以变,基底个数不变那般)
因此,我们可以用别的向量开始,如:
并使用以下规则,我们可以定义另一对对偶基,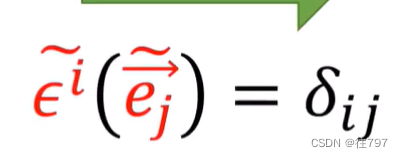 (规则--就是规定)
(规则--就是规定)
同样地,可将任意协向量α表示为 、
的线性组合。

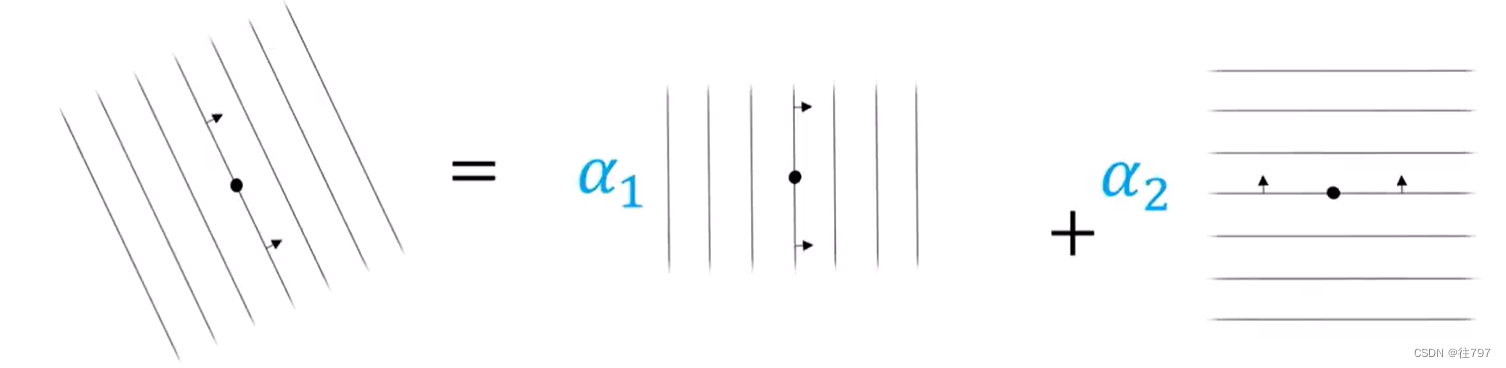
例子:
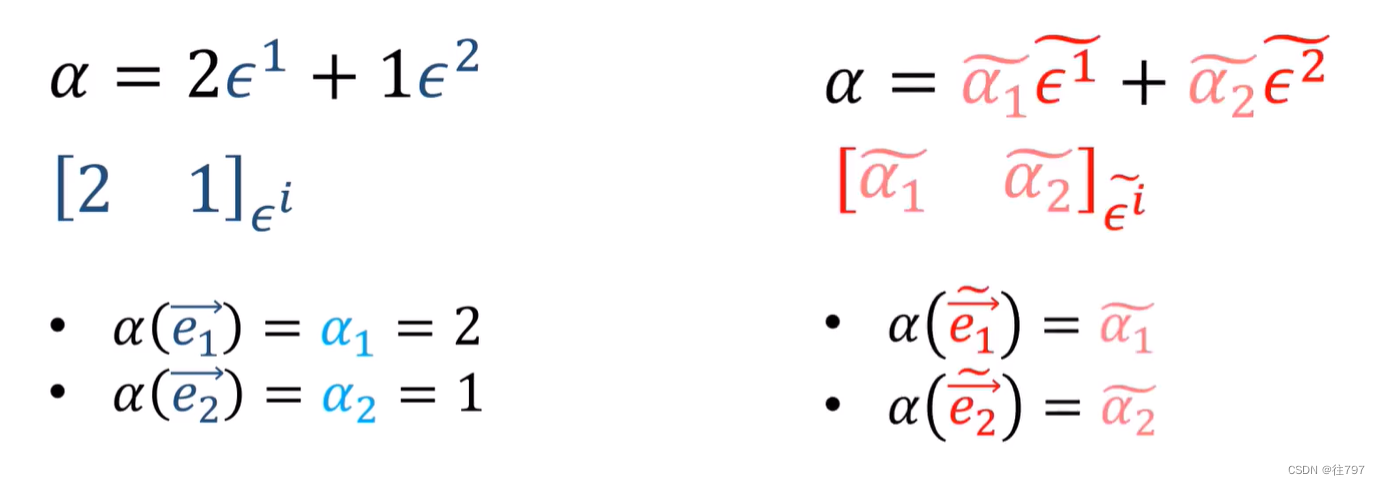
已知一个协向量α在 旧(对偶)基、
下的线性表示, 同时有一对新(对偶)基
、
,想把协向量α利用新基
、
做线性表示,
将α应用到新基底,
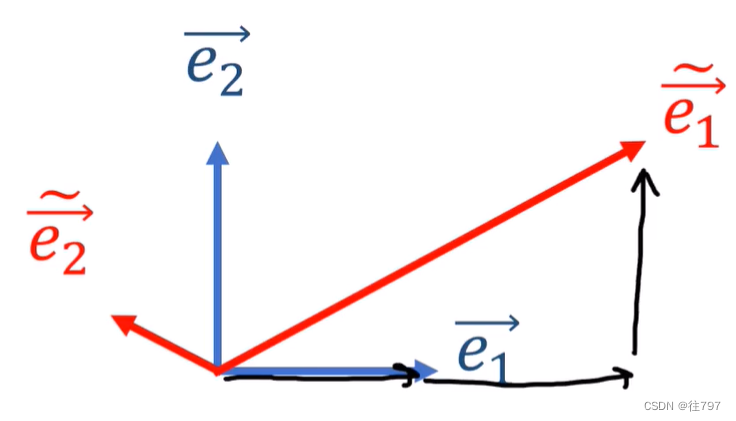
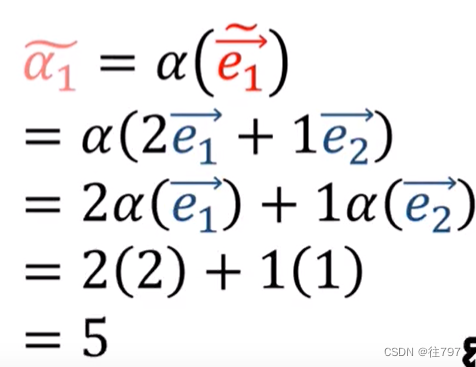
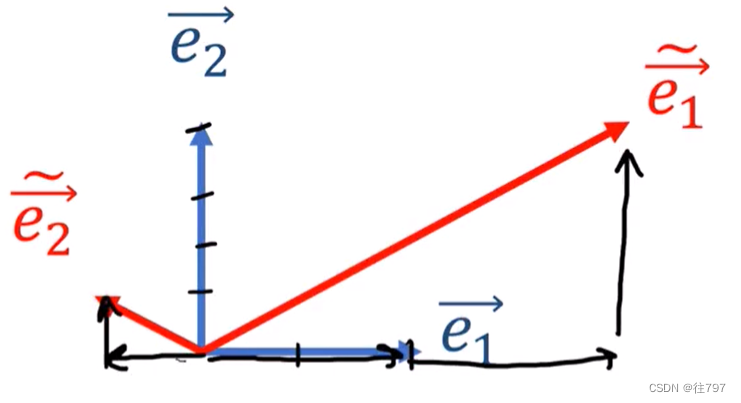
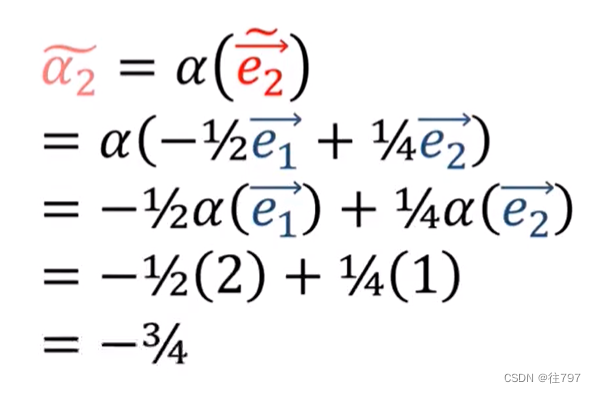
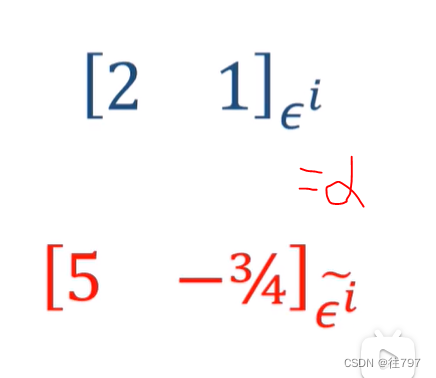
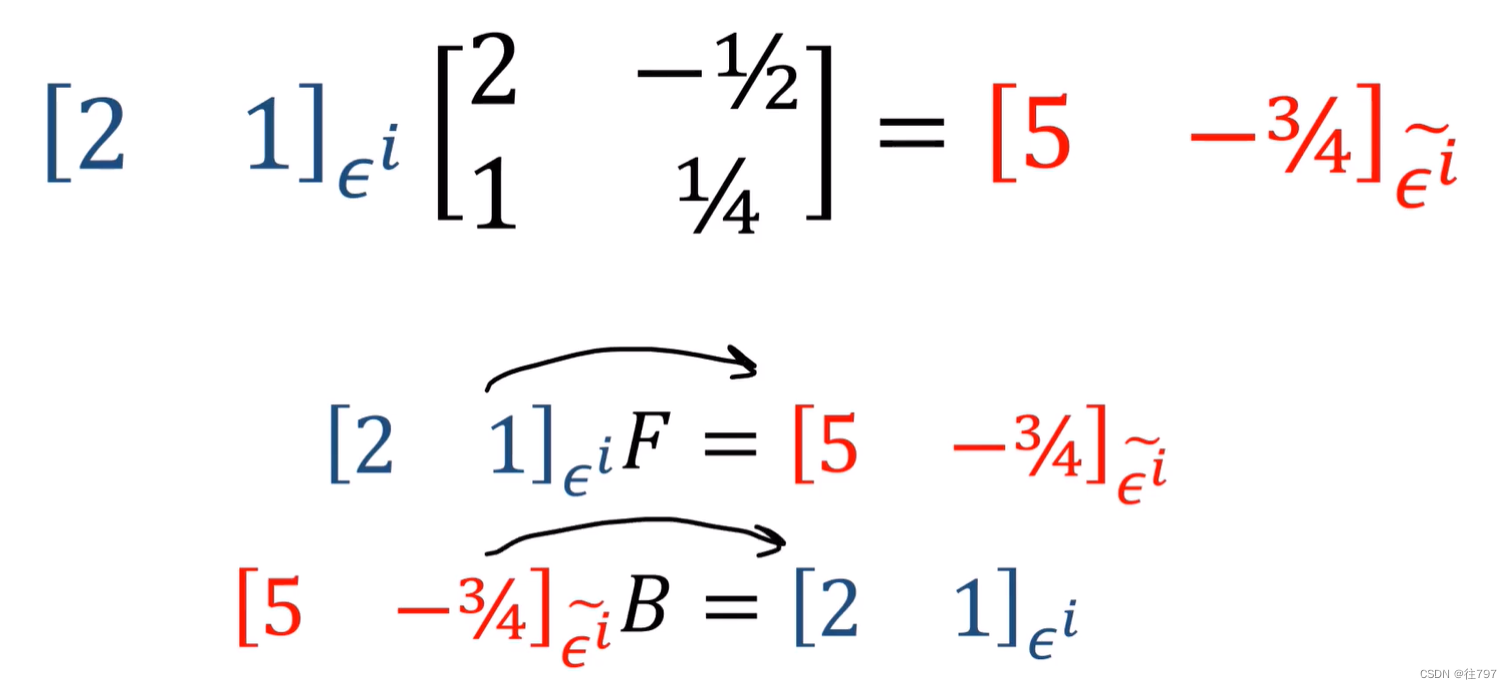
以上是向量的转换;
以下是基底的转换;
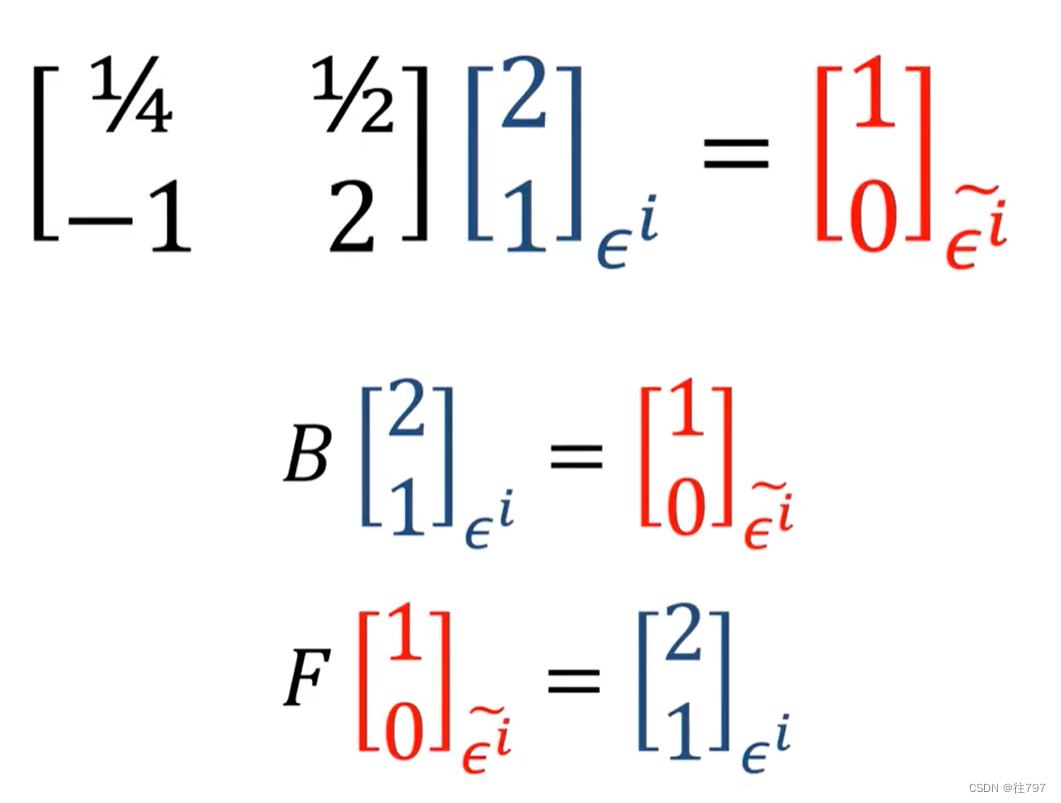
仔细观察,协向量中:基底的转换: 旧基到新基---用B,新基到旧基===用F;
这与向量的完全相反!
协向量中:某个协向量的转换:利用旧基到利用新基---用F,利用新基到利用旧基--用B
这与向量的完全相反!
这就是为什么不能只翻转列向量来获得行向量,--------这在正交基上有效,
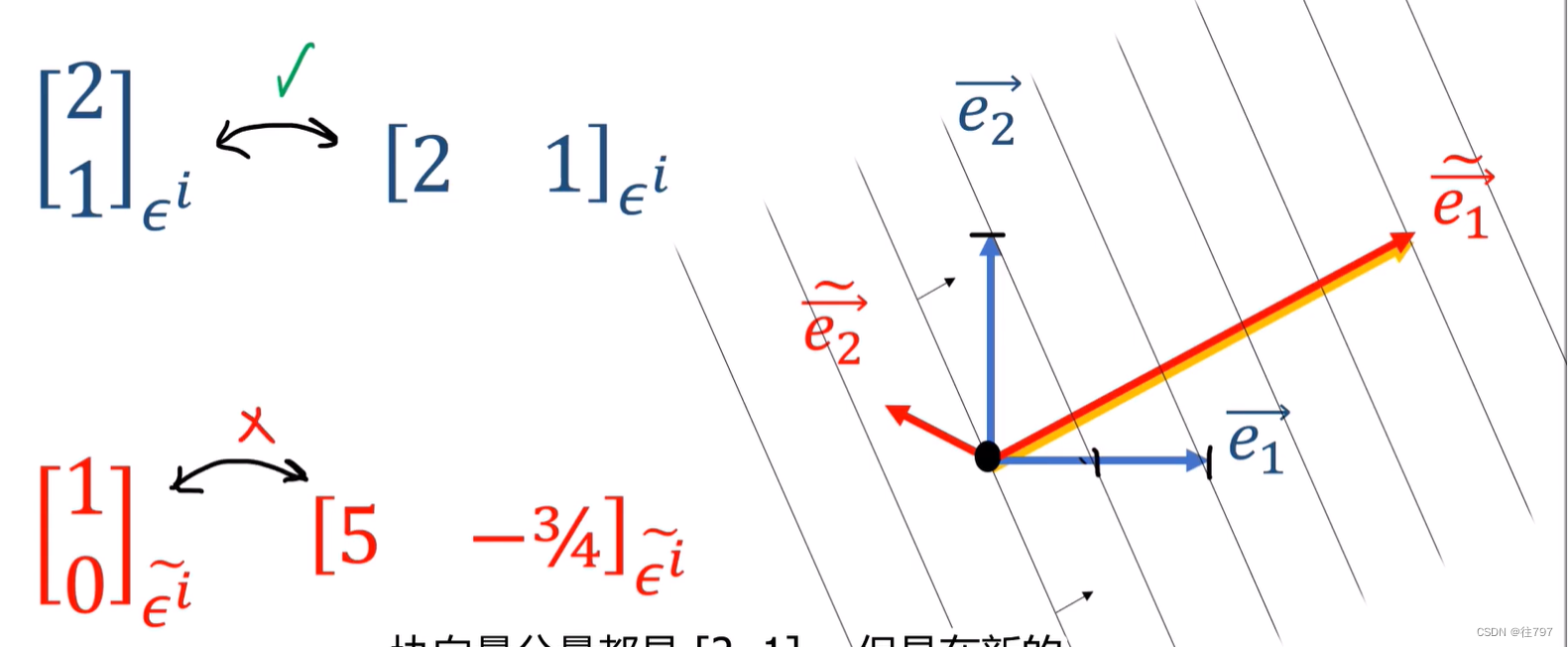
你看上图, 对于利用正交基, 协向量你把它从列向量转置成行向量,2,1仍是2,1;
但是,一旦不是正交基了, 【1;0】变为 【5,-3/4】明显不能靠转置来获得。
所以,向量分量是通过计算构建向量时使用了多少基向量来测量的,
但是协向量分量是通过计算 基向量 穿过的协向量线的数量来测量的。
相关文章:

7.Tensors For Beginneers - Convector Components
介绍协向量时,曾说过它们有点像 行向量, 行向量确实以某种方式代表了协向量, 这里说明一下: 协向量是不变的; 协向量组件是可变的。 协向量不依赖坐标系,协向量的组件取决于坐标系。 当我们说协向量具有组…...

直线导轨坏了可以维修吗?
直线导轨是工业自动化设备中常用的零部件,其性能和使用寿命对设备的稳定运行和产能有着直接的影响,在生产中,由于各种原因,直线导轨会出现各种问题,那么,直线导轨的维修方法究竟是怎样的呢?我们…...

Java基础--泛型详解
一、背景 java推出泛型之前,集合元素类型可以是object类型,能够存储任意的数据类型对象,但是在使用过程中,如果不知道集合里面的各个元素的类型,在进行类型转换的时候就很容易引发ClassCastException异常。 二、概念 …...
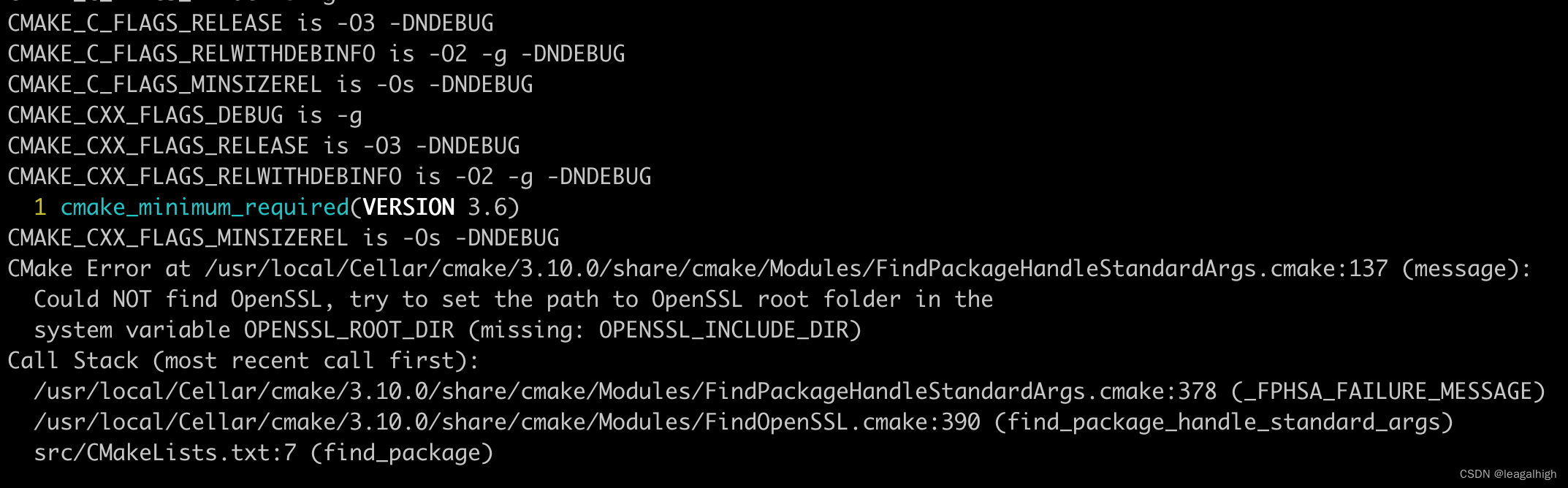
学习搜狗的workflow,MacBook上如何编译
官网说可以在MacBook上也可以运行,但是编译的时候却有找不到openssl的错误: 看其他博客也有类似的错误,按照类似的思路去解决 问题原因和解决办法 cmake编译的时候,没有找到openssl的头文件,需要设置cmake编译环境下…...
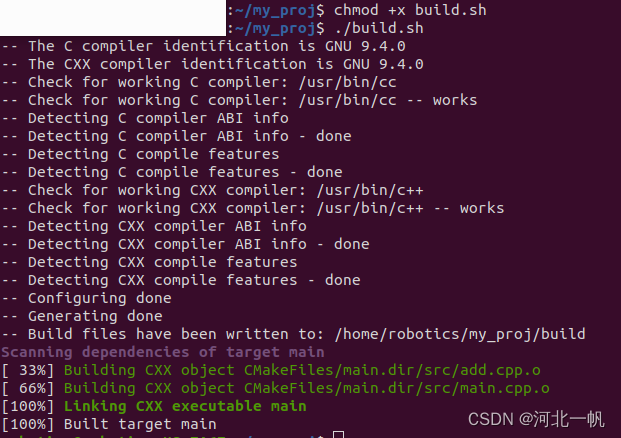
Ubuntu使用cmake和vscode开发自己的项目,引用自己的头文件和openCV
创建文件夹 mkdir my_proj 继续创建include 和 src文件夹,形成如下的目录结构 用vscode打开项目 创建add.h #ifndef ADD_H #define ADD_Hint add(int numA, int numB);#endif add.cpp #include "add.h"int add(int numA, int numB) {return numA nu…...
 dataset, dataloader)
2) dataset, dataloader
dataset, dataloader torchvision.datasets里面集成了一些常见的数据集,例如MNIST和CIFAR10 1) Dataset 以MNIST为例,其使用方式如下 import torch import torchvision from torchvision import transformstrain_dataset = torchvision.datasets.MNIST(root=../data,trai…...

阿里云PolarDB自研数据库详细介绍_兼容MySQL、PostgreSQL和Oracle语法
阿里云PolarDB数据库是阿里巴巴自研的关系型分布式云原生数据库,PolarDB兼容三种数据库引擎:MySQL、PostgreSQL、Oracle(语法兼容),目前提供云原生数据库PolarDB MySQL版、云原生数据库PolarDB PostgreSQL版和云原生数…...
[软件工具]opencv-svm快速训练助手教程解决opencv C++ SVM模型训练与分类实现任务支持C# python调用
opencv中已经提供了svm算法可以对图像实现多分类,使用svm算法对图像分类的任务多用于场景简单且对时间有要求的场景,因为opencv的svm训练一般只需要很短时间就可以完成训练任务。但是目前网上没有一个工具很好解决训练问题,大部分需要自己编程…...
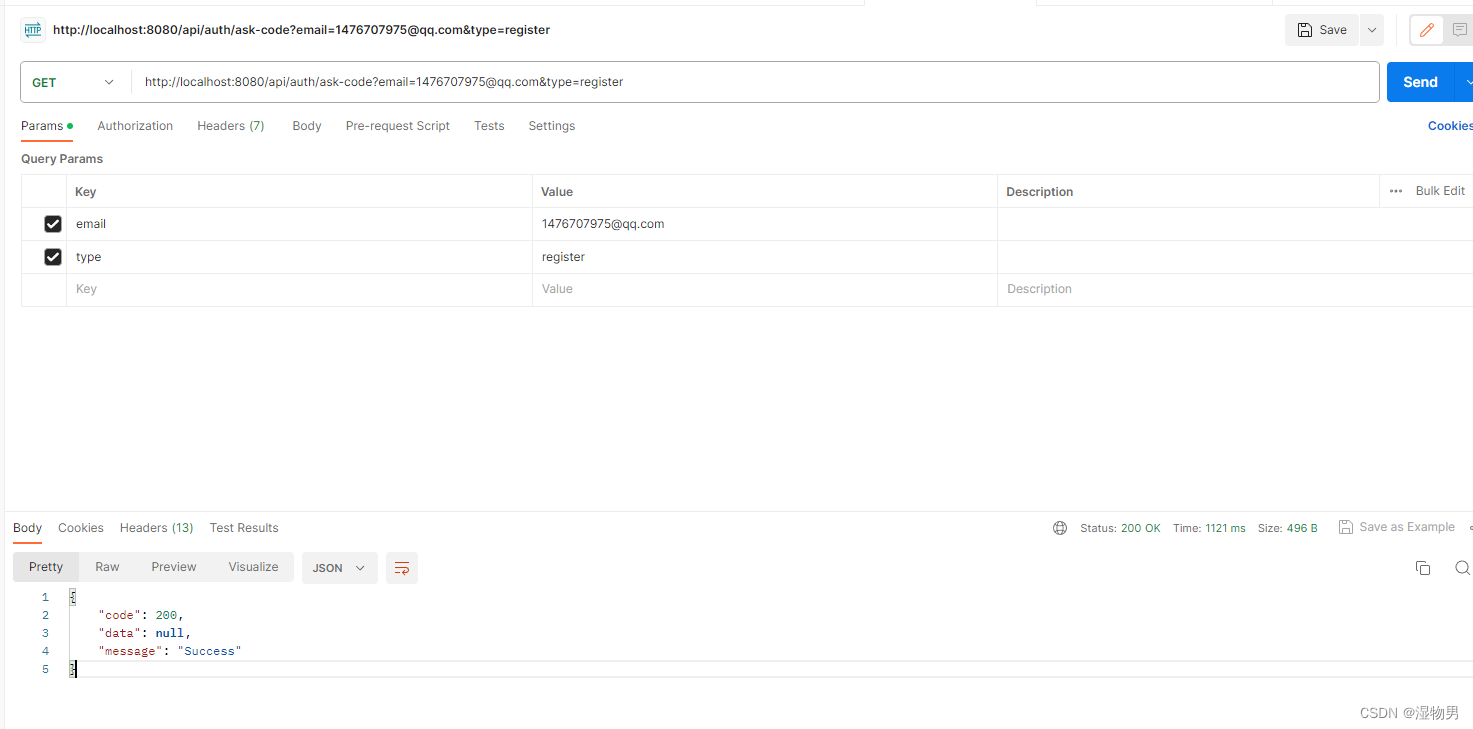
邮件注册(一)验证码发送
通过邮箱实现注册,用户请求验证码完成注册操作。 导入依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId></dependency><dependency><g…...
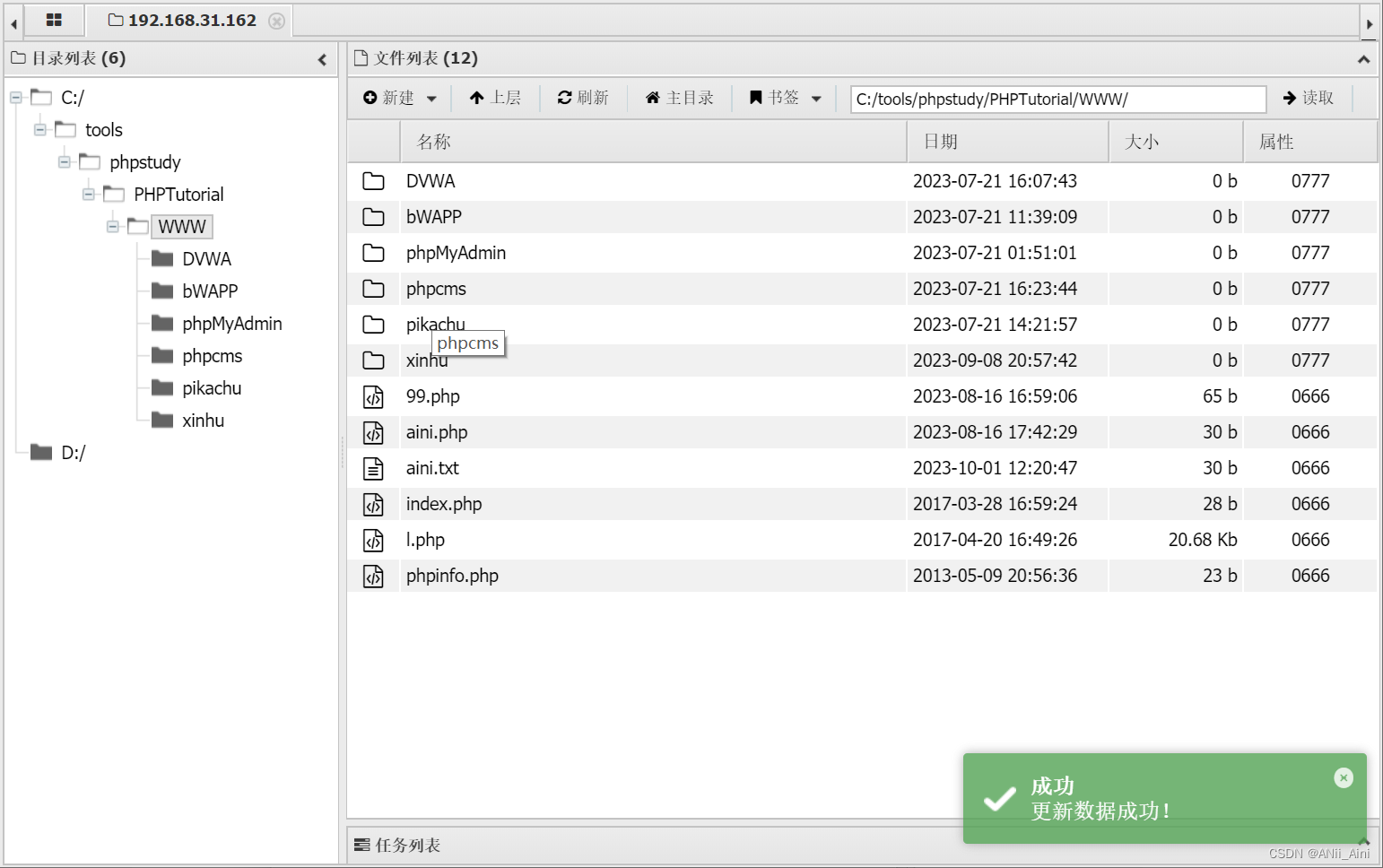
【网络安全---sql注入(2)】如何通过SQL注入getshell?如何通过SQL注入读取文件或者数据库数据?一篇文章告诉你过程和原理。
前言 本篇博客主要是通过piakchu靶场来讲解如何通过SQL注入漏洞来写入文件,读取文件。通过SQL输入来注入木马来getshell等,讲解了比较详细的过程; 如果想要学习SQL注入原理以及如何进行SQL注入,我也写了一篇详细的SQL注入方法及…...
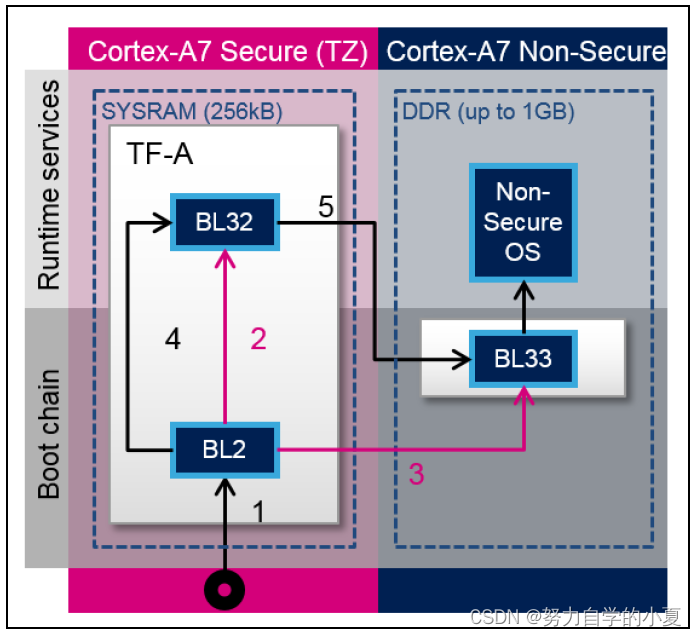
正点原子嵌入式linux驱动开发——TF-A移植
经过了之前的学习,除了TF-A的详细启动流程仍待更新,TF-A的使用和其对应的大致启动流程已经进行过了学习。但是当我们实际做产品时,硬件平台肯定会和ST官方的有区别,比如DDR容量会改变,自己的硬件没有使用到官方EVK开发…...
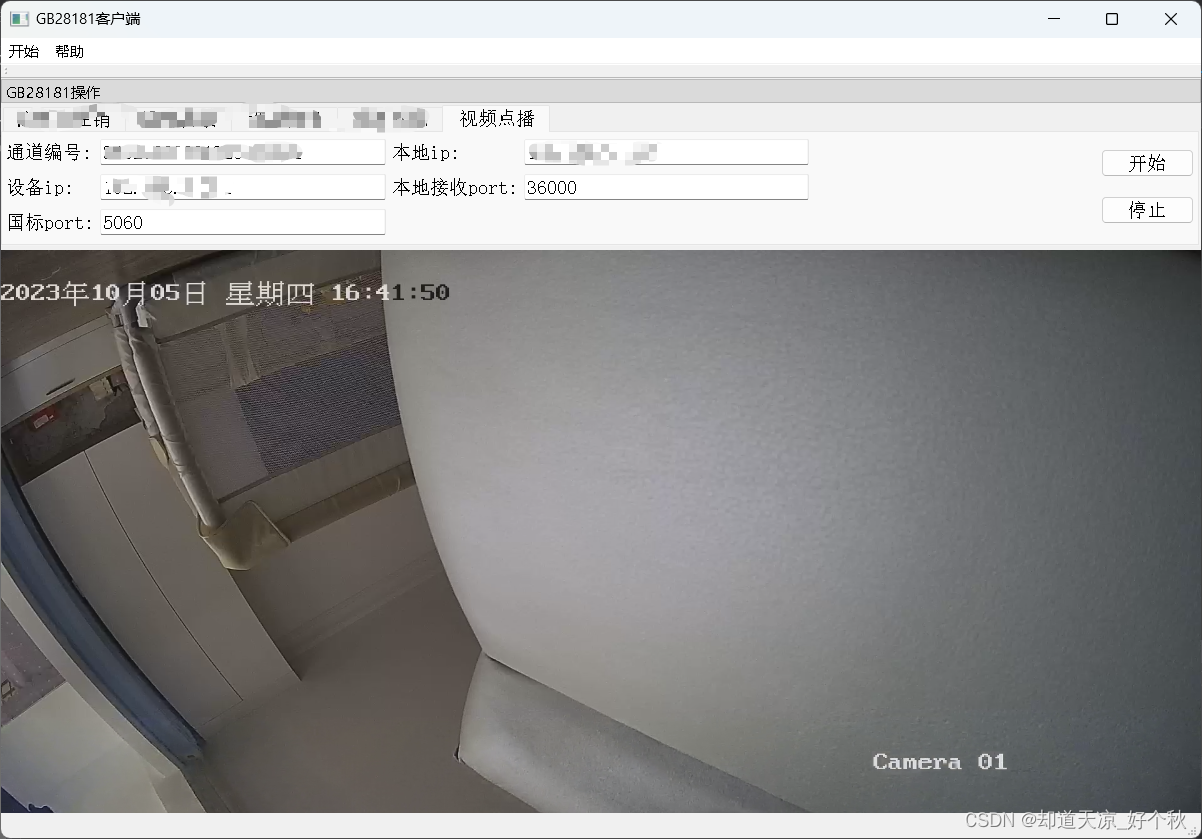
GB28181学习(六)——实时视音频点播(数据传输部分)
GB28181系列文章: 总述:https://blog.csdn.net/www_dong/article/details/132515446 注册与注销:https://blog.csdn.net/www_dong/article/details/132654525 心跳保活:https://blog.csdn.net/www_dong/article/details/132796…...
JMeter接口自动化测试(数据驱动)
之前我们的用例数据都是配置在HTTP请求中,每次需要增加,修改用例都需要打开JMeter重新编辑,当用例越来越多的时候,用例维护起来就越来越麻烦,有没有好的方法来解决这种情况呢?我们可以将用例的数据存放在cs…...

数据结构:二叉树(超详解析)
目录 1.树概念及结构 1.1树的概念 1.2树的相关概念 1.3树的表示 1.3.1孩子兄弟表示法: 1.3.2双亲表示法:只存储双亲的下标或指针 两节点不在同一树上: 2.二叉树概念及结构 2.1.概念 2.2.特殊的二叉树: 2…...

【考研数学】高等数学第七模块 —— 曲线积分与曲面积分 | 4. 对坐标的曲面积分(第二类曲面积分)与场论初步
文章目录 二、曲面积分2.2 对坐标的曲面积分(第二类曲面积分)1. 问题产生 —— 流量2. 对坐标的曲面积分的定义(了解)3. 对坐标的曲面积分的性质4. 对坐标的曲面积分的计算法(1) 二重积分法(2&a…...
使用Thrift实现跨语言RPC调用
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
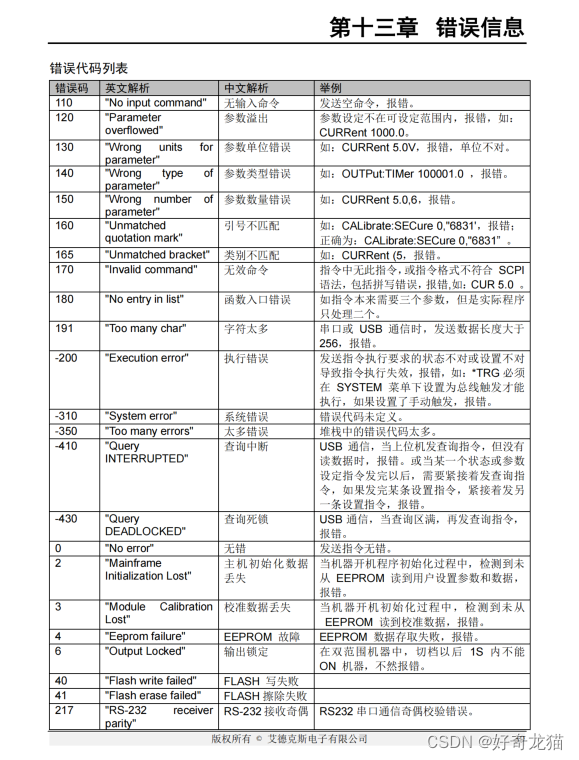
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】
【QT5-程序控制电源-RS232-SCPI协议-上位机-基础样例【1】】 1、前言2、实验环境3、自我总结1、基础了解仪器控制-熟悉仪器2、连接SCPI协议3、选择控制方式-程控方式-RS2324、代码编写 4、熟悉协议-SCPI协议5、测试实验-测试指令(1)硬件连接(…...

leetcode 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零
1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果…...

Error string: Could not load library
启动Rivz时,报错: Error string: Could not load library (Poco exception libg2o_csparse_extension.so.0.1: cannot open shared object file: No such file or directory) [ERROR] [1696572310.529059051]: Failed to load nodelet [/radar_graph_s…...

pom.xml里的标签
pom.xml 是 Maven 项目的配置文件,其中包含了各种配置信息和依赖管理。下面是一些常见的 pom.xml 中的标签和其作用的简要说明: <project>:根标签,定义了整个项目的基本信息和结构。 <groupId>:指定项目所…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...
