CentOS 7 上编译和安装 SQLite 3.9.0
文章目录
- 可能报错分析
- 详细安装过程
可能报错分析
报错如下:
django.core.exceptions.ImproperlyConfigured: SQLite 3.9.0 or later is required (found 3.7.17).
原因:版本为3.7.太低了,需要升级到3.9.0至少
详细安装过程
1.安装所需的编译工具:
sudo yum install gcc make autoconf automake libtool
2.下载 SQLite 3.9.0 的源代码:
wget https://sqlite.org/2015/sqlite-autoconf-3090000.tar.gz
3.解压缩源代码:
tar xvf sqlite-autoconf-3090000.tar.gz
4.进入解压后的目录:
cd sqlite-autoconf-3090000
5.配置 SQLite 的编译选项:
./configure --prefix=/usr/local
6.编译 SQLite:
make
7.安装 SQLite:
sudo make install
8.验证版本:
sqlite3 --version
成功:

相关文章:

CentOS 7 上编译和安装 SQLite 3.9.0
文章目录 可能报错分析详细安装过程 可能报错分析 报错如下: django.core.exceptions.ImproperlyConfigured: SQLite 3.9.0 or later is required (found 3.7.17). 原因:版本为3.7.太低了,需要升级到3.9.0至少 详细安装过程 1.安装所需的…...

[GXYCTF2019]禁止套娃 无回显 RCE 过滤__FILE__ dirname等
扫除git 通过githack 获取index.php <?php include "flag.php"; echo "flag在哪里呢?<br>"; if(isset($_GET[exp])){if (!preg_match(/data:\/\/|filter:\/\/|php:\/\/|phar:\/\//i, $_GET[exp])) {if(; preg_replace(/[a-z,_]\(…...

Springboot使用Aop保存接口请求日志到mysql
1、添加aop依赖 <!-- aop日志 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId></dependency> 2、新建接口保存数据库的实体类RequestLog.java package com.example…...
网络安全面试题汇总(附答案)
作为从业多年的网络安全工程师,我深知在面试过程中面试官所关注的重点及考察的技能点。网络安全作为当前信息技术领域中非常重要的一部分,对于每一个从事网络安全工作的人员来说,不仅需要掌握一定的技术能力,更需要具备全面的综合…...

Centos7安装kvm,配置虚拟机网络
1.安装软件包,禁用防火墙(非必须) yum -y install qemu-kvm libvirt virt-install 1)禁用防火墙(非必须) systemctl stop firewalld systemctl disable firewalld 2)禁用NetworkManager syst…...

Javascript文件上传
什么是文件上传 文件上传包含两部分, 一部分是选择文件,包含所有相关的界面交互。一部分是网络传输,通过一个网络请求,将文件的数据携带过去,传递到服务器中,剩下的,在服务器中如何存储…...
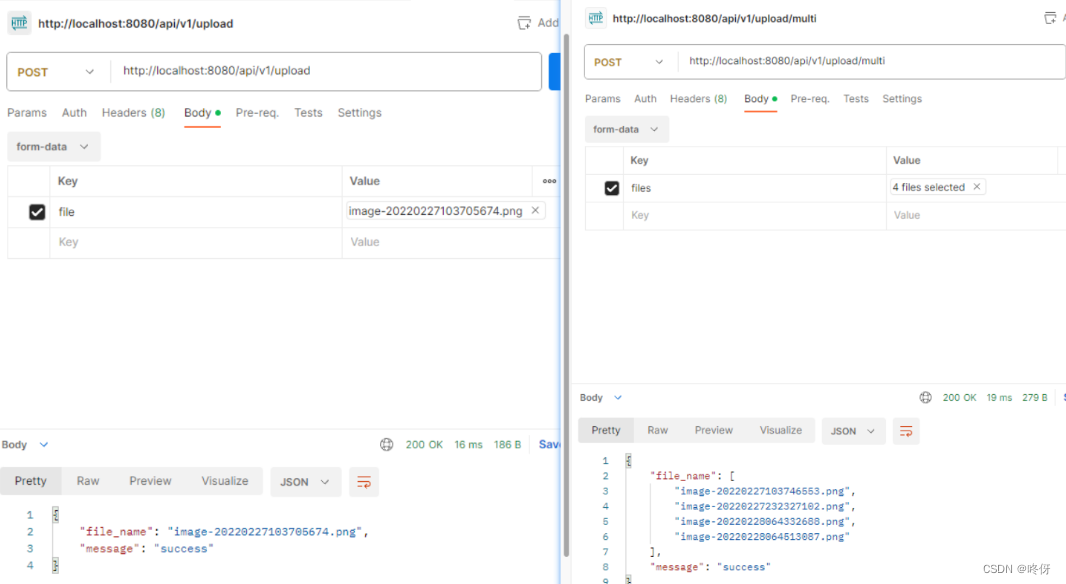
golang gin——文件上传(单文件,多文件)
文件上传 单文件上传 从form-data获取文件 package uploadimport ("github.com/gin-gonic/gin""net/http" ) // 单文件上传,多文件上传 func Upload(c *gin.Context) {file, _ : c.FormFile("file") // file为字段名dst : "…...

面试题:Redis和MySQL的事务区别是什么?
大家好,我是小米!今天我要和大家聊聊一个在技术面试中经常被问到的问题:“Redis和MySQL的事务区别是什么?”这个问题看似简单,但实际上涉及到了数据库和缓存两个不同领域的知识,让我们一起来深入了解一下吧…...

Canvas绘图
Canvas绘图 Canvas的意义 随着前端的不断发展,页面特效越来越炫酷,W3C组织也不断退出新的CSS特性:例如各种渐变,瀑布流布局,各种阴影,但是随着需求越来越花哨,W3C表示:我去你妈的&…...
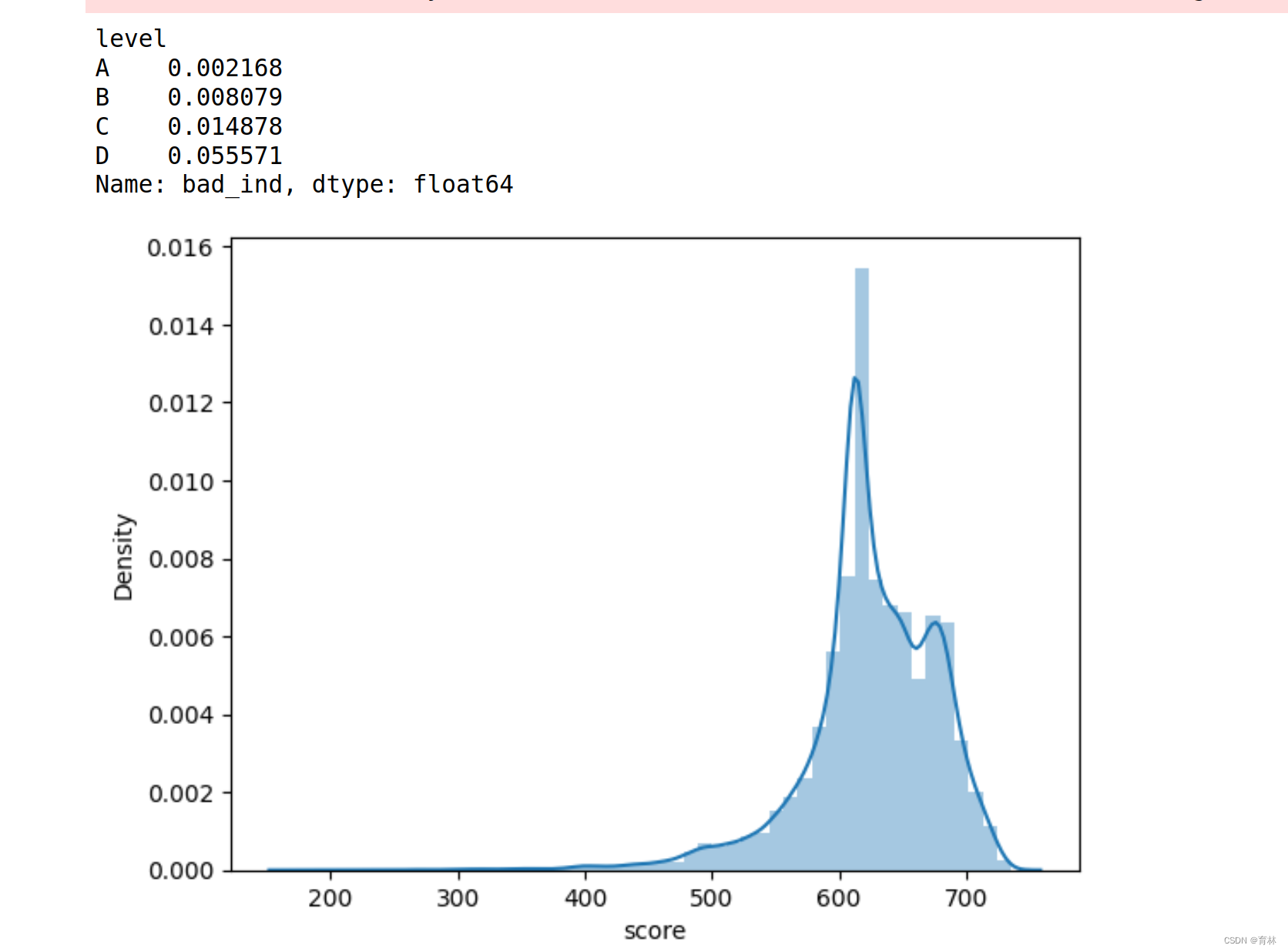
逻辑回归评分卡
文章目录 一、基础知识点(1)逻辑回归表达式(2)sigmoid函数的导数损失函数(Cross-entropy, 交叉熵损失函数)交叉熵求导准确率计算评估指标 二、导入库和数据集导入库读取数据 三、分析与训练四、模型评价ROC曲线KS值再做特征筛选生成报告 五、行为评分卡模型表现总结 一、基础知…...

DPDK系列之三十三DPDK并行机制的底层支持
一、背景介绍 在前面介绍了DPDK中的上层对并行的支持,特别是对多核的支持。但是,大家都知道,再怎么好的设计和架构,再优秀的编码,最终都要落到硬件和固件对整个上层应用的支持。单纯的硬件好处理,一个核不…...
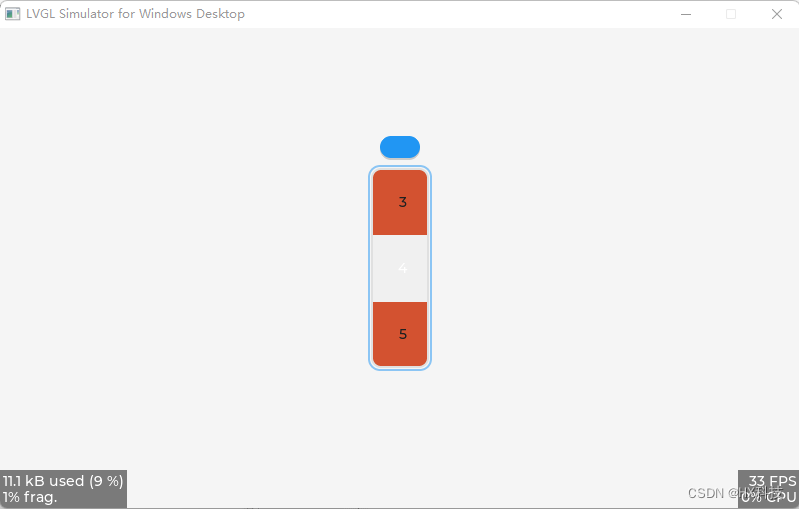
LVGL_基础控件滚轮roller
LVGL_基础控件滚轮roller 1、创建滚轮roller控件 /* 创建一个 lv_roller 部件(对象) */ lv_obj_t * roller lv_roller_create(lv_scr_act()); // 创建一个 lv_roller 部件(对象),他的父对象是活动屏幕对象// 将部件(对象)添加到组,如果设置了默认组,…...
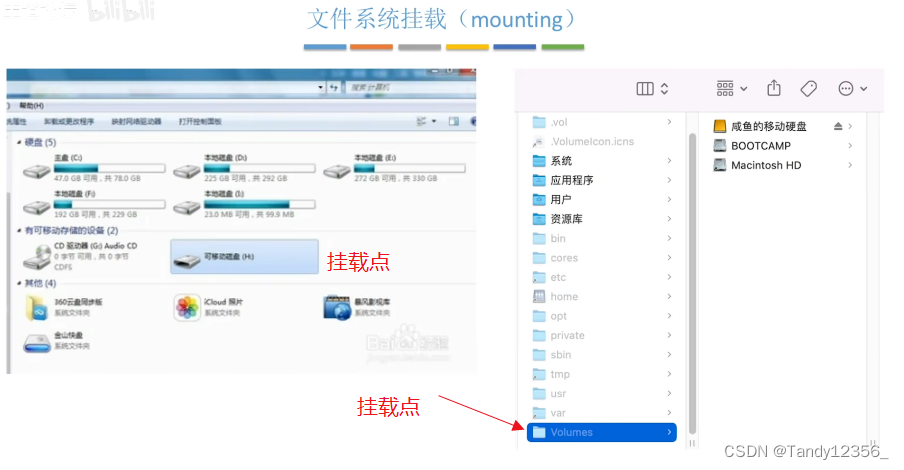
王道考研操作系统——文件管理
磁盘的基础知识 .txt用记事本这个应用程序打开,文件最重要的属性就是文件名了 保护信息:操作系统对系统当中的各个用户进行了分组,不同分组的用户对文件的操作权限是不一样的 文件的逻辑结构就是文件内部的数据/记录应该被怎么组织起来&…...
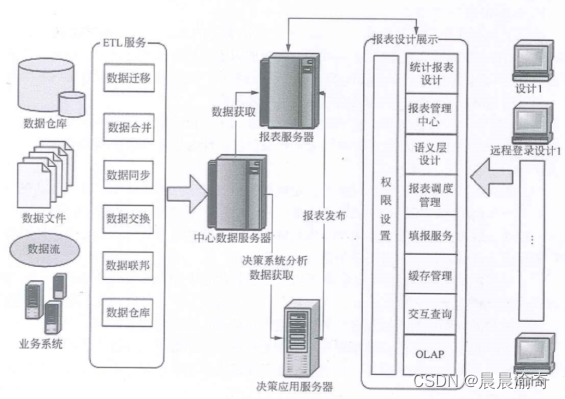
商业智能系统的主要功能包括数据仓库、数据ETL、数据统计输出、分析功能
ETL服务内容包含: 数据迁移数据合并数据同步数据交换数据联邦数据仓库...

基于帝国主义竞争优化的BP神经网络(分类应用) - 附代码
基于帝国主义竞争优化的BP神经网络(分类应用) - 附代码 文章目录 基于帝国主义竞争优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.帝国主义竞争优化BP神经网络3.1 BP神经网络参数设置3.2 帝国主义竞争算…...

将python项目部署在一台服务器上
将python项目部署在一台服务器上 1.服务器2.部署方法2.1 手动部署2.2 容器化技术部署2.3 服务器less技术部署 1.服务器 服务器一般为:物理服务器和云服务器。 我的是物理服务器:这是将服务器硬件直接放置在您自己的数据中心或机房的传统方法。这种方法需…...
【C语言】善于利用指针(二)
💗个人主页💗 ⭐个人专栏——C语言初步学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 导读:1. 字符指针1.1 字符串的引用方式1.2 有趣的面试题 2. 数组指针2.1 一维数组指针的定义2.2 一维数组…...

Python调用C++
https://www.cnblogs.com/renfanzi/p/10276997.html Linux使用Python调用C/C接口(一) - 代码先锋网 linux系统上使用Python调用C生成的.so动态链接库opencv_linux 下python 编译为so ,给c使用_比赛学习者的博客-CSDN博客 https://www.cnblogs.com/shuimuqingyang/p/13618105…...
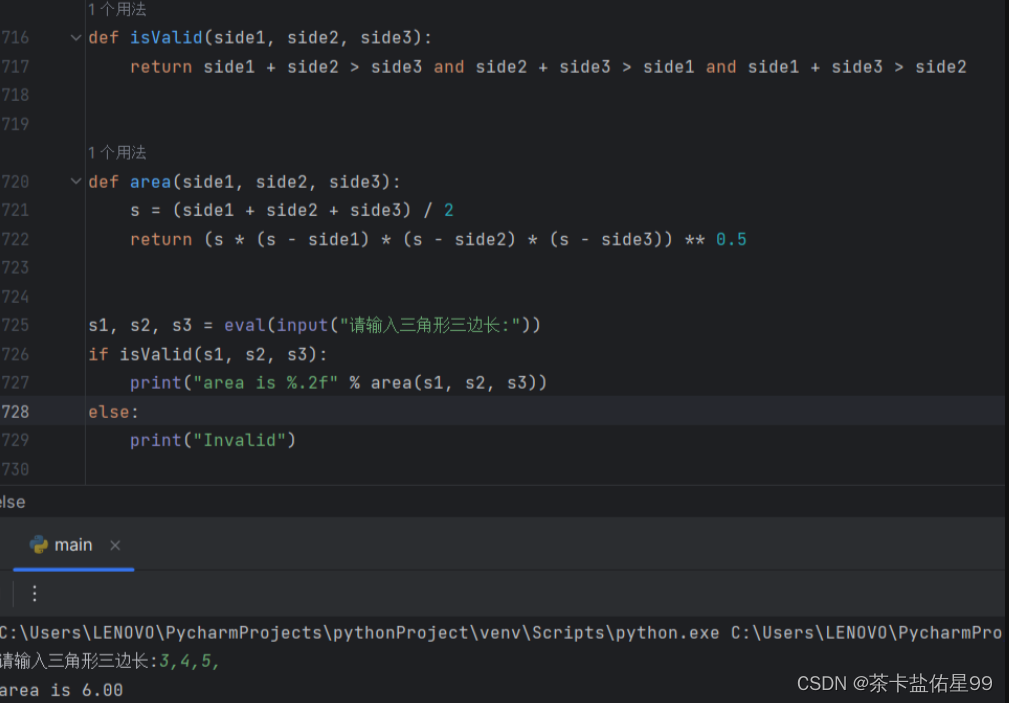
自己实现扫描全盘文件的函数。
1.自己实现扫描全盘的函数 def scan_disk(dir): global count,dir_count if os.path.isdir(dir): files os.listdir(dir) for file in files: print(file) dir_count 1 if os.path.isdir(dir os.sep file): …...

JSON文件读写
1、依赖文件 #include <QFile> #include <QJsonDocument> #include <QJsonObject> #include <QDebug> #include <QStringList>2、头文件 bool ReadJsonFile(const QString& filePath""); bool WriteJsonFile(const QString&…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
