C++树详解
树
树的定义
树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:①有且仅有一个特定的称为根(Root)的结点;②当n>1时,其余结点可分为m(m>0)个互不相交的有限集T 1 {T}_{1}T 1 、T 2 {T}_{2}T 2 、… 、T m {T}_{m}T m ,其中每一个集合本身又是一棵树,并且称为根的子树(Sub Tree)。树的基本术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
二叉树
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构。
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
⼆叉树的种类
⼆叉树有两种主要的形式:满⼆叉树和完全⼆叉树。
满二叉树
在一棵二叉树中,如果所有的分支节点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树成为满二叉树。
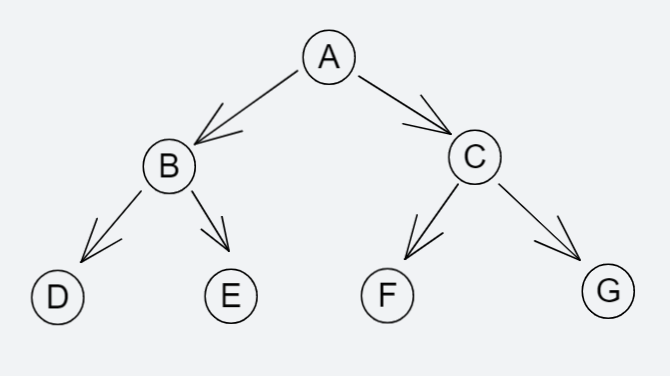
完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为 i(1 ≤ i ≤ n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同,则这棵二叉树称为完全二叉树
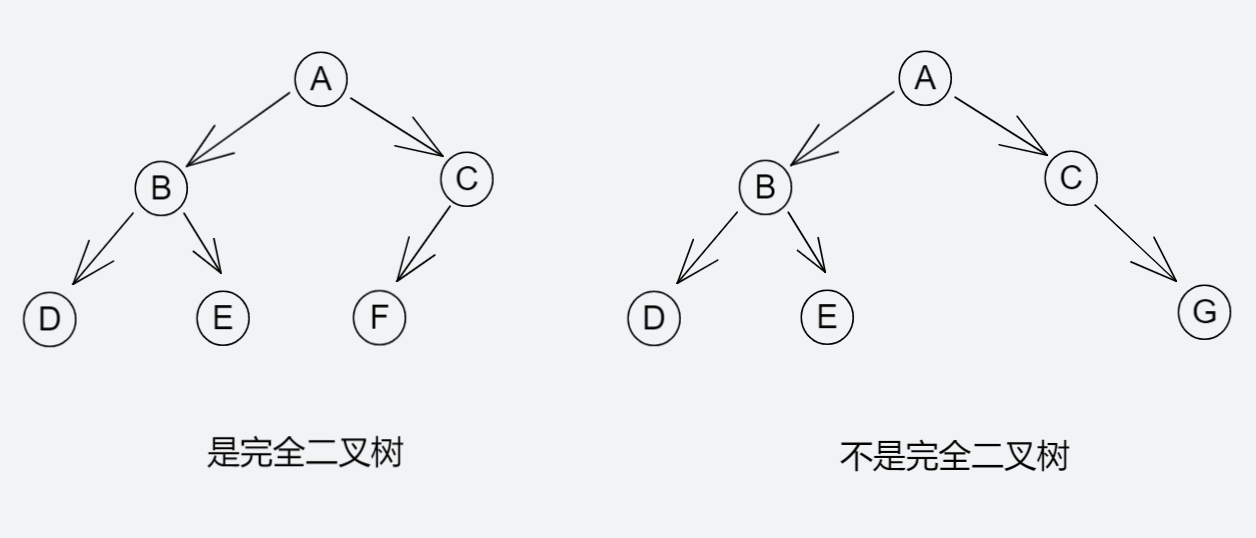
二叉树的性质
二叉树的第 i 层至多有2 i − 1 {2}^{i-1}2 i−1 个结点; 深度为 k 的二叉树至多有2 k {2}^{k}2 k -1个结点; 对任何一棵二叉树T,如果其终端结点的个数(也就是叶子节点数)为n 0 {n}_{0}n 0 ,度为2的结点个数为n 2 {n}_{2}n 2 ,则n 0 {n}_{0}n 0 =n 2 {n}_{2}n 2 +1。(大话数据结构P143)二叉树的遍历方法
二叉树的遍历方式主要可以分为四种:前序遍历、中序遍历、后序遍历和层序遍历。
前序遍历
简单记为中左右,也就是说先访问根节点,然后前序遍历左子树,再前序遍历右子树。
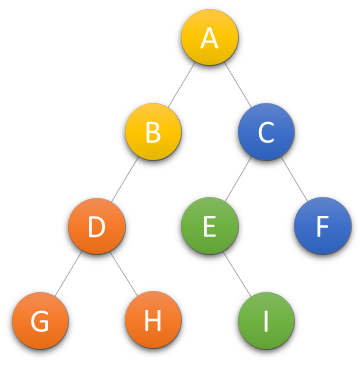
遍历的顺序为ABDGHCEIF
中序遍历
简单记为左中右,也就是说先访问二叉树最左边的结点,然后再访问中间的结点,最后再访问右边的结点。·

遍历的顺序为GDHBAEICF
后序遍历
简单记为左右中,也就是说先访问二叉树最左边的结点,然后再访问右边的结点,最后再访问中间的结点。·

遍历的顺序为GHDBIEFCA
层序遍历
从根结点开始访问,从上而下逐层遍历,在同一层中·,按从左到右的顺序对结点逐个访问。

遍历的顺序为ABCDEFGHI
前序遍历、中序遍历和后序遍历就是中的位置不一样,前序遍历就是中左右,中序遍历就是左中右,后序遍历就是左右中。
前中后序遍历都是深度搜索,层序遍历是广度搜索。
二叉树的实现
⼆叉树的定义
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
使用前序遍历创建二叉树
void CreatTreeNode(TreeNode*&T){char c;cin >> c;if(c=='*'){T = NULL;return;}else{ T = new TreeNode;T->val = c;CreatTreeNode(T->left);CreatTreeNode(T->right);}
}
前序遍历
class Solution {
public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val); // 中traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
中序遍历
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左vec.push_back(cur->val); // 中traversal(cur->right, vec); // 右
}
后序遍历
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右vec.push_back(cur->val); // 中
}
相关文章:

C++树详解
树 树的定义 树(Tree)是n(n≥0)个结点的有限集。n0时称为空树。在任意一颗非空树中:①有且仅有一个特定的称为根(Root)的结点;②当n>1时,其余结点可分为m(…...

支付环境安全漏洞介绍
1、平台支付逻辑全流程分析 2、平台支付漏洞如何利用?买东西还送钱? 3、BURP抓包分析修改支付金额,伪造交易状态? 4、修改购物车参数实现底价购买商品 5、SRC、CTF、HW项目月入10W副业之路 6、如何构建最适合自己的网安学习路线 1…...
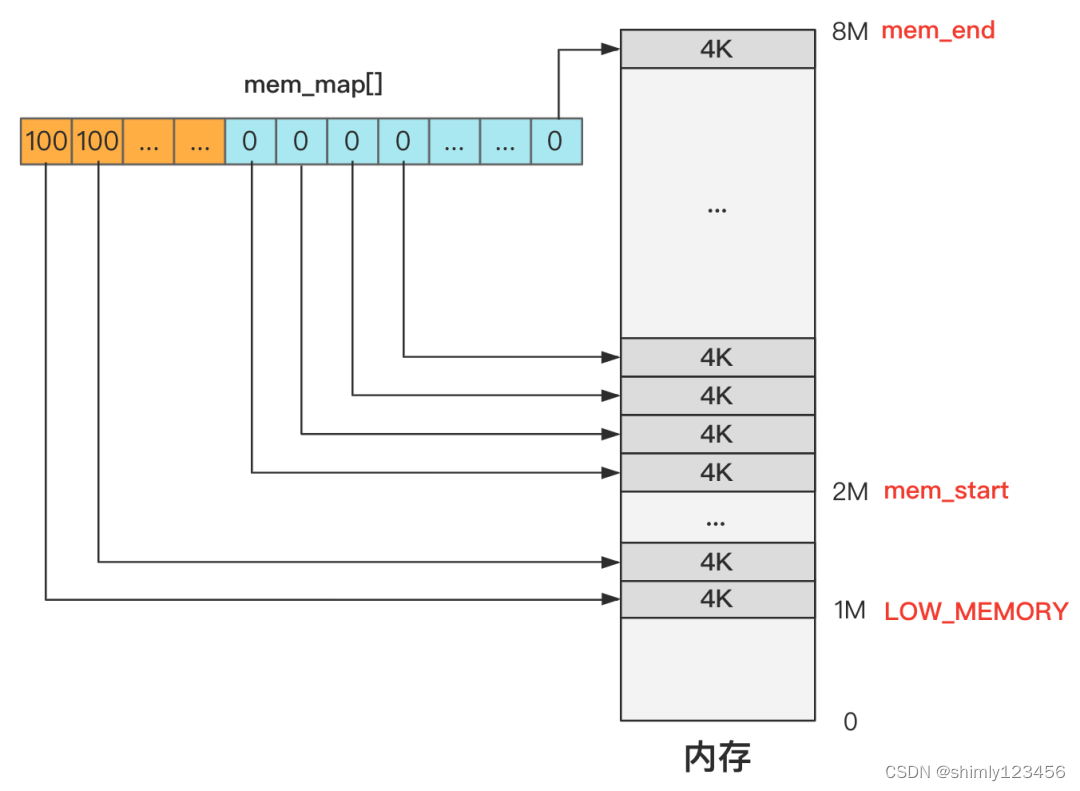
抄写Linux源码(Day16:内存管理)
回忆我们需要做的事情: 为了支持 shell 程序的执行,我们需要提供: 1.缺页中断(不理解为什么要这个东西,只是闪客说需要,后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的,所以需要这两个东…...

Cookie和Session详解以及结合生成登录效果
目录 引言 1.Cookie中的数据从哪来数据长啥样? 2.Cookie有什么作用? 3.cookie与session的工作关联? 4.Cookie到哪去? 5.Cookie如何存? 6.Session 7.Cookie与Session的关联与区别 8.通过代码理解 8.1 相关代码 8.2…...
Spring基础以及核心概念(IoC和DIQ)
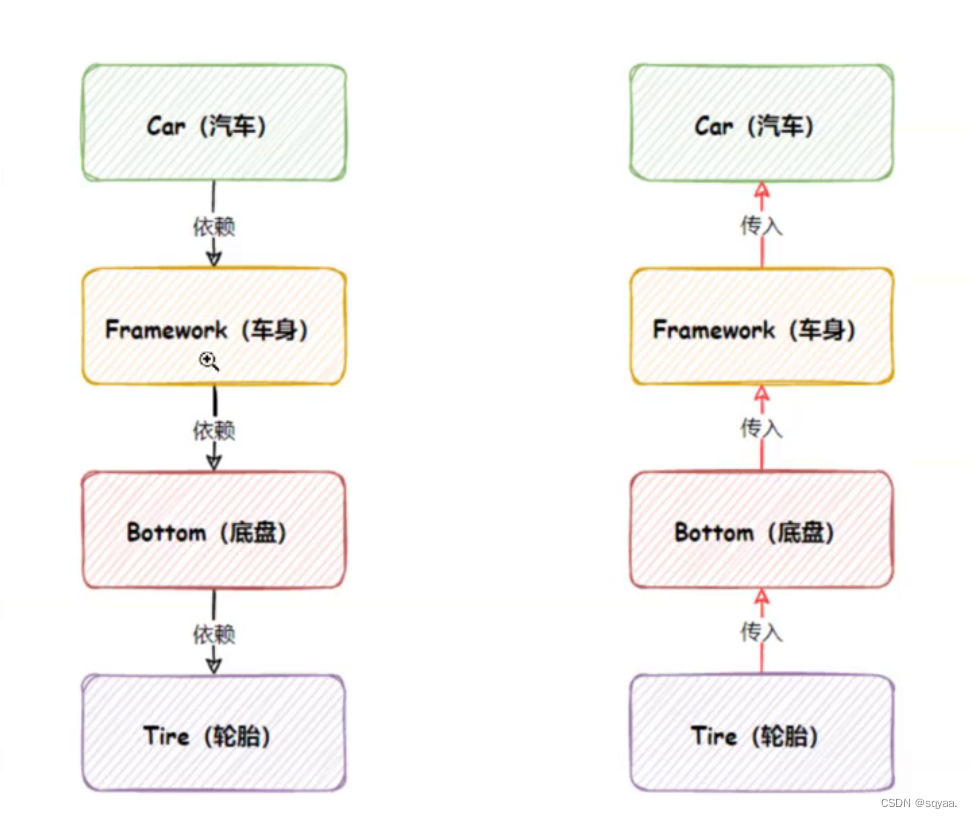
1.Spring是什么 Spring是包含了众多工具方法的IoC容器 2.loC(Inversion of Control )是什么 IoC:控制反转,Spring是一个控制反转容器(控制反转对象的生命周期) Spring是一个loC容器,我们之前学过的List/Map就是数据存储的容器,to…...

《C和指针》笔记32:多维数组初始化
文章目录 使用括号进行初始化初始化省略维度 使用括号进行初始化 我们可以给数组赋值一个长长的列表: int matrix[2][3] { 100, 101, 102, 110, 111, 112 };它等价于 matrix[0][0]100; matrix[0][1]101; matrix[0][2]102; matrix[1][0]110; matrix[1][1]111; ma…...
零食食品经营小程序商城的作用是什么
零食几乎可以涵盖每个年龄阶段,同时又是市场中常见的零售批发商品,在多个场景中都有销售/购买属性,对消费者来说,购买零食的渠道多种多样,无论线下还是线上,都可随心而购。 庞大市场升级促进下,…...

Java泛型--什么是泛型?
https://www.bilibili.com/video/BV1xJ411n77R?p5&vd_sourcebb1fced25254581cf052adea5e87a1ff 1.泛型类、接口 1.1.泛型类 泛型类的定义 class 类名称 <泛型标识, 泛型标识, ...> {private 泛型标识 变量名;...... }常用的泛型标识:T、E、K、V jav…...
LabVIEW工业虚拟仪器的标准化实施
LabVIEW工业虚拟仪器的标准化实施 创建计算机化的测试和测量系统,从计算机桌面控制外部测量硬件设备,以及在计算机屏幕上显示的类似仪器的面板上查看来自外部设备的测试或测量数据,所有这些都需要虚拟仪器系统软件。该软件允许用户执行所有这…...

JavaScript系列从入门到精通系列第十七篇:JavaScript中的全局作用域
文章目录 前言 1:什么叫作用域 一:全局作用域 1:全局变量的声明 2:变量声明和使用的顺序 3:方法声明和使用的顺序 前言 1:什么叫作用域 可以起作用的范围 function fun(){var a 1; } fun();consol…...

汇编指令集合
...
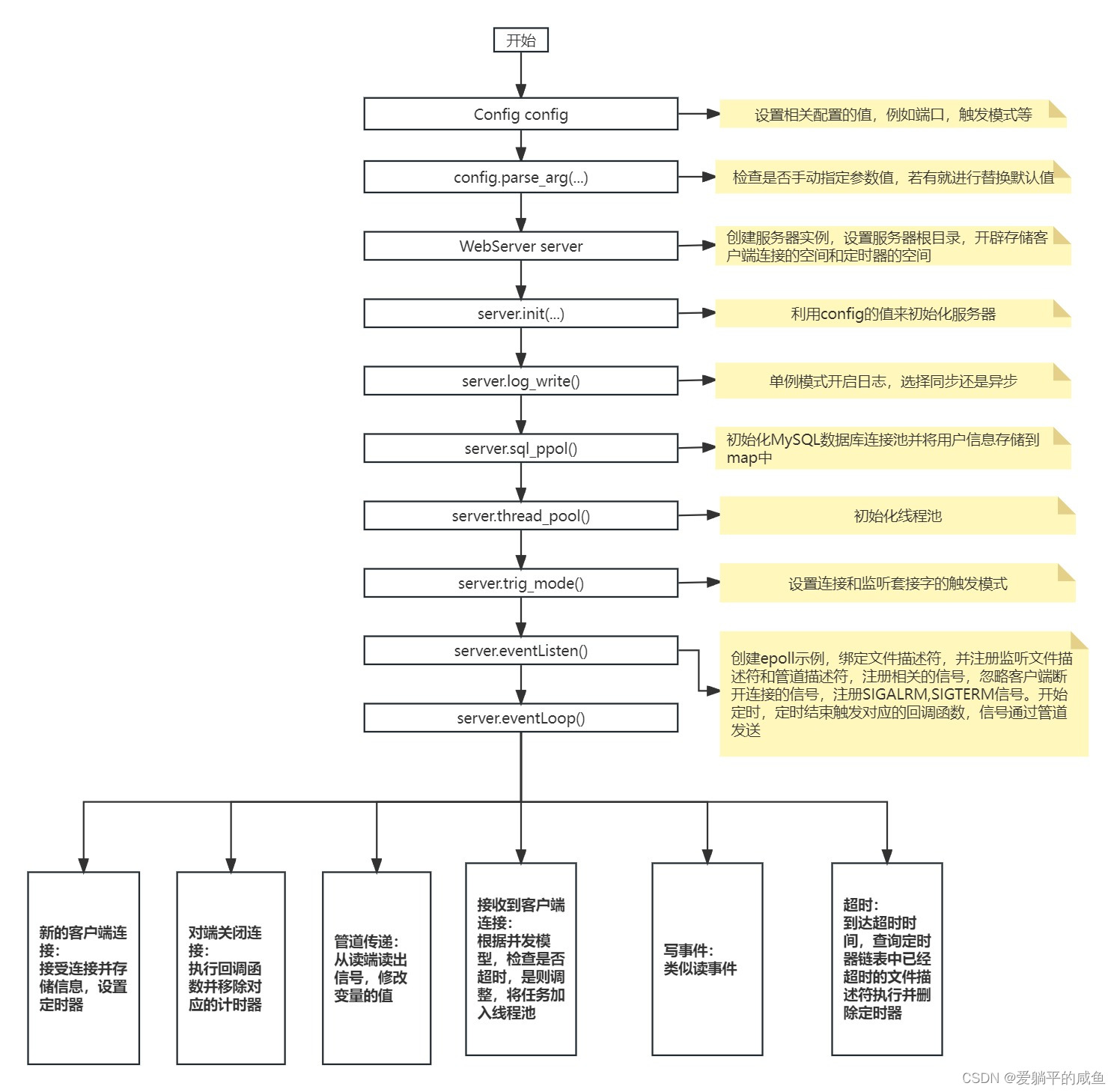
TinyWebServer整体流程
从main主函数开始: 一、定义MySQL数据库的账号、密码和用到的数据库名称。 二、调用Config获得服务器初始化属性 在这一步确定触发模式端口等信息。 三、创建服务器实例对象 设置根目录、开辟存放http连接对象的空间,开辟定时器空间。 四、利用Confi…...

【Java项目推荐之黑马头条】自媒体文章实现异步上下架(使用Kafka中间件实现)
自媒体文章上下架功能完成 需求分析 流程说明 接口定义 说明接口路径/api/v1/news/down_or_up请求方式POST参数DTO响应结果ResponseResult DTO Data public class WmNewsDto {private Integer id;/*** 是否上架 0 下架 1 上架*/private Short enable;}ResponseResult 自媒…...

自学(黑客)技术方法————网络安全
如果你想自学网络安全,首先你必须了解什么是网络安全!,什么是黑客!! 1.无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面性,例如 Web 安全技术,既有 Web 渗透2.也有 Web 防…...

python+playwright 学习-84 Response 接口返回对象
Response 是获取接口响应对象,根据Response 对象可以获取响应的状态码,响应头部,响应正文等内容。 Response 相关操作方法 all_headers 所有响应HTTP标头, 返回Dict 类型 response.all_headers()body 获取 bytes 类型body内容 response.body()json 返回响应主体的 JS…...

GCN详解
a ⃗ \vec{a} a 向量 a ‾ \overline{a} a 平均值 a ‾ \underline{a} a下横线 a ^ \widehat{a} a (线性回归,直线方程) y尖 a ~ \widetilde{a} a a ˙ \dot{a} a˙ 一阶导数 a \ddot{a} a 二阶导数 H(l)表示l层的节点的特征 W(l)表示l层的参数 D ~ \widet…...
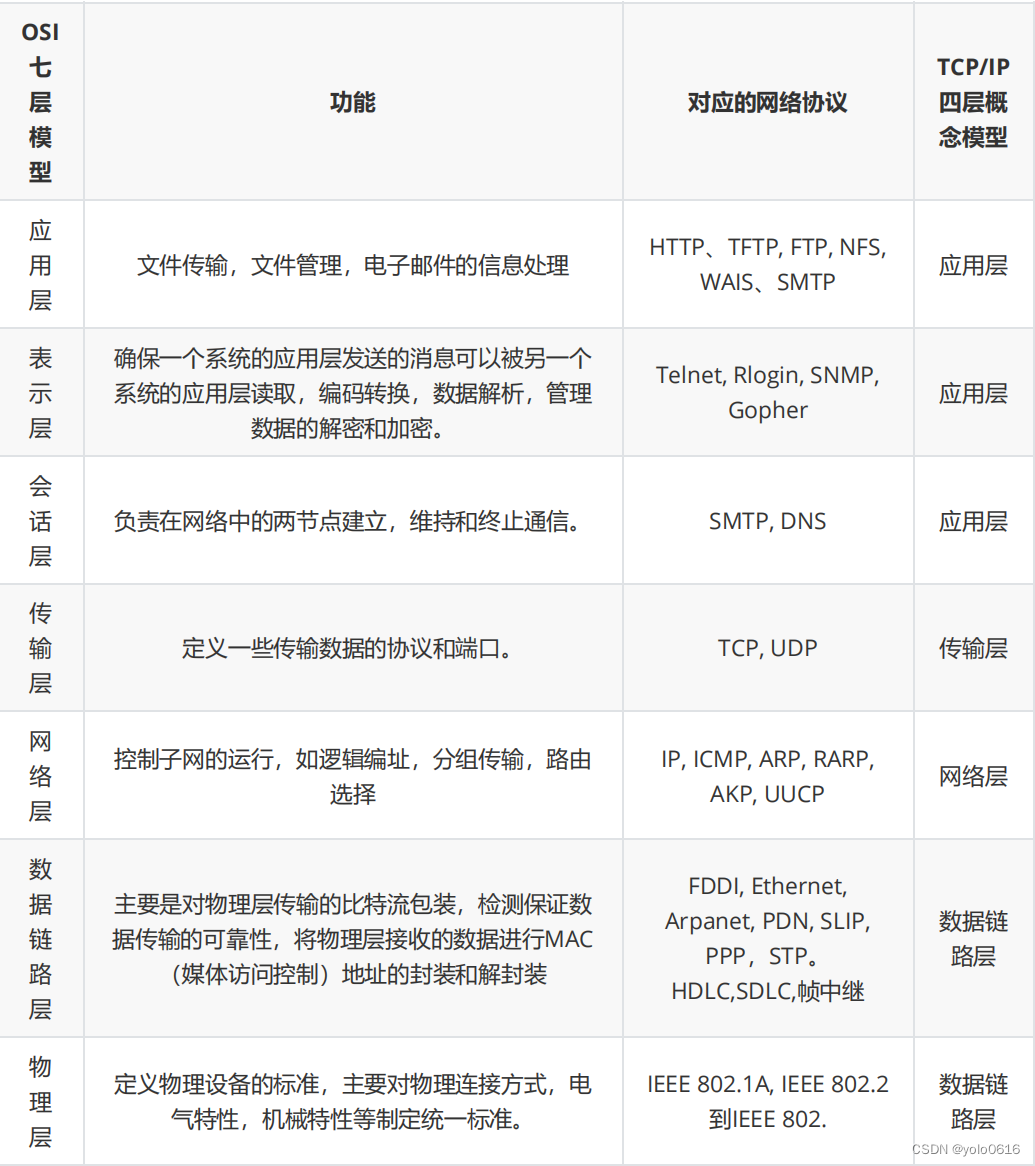
总结二:linux面经
文章目录 1、 Linux中查看进程运行状态的指令、查看内存使用情况的指令、tar解压文件的参数。2、文件权限怎么修改?3、说说常用的Linux命令?4、说说如何以root权限运行某个程序?5、 说说软链接和硬链接的区别?6、说说静态库和动态…...

12、【Qlib】【主要组件】Qlib Recorder:实验管理
11、【Qlib】【主要组件】Qlib Recorder:实验管理 简介Qlib RecorderExperiment ManagerExperimentRecorderRecord Template简介 Qlib包含一个名为QlibRecorder的实验管理系统,旨在帮助用户以高效的方式处理实验并分析结果。 该系统有三个组件: 实验管理器(ExperimentMan…...

三一充填泵:煤矿矸石无害化充填,煤炭绿色高效开采的破局利器
富煤贫油少气是我国的能源禀赋特征,决定了我国以煤炭为主的能源结构,煤炭为国民经济发展提供了重要的基础。煤炭开采过程会对土地、地下水、空气等环境造成较大的污染,但大宗固废煤矸石无害化充填的技术手段可以有效改善这样的情况࿰…...
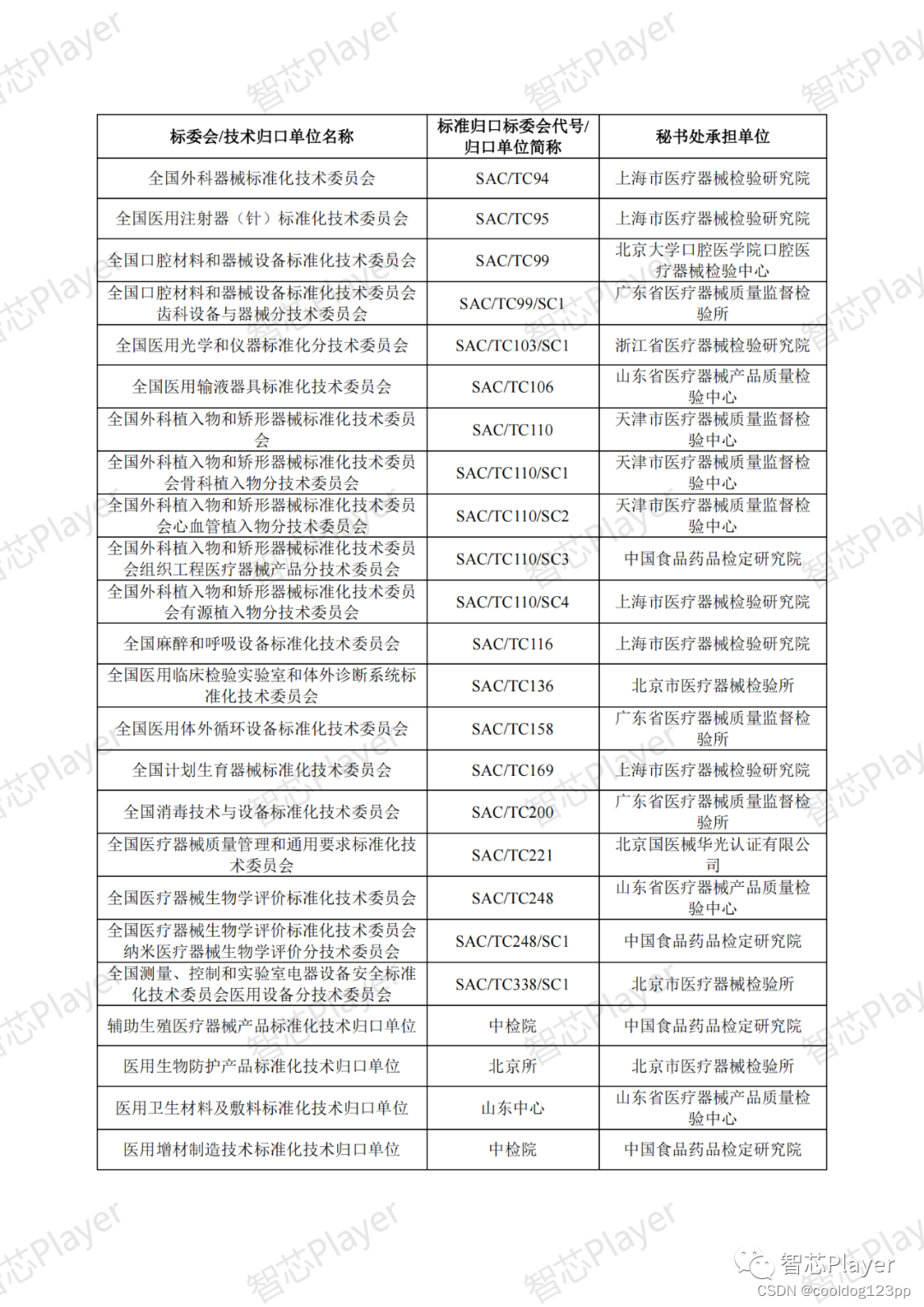
医疗器械标准目录汇编2022版共178页(文中附下载链接!)
为便于更好地应用医疗器械标准,国家药监局医疗器械标准管理中心组织对现行1851项医疗器械国家和行业标准按技术领域,编排形成《医疗器械标准目录汇编(2022版)》 该目录汇编分为通用技术领域和专业技术领域两大类,通用…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
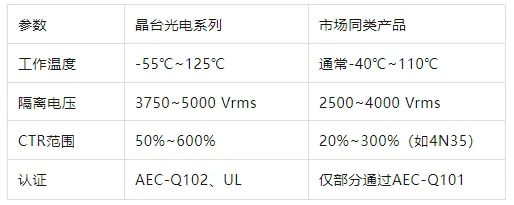
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
