折半+dp之限制转状态+状压:CF1767E
https://vjudge.net/problem/CodeForces-1767E/origin
首先40,必然折半。然后怎么做?
分析性质。每次可以走1步or2步,等价什么?等价任意相邻2个必选一个!然后就可以建图
这个图是个限制图,我们折半后可以进行状压。dp的过程是限制转状态。
首先分别的,前后内部都必须满足。然后对于交织在两部分的限制,我们枚举其中一边哪些不选,必然可以对应另外那边哪些必选。得到的集合求其最小合法超集即是答案。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 300010
#define M 21
//#define mo
int n, m, i, j, k, T;
int ans, f[1<<M], b[M<<1][M<<1];
int a[N], s, t, mid, cost[M<<1];
int k1, k2, s1, s2; void cun(int x, int y) {b[x][y]=b[y][x]=1;
}int check(int s) {if(k1<mid && (s&s1)==0) return 0; if(k2<mid && (s&s2)==0) return 0; for(int i=0; i<mid; ++i)for(int j=0; j<mid; ++j)if(b[i][j] && (!(s&(1<<i)) && !(s&(1<<j)))) return 0; return 1;
}int check2(int s) {if(k1>=mid && (s&s1)==0) return 0; if(k2>=mid && (s&s2)==0) return 0; for(int i=mid; i<m; ++i)for(int j=mid; j<m; ++j) if(b[i][j] && (!(s&(1<<i-mid)) && !(s&(1<<j-mid)))) return 0; return 1;
}void Least(int s, int &t) {for(int i=mid; i<m; ++i)for(int j=0; j<mid; ++j) {
// printf("(%d %d) %d\n", i, j); if(b[i][j] && !(s&(1<<i-mid))) t|=(1<<j); }}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); m=read(); mid=m/2; ans=1e18;
// printf("%lld\n", mid); for(i=1; i<=n; ++i) a[i]=read()-1; s1=(1<<a[1]); s2=(1<<a[n]); k1=a[1]; k2=a[n]; if(k1>=mid) s1=(1<<a[1]-mid); if(k2>=mid) s2=(1<<a[n]-mid);
// printf("%d %d | %d %d\n", k1, k2, s1, s2); for(i=1; i<n; ++i) cun(a[i], a[i+1]); for(i=0; i<m; ++i) cost[i]=read(); memset(f, 0x3f, sizeof(f)); for(s=(1<<mid)-1; s>=0; --s) {if(check(s)) {
// printf("> %d ", s); for(i=k=0; i<mid; ++i) if(s&(1<<i)) k+=cost[i];
// printf("%lld\n", k); f[s]=min(f[s], k); }for(i=0; i<mid; ++i) if(s&(1<<i))f[s-(1<<i)]=min(f[s-(1<<i)], f[s]); }for(s=0; s<(1<<m-mid); ++s) {if(check2(s)) {
// printf(">> %d ", s);t=0; Least(s, t); for(i=k=0; i<m-mid; ++i) if(s&(1<<i)) k+=cost[i+mid];
// printf("%lld %lld\n", k, t); ans=min(ans, k+f[t]); }}printf("%lld", ans); return 0;
}相关文章:

折半+dp之限制转状态+状压:CF1767E
https://vjudge.net/problem/CodeForces-1767E/origin 首先40,必然折半。然后怎么做? 分析性质。每次可以走1步or2步,等价什么?等价任意相邻2个必选一个!然后就可以建图 这个图是个限制图,我们折半后可以…...

如何写出优质代码
(本文转载自其他博主但是个人忘记了出处) 优质代码是什么? 优质代码是指那些易于理解、易于维护、可读性强、结构清晰、没有冗余、运行效率高、可复用性强、稳定性好、可扩展性强的代码。 这类代码不仅能够准确执行预期功能,同时也便于其他开发者理解…...
ChatGLM2-6B的通透解析:从FlashAttention、Multi-Query Attention到GLM2的微调、源码解读
前言 本文最初和第一代ChatGLM-6B的内容汇总在一块,但为了阐述清楚FlashAttention、Multi-Query Attention等相关的原理,以及GLM2的微调、源码解读等内容,导致之前那篇文章越写越长,故特把ChatGLM2相关的内容独立抽取出来成本文 …...
3D人脸生成的论文
一、TECA 1、论文信息 2、开源情况:comming soon TECA: Text-Guided Generation and Editing of Compositional 3D AvatarsGiven a text description, our method produces a compositional 3D avatar consisting of a mesh-based face and body and NeRF-based ha…...

解决问题:可以用什么方式实现自动化部署
自动化部署可以使用多种工具来实现: 脚本编写:可以使用 Bash、Python 等编写脚本来实现自动化部署。例如,可以使用 Bash 脚本来自动安装、配置和启动应用程序。 配置管理工具:像 Ansible、Puppet、Chef、Salt 等配置管理工具可以…...

【数据结构】链表栈
目录: 链表栈 1. 链式栈的实现2. 链表栈的创建3. 压栈4. 弹栈 链表栈 栈的主要表示方式有两种,一种是顺序表示,另一种是链式表示。本文主要介绍链式表示的栈。 链栈实际上和单链表差别不大,唯一区别就在于只需要对链表限定从头…...

Android笔记:Android 组件化方案探索与思考
组件化项目,通过gradle脚本,实现module在编译期隔离,运行期按需加载,实现组件间解耦,高效单独调试。 先来一张效果图 组件化初衷 APP版本不断的迭代,新功能的不断增加,业务也会变的越来越复杂…...
MeterSphere v2.10.X-lts 双节点HA部署方案
一、MeterSphere高可用部署架构及服务器配置 1.1 服务器信息 序号应用名称操作系统要求配置要求描述1负载均衡器CentOS 7.X /RedHat 7.X2C,4G,200GB部署Nginx,实现负载路由。 部署NFS服务器。2MeterSphere应用节点1CentOS 7.X /RedHat 7.X8C,16GB,200G…...
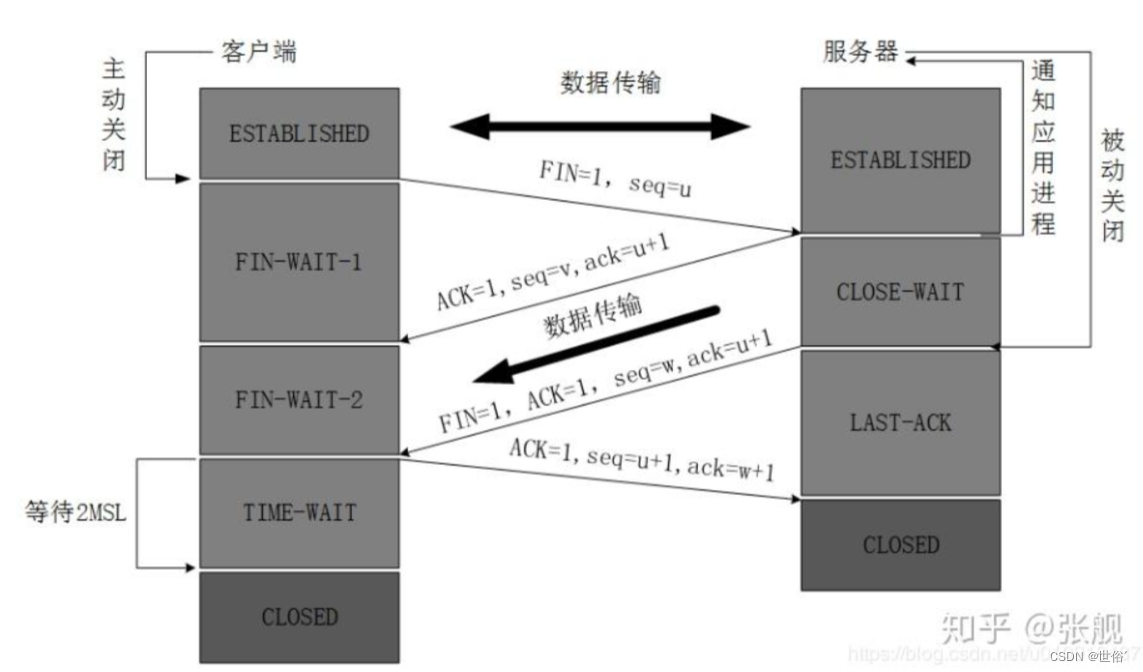
Java进阶篇--网络编程
目录 计算机网络体系结构 什么是网络协议? 为什么要对网络协议分层? 网络通信协议 TCP/IP 协议族 应用层 运输层 网络层 数据链路层 物理层 TCP/IP 协议族 TCP的三次握手四次挥手 TCP报文的头部结构 三次握手 四次挥手 …...

PyTorch入门之【CNN】
参考:https://www.bilibili.com/video/BV1114y1d79e/?spm_id_from333.999.0.0&vd_source98d31d5c9db8c0021988f2c2c25a9620 书接上回的MLP故本章就不详细解释了 目录 traintest train import torch from torchvision.transforms import ToTensor from torchvi…...

马斯洛需求层次模型之安全需求之云安全浅谈
在互联网云服务领域,安全需求是用户首要考虑的因素之一。用户希望在将数据和信息托付给云服务提供商时,这些数据和信息能够得到充分的保护,避免遭受未经授权的访问、泄露或破坏。这种安全需求的满足,对于用户来说是至关重要的&…...
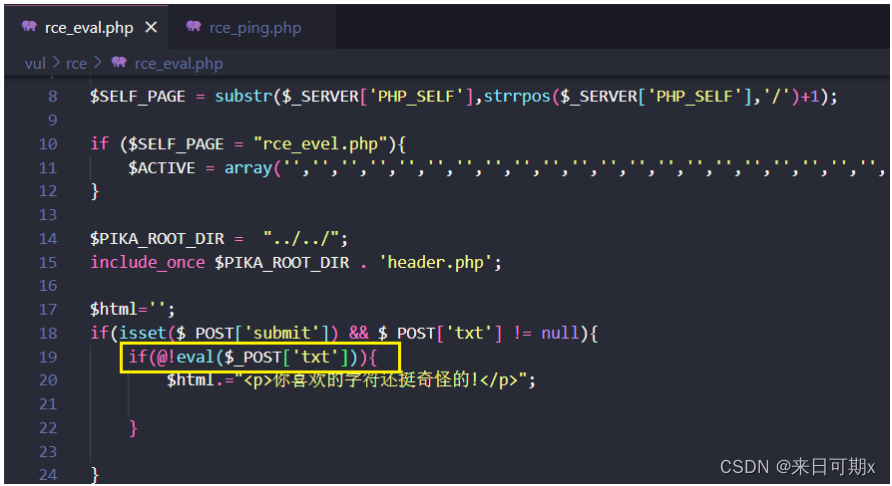
Pikachu靶场——远程命令执行漏洞(RCE)
文章目录 1. RCE1.1 exec "ping"1.1.1 源代码分析1.1.2 漏洞防御 1.2 exec "eval"1.2.1 源代码分析1.2.2 漏洞防御 1.3 RCE 漏洞防御 1. RCE RCE(remote command/code execute)概述: RCE漏洞,可以让攻击者直接向后台服务器远程注入…...
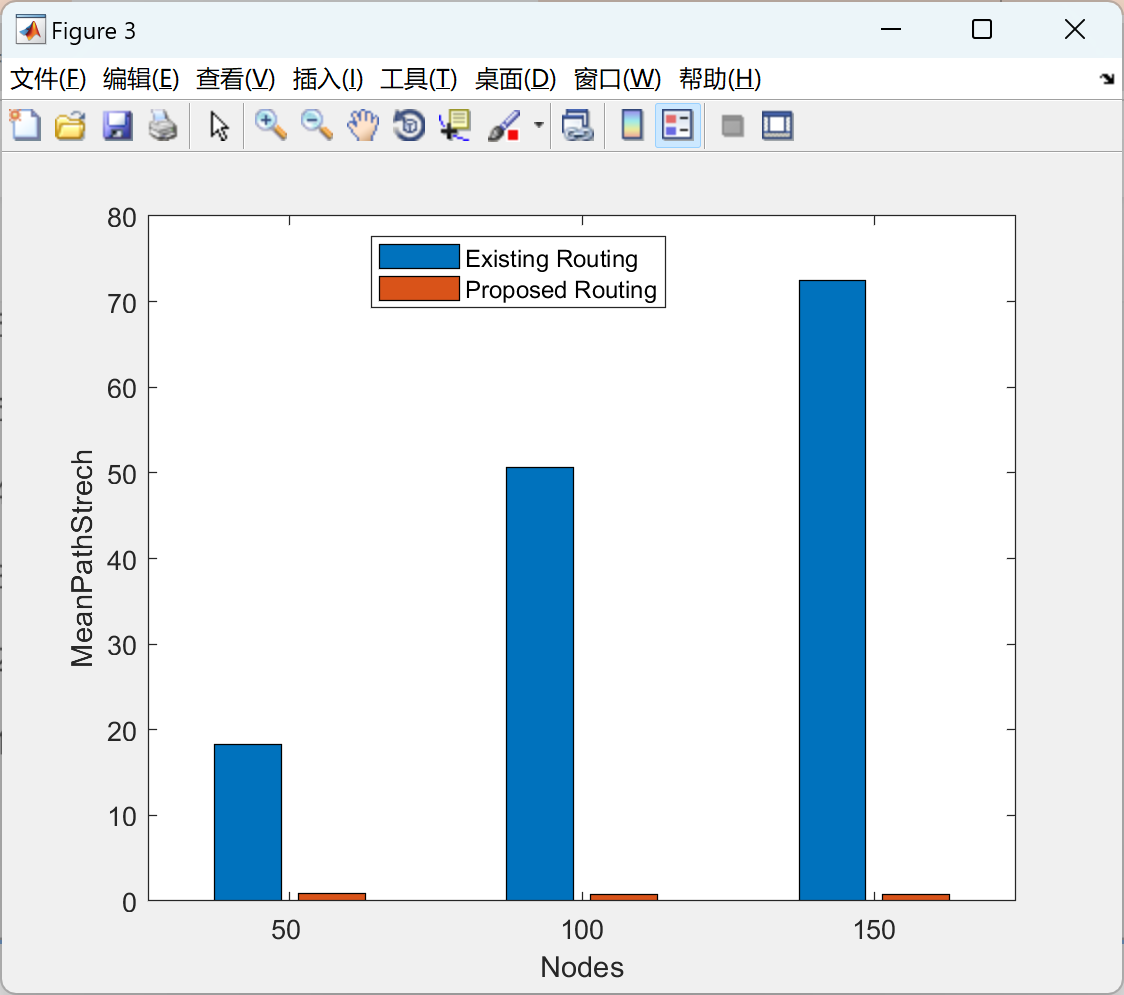
【WSN】无线传感器网络 X-Y 坐标到图形视图和位字符串前缀嵌入方法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux定时任务
文章目录 前言设置定时任务流程定时规则例子 终止定时任务列出当前的定时任务重启任务调度 前言 在Linux系统中有时侯需要周期性的自动执行一些命令,这时候Linux定时任务就派上用场了 设置定时任务流程 进入定时任务的编辑模式 crontab -e编辑定时任务ÿ…...
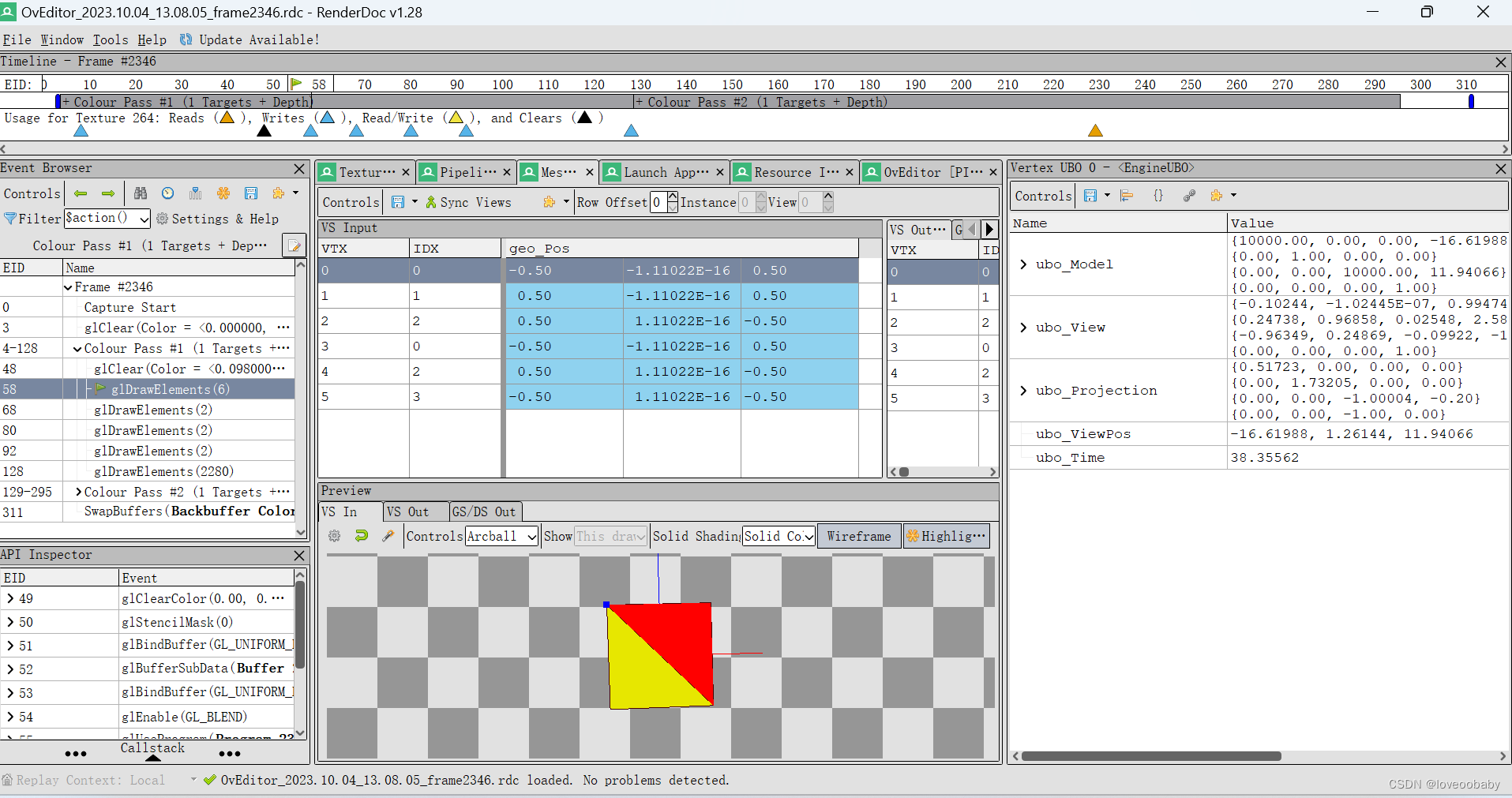
【Overload游戏引擎分析】画场景网格的Shader
Overload引擎地址: GitHub - adriengivry/Overload: 3D Game engine with editor 一、栅格绘制基本原理 Overload Editor启动之后,场景视图中有栅格线,这个在很多软件中都有。刚开始我猜测它应该是通过绘制线实现的。阅读代码发现࿰…...

【JavaEE】多线程进阶(一)饿汉模式和懒汉模式
多线程进阶(一) 文章目录 多线程进阶(一)单例模式饿汉模式懒汉模式 本篇主要引入多线程进阶的单例模式,为后面的大冰山做铺垫 代码案例介绍 单例模式 非常经典的设计模式 啥是设计模式 设计模式好比象棋中的 “棋谱”…...
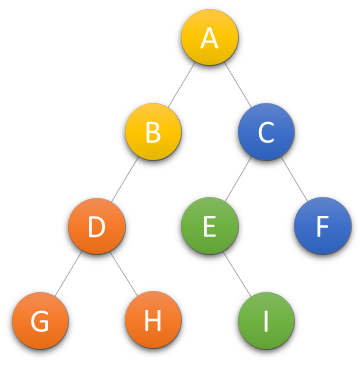
C++树详解
树 树的定义 树(Tree)是n(n≥0)个结点的有限集。n0时称为空树。在任意一颗非空树中:①有且仅有一个特定的称为根(Root)的结点;②当n>1时,其余结点可分为m(…...

支付环境安全漏洞介绍
1、平台支付逻辑全流程分析 2、平台支付漏洞如何利用?买东西还送钱? 3、BURP抓包分析修改支付金额,伪造交易状态? 4、修改购物车参数实现底价购买商品 5、SRC、CTF、HW项目月入10W副业之路 6、如何构建最适合自己的网安学习路线 1…...
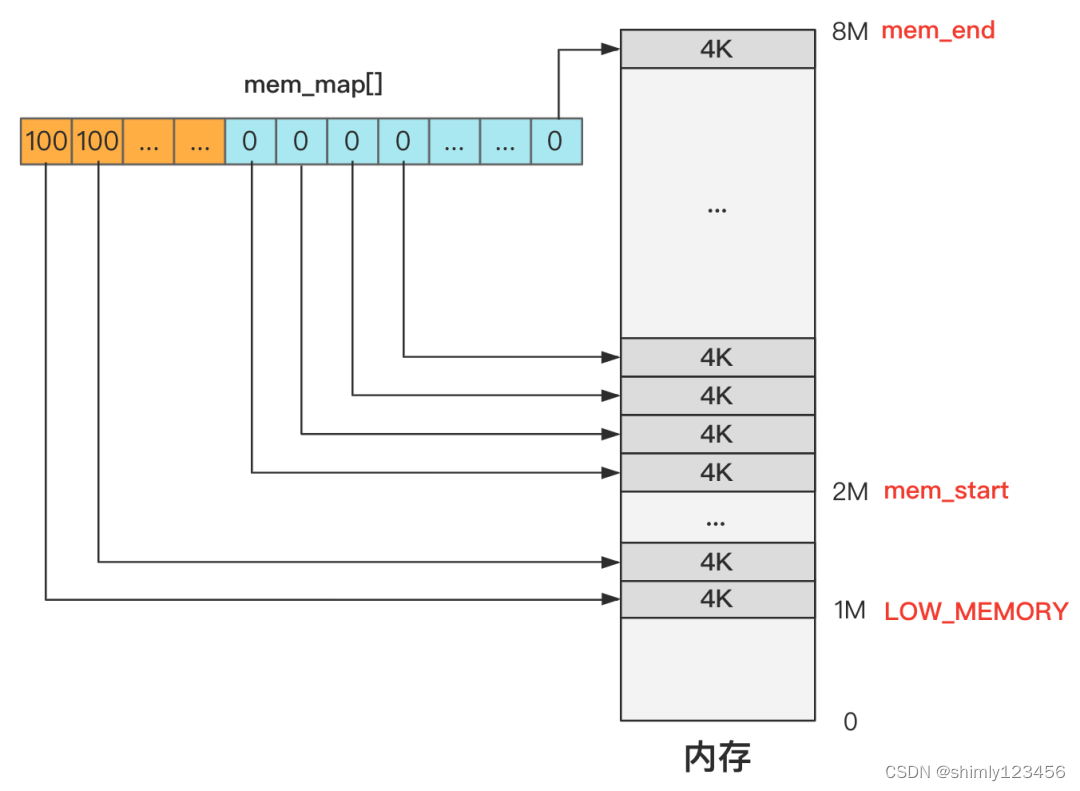
抄写Linux源码(Day16:内存管理)
回忆我们需要做的事情: 为了支持 shell 程序的执行,我们需要提供: 1.缺页中断(不理解为什么要这个东西,只是闪客说需要,后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的,所以需要这两个东…...

Cookie和Session详解以及结合生成登录效果
目录 引言 1.Cookie中的数据从哪来数据长啥样? 2.Cookie有什么作用? 3.cookie与session的工作关联? 4.Cookie到哪去? 5.Cookie如何存? 6.Session 7.Cookie与Session的关联与区别 8.通过代码理解 8.1 相关代码 8.2…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
