《算法通关之路》chapter19解题技巧和面试技巧
《算法通关之路》学习笔记,记录一下自己的刷题过程,详细的内容请大家购买作者的书籍查阅。
1 看限制条件
1.1数据规模
有的题目数据规模较小,那么暴力法就可行;如果暴力法不行,那么再稍微加一个诸如缓存和剪枝的优化一般可以通过。
根据题目所给的数据规模,就大概锁定了能够选择的算法。
≤ 1 0 6 10^{6} 106可接受的复杂度O(nlogn)
≤ 1 0 7 10^{7} 107可接受的复杂度O(n)
转化为全零矩阵的最少反转次数
力扣第1284题
给你一个 m x n 的二进制矩阵 mat。每一步,你可以选择一个单元格并将它反转(反转表示 0 变 1 ,1 变 0 )。如果存在和它相邻的单元格,那么这些相邻的单元格也会被反转。相邻的两个单元格共享同一条边。
请你返回将矩阵 mat 转化为全零矩阵的最少反转次数,如果无法转化为全零矩阵,请返回 -1 。
二进制矩阵 的每一个格子要么是 0 要么是 1 。
全零矩阵 是所有格子都为 0 的矩阵。
1 <= m <= 3
1 <= n <= 3
'''
方法一:广度优先遍历(降维)时间复杂度:O(2^{mn})
空间复杂度:O(2^{mn})
'''class Solution:def minFlips(self, mat: list[list[int]]) -> int:# 放到flip函数外部可以减少计算mapper = {'0': '1', '1': '0'}def flip(state: list[str], i: int) -> None:state[i] = mapper[state[i]]if i % n != 0:state[i - 1] = mapper[state[i - 1]]if i % n < n - 1:state[i + 1] = mapper[state[i + 1]]if i >= n:state[i - n] = mapper[state[i - n]]if i < (m - 1) * n:state[i + n] = mapper[state[i + n]]m, n = len(mat), len(mat[0])target = '0' * (m * n)cur = ''.join(str(cell) for row in mat for cell in row)queue = [cur]visited = set()steps = 0while len(queue) > 0:for _ in range(len(queue)):cur = queue.pop(0)if cur == target:return stepsif cur in visited:continuevisited.add(cur)for i in range(len(cur)):s = list(cur)flip(s, i)queue.append(''.join(s))steps += 1return -1mat = [[0,0],[0,1]]
solu = Solution()
solu.minFlips(mat)
3
1.2 复杂度
题目要求时间复杂度是对数复杂度,就很容易想到二分查找。
题目要求常数的空间复杂度,就很容易想到原地算法。
题目中出现有序,应该联想到双指针、二分法等有序序列算法。
题目中出现连续子数组或连续子串,我们应该联想到滑动窗口。
矩阵置零
力扣第73题
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
'''
方法一:原地算法时间复杂度:O(mn)
空间复杂度:O(1)
'''class Solution:def setZeroes(self, matrix: list[list[int]]) -> None:C = len(matrix[0])R = len(matrix)def setRowZeros(matrix: list[list[int]], i: int) -> None:matrix[i] = [0] * Cdef setColZeros(matrix: list[list[int]], j: int) -> None:for i in range(R):matrix[i][j] = 0isCol = False # 如果不使用一个变量来存第一行或者第一列,最后矩阵会都变为0for i in range(R):if matrix[i][0] == 0:isCol = Truefor j in range(1, C):if matrix[i][j] == 0:matrix[i][0] = 0matrix[0][j] = 0for j in range(1, C): # 第一列存着行的变换if matrix[0][j] == 0:setColZeros(matrix, j)for i in range(R):if matrix[i][0] == 0:setRowZeros(matrix, i)if isCol:setColZeros(matrix, 0)matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
solu = Solution()
solu.setZeroes(matrix)
print(matrix)
[[0, 0, 0, 0], [0, 4, 5, 0], [0, 3, 1, 0]]
2 预处理
提前将计算结果存起来,在实际的计算过程中直接使用,从而节省计算资源。虽然打表是空间换时间,但是其空间并不随着数据规模增大而增大,很多情况下都是值得的。
顺次数
力扣第1291题
我们定义「顺次数」为:每一位上的数字都比前一位上的数字大 1 的整数。
请你返回由 [low, high] 范围内所有顺次数组成的 有序 列表(从小到大排序)。
10 <= low <= high <= 10^9
'''
方法一:打表时间复杂度:O(1)
空间复杂度:O(1)
'''class Solution:def sequentialDigits(self, low: int, high: int) -> list[int]:numbers = '123456789'ins = []n = len(numbers)for i in range(1, n): # i控制长度for j in range(n - i): # j控制位置ins.append(int(numbers[j : i + j + 1]))return [x for x in ins if x >= low and x <= high]low, high = 1000, 13000
solu = Solution()
solu.sequentialDigits(low, high)
[1234, 2345, 3456, 4567, 5678, 6789, 12345]
'''
方法二:打表 + 二分查找时间复杂度:O(1)
空间复杂度:O(1)
'''import bisectclass Solution:def sequentialDigits(self, low: int, high: int) -> list[int]:numbers = '123456789'ins = []n = len(numbers)for i in range(1, n): # i控制长度for j in range(n - i): # j控制位置ins.append(int(numbers[j : i + j + 1]))return ins[bisect.bisect_left(ins, low) : bisect.bisect(ins, high)]low, high = 1000, 13000
solu = Solution()
solu.sequentialDigits(low, high)
[1234, 2345, 3456, 4567, 5678, 6789, 12345]
'''
方法三:最朴实的打表时间复杂度:O(1)
空间复杂度:O(1)
'''import bisectclass Solution:def sequentialDigits(self, low: int, high: int) -> list[int]:ins = [12, 23, 34, 45, 56, 67, 78, 89, 123, 234, 345, 456, 567, 678, 789, 1234, 2345, 3456, 4567, 5678, 6789, 12345, 23456, 34567, 45678, 56789, 123456, 234567, 345678, 456789, 1234567, 2345678, 3456789, 12345678, 23456789, 123456789]return ins[bisect.bisect_left(ins, low) : bisect.bisect(ins, high)]low, high = 1000, 13000
solu = Solution()
solu.sequentialDigits(low, high)
[1234, 2345, 3456, 4567, 5678, 6789, 12345]
单词接龙
力扣第127题
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk:
每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
'''
方法一:暴力BFS(超时)时间复杂度:O(m^2*n)
空间复杂度:O(n)
'''class Solution:def ladderLength(self, beginWord: str, endWord: str, wordList: list[str]) -> int:queue = [beginWord]visited = set()steps = 1L = len(beginWord)while len(queue) > 0:for _ in range(len(queue)):cur = queue.pop(0)if cur in visited:continuevisited.add(cur)if cur == endWord:return stepsfor i in range(L):for j in range(26):s = list(cur)s[i] = chr(ord('a') + j) # ord()转换ASCII码,chr转换为字符for word in wordList:if word == ''.join(s):queue.append(word)steps += 1return 0beginWord, endWord, wordList = "hit", "cog", ["hot","dot","dog","lot","log","cog"]
solu = Solution()
solu.ladderLength(beginWord, endWord, wordList)
5
'''
方法二:预处理 + BFS (空间换时间)时间复杂度:O(m*n)
空间复杂度:O(m*n)
'''from collections import defaultdictclass Solution:def ladderLength(self, beginWord: str, endWord: str, wordList: list[str]) -> int:queue = [beginWord]visited = set()steps = 1L = len(beginWord)n = len(wordList)wizards = defaultdict(list)for i in range(n):word = wordList[i]for j in range(L):wizards[word[:j] + '*' + word[j + 1 : ]].append(word)print(wizards)while len(queue) > 0:for _ in range(len(queue)):cur = queue.pop(0)if cur in visited:continuevisited.add(cur)if cur == endWord:return stepsfor i in range(L):for word in wizards.get(cur[:i] + '*' + cur[i + 1 :], []):queue.append(word)steps += 1return 0beginWord, endWord, wordList = "hit", "cog", ["hot","dot","dog","lot","log","cog"]
solu = Solution()
solu.ladderLength(beginWord, endWord, wordList)
5
3 不要忽视暴力法
统计全为 1 的正方形子矩阵
力扣第1277题
给你一个 m * n 的矩阵,矩阵中的元素不是 0 就是 1,请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
'''
方法一:暴力法(超时)时间复杂度:O(m*n*min(m,n))
空间复杂度:O(1)
'''class Solution:def countSquares(self, matrix: list[list[int]]) -> int:num_rows, num_cols = len(matrix), len(matrix[0])min_side_length = min(num_rows, num_cols)def is_all_ones(matrix):for row in matrix:for element in row:if element != 1:return Falsereturn Truecnt = 0for side_length in range(1, min_side_length + 1):for i in range(num_rows - side_length + 1):for j in range(num_cols - side_length + 1):if is_all_ones([row[j : j + side_length] for row in matrix[i : i + side_length]]): # 遍历二维list中所有边长为side_length的正方形cnt += 1return cntmatrix = [[0,1,1,1],[1,1,1,1],[0,1,1,1]
]
solu = Solution()
solu.countSquares(matrix)
15
'''
方法二:动态规划时间复杂度:O(m*n)
空间复杂度:O(m*n)
'''class Solution:def countSquares(self, matrix: list[list[int]]) -> int:num_rows, num_cols = len(matrix), len(matrix[0])cnt = 0# dp[i][j]表示以顶点i,j为右下角所能构成的最大正方形边长dp = [[0] * (num_cols + 1) for _ in range(num_rows + 1)]for i in range(1, num_rows + 1):for j in range(1, num_cols + 1):if matrix[i - 1][j - 1] == 1:dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1cnt += dp[i][j]return cntmatrix = [[0,1,1,1],[1,1,1,1],[0,1,1,1]
]
solu = Solution()
solu.countSquares(matrix)
15
子串的最大出现次数
力扣第1297题
给你一个字符串 s ,请你返回满足以下条件且出现次数最大的 任意 子串的出现次数:
子串中不同字母的数目必须小于等于 maxLetters 。
子串的长度必须大于等于 minSize 且小于等于 maxSize 。
'''
方法一:暴力法时间复杂度:O((26^2)*n)
空间复杂度:O((26^2)*n)
'''class Solution:def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:counter = {}for i in range(0, len(s) - minSize + 1): # 记住这种写法for length in range(minSize, maxSize + 1):if i + length > len(s):breaksub = s[i : i + length]if len(set(sub)) <= maxLetters: # 用set统计不同字符数目counter[sub] = counter.get(sub, 0) + 1return max(counter.values()) if counter else 0s, maxLetters, minSize, maxSize = "aababcaab", 2, 3, 4
solu = Solution()
solu.maxFreq(s, maxLetters, minSize, maxSize)
2
'''
方法二:暴力法剪枝(只统计长度为minSize的子串即可)时间复杂度:O(26*n)
空间复杂度:O(26*n)
'''class Solution:def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:counter = {}for i in range(0, len(s) - minSize + 1):sub = s[i : i + minSize]if len(set(sub)) <= maxLetters:counter[sub] = counter.get(sub, 0) + 1return max(counter.values()) if counter else 0s, maxLetters, minSize, maxSize = "aababcaab", 2, 3, 4
solu = Solution()
solu.maxFreq(s, maxLetters, minSize, maxSize)
2
4 降维与状态压缩
# 判断一个字符串中的字符是否全部唯一(状态压缩)def isUnique(s: str) -> bool:seen = 0 # 相当于set()for c in s:if seen & 1 << ord(c) - ord('a') != 0: # 相当于判断c是否在set中return Falseseen |= 1 << ord(c) - ord('a') # 相当于将c加入setreturn TrueisUnique('absxssxsxsxsxsx')
False
生命游戏
力扣第289题
根据 百度百科 , 生命游戏 ,简称为 生命 ,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态,返回下一个状态。
'''
方法一:常规方法时间复杂度:O(mn)
空间复杂度:O(mn)
'''import copyclass Solution:def gameOfLife(self, board: list[list[int]]) -> None:"""Do not return anything, modify board in-place instead."""m, n = len(board), len(board[0])old = copy.deepcopy(board)def cntLiveCell(i: int, j: int) -> int:cnt = 0directions = [(0, 1),(0, -1),(-1, 0),(1, 0),(1, 1),(1, -1),(-1, 1),(-1, -1)]for (dx, dy) in directions:if i + dx >= 0 and i + dx < m and j + dy >= 0 and j + dy < n:cnt += old[i + dx][j + dy]return cntfor i in range(m):for j in range(n):cnt = cntLiveCell(i, j)if old[i][j] == 0 and cnt == 3:board[i][j] = 1if old[i][j] == 1 and (cnt < 2 or cnt > 3):board[i][j] = 0board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
solu = Solution()
solu.gameOfLife(board)
print(board)
[[0, 0, 0], [1, 0, 1], [0, 1, 1], [0, 1, 0]]
'''
方法二:状态压缩(将这个细胞中有多少活细胞这个信息存储到高位)时间复杂度:O(mn)
空间复杂度:O(1)
'''class Solution:def gameOfLife(self, board: list[list[int]]) -> None:"""Do not return anything, modify board in-place instead."""m, n = len(board), len(board[0])def cntLiveCell(i: int, j: int) -> int:cnt = 0directions = [(0, 1),(0, -1),(-1, 0),(1, 0),(1, 1),(1, -1),(-1, 1),(-1, -1)]for (dx, dy) in directions:if i + dx >= 0 and i + dx < m and j + dy >= 0 and j + dy < n:cnt += board[i + dx][j + dy] & 1return cntfor i in range(m):for j in range(n):cnt = cntLiveCell(i, j)board[i][j] |= cnt << 1for i in range(m):for j in range(n):cell = board[i][j] & 1cnt = board[i][j] >> 1if cell == 0 and cnt == 3:board[i][j] = 1elif cell == 1 and (cnt > 3 or cnt < 2):board[i][j] = 0else:board[i][j] = cellboard = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
solu = Solution()
solu.gameOfLife(board)
print(board)
[[0, 0, 0], [1, 0, 1], [0, 1, 1], [0, 1, 0]]
相关文章:

《算法通关之路》chapter19解题技巧和面试技巧
《算法通关之路》学习笔记,记录一下自己的刷题过程,详细的内容请大家购买作者的书籍查阅。 1 看限制条件 1.1数据规模 有的题目数据规模较小,那么暴力法就可行;如果暴力法不行,那么再稍微加一个诸如缓存和剪枝的优化…...
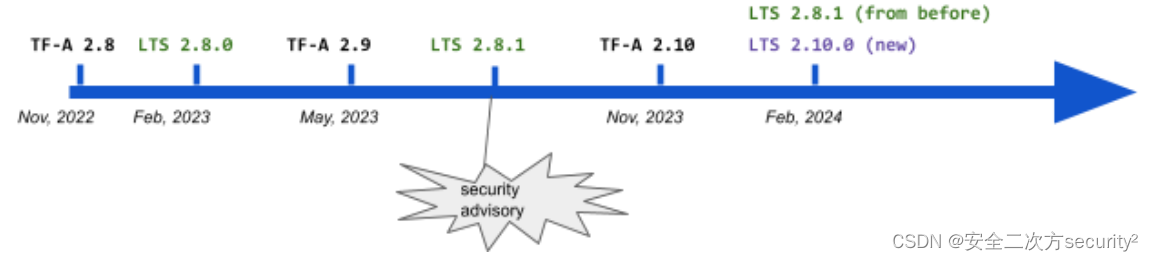
什么是TF-A项目的长期支持?
安全之安全(security)博客目录导读 问题:Trusted Firmware-A社区每六个月发布一次代码。然而,对于生产中的平台,该策略在维护、重要软件修复的向后兼容性、获得最新的安全缓解措施和整体产品生命周期管理方面不具备可扩展性。 开源软件项目&…...
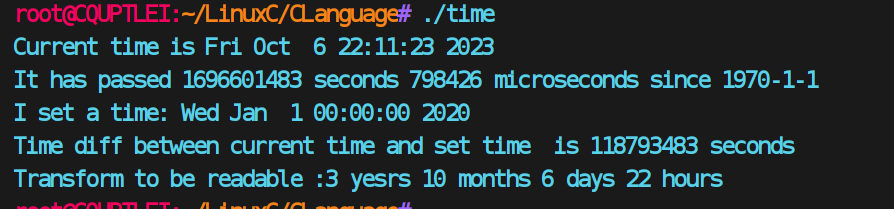
【LinuxC】时间、时区,相关命令、函数
文章目录 一、序1.1 时间和时区1.11 时间1.12 时区 1.2 查看时间时区的命令1.21 Windows1.22 Linux 二、C语言函数2.1 通用2.11 函数简介2.12 数据类型简介 2.2 windows 和 Linux特有函数2.3 C语言示例 一、序 1.1 时间和时区 1.11 时间 时间是一种用来描述物体运动变化的量…...
mac清理垃圾的软件有哪些?这三款我最推荐
没错,Mac电脑真的好用,但是清理系统垃圾可不是件容易的事。由于Mac系统的封闭性,系统的缓存垃圾常常隐藏得让人发现不了。不过,别担心!有一些专业的Mac清理软件可以帮你解决这一系列问题,让清理垃圾变得轻松…...
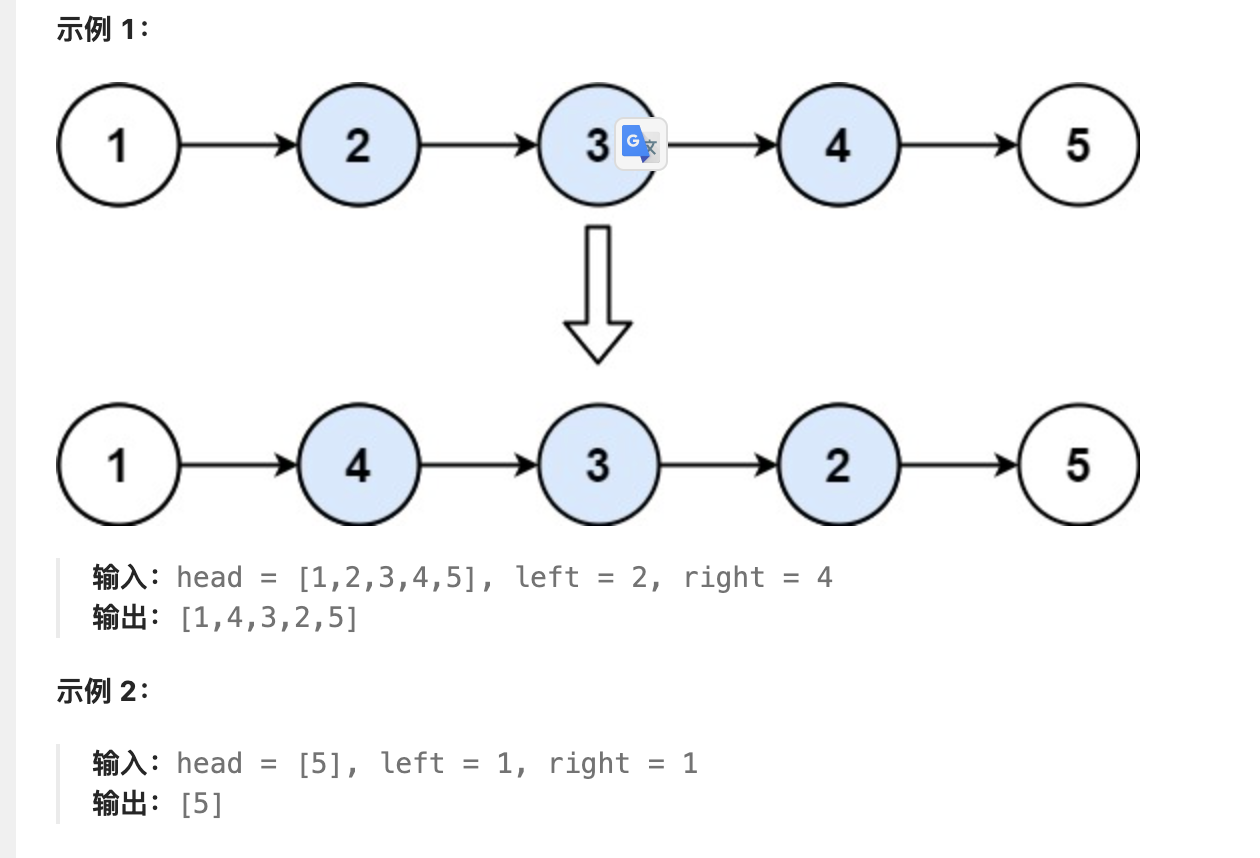
复习Day11:链表part04: 206. 反转链表、92. 反转链表II、25. K 个一组翻转链表、148. 排序链表
我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用CLion了,使用leetcode自带的IDE模拟面试环境。 哈希表章节的题目思路很清晰&…...
一年一度的国庆节又结束了
这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…...
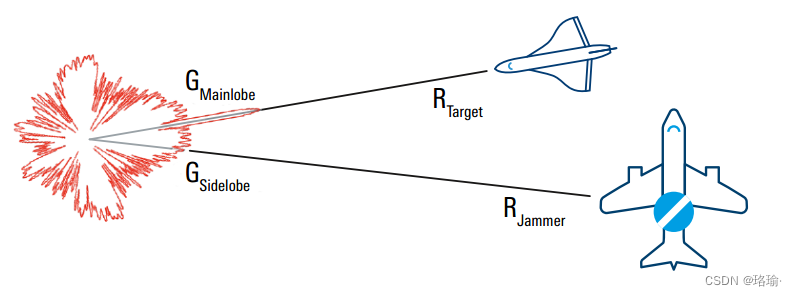
雷达干扰和烧穿范围简介
一、干扰信号比 J/S或J-to-S是从目标发射的干扰信号接收的功率(J)与从目标的雷达反向散射接收的功率的比率。 二、烧穿范围 通过电子攻击(J)可以首先检测到目标回波信号(S)的雷达到目标的距离。 三、自保护干扰 也称为主瓣干扰(雷达回波源和干扰机并置)。 烧穿范围…...

“秋天第一只大闸蟹”背后,看见京东一体化供应链
京东似乎正在从一个大闸蟹的物流服务商、销售商,转变为一个大闸蟹的“供货商”。 作者|斗斗 编辑|皮爷 出品|产业家 阳澄湖连续几天的降雨,使得通往蟹塘的路异常难走。 长期驻扎此地的京东相关负责人蹲在蟹塘边的小路上,指着蟹塘说道…...

大模型Java编码能力评估
大模型如火如荼发展,不能只看热闹,也需要躬身入局。要想评估大模型的能力,必须有一个评估方法和评估数据集。下面就梳理下当前大模型是如何评估代码能力的 权威评估 opencompass: https://opencompass.org.cn/datalearner: https://www.dat…...

javascript选择框和选择文本的创建与增加以及设置选中项
<script type"text/javascript">//得到选中项的索引,文本和值函数function getselected(selectedIndex){var selectboxdocument.forms[0].elements["location"];var indexselectbox[selectedIndex];var selectedOptionselectbox.options[…...

汽车驾驶任务的隐马尔可夫模型识别方法研究
汽车驾驶任务的隐马尔可夫模型识别方法研究 一、Introduction 自动驾驶汽车经过了几十年的发展,是目前国内外汽车行业中的重要研究方向。自 动驾驶汽车的智能化需要车辆能够有类“人”的行为,在决策策略上可以满足人的心理 需求。人在驾驶过程中&#…...

Java编程题(完数)
题目 一个正整数的因子是所有可以整除它的正整数。而一个数如果恰好等于除它本身外的因子之和,这个数就称为完数。例如61+2+3(6的因子是1,2,3)。 现在,你要写一个程序,读入两个正整数n和m(1<n<m<…...

国庆day6
国庆day6 汇编语言的组成 伪操作 不参与程序的执行,但是用于告诉编译器程序该怎么编译 如: .text .global .end .if .else .endif .data汇编指令 汇编器将一条汇编指令编译成一条机器码,在内存里一…...

力扣 -- 873. 最长的斐波那契子序列的长度
解题步骤: 参考代码: class Solution { public:int lenLongestFibSubseq(vector<int>& nums) {int nnums.size();unordered_map<int,int> hash;for(int i0;i<n;i){hash[nums[i]]i;}int ret2;vector<vector<int>> dp(n,v…...
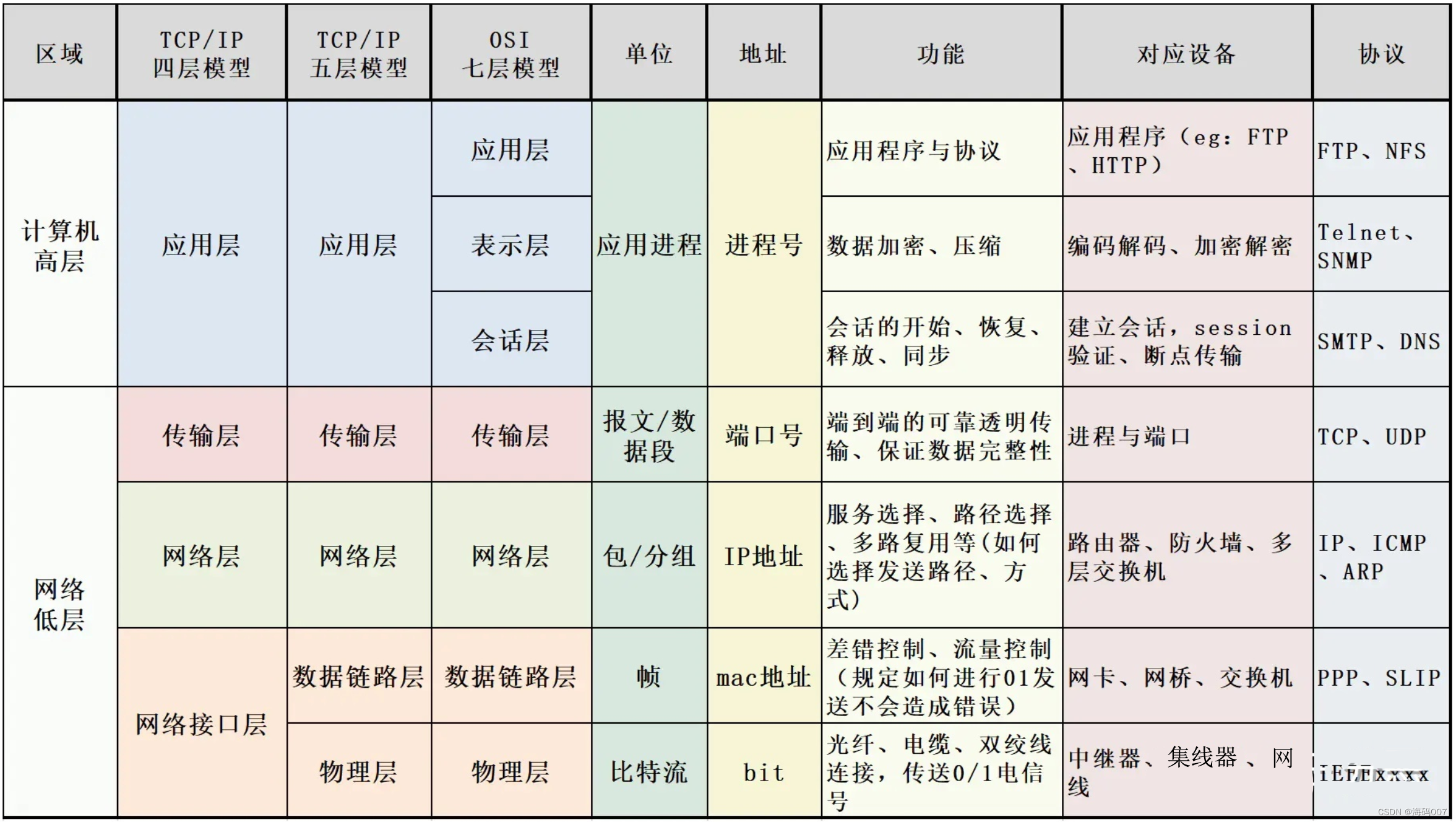
【程序员必看】计算机网络,快速了解网络层次、常用协议和物理设备!
文章目录 0 引言1 基础知识的定义1.1 计算机网络层次1.2 网络供应商 ISP1.3 猫、路由器、交换机1.4 IP协议1.5 TCP、UDP协议1.6 HTTP、HTTPS、FTP协议1.7 Web、Web浏览器、Web服务器1.8 以太网和WLAN1.9 Socket (网络套接字) 2 总结 0 引言 在学习的过程…...

1.软件测试基础
一、软件测试概念 1.什么是软件 软件是计算机程序,是由计算机代码编写的一系列指令和数据,可以实现各种功能。它指的是计算机系统中的应用程序,包括操作系统、应用软件、驱动程序等。软件可以通过编程语言编写和开发,并可以安装…...

综合布线系统概述
对于现代化的大楼,其内部信息传输通道系统(综合布线系统) 已不仅仅要求能支持一般的语音传输,还应能够支持多种计算机网络 协议及多种厂商设备的信息互连,可适应各种灵活的,容错的组网方 案,…...

Labview 实战 99乘法表
基于新手小白,使用Labview实现99乘法表,敢于发表自己的一点方法,还请各位大侠放过! 如下: 运行效果如下: 思路为:将要显示出来的数据,全部转换为字符串形式,再塞入到数组…...
需求变化频繁的情况下,如何实施自动化测试
一.通常来说,具备以下3个主要条件才能开展自动化测试工作: 1.需求变动不频繁 自动化测试脚本变化的频率决定了自动化测试的维护成本。如果需求变动过于频繁,那么测试人员就需要根据变动的需求来不断地更新自动化测试用例,从而适应新的功能。…...
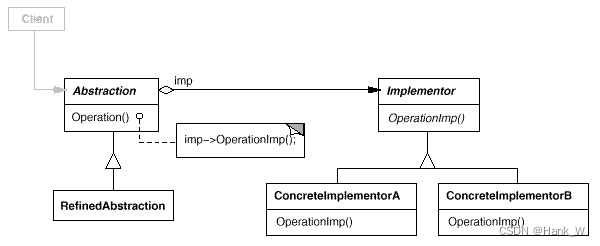
C++设计模式-桥接(Bridge)
目录 C设计模式-桥接(Bridge) 一、意图 二、适用性 三、结构 四、参与者 五、代码 C设计模式-桥接(Bridge) 一、意图 将抽象部分与它的实现部分分离,使它们都可以独立地变化。 二、适用性 你不希望在抽象和它…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
