李沐深度学习记录5:13.Dropout
Dropout从零开始实现
import torch
from torch import nn
from d2l import torch as d2l# 定义Dropout函数
def dropout_layer(X, dropout):assert 0 <= dropout <= 1# 在本情况中,所有元素都被丢弃if dropout == 1:return torch.zeros_like(X)# 在本情况中,所有元素都被保留if dropout == 0:return X#torch.rand生成0-1之间的均匀分布随机数,将其值与dropout概率作比较,得到布尔类型结果由mask存储#布尔类型为0的则为随机丢弃置0的隐藏层单元,留下的则进行值的替换h-->h/(1-p)mask = (torch.rand(X.shape) > dropout).float()return mask * X / (1.0 - dropout)# 测试dropout函数
# X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
# print(X)
# print(dropout_layer(X, 0.))
# print(dropout_layer(X, 0.5))
# print(dropout_layer(X, 1.))#定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256#定义模型
dropout1, dropout2 = 0.2, 0.5class Net(nn.Module): #写一个模型类继承nn.Moduledef __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,is_training = True):super(Net, self).__init__()self.num_inputs = num_inputsself.training = is_training#定义三个全连接层和激活函数self.lin1 = nn.Linear(num_inputs, num_hiddens1)self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)self.lin3 = nn.Linear(num_hiddens2, num_outputs)self.relu = nn.ReLU()def forward(self, X):H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs)))) #第一层全连接层加激活函数# 只有在训练模型时才使用dropoutif self.training == True:# 在第一个全连接层之后添加一个dropout层H1 = dropout_layer(H1, dropout1)H2 = self.relu(self.lin2(H1))if self.training == True:# 在第二个全连接层之后添加一个dropout层H2 = dropout_layer(H2, dropout2)out = self.lin3(H2)return outnet = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)#训练和测试
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)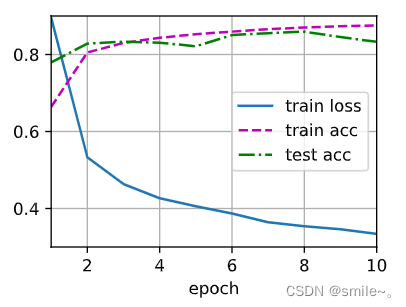
Dropout简洁实现
import torch
from torch import nn
from d2l import torch as d2l#定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256#定义模型
dropout1, dropout2 = 0.2, 0.5#定义模型
net=nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),#第一个全连接层之后添加一个Dropout层nn.Dropout(dropout1),nn.Linear(256,256),nn.ReLU(),#第二个全连接层之后添加一个Dropout层nn.Dropout(dropout2),nn.Linear(256,10))
#参数初始化
def init_weights(m):if type(m)==nn.Linear:nn.init.normal_(m.weight,std=0.01)net.apply(init_weights)

#读取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)#训练测试
num_epochs,lr=10,0.5
loss = nn.CrossEntropyLoss(reduction='none')
trainer=torch.optim.SGD(net.parameters(),lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
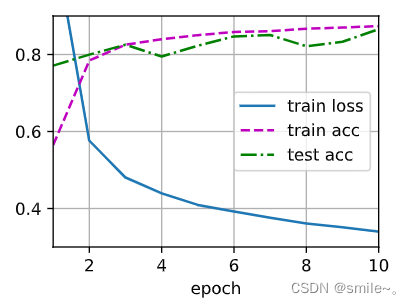
相关文章:

李沐深度学习记录5:13.Dropout
Dropout从零开始实现 import torch from torch import nn from d2l import torch as d2l# 定义Dropout函数 def dropout_layer(X, dropout):assert 0 < dropout < 1# 在本情况中,所有元素都被丢弃if dropout 1:return torch.zeros_like(X)# 在本情况中&…...

计算机竞赛 题目:基于大数据的用户画像分析系统 数据分析 开题
文章目录 1 前言2 用户画像分析概述2.1 用户画像构建的相关技术2.2 标签体系2.3 标签优先级 3 实站 - 百货商场用户画像描述与价值分析3.1 数据格式3.2 数据预处理3.3 会员年龄构成3.4 订单占比 消费画像3.5 季度偏好画像3.6 会员用户画像与特征3.6.1 构建会员用户业务特征标签…...
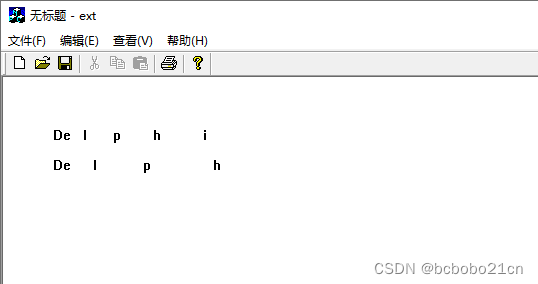
MFC ExtTextOut函数学习
ExtTextOut - 扩展的文本输出; win32 api的声明如下; ExtTextOut( DC: HDC; {设备环境句柄} X, Y: Integer; {起点坐标} Options: Longint; {选项} Rect: PRect; {指定显示范围; 0 表示限制范围} Str: PChar; {字符串…...

Java中阻塞队列原理、特点、适用场景
文章目录 阻塞队列对比、总览阻塞队列本质思想主要队列讲解ArrayBlockingQueueLinkedBlockingQueueSynchronousQueueLinkedTransferQueuePriorityBlockingQueueDelayQueueLinkedBlockingDeque 阻塞队列对比、总览 阻塞队列本质思想 阻塞队列都是线程安全的队列. 其最主要的功能…...

PHP之linux、apache和nginx与安全优化面试题
1.linux常用命令 查看目录pwd 创建文件touch 创建目录mkdir 删除文件rm 删除目录rmdir移动改名文件 mc 查询目录find 修改权限chmod 压缩包 tar 安装 yum install 修改文件vi查看进程ps 停止进程kill 定时任务crontab 2、nginx的优化 gzip压缩优化 expires缓存…...

算法笔记:0-1背包问题
n个商品组成集合O,每个商品有两个属性vi(体积)和pi(价格),背包容量为C。 求解一个商品子集S,令 优化目标 1. 枚举所有商品组合 共2^n - 1种情况 2. 递归求解 KnapsackSR(h, i, c)ÿ…...
C++入门-day02
引言:在上一节中我们接触了C中的命名空间,学会了C中的标准输出流。这一节,我标题一们讲讲缺省、重载。 一、缺省参数 在C中,给函数的形参默认给一个值就是缺省参数,你可能会比较懵逼,下面看一段代码。 正常…...
)
模板方法模式,基于继承实现的简单的设计模式(设计模式与开发实践 P11)
文章目录 实现举例应用钩子 Hook 模板方法模式是一种基于继承的设计模式,由两部分构成: 抽象父类(一般封装了子类的算法框架)具体的实现子类 实现 简单地通过继承就可以实现 举例 足球赛 和 篮球赛 都有 3 个步骤,…...
php://input输入流)
php实战案例记录(16)php://input输入流
php://input是PHP中的一个特殊的输入流,它允许访问请求的原始数据。它主要用于处理非表单的POST请求,例如当请求的内容类型为application/json或application/xml时。使用php://input可以获取到POST请求中的原始数据,无论数据是什么格式。使用…...

cad图纸如何防止盗图(一个的制造设计型企业如何保护设计图纸文件)
在现代企业中,设计图纸是公司的重要知识产权,关系到公司的核心竞争力。然而,随着技术的发展,员工获取和传播设计图纸的途径越来越多样化,如何有效地防止员工复制设计图纸成为了企业管理的一大挑战。本文将从技术、管理…...
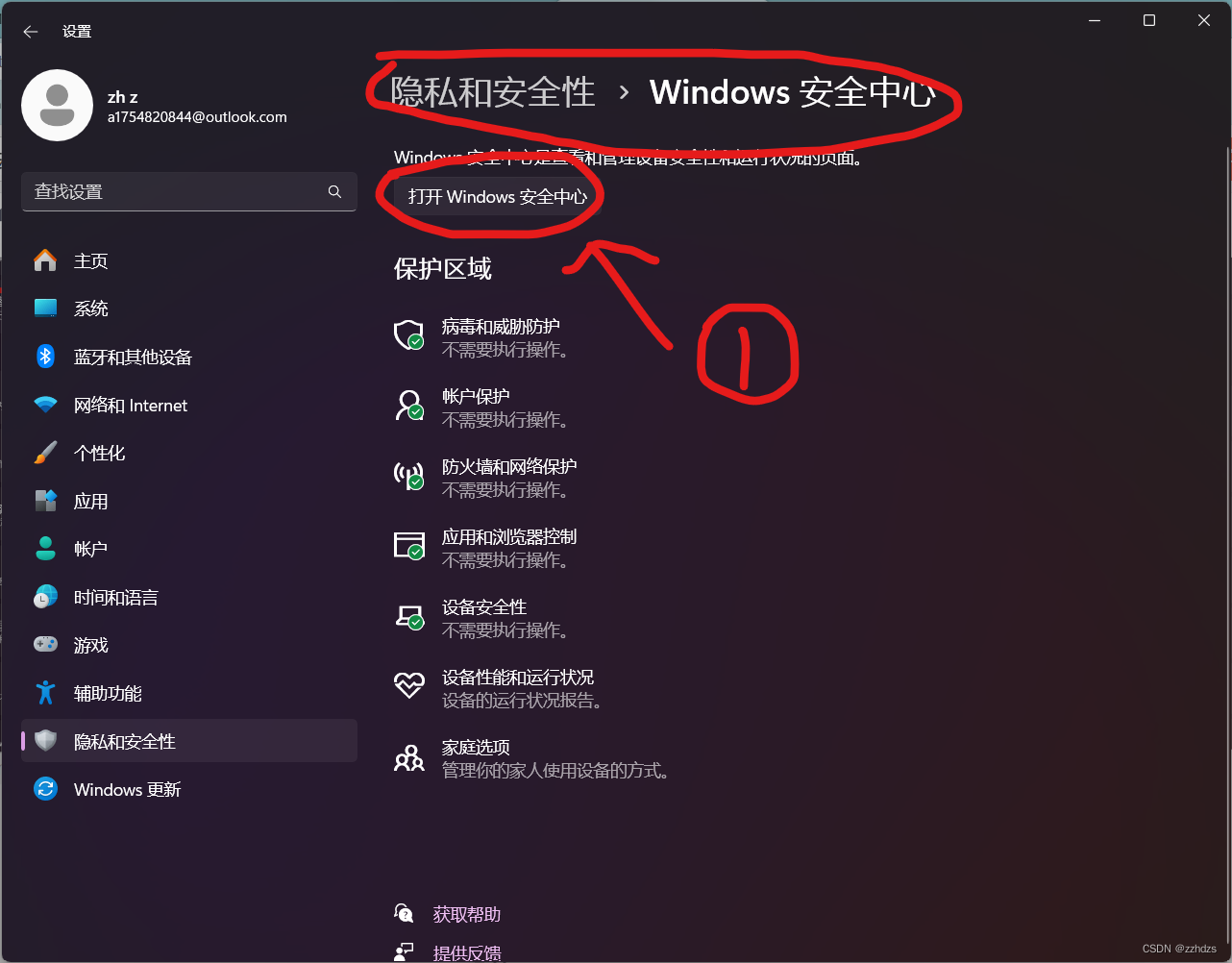
Windows11 安全中心页面不可用问题(无法打开病毒和威胁防护)解决方案汇总(图文介绍版)
本文目录 Windows版本与报错信息问题详细图片: 解决方案:方案一、管理员权限(若你确定你的电脑只有你一个账户,则此教程无效,若你也不清楚,请阅读后再做打算)方案二、修改注册表(常用方案)方案三、进入开发…...

1329: 【C2】【排序】奖学金
题目描述 某小学最近得到了一笔赞助,打算拿出其中一部分为学习成绩优秀的前5名学生发奖学金。期末,每个学生都有3门课的成绩:语文、数学、英语。先按总分从高到低排序,如果两个同学总分相同,再按语文成绩从高到低排序,…...
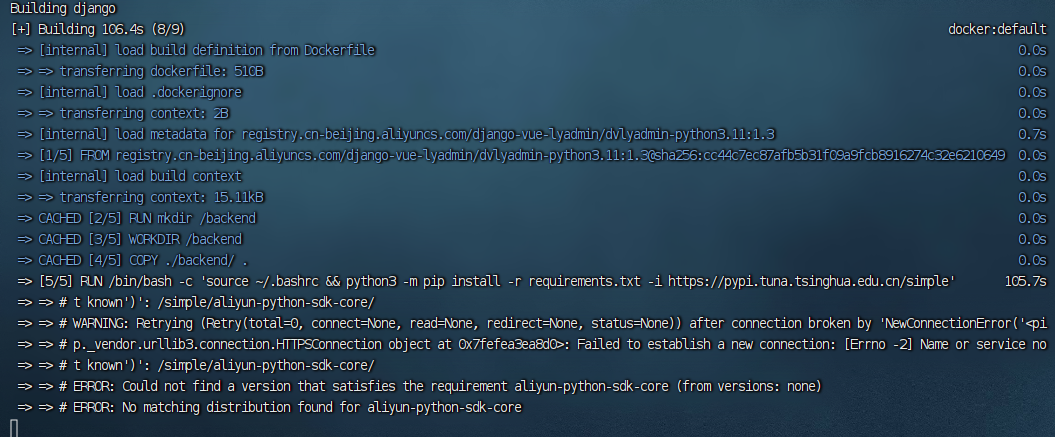
解决dockerfile创建镜像时pip install报错的bug
项目场景: 使用docker-compose创建django容器 问题描述 > [5/5] RUN /bin/bash -c source ~/.bashrc && python3 -m pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple: 0.954 Looking in indexes: https://…...
算法题:分发饼干
这个题目是贪心算法的基础练习题,解决思路是排序双指针谈心法,先将两个数组分别排序,优先满足最小胃口的孩子。(本题完整题目附在了最后面) 代码如下: class Solution(object):def findContentChildren(se…...

WebSocket编程golang
WebSocket编程 WebSocket协议解读 websocket和http协议的关联: 都是应用层协议,都基于tcp传输协议。跟http有良好的兼容性,ws和http的默认端口都是80,wss和https的默认端口都是443。websocket在握手阶段采用http发送数据。 we…...

PHP之redis 和 memache面试题
目录 1、什么是Redis?它的主要特点是什么? 2、redis数据类型 3、Redis的持久化机制有哪些?它们之间有什么区别? 4、Redis的主从复制是什么?如何配置Redis的主从复制? 5、Redis的集群模式是什么…...
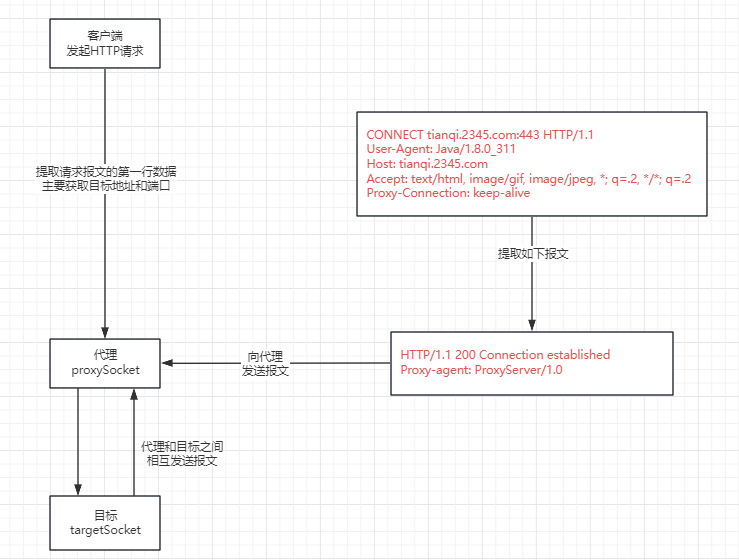
java socket实现代理Android App
实现逻辑就是转发请求和响应。 核心代码 // 启动代理服务器private void startProxyServer() {new Thread(new ProxyServer()).start();}// 代理服务器static class ProxyServer implements Runnable {Overridepublic void run() {try {// 监听指定的端口int port 8098; //一…...
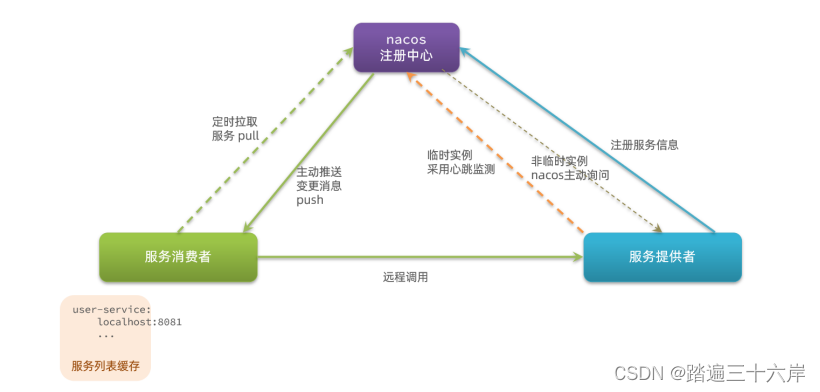
Nacos与Eureka的区别
大家好我是苏麟今天说一说Nacos与Eureka的区别. Nacos Nacos的服务实例分为两种l类型: 临时实例:如果实例宕机超过一定时间,会从服务列表剔除,默认的类型。非临时实例:如果实例宕机,不会从服务列表剔除&…...

浅谈Rob Pike的五条编程规范
又是一篇需要我们多些思考的文章~ 简介下Rob Pike Rob Pike是Unix的先驱,UTF-8的设计人,Go语言核心设计者之一。 Rob Pike的5条编程规则 原文地址:http://users.ece.utexas.edu/~adnan/pike.html 中文翻译: 罗布派克&#x…...

LeetCode 377.组合总和IV 可解决一步爬m个台阶到n阶楼顶问题( 完全背包 + 排列数)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围 示例 1: 输入:nums [1,2,3], target 4 输出:7 解释&#x…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
