LeetCode 377.组合总和IV 可解决一步爬m个台阶到n阶楼顶问题( 完全背包 + 排列数)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3 输出:0
>>思路和分析
本题中顺序不同的序列被视为不同的组合,其实就是求排列!
(1)区分组合和排列:
组合:不强调顺序,(1,5) 和 (5,1)是同一个组合
排列:是强调顺序,(1,5) 和 (5,1)是两个不同的排列
可知本题的本质求的是排列总和,且仅仅求的是排列总和的个数,并不是把所有的排列都列出来~
若本题需要把排列都列出来的话,只能用回溯算法暴搜!
>>动规五部曲分析如下:
1.确定dp数组以及下标的含义
dp[j] : 凑成目标正整数为 j 的排列个数为 dp[j]
2.确定递归公式
dp[j] (考虑nums[i])可以由dp[j - nums[i]] (不考虑nums[i]) 推导出来
因为只要得到 nums[i],排列个数 dp[j - nums[i]],就是dp[i]的一部分
在动态规划:494.目标和 和 动态规划:518.零钱兑换II 中我们已经讲过了,求装满背包有几种方法,递推公式一般都是 dp[j] += dp[j-nums[i]]; 本题一样!
3.dp数组初始化
因为 dp[j] += dp[j - nums[i]] ,所以dp[0]要初始化为1,这样递归其他dp[j]的时候才会有数值基础
dp[0] = 1;其实是没有意义的,因为题目中说了,给定的目标值是正整数,所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
非0下标的dp[j] 应该初始为0,这样才不会影响dp[j] 累加所有的 dp[j - nums[i]];
4.确定遍历顺序
个数是可以不限制使用的,所以本题可以使用完全背包来解决,得到的集合是排列,说明需要考虑元素之间的顺序。因为本题要求的是排列,那么需要格外注意for循环嵌套的顺序~
在动态规划:518 零钱兑换II 中讲到:
- 如果求组合数就是外层 for 循环遍历物品,内层for循环遍历背包
- 如果求排列数就是外层 for 循环遍历背包,内层for循环遍历物品
举个例子:计算dp[4]时,结果集想要有{1,3},{3,1}这两个集合,那么得先遍历背包,再遍历物品,才可以;反之则结果集只有{1,3}这样的集合。
因此可以确定本题遍历顺序最终的遍历顺序为:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前向后遍历(完全背包)
5.举例来推导dp数组

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target+1,0);dp[0] = 1;// 排列数for(int j = 0;j <= target;j++) { // 背包for(int i=0;i < nums.size();i++) { // 物品if(j >= nums[i] && dp[j] < INT_MAX - dp[j - nums[i]])dp[j] += dp[j-nums[i]];}}return dp[target];}
};// [0-i] 装满背包为j 有dp[j]种
// dp[j] += dp[j-nums[i]]- 时间复杂度:O(target * n),其中 n 为nums的长度
- 空间复杂度:O(target)
C++测试用例有两个数相加超过int的数据,所以需要在 if 里加上dp[j] < INT_MAX - dp[j - nums[i]]
参考和推荐文章、视频:
代码随想录 (programmercarl.com)
动态规划之完全背包,装满背包有几种方法?求排列数?| LeetCode:377.组合总和IV_哔哩哔哩_bilibili
往期文章:
完全背包 动态规划 + 一维dp数组
LeetCode 518.零钱兑换II 动态规划 + 完全背包 + 组合数
【总结】
- 求装满背包有几种方法,递归公示都是一样的,没有差别,但关键在于遍历顺序!
- 本题与动态规划:518.零钱兑换II 的区别,一个是求排列数,一个是求组合数,遍历顺序完全不同。
来自代码随想录的课堂截图!

爬楼梯拓展成一步可以爬m个台阶,这个代码怎么写?思路是怎么样的?
leetCode 70.爬楼梯 动态规划_呵呵哒( ̄▽ ̄)"的博客-CSDN博客
好问题:若一步一个台阶,两个台阶,三个台阶,直到 m 个台阶,有多少种方法爬到n阶楼顶。一步可以爬几个台阶,其实就是相当于每个物品,有多少种不同的方法可以爬到楼顶,相当于装满这个背包有多少种方法。比如:如果说我们先爬了一步再爬两步,再爬一步可到楼顶。和我们先爬一步,再爬一步,后爬了两步到了楼顶。请问这是几种爬楼梯的方法?很明显,这是两种方法,所以说爬楼梯的话,我们求的这个集合的个数,我们要强调元素的顺序,所以说和本题(leetCode 377.组合总和IV)是一样的。同样是强调元素之间的顺序的,也就是说 {1,2,1} 和 {1,1,2} 这是两个集合,要分别来计数。
class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1,0);dp[0] = 1;int m = 2;// m 表示一步最多可以爬多少个台阶for(int j = 1;j <= n; j++) { // 背包for(int i = 1;i <= m; i++) { // 物品if(j >= i)dp[j] += dp[j-i];}}return dp[n];}
};代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题70.爬楼梯可以AC的代码了。
相关文章:

LeetCode 377.组合总和IV 可解决一步爬m个台阶到n阶楼顶问题( 完全背包 + 排列数)
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围 示例 1: 输入:nums [1,2,3], target 4 输出:7 解释&#x…...
C中volatile总结
在CPU处理过程中,需要将内存中的数据载入到寄存器中才能计算,所以可能涉及到一个问题,如果内存中的数据被更改了,但是寄存器还是使用的旧数据,这样就会造成数据的不同步。 一、volatile关键字的作用 使用volatile关键…...
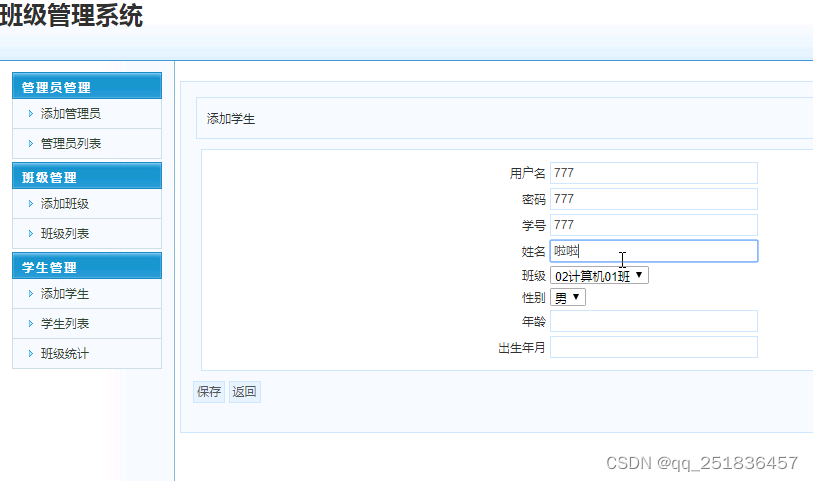
asp.net班级管理系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net班级管理系统 是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语言开发 asp.net班级管理系统 二、功能介绍 1…...
【Pytorch笔记】6.Transforms
pytorch官方文档 - transforms transforms需要使用计算机视觉工具包:torchvision。 torchvision.transforms:常用的图像预处理方法; torchvision.datasets:常用数据集的dataset实现,如MNIST、CIFAR-10、ImageNet等&am…...

nodejs+vue临沂特色产品销售平台elementui
从实际工作出发,对过去的临沂特色产品销售平台存在的问题进行分析,完善用户的使用体会。采用计算机系统来管理信息 提高了工作的效率。 随着信息化社会的形成和微电子技术日新月异的发展,临沂特色产品销售平台是针对目前临沂特色产品销售…...

机器学习必修课 - 使用管道 Pipeline
目标:学习使用管道(pipeline)来提高机器学习代码的效率。 1. 运行环境:Google Colab import pandas as pd from sklearn.model_selection import train_test_split!git clone https://github.com/JeffereyWu/Housing-prices-dat…...

WEB各类常用测试工具
一、单元测试/测试运行器 1、Jest 知名的 Java 单元测试工具,由 Facebook 开源,开箱即用。它在最基础层面被设计用于快速、简单地编写地道的 Java 测试,能自动模拟 require() 返回的 CommonJS 模块,并提供了包括内置的测试环境 …...

Naive UI 文档地址
最近几天官网访问不了,自己用github pages 部署了个 官网 github pages...

在CentOS7系统中安装MySQL5.7
第一步:下载MySQL包 > wget http://repo.mysql.com/mysql57-community-release-el7-10.noarch.rpm第二步:安装MySQL源 > rpm -Uvh mysql57-community-release-el7-10.noarch.rpm第三步:安装MySQL服务端 > yum install -y mysql-c…...
R语言通过接口获取网上数据平台的免费数据
大家好,我是带我去滑雪! 作为一名统计学专业的学生,时常和数据打交道,我深知数据的重要性。数据是实证研究的重要基础,每当在完成一篇科研论文中的实证研究部分时,我都能深刻体会实证研究最复杂、最耗时的工…...
【Docker内容大集合】Docker从认识到实践再到底层原理大汇总
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总https://blog.csdn.net/yu_cblog/categ…...
算法题:摆动序列
这道题是一道贪心算法题,如果前两个数是递增,则后面要递减,如果不符合则往后遍历,直到找到符合的。(完整题目附在了最后) 代码如下: class Solution(object):def wiggleMaxLength(self, nums):…...
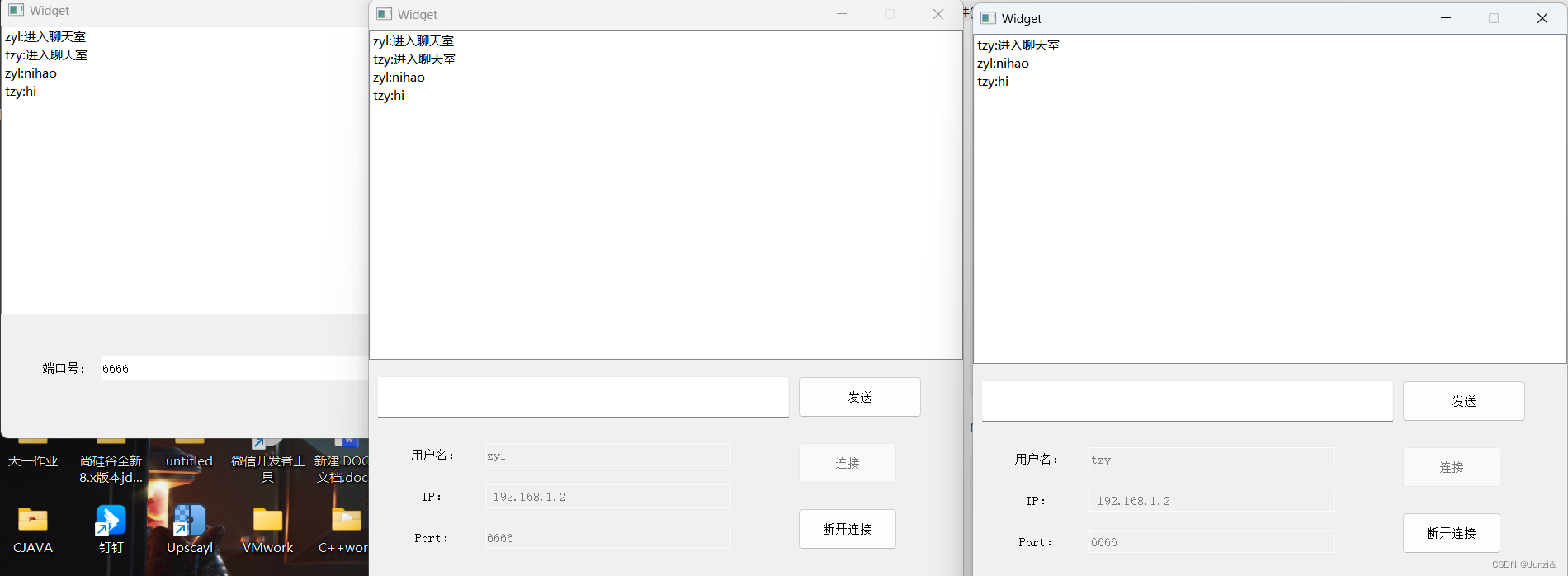
复习 --- QT服务器客户端
服务器: 头文件: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include<QTcpServer> #include<QTcpSocket> #include<QMessageBox> #include<QDebug> #include<QList> #include<QListWidget> #in…...

Godot 官方2D游戏笔记(1):导入动画资源和添加节点
前言 Godot 官方给了我们2D游戏和3D游戏的案例,不过如果是独立开发者只用考虑2D游戏就可以了,因为2D游戏纯粹,我们只需要关注游戏的玩法即可。2D游戏的美术素材简单,交互逻辑简单,我们可以把更多的时间放在游戏的玩法…...

leetcode 热题 100
数组和字符串匹配 子串和子序列 原串:“abcabc” 子串:“abc”, 连续但不大于原串的字符串 子序列:“acc”, 字符来自原串且保持在原串中顺序不变的字符串 子排列: “aabbcc”, 字符来自原串且只能用1次,但可有不同排列顺序的字…...

Ae 效果:CC Lens
扭曲/CC Lens Distort/CC Lens CC Lens (CC 镜头)主要用于添加或移除摄像机镜头扭曲,比如桶形失真 Barrel、枕形失真 Pincushion以及鱼眼失真 Fisheye等。或者,用它来创建一些特殊的动画效果。 ◆ ◆ ◆ 效果属性说明 Center 中…...
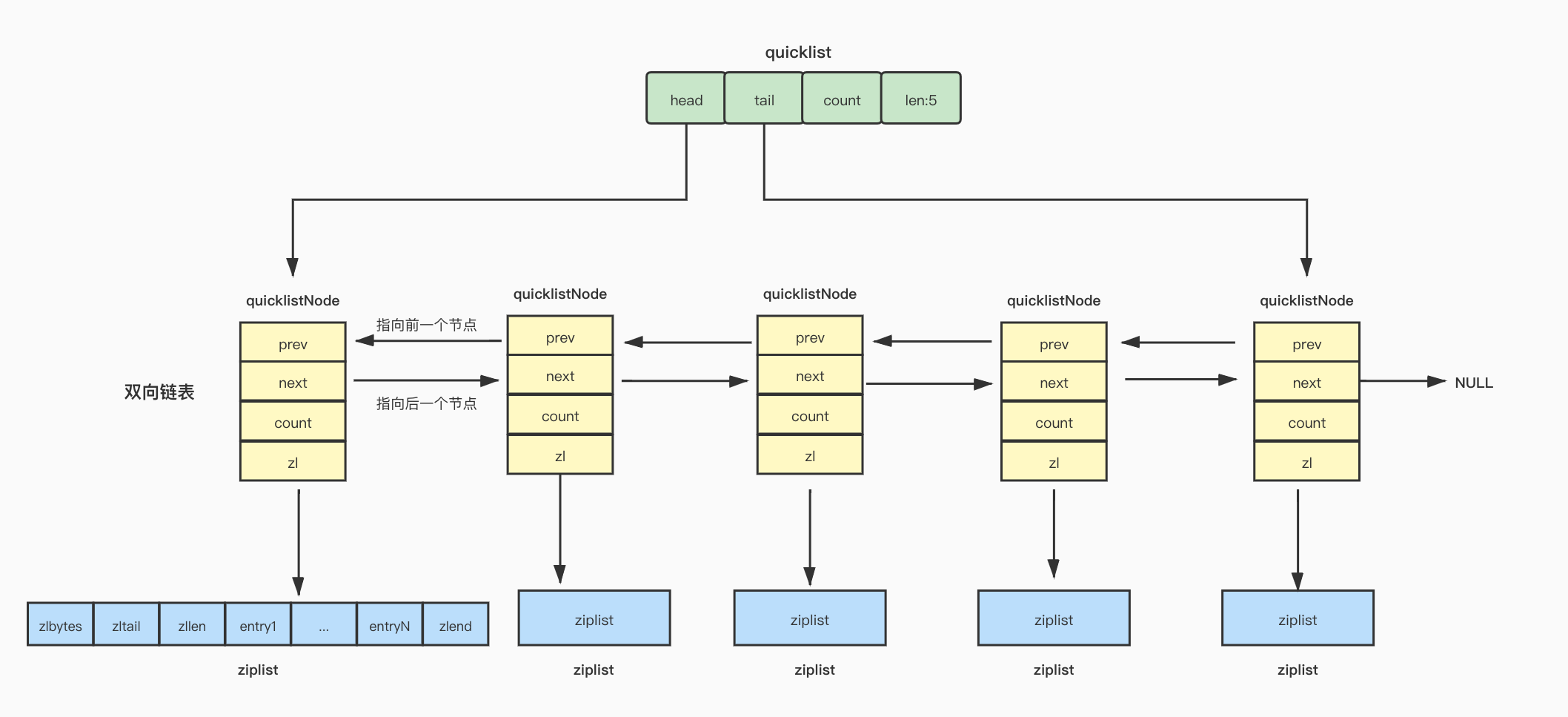
【Redis】基础数据结构-quicklist
Redis List 在Redis3.2版之前,Redis使用压缩列表和双向链表作为List的底层实现。当元素个数比较少并且元素长度比较小时,Redis使用压缩列表实现,否则Redis使用双向链表实现。 ziplist存在问题 不能保存过多的元素,否则查找复杂度…...

QT 实现服务器客户端搭建
1. 服务器头文件 #ifndef SER_H #define SER_H#include <QWidget> #include<QTcpServer> //服务器头文件 #include<QTcpSocket> //客户端头文件 #include<QMessageBox> //消息对话框 #include<QList> //链表头文件QT_BEGIN_NAM…...
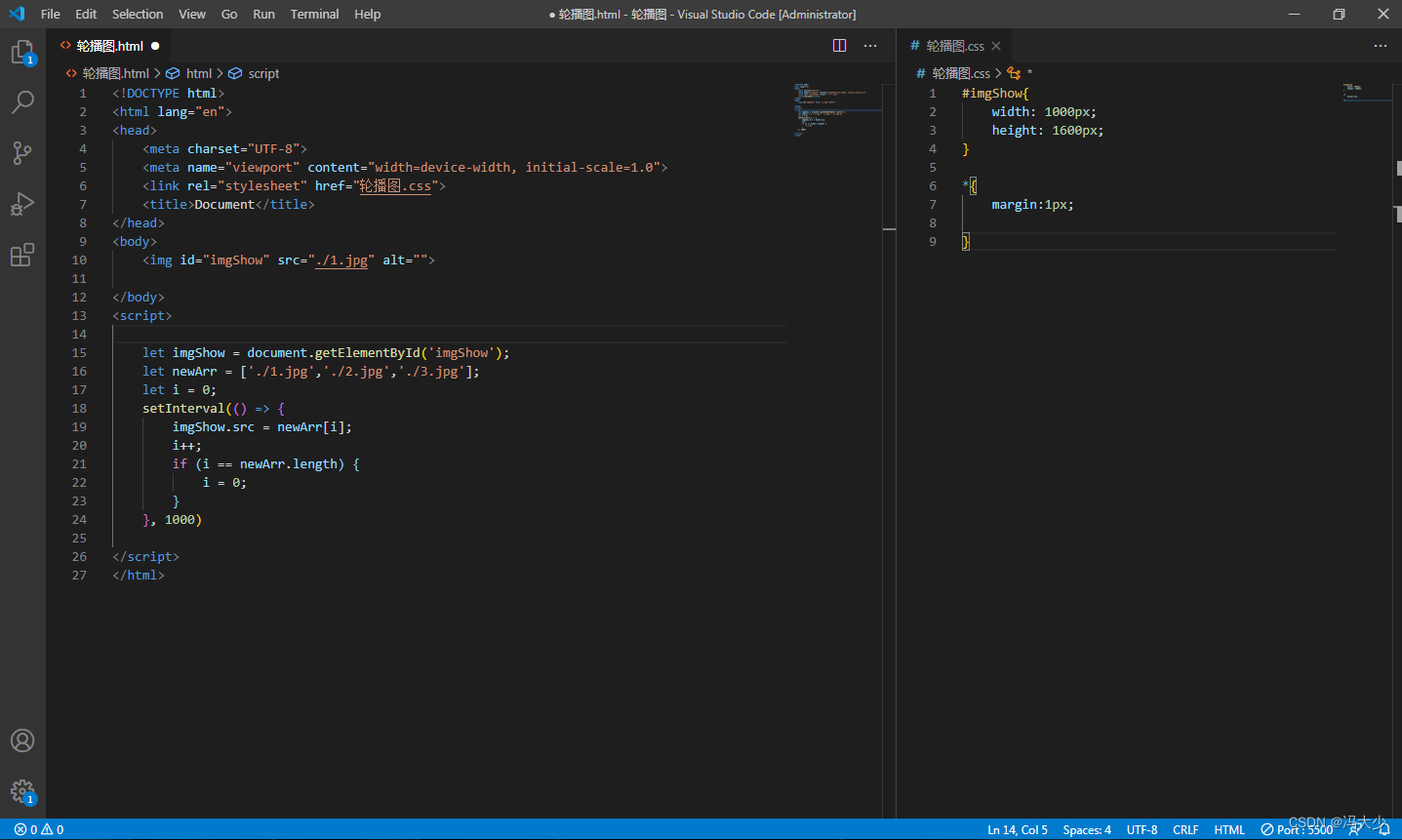
Javascript - 轮播图
轮播图也称banner图、广告图、焦点图、滑片。是指在一个模块或者窗口,通过鼠标点击或手指滑动后,可以看到多张图片。这些图片统称为轮播图,这个模块叫做轮播模块。可以通过运用 javascript去实现定时自动转换图片。以下通过一个小Demo演示如何运用Javascript实现。 <!DOCTYP…...

MATLAB中syms函数使用
目录 语法 说明 示例 创建符号标量变量 创建符号标量变量的向量 创建符号标量变量矩阵 管理符号标量变量的假设 创建和评估符号函数 syms函数的作用是创建符号标量和函数,以及矩阵变量和函数。 语法 syms var1 ... varN syms var1 ... varN [n1 ... nM] …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...
