Python Random模块详解
Random模块详解
随机数
random模块
- randint(a, b) 返回[a, b]之间的整数
- randrange ([start,] stop [,step]) 从指定范围内,按指定基数递增的集合中获取一个随机数,基数 缺省值为1。random.randrange(1,7,2)
- choice(seq) 从非空序列的元素中随机挑选一个元素,比如random.choice(range(10)),从0到9中 随机挑选一个整数。random.choice([1,3,5,7])
- 3.6开始提供choices,一次从样本中随机选择几个,可重复选择,可以指定权重
- random.shuffle(list) ->None 就地打乱列表元素
- sample(population, k) 从样本空间或总体(序列或者集合类型)中随机取出k个不同的元素,返回 一个新的列表
- random.sample([‘a’, ‘b’, ‘c’, ‘d’], 2)
- random.sample([‘a’, ‘a’], 2) 会返回什么结果
- 每次从样本空间采样,在这一次中不可以重复抽取同一个元素
import random
# 导入random模块
x = list(range(5))
# 定义一个变量x,x的值是一个列表,列表中有一个range(5)对象
x
# 输出结果 [0, 1, 2, 3, 4] 顺序显示
random.shuffle(x)
# x调用random的shuffle方法,shuffle方法就是洗牌的意思打乱顺序。
x
# 返回了一个全新列表,并且是打乱顺序的[2, 1, 0, 3, 4]
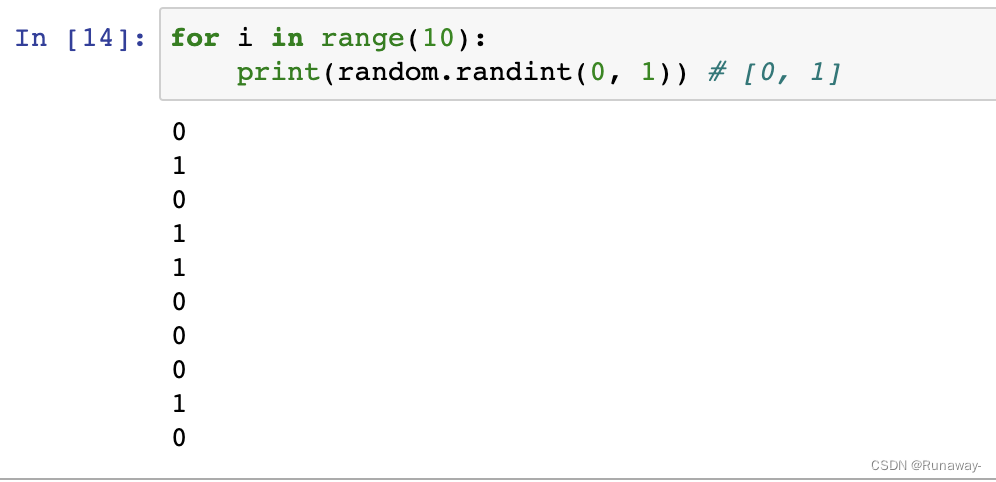
- 使用random的randint方法,获取0,1
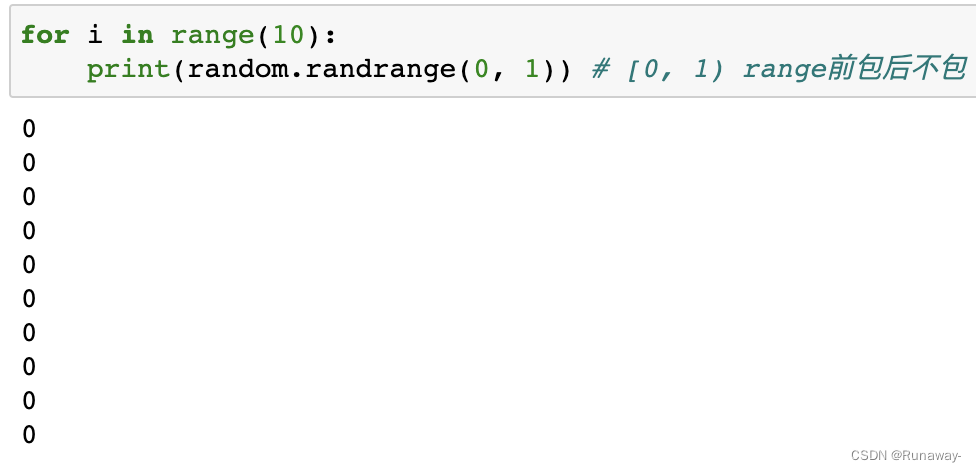
- 使用random的randrange方法,range对象,前包后不包。

- 随机取整,10永远也看不到,因为前包后不包。

print(random.choices(x))
# choices可以重复取


- [0, 1] 的范围内取6次,循环执行10次

- [0, 1] 的范围内取6次,[10, 1]权重1v1对应(出现10次0,出现1次1),循环执行10次

相关文章:

Python Random模块详解
Random模块详解 随机数 random模块 randint(a, b) 返回[a, b]之间的整数randrange ([start,] stop [,step]) 从指定范围内,按指定基数递增的集合中获取一个随机数,基数 缺省值为1。random.randrange(1,7,2)choice(seq) 从非空序列的元素中随机挑选一个…...

Vue3 模糊搜索筛选
Vue3 模糊搜索筛选 环境: vue3 tselement plus 目标: 输入框输入内容,对展示的列表进行模糊搜索筛选匹配的内容。 代码如下: <div style"margin-top: 50px"><el-input v-model"valueInput" size&…...
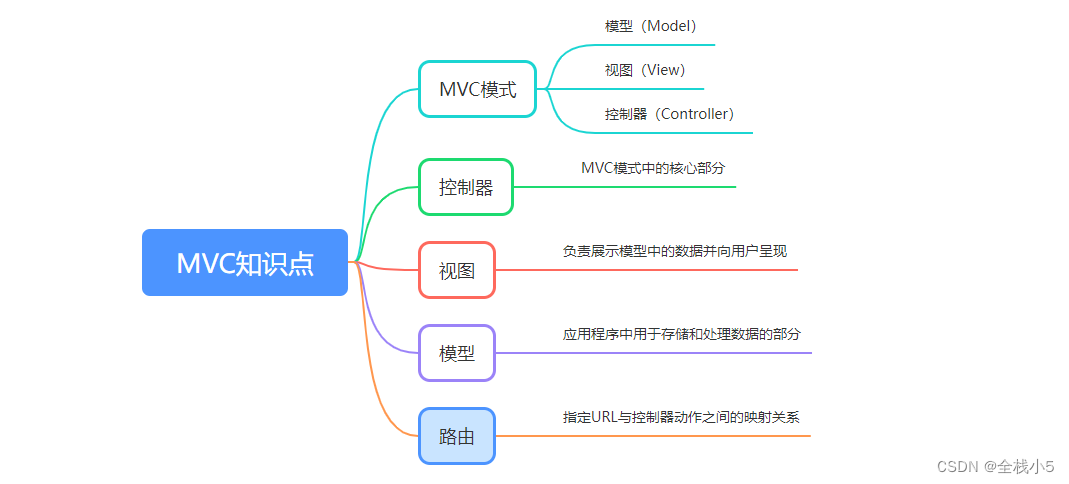
【MVC】C# MVC基础知识点、原理以及容器和管道
给自己一个目标,然后坚持一段时间,总会有收获和感悟! 国庆假期马上结束,闲暇时间,重温一遍C#关于MVC的技术,控制器、视图、模型,知识点和原理,小伙伴们还记得吗 目录 一、MVC知识点1…...
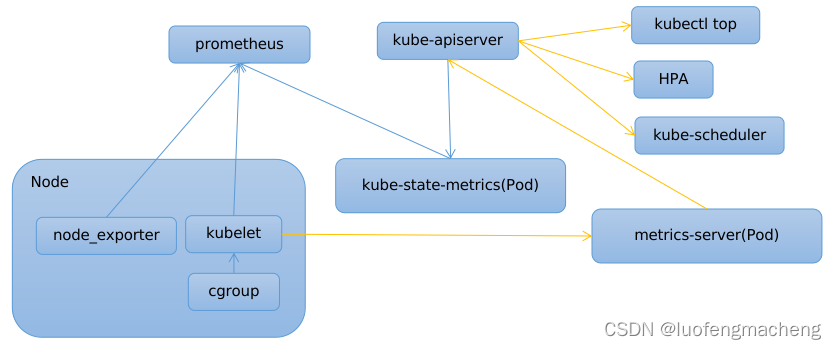
【kubernetes】基于prometheus的监控
目录 1 监控解决方案2 prometheus2.1 容器监控2.2 节点监控2.3 资源对象监控2.4 metrics--server 3 prometheus-operator vs kube-prometheus vs helm3.1 prometheus-operator3.2 kube-prometheus3.3 helm 参考文档 1 监控解决方案 从实现方案来说,监控分为3个部分…...

Gmail 将停止支持基本 HTML 视图
根据 Google 支持文档的更新内容,Gmail 将从明年 1 月起停止支持基本 HTML 视图。 ▲ Gmai 基本 HTML 视图界面 目前网页版 Gmail 提供两个界面:基本 HTML 视图和标准视图。停止支持基本 HTML 视图后,当前打开经典模式的基本 HTML 视图模式 …...

电影大师杂记
假期集中刷了好多书,游戏和电影,在虚拟世界里猛烈的各种闲逛,cyberpunk 2077到blade runner,到异形,到终结者,到星球大战&环太平洋,到工业光魔,还有各种编程的书。。。 hmmm&…...
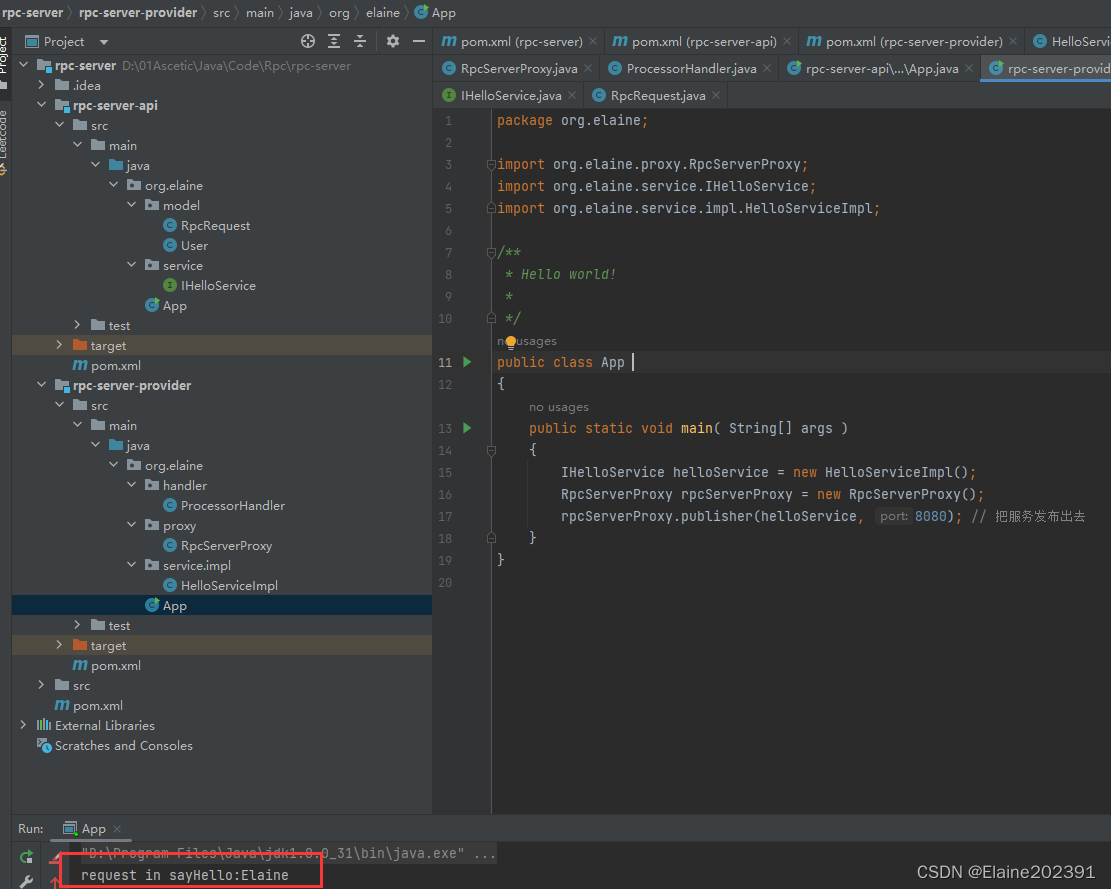
聊聊分布式架构——RPC通信原理
目录 RPC通信的基本原理 RPC结构 手撸简陋版RPC 知识点梳理 1.Socket套接字通信机制 2.通信过程的序列化与反序列化 3.动态代理 4.反射 思维流程梳理 码起来 服务端时序图 服务端—Api与Provider模块 客户端时序图 RPC通信的基本原理 RPC(Remote Proc…...

Android:实现手机前后摄像头预览同开
效果展示 一.概述 本博文讲解如何实现手机前后两颗摄像头同时预览并显示 我之前博文《OpenGLES:GLSurfaceView实现Android Camera预览》对单颗摄像头预览做过详细讲解,而前后双摄实现原理其实也并不复杂,粗糙点说就是把单摄像头预览流程写两…...
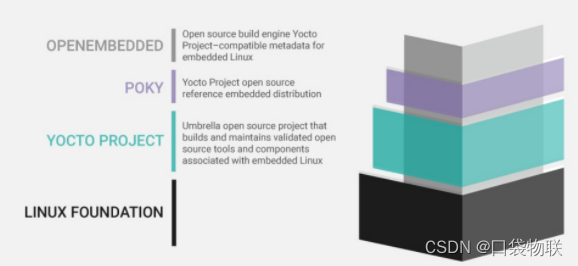
2.2.4 yocto poky openembedded bitbake关系
一 基本概念 The Yocto Project is an open-source project that delivers a set of tools that create operating system images for embedded Linux systems. Poky is the reference operating system distribution built with Yocto Project tools, and OpenEmbedded is a …...
)
开源后台管理系统 (go-vue-admin)
go-vue-admin 是一套基于go语言开源的后台管理系统。功能参考诺依网站 ,前后端分离。 简介 前端采用vue3、Element Plus 、RuoYi-Vue3后端采用gofrome 框架、mysql、redis、Jwt实现了一键生成前后端代码,高效开发。 内置功能 用户管理:用…...
想升级macOS Big Sur,但是MacBook内存空间不够该怎么办?
随着使用时间的增长,我们会发现Mac电脑的存储空间越来越少,这时候我们就需要对Mac电脑进行清理,以释放更多的存储空间。那么,Mac空间不足怎么解决呢? 1.清理垃圾文件 Mac空间不足怎么解决?首先要做的就是清…...

结构化面试 --- 介绍 + 人际关系
目录 一、介绍 1、认识考试 2、认识考官 3、认识对手 4、认识考场 5、认识规则 6、如何备考 二、人际关系 练习题 第一题(换岗) 第二题(办法) 第三题(相处) 第四题 第五题 第六题 …...
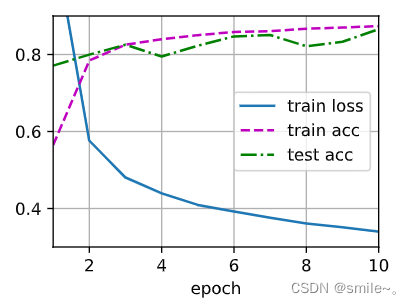
李沐深度学习记录5:13.Dropout
Dropout从零开始实现 import torch from torch import nn from d2l import torch as d2l# 定义Dropout函数 def dropout_layer(X, dropout):assert 0 < dropout < 1# 在本情况中,所有元素都被丢弃if dropout 1:return torch.zeros_like(X)# 在本情况中&…...

计算机竞赛 题目:基于大数据的用户画像分析系统 数据分析 开题
文章目录 1 前言2 用户画像分析概述2.1 用户画像构建的相关技术2.2 标签体系2.3 标签优先级 3 实站 - 百货商场用户画像描述与价值分析3.1 数据格式3.2 数据预处理3.3 会员年龄构成3.4 订单占比 消费画像3.5 季度偏好画像3.6 会员用户画像与特征3.6.1 构建会员用户业务特征标签…...
MFC ExtTextOut函数学习
ExtTextOut - 扩展的文本输出; win32 api的声明如下; ExtTextOut( DC: HDC; {设备环境句柄} X, Y: Integer; {起点坐标} Options: Longint; {选项} Rect: PRect; {指定显示范围; 0 表示限制范围} Str: PChar; {字符串…...

Java中阻塞队列原理、特点、适用场景
文章目录 阻塞队列对比、总览阻塞队列本质思想主要队列讲解ArrayBlockingQueueLinkedBlockingQueueSynchronousQueueLinkedTransferQueuePriorityBlockingQueueDelayQueueLinkedBlockingDeque 阻塞队列对比、总览 阻塞队列本质思想 阻塞队列都是线程安全的队列. 其最主要的功能…...

PHP之linux、apache和nginx与安全优化面试题
1.linux常用命令 查看目录pwd 创建文件touch 创建目录mkdir 删除文件rm 删除目录rmdir移动改名文件 mc 查询目录find 修改权限chmod 压缩包 tar 安装 yum install 修改文件vi查看进程ps 停止进程kill 定时任务crontab 2、nginx的优化 gzip压缩优化 expires缓存…...

算法笔记:0-1背包问题
n个商品组成集合O,每个商品有两个属性vi(体积)和pi(价格),背包容量为C。 求解一个商品子集S,令 优化目标 1. 枚举所有商品组合 共2^n - 1种情况 2. 递归求解 KnapsackSR(h, i, c)ÿ…...
C++入门-day02
引言:在上一节中我们接触了C中的命名空间,学会了C中的标准输出流。这一节,我标题一们讲讲缺省、重载。 一、缺省参数 在C中,给函数的形参默认给一个值就是缺省参数,你可能会比较懵逼,下面看一段代码。 正常…...
)
模板方法模式,基于继承实现的简单的设计模式(设计模式与开发实践 P11)
文章目录 实现举例应用钩子 Hook 模板方法模式是一种基于继承的设计模式,由两部分构成: 抽象父类(一般封装了子类的算法框架)具体的实现子类 实现 简单地通过继承就可以实现 举例 足球赛 和 篮球赛 都有 3 个步骤,…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
