Python学习-----无序序列2.0(集合的创建、添加、删除以及运算)
目录
前言:
什么是集合
集合的三大特性
1.集合的创建
(1)直接创建
(2)强制转换
2.集合的添加
(1)add()函数
(2)update() 函数
3.集合元素的删除
(1)remove() 函数
(2)discard() 函数
4.集合的运算
5.集合的应用----对列表去重
前言:
上一期讲了无序序列中的字典相关操作Python学习-----无序序列1.0(字典的创建、查看、添加、修改、删除/替换)_守约斯维奇的博客-CSDN博客 这一期来讲讲无序序列中的集合(set)的操作,包括创建、添加、删除已经集合之间的运算。
什么是集合
和数学中的集合概念一样,用来保存不重复的元素,即集合中的元素都是唯一的,互不相(高中都学过集合了,懂的都懂)
集合的三大特性
无序性
唯一性
互异性
1.集合的创建
(1)直接创建
格式:
集合名 = {元素,元素,元素……}
注意事项:集合是可变的(可以修改、添加、删除等等),但是里面的元素性质是不可变的,所以集合里面的元素不可以是列表类型、字典类型或者集合类型
示例1:(集合的无序性)
s={1,'qq',1.9,False}
print(s)
#输出结果:{'qq', 1, 1.9, False}集合本身是无序性的,所以输出结果也是没有按照顺序的,是随机顺序
示例2:(集合的互异性和唯一性)
s={1,1,2,2,2,1.6,False}
print(s)
#输出结果:{False, 1, 2, 1.6}这里面的1和2栋出现了重复,但是输出结果都是只保留了一个,这也是集合的互异性和唯一性
(2)强制转换
这里有一个问题,如果我想创建一个空集合怎么办,前面说了创建空字典直接 d = {},就行了,但是集合可不能用花括号,所以这里必须用强制转换set() 函数来实现
示例1:
#创建空字典 d={}#创建空集合
s = set()
print(s,type(s))
#输出结果:set() <class 'set'>示例2:
#强制转换把其他类型转换为集合
li=[1,2,5,3.5,False,(1,9.6)]
print(li,type(li))
#输出结果:[1, 2, 5, 3.5, False, (1, 9.6)] <class 'list'>
s=set(li)
print(s,type(s))
#输出结果:{False, 1, 2, 3.5, 5, (1, 9.6)} <class 'set'>2.集合的添加
(1)add()函数
格式:
集合名.add(元素)
添加方式:一次只能添加一个元素
集合本身是无序序列的,所以添加的元素的位置也是随机的放入一般都是用add() 函数去添加
示例1:
s = {1,2,3,3.14}
print(s)
s.add(False)
s.add('集合')
print(s)
示例2:
#通过循环来实现添加多个元素
s = {1,2,3,3.14}
q = {'瓦达西瓦','欧尼酱','空你几哇'}
for i in q:s.add(i)
print(s)
#输出结果:{1, 2, 3.14, 3, '空你几哇', '欧尼酱', '瓦达西瓦'}(2)update() 函数
格式:
集合.update([元素])
添加方式:这个函数可以添加单个元素,也可以一次性添加多个元素(添加多个元素比add() 函数简单,不需要用到循环)
注意事项:之前在字典的添加也用到了这个函数,但是添加字典是用花括号{}的,而添加集合里面是用中括号[ ] 的
s = {'李信','李华','李白'}
s.update(['瑶','澜'])
print(s)
#输出结果:{'瑶', '李白', '澜', '李信', '李华'}
3.集合元素的删除
(1)remove() 函数
格式:
集合名.remove(元素)
注意:一次性只可以移除一个元素,当元素不存在的时候将会报错
s = {'李信','李华','李白','瑶'}
s.remove('李华')
print(s)
#输出结果:{'瑶', '李信', '李白'}(2)discard() 函数
格式:
集合名.discard(元素)
注意: 当元素不存在的时候 不会报错(这也是与remove函数的区别)
s = {'李信','李华','李白','瑶'}
s.discard('瑶')
print(s)
#输出结果:{'李华', '李白', '李信'}4.集合的运算
| 符号 | 含义 |
|---|---|
| & | 交集,获得两个集合的公共元素 |
| | | 并集,获得两个集合的全部元素 |
| - | 差集,获得前面集合独有的元素 |
| ^ | 对称差集,获得两个几个除公共元素外的多有元素(并集-交集) |
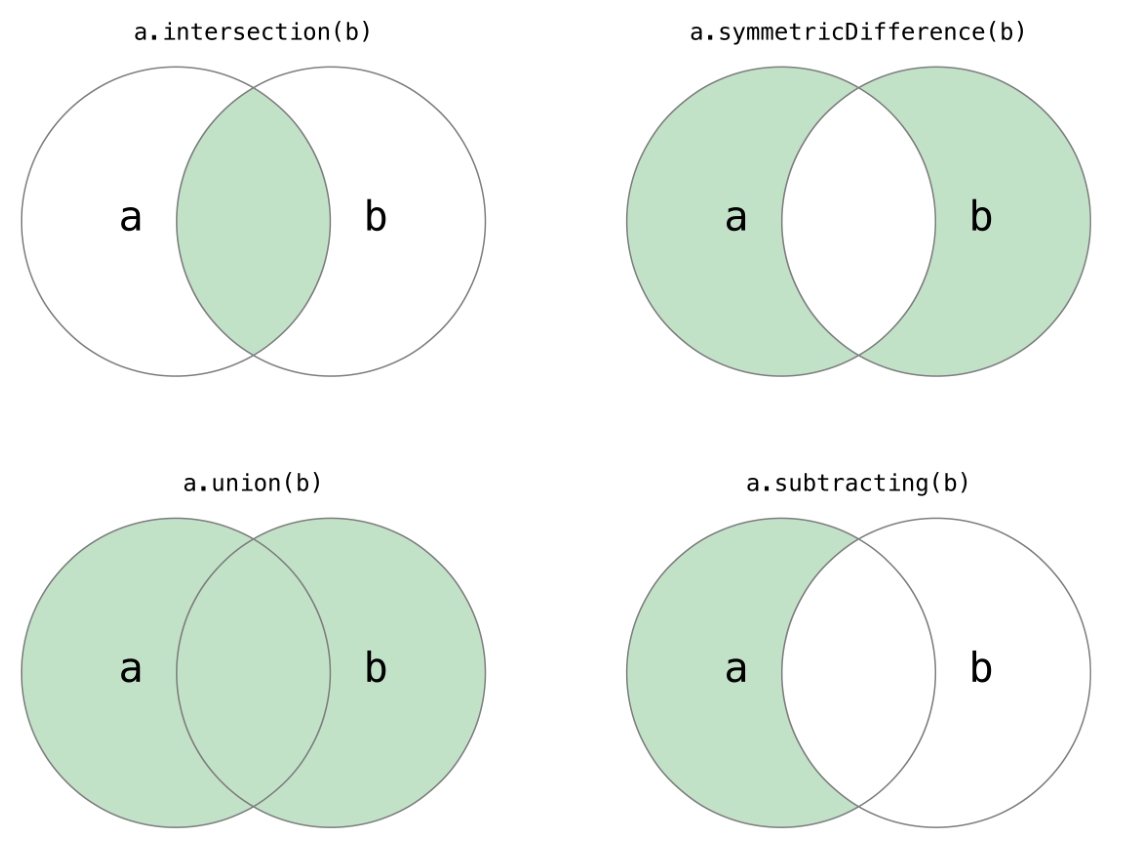
集合的运算跟高中我们学的基本上是一模一样的,交集、并集、补集。我不多解释了,看例题吧。
a = {1, 2, 4, 5, 6}
b = {1, 3, 5, 7}
print(a-b) #a对b的差集 a除去a与b重复的部分
print(b-a) #b对a的差集 b除去a与b重复的部分
print(b&a) #交集--a与b重复的部分
print(b|a) #并集--a与b的全部
print(a^b) # 等效于(a-b)|(b-a)
print((a-b)|(b-a)) 
集合运算很简单了,就不多讲了,多试试几个就行了
5.集合的应用----对列表去重
集合是有互异性的,唯一性的,如果出现重复的话,那么集合会舍弃重复的部分,只保留一个,所以我们可以通过集合的性质来实现去重,就以列表为例:
li=[1,1,5,5,'蔡徐坤',False]
print(li)
li=set(li)#转换为集合
print(li)
li=list(li)#转换回列表类型
print(li)
OK,这一期就到这里了,下课!!!
相关文章:

Python学习-----无序序列2.0(集合的创建、添加、删除以及运算)
目录 前言: 什么是集合 集合的三大特性 1.集合的创建 (1)直接创建 (2)强制转换 2.集合的添加 (1)add()函数 (2)update() 函数 3.集合元…...

2023最详细的接口测试用例设计教程
一、接口测试流程 1、需求讨论 2、需求评审 3、场景设计 4、数据准备 5、测试执行 二、分析接口文档元素 1、接口名称 2、接口地址 3、支持格式 4、请求方式 5、请求参数(参数名称、类型、是否必填、参数说明等) 6、返回参数(返回…...
【数据库】 数据库的理论基础详解
目录 一, 什么是数据库 二, 数据库管理系统(DBMS) 三,数据库与文件系统的区别 1,对比区别: 2,优缺点总结: 四,数据库的发展史 五,常见数据库 1, 关系型…...
Linux环境运行Maven 生成的hadoop jar包
运行命令: hadoop jar ./jar包名字 class对象路径 输入路径 输出路径 linux内部jar包测试 cd 到以下目录,创建以下文件夹 [rootreagan180 ~]# cd /opt/soft/hadoop313/share/hadoop/mapreduce/ 创建文件夹(读取路径) [roo…...
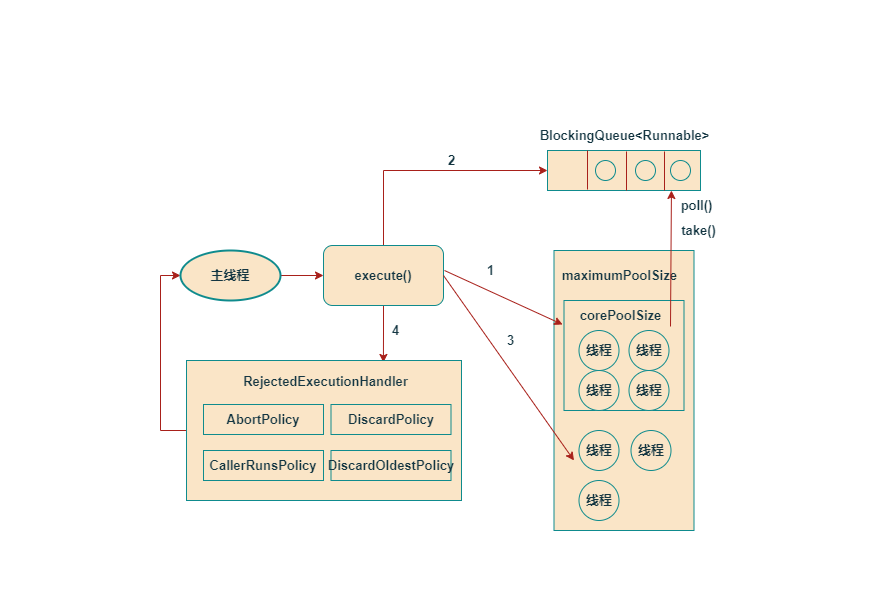
ThreadPoolExecutor原理解析
1. 工作原理1.1 流程图1.2 执行示意图从上图得知如果当前运行的线程数小于corePoolSize(核心线程数),则会创建新线程作为核心线程来执行任务(注意,执行这一步需要获取全局锁)。如果运行的线程等于或多于corePoolSize,则将任务加入BlockingQue…...

谷粒学苑第二章前端框架-2.2前端框架开发过程
一、前端框架开发过程 第一步:添加路由 src/router模块用来管理路由。 第二步:点击某个路由,显示路由对应页面内容 component: () > import(/views/table/index), 表示路由对应的页面,是views/table/index.vue页面 第三步&a…...
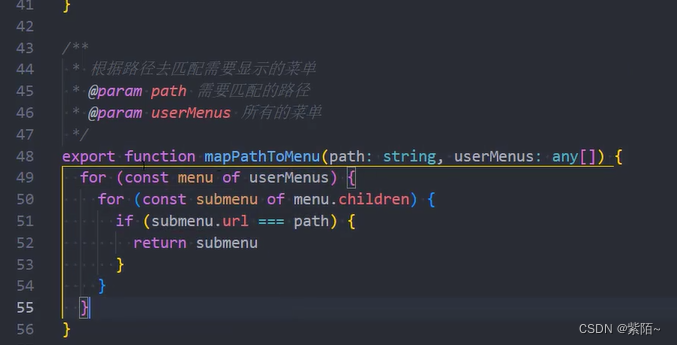
权限管理实现的两种方式(详解)
登录的接口请求的三个内容:1. token2. 用户信息、角色信息3. 菜单信息第一种:基于角色Role的动态路由管理 (不推荐,但市场用的比较多)首先列出枚举每个角色对应几个路由,然后根据用户登录的角色遍历枚举出来的角色动态注册对应的路…...

【C++】智能指针思路解析和模拟实现
此篇文章就从以下几个方面出发,带你了解智能指针的方方面面1.为什么需要智能指针当我们开辟内存并使用的时候,我们的顺序应该是这样:开辟内存-》使用内存-》释放内存问题就出现在第三步,开辟好了,也使用了,…...
:Sentinel流控降级入门)
SpringCloud(18):Sentinel流控降级入门
Sentinel本地应用流控降级实现分为三步: 创建本地应用搭建本地Sentinel控制台本地应用接入本地Sentinel控制台1 本地应用创建 整体流程分析 创建springboot项目在项目的pom.xml文件中引入sentinel-core的依赖坐标创建TestController,定义使用限流规则运行测试具体流程 1.创…...
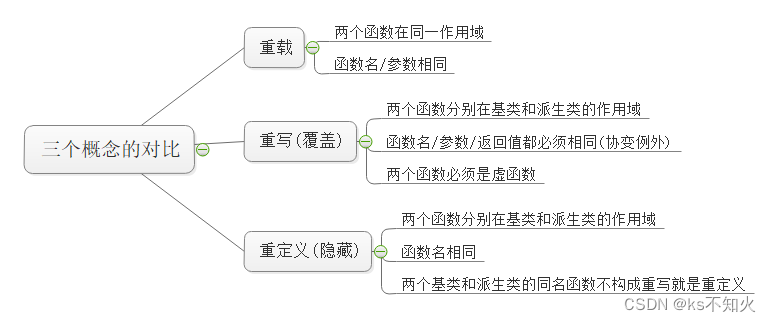
C++【多态】
文章目录1、多态的概念2、多态的定义及实现2-1、多态的构成条件2-2、虚函数2-3、虚函数的重写2-4 多态样例2-5、协变2-6、 析构函数与virtual2-7、函数重载、函数隐藏(重定义)与虚函数重写(覆盖)的对比2-8、override 和 final&…...

缓存预热、缓存雪崩、缓存击穿、缓存穿透,你真的了解吗?
缓存穿透、缓存击穿、缓存雪崩有什么区别,该如何解决? 1.缓存预热 1.1 问题描述 请求数量较高,大量的请求过来之后都需要去从缓存中获取数据,但是缓存中又没有,此时从数据库中查找数据然后将数据再存入缓存…...
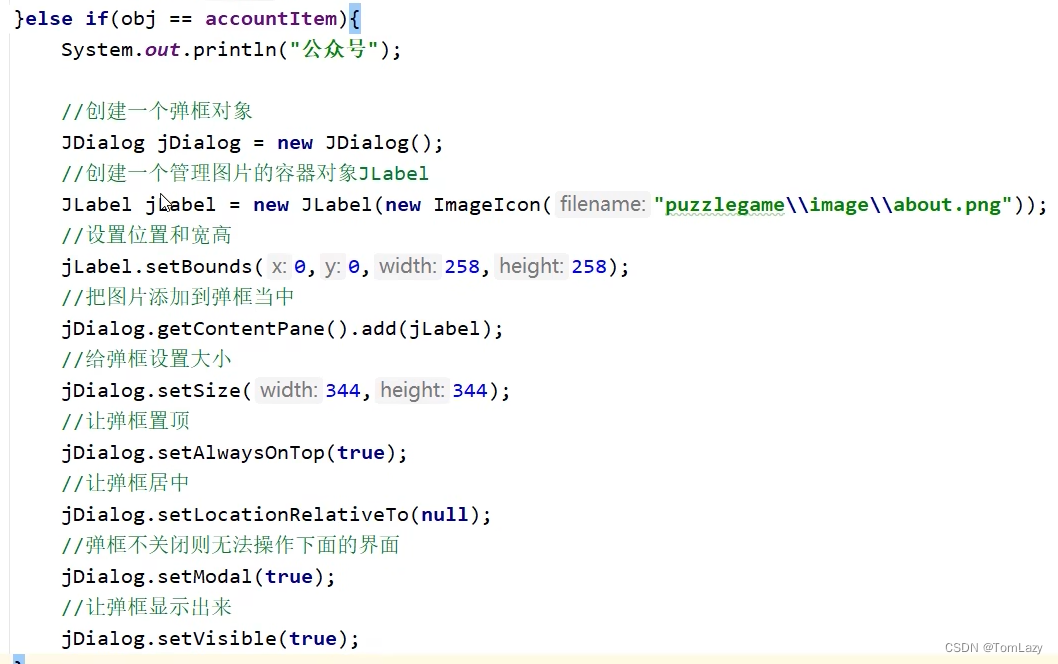
【Java基础】018 -- 面向对象阶段项目上(拼图小游戏)
目录 拼图小游戏(GUI) 一、主界面分析 1、练习一:创建主界面1 2、练习二:创建主界面2(JFrame) 3、练习三:在游戏界面中添加菜单(JMenuBar) ①、菜单的制作 4、添加图片&a…...
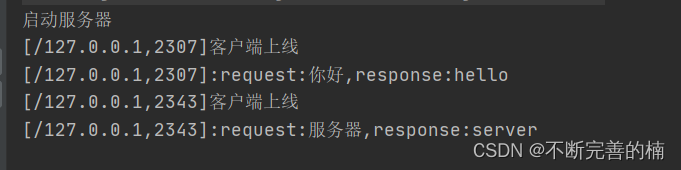
【网络~】
网络一级目录二、socket套接字三、UDP数据报套接字四、TCP流套接字一级目录 1.局域网、广域网 2.IP地址是什么? IP地址是标识主机在网络上的地址 IP地址是如何组成的? 点分十进制,将32位分为四个部分,每个部分一个字节ÿ…...

手写JavaScript中的call、bind、apply方法
手写JavaScript中的call、bind、apply方法 call方法 call() 方法使用一个指定的 this 值和单独给出的一个或多个参数来调用一个函数。 function Product(name, price) {this.name name;this.price price; }function Food(name, price) {Product.call(this, name, price);t…...

JAVA练习46-将有序数组转换为二叉搜索树
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 提示:这里可以添加本文要记录的大概内容: 2月10日练习内容 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目-…...
linux(centos7.6)docker
官方文档:https://docs.docker.com/engine/install/centos/1安装之前删除旧版本的docker2安装yum install-y yum-utils3配置yum源 不用官网的外国下载太慢 推荐阿里云yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.r…...

微信小程序滚动穿透问题
文章目录1、catchtouchmove"true"2、page-meta3、wx.setPageStyle做小程序的开发业务中,经常会使用弹窗,当弹窗里的内容过多时,要滚动查看,然后经常会遇到滚动弹窗,弹窗底下页面也跟着滚。解决思路ÿ…...
安全—06day
负载均衡反向代理下的webshell上传负载均衡负载均衡下webshell上传的四大难点难点一:需要在每一台节点的相同位置上传相同内容的webshell难点二:无法预测下一次请求是哪一台机器去执行难点三:当我们需要上传一些工具时,麻烦来了&a…...

PostgreSQL入门
PostgreSQL入门 简介 PostgreSQL是以加州大学伯克利分校计算机系开发的POSTGRES, 版本 4.2为基础的对象关系型数据库管理系统(ORDBMS) 支持大部分SQL标准并且提供了许多现代特性 复杂查询外键触发器可更新视图事务完整性多版本并发控制 …...

自媒体人都在用的免费音效素材网站
视频剪辑、自媒体人必备的剪辑音效素材网站,免费下载,建议收藏! 1、菜鸟图库 音效素材下载_mp3音效大全 - 菜鸟图库 菜鸟图库是一个综合性素材网站,站内涵盖设计、图片、办公、视频、音效等素材。其中音效素材就有上千首…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
