手写JavaScript中的call、bind、apply方法
手写JavaScript中的call、bind、apply方法
call方法
call() 方法使用一个指定的 this 值和单独给出的一个或多个参数来调用一个函数。
function Product(name, price) {this.name = name;this.price = price;
}function Food(name, price) {Product.call(this, name, price);this.category = 'food';
}console.log(new Food('cheese', 5).name);
// Expected output: "cheese"重写我们的call方法
分析:
- 函数调用call方法,所以这个方法写在Function.prototype上面
- 获取调用call方法的函数,指定到传入的context上面(这里给定一个名称为 context.fn)
- 获取传入的参数,作为context.fn的入参
- 调用context.fn并返回运行结果
// 手写call方法Function.prototype.Mycall = function (ctx = window, ...rest) {if (!(this instanceof Function)) {console.error(`${this} is not a function`)return}ctx.fn = thisconst res = ctx.fn(...rest)delete ctx.fnreturn res}
apply方法
apply() 方法调用一个具有给定 this 值的函数,以及以一个数组(或一个类数组对象)的形式提供的参数。
const numbers = [5, 6, 2, 3, 7];const max = Math.max.apply(null, numbers);console.log(max);
// Expected output: 7const min = Math.min.apply(null, numbers);console.log(min);
// Expected output: 2
分析:
- 函数调用apply方法,所以这个方法写在Function.prototype上面
- 获取调用apply方法的函数,指定到传入的context上面(这里给定一个名称为 context.fn)
- 获取传入的参数,这里是一个数组的形式,作为context.fn的入参
- 调用context.fn并返回运行结果
// 手写apply方法Function.prototype.Myapply = function (ctx = window, arrParams = []) {if (!(this instanceof Function)) {console.error(`${this} is not a function`)return}ctx.fn = thisconst res = ctx.fn(...arrParams)delete ctx.fnreturn res}
bind方法
bind() 方法创建一个新的函数,在 bind() 被调用时,这个新函数的 this 被指定为 bind() 的第一个参数,而其余参数将作为新函数的参数,供调用时使用。
const module = {x: 42,getX: function() {return this.x;}
};const unboundGetX = module.getX;
console.log(unboundGetX()); // The function gets invoked at the global scope
// Expected output: undefinedconst boundGetX = unboundGetX.bind(module);
console.log(boundGetX());
// Expected output: 42
分析:
- 函数调用bind方法,所以这个方法写在Function.prototype上面
- 生成一个新的函数并返回
- 在返回的函数中,通过call或者apply方法,指定传入进来的context,并获取传入的参数,作为入参
// 手写bind方法Function.prototype.Mybind = function (ctx = window, ...rest) {if (!(this instanceof Function)) {console.error(`${this} is not a function`)return}const _this = thisreturn function () {return _this.call(ctx, ...rest)}}
相关文章:

手写JavaScript中的call、bind、apply方法
手写JavaScript中的call、bind、apply方法 call方法 call() 方法使用一个指定的 this 值和单独给出的一个或多个参数来调用一个函数。 function Product(name, price) {this.name name;this.price price; }function Food(name, price) {Product.call(this, name, price);t…...

JAVA练习46-将有序数组转换为二叉搜索树
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 提示:这里可以添加本文要记录的大概内容: 2月10日练习内容 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目-…...
linux(centos7.6)docker
官方文档:https://docs.docker.com/engine/install/centos/1安装之前删除旧版本的docker2安装yum install-y yum-utils3配置yum源 不用官网的外国下载太慢 推荐阿里云yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.r…...

微信小程序滚动穿透问题
文章目录1、catchtouchmove"true"2、page-meta3、wx.setPageStyle做小程序的开发业务中,经常会使用弹窗,当弹窗里的内容过多时,要滚动查看,然后经常会遇到滚动弹窗,弹窗底下页面也跟着滚。解决思路ÿ…...
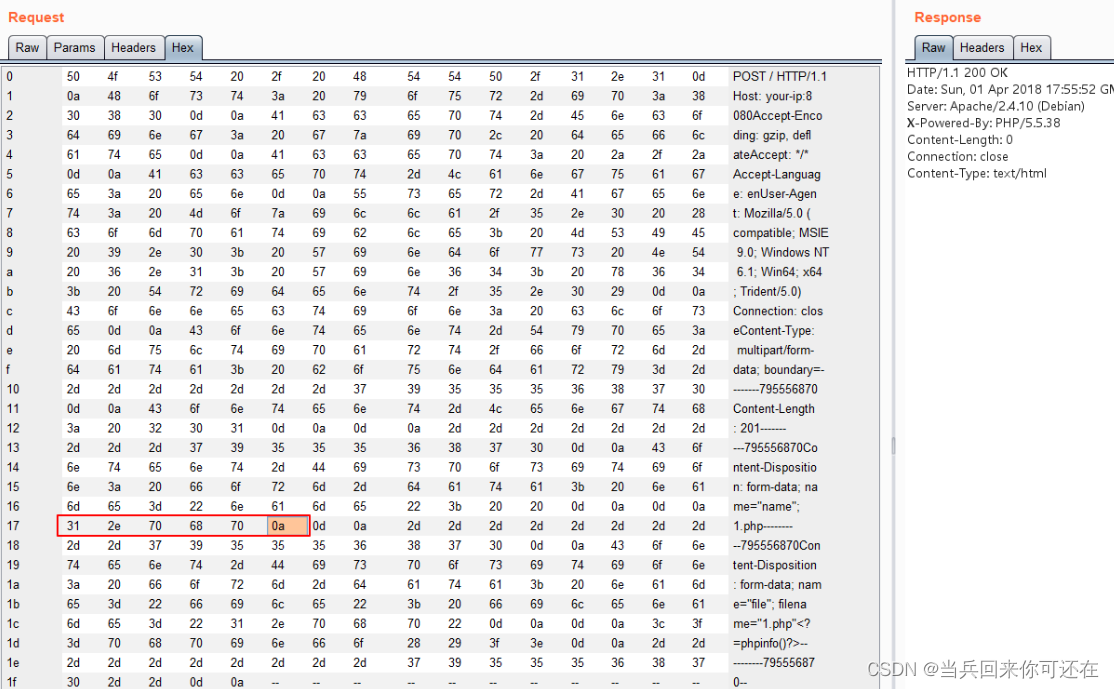
安全—06day
负载均衡反向代理下的webshell上传负载均衡负载均衡下webshell上传的四大难点难点一:需要在每一台节点的相同位置上传相同内容的webshell难点二:无法预测下一次请求是哪一台机器去执行难点三:当我们需要上传一些工具时,麻烦来了&a…...

PostgreSQL入门
PostgreSQL入门 简介 PostgreSQL是以加州大学伯克利分校计算机系开发的POSTGRES, 版本 4.2为基础的对象关系型数据库管理系统(ORDBMS) 支持大部分SQL标准并且提供了许多现代特性 复杂查询外键触发器可更新视图事务完整性多版本并发控制 …...

自媒体人都在用的免费音效素材网站
视频剪辑、自媒体人必备的剪辑音效素材网站,免费下载,建议收藏! 1、菜鸟图库 音效素材下载_mp3音效大全 - 菜鸟图库 菜鸟图库是一个综合性素材网站,站内涵盖设计、图片、办公、视频、音效等素材。其中音效素材就有上千首…...
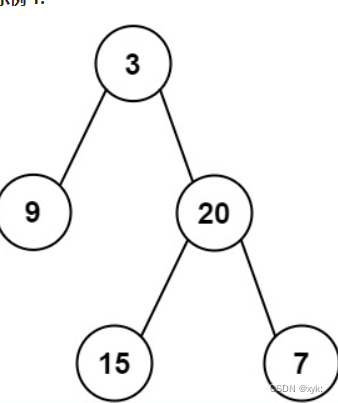
Java数据结构中二叉树的深度解析及常见OJ题
本篇文章讲述Java数据结构中关于二叉树相关知识及常见的二叉树OJ题做法讲解(包含非递归遍历二叉树) 目录 一、二叉树 1.1二叉树概念 1.2特殊的二叉树 1.3二叉树性质 1.4二叉树基本性质定理题 1.5二叉树遍历基本操作 1.6二叉树遍历的前中后非递归写法 1.7…...

算法顶级比赛汇总
可参赛的算法比赛 阿里云天池大数据竞赛 时间:每年各个季度很多类型都会出题(比赛总时间大概为两个月) 内容:各个类型的算法题都会出、奖金上万不等 形式:在线提交(提交后在线检查结果)、离线…...

Android MVI框架搭建与使用
MVI框架搭建与使用前言正文一、创建项目① 配置AndroidManifest.xml② 配置app的build.gradle二、网络请求① 生成数据类② 接口类③ 网络请求工具类三、意图与状态① 创建意图② 创建状态四、ViewModel① 创建存储库② 创建ViewModel③ 创建ViewModel工厂五、UI① 列表适配器②…...
第九节 使用设备树实现RGB 灯驱动
通过上一小节的学习,我们已经能够编写简单的设备树节点,并且使用常用的of 函数从设备树中获取我们想要的节点资源。这一小节我们带领大家使用设备树编写一个简单的RGB 灯驱动程序,加深对设备树的理解。 实验说明 本节实验使用到STM32MP1 开…...

Ubuntu 系统下Docker安装与使用
Ubuntu 系统下Docker安装与使用Docker安装与使用Docker安装安装环境准备工作系统要求卸载旧版本Ubuntu 14.04 可选内核模块Ubuntu 16.04 使用 APT 安装安装 Docker CE使用脚本自动安装启动 Docker CE建立 docker 用户组测试 Docker 是否安装正确镜像加速Docker使用拉取镜像创建…...
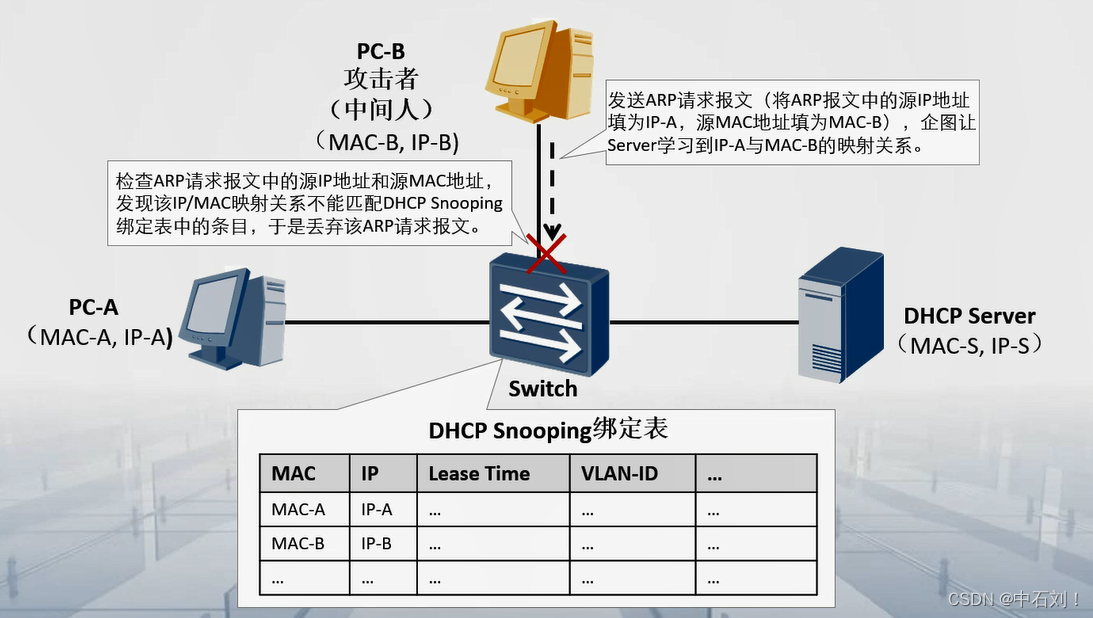
DHCP安全及防范
DHCP安全及防范DHCP面临的威胁DHCP饿死攻击仿冒DHCP Server攻击DHCP中间人攻击DHCP Snooping技术的出现DHCP Snooping防饿死攻击DHCP Snooping防止仿冒DHCP Server攻击DHCP Snooping防止中间人攻击DHCP Snooping防止仿冒DHCP报文攻击DHCP面临的威胁 网络攻击无处不在ÿ…...

【流畅的python】第一章 Python数据模型
文章目录第一章 Python 数据模型1.1 python风格的纸牌1.2 如何使用特殊方法-通过创建一个向量类的例子1.3 特殊方法汇总第一章 Python 数据模型 python最好的品质是一致性 python解释器碰到特殊句法时,会使用特殊方法去激活一些基本的对象操作 这些特殊的方法以两个…...
from文件突然全部变为类cs右击无法显示设计界面
右击也不显示查看设计器 工程文件 .csproj中将 <Compile Include"OperatorWindows\Connection.cs" /> <Compile Include"OperatorWindows\Connection.Designer.cs"> <DependentUpon>Connection.cs</DependentUpon> &…...

使用arthas中vmtool命令查看spring容器中对象的某个属性
场景: 线上环境我想查看spring中容器某个对象的属性值 vmtool命令 方式一: vmtool --action getInstances -c [类加载器的hash] --className [目标类全路径] --limit 10 -x 2 实例:查询该类的全部属性情况(该类是一个spri…...

四种幂等性解决方案
什么是幂等性? 幂等是一个数学与计算机学概念,在数学中某一元运算为幂等时,其作用在任一元素两次后会和其作用一次的结果相同。 在计算机中编程中,一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。 幂等…...

【Nacos】Nacos配置中心客户端配置更新源码分析
上文我们说了服务启动的时候从远程Nacos服务端拉取配置,这节我们来说下Nacos服务端配置的变动怎么实时通知到客户端,首先需要注册监听器。 注册监听器 NacosContextRefresher类会监听应用启动发布的ApplicationReadyEvent事件,然后进行配置…...

按钮防抖与节流-vue2
防抖与节流,应用场景有很多,例如:禁止重复提交数据的场景、搜索框输入搜索条件,待输入停止后再开始搜索。 防抖 点击button按钮,设置定时器,在规定的时间内再次点击会重置定时器重新计时,在规定…...

PyTorch学习笔记:nn.SmoothL1Loss——平滑L1损失
PyTorch学习笔记:nn.SmoothL1Loss——平滑L1损失 torch.nn.SmoothL1Loss(size_averageNone, reduceNone, reductionmean, beta1.0)功能:创建一个平滑后的L1L_1L1损失函数,即Smooth L1: l(x,y)L{l1,…,lN}Tl(x,y)L\{l_1,\dots,l…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
