【流畅的python】第一章 Python数据模型
文章目录
- 第一章 Python 数据模型
- 1.1 python风格的纸牌
- 1.2 如何使用特殊方法-通过创建一个向量类的例子
- 1.3 特殊方法汇总
第一章 Python 数据模型
python最好的品质是一致性
python解释器碰到特殊句法时,会使用特殊方法去激活一些基本的对象操作
这些特殊的方法以两个下划线开头,以两个下划线结尾,如__getitem__、__len__等
所谓的特殊句法,如通过下标访问列表,获取自定义类的元素的个数、重构操作符等等
__getitem__的读法: dunder getitem
随着学习的推进,对这一点的理解会逐渐加深......
我认为 ,特殊方法的实现,就是运算符的重构......
本章通过两个例子,来说明特殊用法
- 纸牌的例子
- 向量的例子
注:特殊方法是为了让编译器调用的,自己不需要调用。如没有obj.__len__()这种写法,应该使用len(obj)。此外, 不要自己想当然地随意添加特殊方法。
1.1 python风格的纸牌
创建一个纸牌类,实现
__getitem__和__len__两个特殊方法
代码如下
import collections
Card = collections.namedtuple('Card', ['rank', 'suit']) # 可以用来创建只有少数属性没有方法的类class FrenchDeck:ranks = [str(n) for n in range(2, 11)] + list('JQKA') # 创建一个list 存放2-Asuits = 'spades diamonds clubs hearts'.split() # 花色: 黑桃、红桃、方块、梅花# split默认为所有的空字符,包括空格、换行(\n)、制表符(\t)等。def __init__(self):self._cards = [Card(rank, suit)for suit in self.suitsfor rank in self.ranks]def __len__(self):return len(self._cards)def __getitem__(self, position):return self._cards[position]创建一个纸牌类之后,对上述类可以进行操作,代码如下:
def run_card():# 打印输出通过collections.namedtuple创建的类、以及类型test_card = Card('7', 'diamonds') print(test_card)print(type(test_card))deck = FrenchDeck()print(deck.ranks)print(deck.suits)print(len(deck)) # 获取FrenchDeck类中元素的个数 调用__len__print(deck[8]) # 根据下标获取FrenchDeck类中的元素 调用__getitem__# 通过python 内置的方法进行随机选择,而不必重新写一个对象from random import choiceprint(choice(deck)) # 随机从类中选择一个元素print(choice(deck))# 可以使用自动切片,因为__getitem__方法把[]操作给了self._cards,所以可以使用切片print(deck[:3]) # 下标为0、1、2print(deck[12::13]) # 抽出索引是12的牌, 步长为13,一次取1个# 可迭代,因为有__getitem__,可以进行迭代、逆迭代for card in deck:print(card)# 反向迭代for card in reversed(deck):print(card)# 由于是可迭代的,因此可以使用 in, # 集合类型没有实现__contains__方法,那么in运算符就会按顺序进行一次迭代搜索。print(Card('Q', 'hearts') in deck)print(Card('r', 'hearts') in deck)# 排序 因为可以迭代,因此可以进行排序for card in sorted(deck, key=spades_high): # spades_high为排序策略的方法名print(card)suit_values = dict(spades=3, hearts=2, diamonds=1, clubs=0) # 花色的大小定义
def spades_high(card):rank_value = FrenchDeck.ranks.index(card.rank) # 元素在类中的下标# print(card.rank +';'+ card.suit)# print('rank_value:'+str(rank_value))# print('len:'+ str(len(suit_values)))# print('*=' + str(rank_value * len(suit_values)))return rank_value * len(suit_values) + suit_values[card.suit]
FrenchDeck类隐式继承了Object类,但是功能却不是继承而来的
我们通过数据模型和一些合成来实现这些功能
通过实现__len__和__getitem__这两个特殊方法,FrenchDeck类就与python自有的序列数据类型一样,可以体现出python的核心语言特性
FrenchDeck类还可以用于标准库中random.choice、reversed、sorted这些函数
对合成的运用可以使得__len__、__getitem__的具体实现可以代理给self._cards这个列表
1.2 如何使用特殊方法-通过创建一个向量类的例子
实现一个二维向量类
Vector。
当然向量相关的运算在类中要进行实现,如输出(+)、取模(abs)、向量与数的乘法(*)、布尔判断(bool)
输出:通过内置函数
repr,可以把一个对象用字符串形式表示出来以便辨认,这就是"字符串表示形式"
repr是通过特殊方法__repr__来实现的,
如果没有实现这个特殊方法,<Vector object at 0x10e100070>
如果使用%来表示字符串,repr是通过%r来表示的
如果使用!来表示字符串,repr是通过!r来表示的
__repr__所返回的字符串应该准确、无歧义,并且尽可能表达出如何用代码创建出这个被打印的对象
__repr__和__str___的区别在于:后者是在str()被使用或者用print()打印一个对象时才被调用
由于python在调用str()时,如果没有发现__str__就会调用__repr__,因此优先创建__repr__
加法(
+):Vector(2, 3) + Vectotr(3, 5) = Vector(5, 8)
采用特殊方法__add__:这个特殊方法返回的是一个新的对象,被操作的两个对象原封不动。
向量与数的相乘(
*):Vector(2, 3) * 2 = Vector(4, 6)、Vector(4, 6) * (-2) = Vector(-8, -12)
采用特殊方法__mul__:这个特殊方法同__add__一样,都是返回一个新的对象。
取模运算(
abs):所谓的取模:就是元素的平方和再开方,即二范数 或 欧几里得范数
采用特殊方法__abs__
abs是一个内置函数,如果输入是整数或者浮点数,返回的是其绝对值;如果输入的是一个复数。返回的是复数的模
因此在Vector这个类中,通过调用abs,应当返回的是向量的模。
布尔运算(bool):这个函数只能返回
True、False
默认情况下,我们自己定义的类的实例总被认为是真的,除非这个类对__bool__或__len__有自己的实现,
bool(x)是调用x.__bool__()的结果,如果不存在__bool__,会调用__len__,如果返回0,bool就返回False,否则,返回True
Vector类的实现如下:
from math import hypot # hypot 是用来求欧几里得范数的class Vector:def __init__(self, x=0, y=0): # 定义了 x y 应该是整数类型self.x = xself.y = ydef __repr__(self): # __repr__ 中要使用 %r 保存原格式 %r可以用来获取对象各个属性的标准字符串表示形式return 'Vector(%r, %r)' % (self.x, self.y) # 此时输出的应该为 Vector(3, 4)def __abs__(self):return hypot(self.x, self.y) # 返回欧几里得范数 就是向量的模# 如果模是0 返回False 否则返回True# 法1# def __bool__(self):# return bool(abs(self))# 法2 更高效,省掉了abs到__abs__到平方再到平方根这些过程def __bool__(self):return bool(self.x or self.y) # or运算可能返回x或y本身的值,若x的值为真,则or返回x的值,否返回y的值def __add__(self, other):x = self.x + other.xy = self.y + other.yreturn Vector(x, y)def __mul__(self, scalar):return Vector(self.x * scalar, self.y * scalar)
对
Vector类的功能的调用,代码如下:
def run_vector():vector1 = Vector(3, 4)print('向量1=%r' % vector1)print('向量的模长= %f' % abs(vector1))vector2 = Vector(1, 2)print('向量2 = %r' % vector2)print('向量1 + 向量2 = %r' % (vector1 + vector2))# print('向量1 * 3 = %r' % (vector1 * 3)) # 数在后,向量在前,与__mul__一致print('向量1的bool = %r' % bool(vector1))
1.3 特殊方法汇总
python语法参考手册中的 Data Model列出了83个特殊方法的名字。下面列出概况。
下表的分类方式与官方文档不同
与运算符无关的特殊方法:
| 类别 | 方法名 |
|---|---|
| 字符串/字节序列表示形式 | __repr__、 __str__、 __format__、 __bytes__ |
| 数值转换 | __abs__、 __bool__、 __complex__、 __int__、 __float__、 __hash__、 __index__ |
| 集合模拟 | __len__、 __getitem_、 __seitem__、 __delitem__、 __contains__ |
| 迭代枚举 | __iter__、 __reversed__、 __next__ |
| 可调用模拟 | __call__ |
| 上下文管理 | __repr__、 __repr__ |
| 实例创建和销毁 | __new__、 __init__、 __del__ |
| 属性管理 | __getattr__、 __getattribute__、 __setattr__、 __delattr__、 __dir__ |
| 属性描述符 | __get__、 __set__、 __delete__ |
| 跟类相关的服务 | __prepare__、 __instancecheck__、 __subclasscheck__ |
跟运算法相关的特殊方法
| 类别 | 方法名 |
|---|---|
| 一元运算符 | __neg__ -、 __pos__ +、 __abs__ abs()、 |
| 比较运算符 | __lt__ <、 __le__ <=、 __eq__ ==、 __ne__ !=、 __gt__ >、 __ge__ >=、 |
| 算术运算符 | __add__ +、__sub__ -、 __mul__ *、__truediv__ /、 __floordiv__ //、 __mod__ %、 __divmod__ divmod()、__pow__ ** 或pow()、 __round__ round() |
| 反向算术运算符 | __radd__、 __rsub__、 __rmul__、 __rtruediv__、 __rfloordiv__、 __rmod__、 __rdivmod__ |
| 增量赋值算术运算符 | __iadd__、 __isub__、 __imul__、 __itruediv__、 __ifloordiv__、__imod__、 __ipow__ |
| 位运算符 | __invert__ ~、 __lshift__ <<、 __rshift__>>、 __and__ &、 __or__ |
| 反向位运算符 | __rlshift__、 __rrshift__、 __rand__、 __rxor__、 __ror__ |
| 增量赋值位运算符 | __ilshift__、 __irshift__、 __iand__、 __ixor__、 __ior__ |
增量赋值运算符:
a *= b
反向算术运算符,当两个操作数交换了前后位置,此时想要得到一致的结果,需要调用反向算术运算符
相关文章:

【流畅的python】第一章 Python数据模型
文章目录第一章 Python 数据模型1.1 python风格的纸牌1.2 如何使用特殊方法-通过创建一个向量类的例子1.3 特殊方法汇总第一章 Python 数据模型 python最好的品质是一致性 python解释器碰到特殊句法时,会使用特殊方法去激活一些基本的对象操作 这些特殊的方法以两个…...
from文件突然全部变为类cs右击无法显示设计界面
右击也不显示查看设计器 工程文件 .csproj中将 <Compile Include"OperatorWindows\Connection.cs" /> <Compile Include"OperatorWindows\Connection.Designer.cs"> <DependentUpon>Connection.cs</DependentUpon> &…...

使用arthas中vmtool命令查看spring容器中对象的某个属性
场景: 线上环境我想查看spring中容器某个对象的属性值 vmtool命令 方式一: vmtool --action getInstances -c [类加载器的hash] --className [目标类全路径] --limit 10 -x 2 实例:查询该类的全部属性情况(该类是一个spri…...

四种幂等性解决方案
什么是幂等性? 幂等是一个数学与计算机学概念,在数学中某一元运算为幂等时,其作用在任一元素两次后会和其作用一次的结果相同。 在计算机中编程中,一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。 幂等…...

【Nacos】Nacos配置中心客户端配置更新源码分析
上文我们说了服务启动的时候从远程Nacos服务端拉取配置,这节我们来说下Nacos服务端配置的变动怎么实时通知到客户端,首先需要注册监听器。 注册监听器 NacosContextRefresher类会监听应用启动发布的ApplicationReadyEvent事件,然后进行配置…...

按钮防抖与节流-vue2
防抖与节流,应用场景有很多,例如:禁止重复提交数据的场景、搜索框输入搜索条件,待输入停止后再开始搜索。 防抖 点击button按钮,设置定时器,在规定的时间内再次点击会重置定时器重新计时,在规定…...

PyTorch学习笔记:nn.SmoothL1Loss——平滑L1损失
PyTorch学习笔记:nn.SmoothL1Loss——平滑L1损失 torch.nn.SmoothL1Loss(size_averageNone, reduceNone, reductionmean, beta1.0)功能:创建一个平滑后的L1L_1L1损失函数,即Smooth L1: l(x,y)L{l1,…,lN}Tl(x,y)L\{l_1,\dots,l…...
2年时间,涨薪20k,想拿高薪还真不能老老实实的工作...
2016年开始了我的测试生活。 2016年刚到公司的时候,我做的是测试工程师。做测试工程师是我对自己的职业规划。说实话,我能得到这份工作真的很高兴。 来公司的第一个星期,因为有一个项目缺人,所以部门经理提前结束了我的考核期&a…...

Spark - Spark SQL中RBO, CBO与AQE简单介绍
Spark SQL核心是Catalyst, Catalyst执行流程主要分4个阶段, 语句解析, 逻辑计划与优化, 物理计划与优化, 代码生成 前三个阶段都由Catalyst负责, 其中, 逻辑计划的优化采用RBO思路, 物理计划的优化采用CBO思路 RBO (Rule Based Optimization) 基于规则优化, 通过一系列预定好…...

NeurIPS/ICLR/ICML AI三大会国内高校和企业近年中稿量完整统计
点击文末公众号卡片,找对地方,轻松参会。 近日,有群友转发了一张网图,统计了近年来中国所有单位在NeurIPS、ICLR、ICML论文情况。原图如下: 中稿数100: 清华(1) 北大(2) 占比:22.6%。 累计数…...
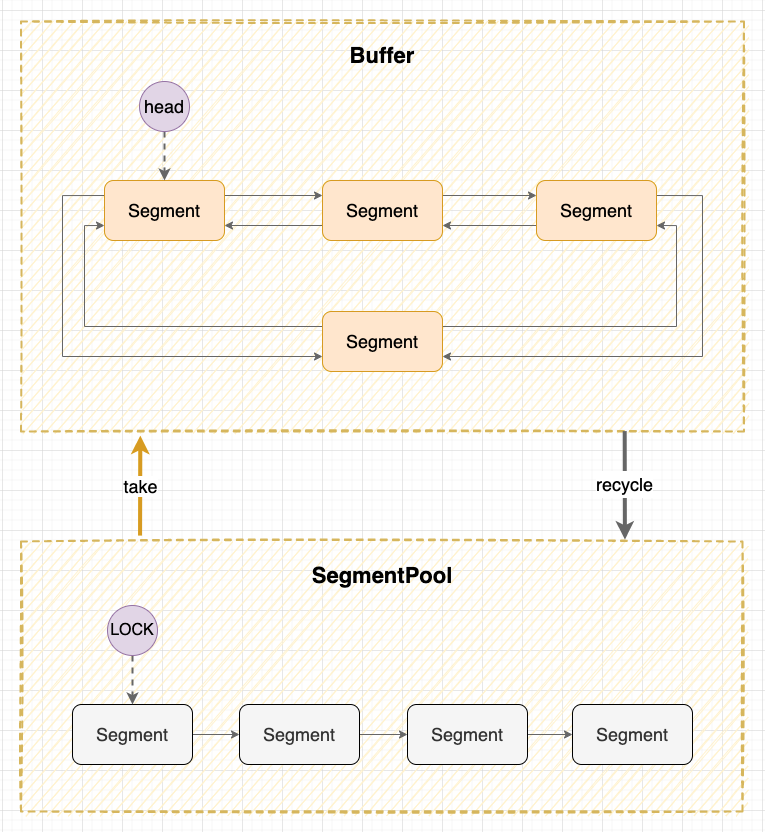
Android IO 框架 Okio 的实现原理,到底哪里 OK?
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 前言 大家好,我是小彭。 今天,我们来讨论一个 Square 开源的 I/O 框架 Okio,我们最开始接触到 Okio 框架还是源于 Square 家的 OkHttp 网络…...

一文讲解Linux 设备模型 kobject,kset
设备驱动模型 面试的时候,有面试官会问,什么是Linux 设备驱动模型?你要怎么回答? 这个问题,突然这么一问,可能你会愣住不知道怎么回答,因为Linux 设备驱动模型是一个比较整体的概念࿰…...

linux配置密码过期的安全策略(/etc/login.defs的解读)
长期不更换密码很容易导致密码被破解,而linux的密码过期安全策略主要在/etc/login.defs中配置。一、/etc/login.defs文件的参数解读1、/etc/login.defs文件的内容示例[rootlocalhost ~]# cat /etc/login.defs # # Please note that the parameters in this configur…...

c_character_string 字符串----我认真的弄明白了,也希望你们也是。
字符串 1. 字符串长度strlen 1.1strlen 函数介绍 size_t strlen ( const char * str );strlen ——string length strlen 的头文件是 #include <string.h> 参数指向的字符串必须要以 ‘\0’ 结束。 strlen 是求字符串长度的函数,统计的是字符串中\0之前出现…...
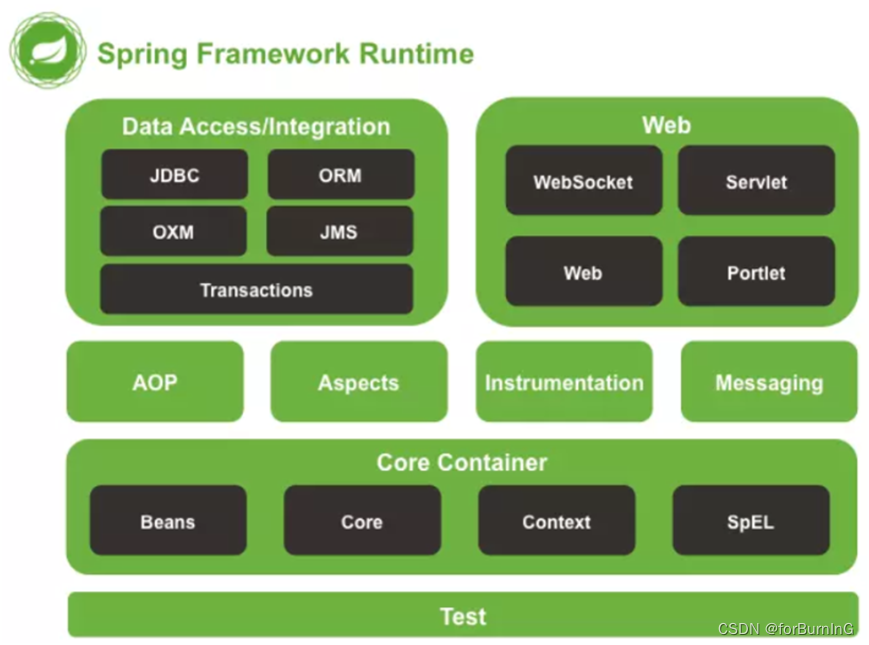
spring面试题 一
一、为了降低Java开发的复杂性,Spring采取了那4种关键策略 基于POJO的轻量级和最小侵入性编程; 通过依赖注入和面向接口实现松耦合; 基于切面和惯例进行声明式编程; 通过切面和模板减少样板式代码。 二、Spring框架的核心&am…...

C++中char *,char a[ ]的特殊应用
1.数组的本质 数组是多个元素的集合,在内存中分布在地址相连的单元中,所以可以通过其下标访问不同单元的元素。 2.指针 指针也是一种变量,只不过它的内存单元中保存的是一个标识其他位置的地址。 3.字符串常量的本质是它的第一个字符的地…...
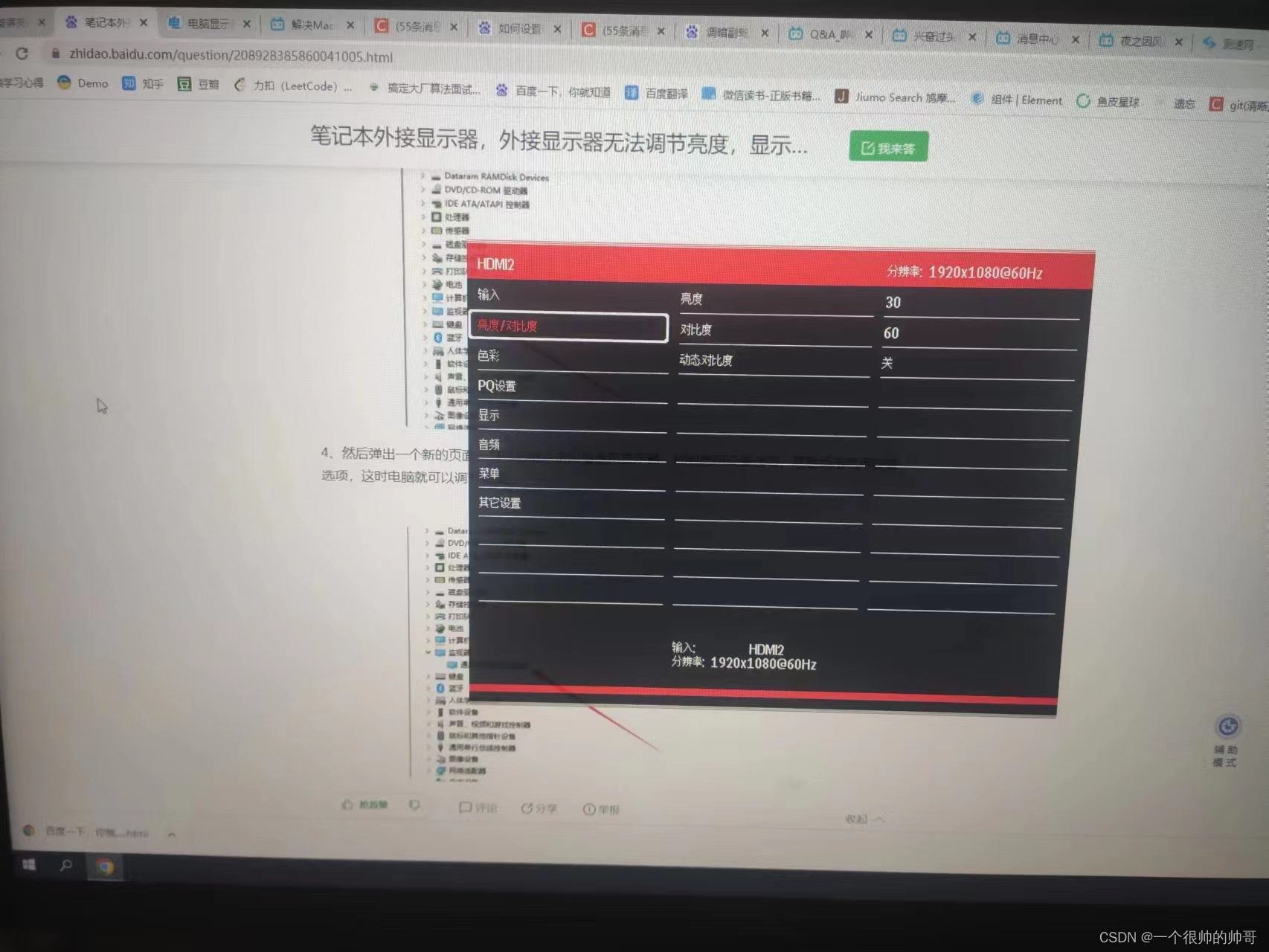
【Windows10】电脑副屏无法调节屏幕亮度?解决方法
先说下情况,本人对显示器不太懂,属于小白 这个副屏无法调节的问题出现也已经很久了,但是之前亮度适合就无所谓,今天突然按了之后很亮,于是就找问题。 第一步,我直接百度,遇事不决,百…...

Paper简读 - ProGen2: Exploring the Boundaries of Protein Language Models
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/128976102 ProGen2: Exploring the Boundaries of Protein Language Models ProGen2:探索蛋白质语言模型的边界Cumulative density:累积密度 Ligand:在生…...

leaflet 加载WKT数据(示例代码050)
第050个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中加载WKT文件,将图形显示在地图上。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果; 注意如果OpenStreetMap无法加载,请加载其他来练习 文章目录 示例效果配置方式示例源代码(共67行…...

设计模式-组合模式和建筑者模式详解
一. 组合模式 1. 背景 在现实生活中,存在很多“部分-整体”的关系,例如,大学中的部门与学院、总公司中的部门与分公司、学习用品中的书与书包、生活用品中的衣月艮与衣柜以及厨房中的锅碗瓢盆等。在软件开发中也是这样,例如&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
