【数据结构】空间复杂度

🚀write in front🚀
📜所属专栏:初阶数据结构
🛰️博客主页:睿睿的博客主页
🛰️代码仓库:🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论,是对我最大的激励和支持!!!
关注我,关注我,关注我,你们将会看到更多的优质内容!!

文章目录
- 前言:
- 一.空间复杂度
- 栗子1:
- 栗子2:
- 栗子3:
- 栗子4:
- 二.常见复杂度对比
- 总结:
前言:
上一篇博客我们讲解了时间复杂度的相关知识,那么时间有复杂度,可以有复杂度吗?下面我们就来了解一下空间复杂度的相关知识!
一.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间(变量个数)来确定。
常数个变量的复杂度:O(n)
栗子1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
空间复杂度为O(1)
因为调用了常数个常数个额外空间。
栗子2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}
空间复杂度为O(n)
动态开辟了n+1个空间
栗子3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
空间复杂度为O(n)
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。
栗子4:
// 计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
空间复杂度为O(N)
很多小伙伴可能会以为空间复杂度为O(2^N),但是实则不是。我们先来看看下面的图:

递归是有先后顺序,并不是同一时间内同时递归的,所以递归会按先后顺序依次递归,顺序就像如图所示的1 2 3 4 5 6……这样递归。所以开辟的空间最多为N个,随后返回空间。所以空间复杂度为O(N)。
二.常见复杂度对比
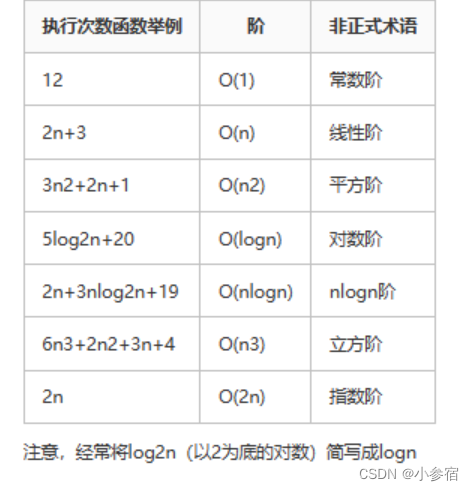
总结:
这就是时间复杂度和空间复杂度的全部知识!希望对大家有所帮助
更新不易,辛苦各位小伙伴们动动小手,👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!
专栏订阅:
每日一题
c语言学习
算法
智力题
初阶数据结构
更新不易,辛苦各位小伙伴们动动小手,👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要!最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!

相关文章:

【数据结构】空间复杂度
🚀write in front🚀 📜所属专栏:初阶数据结构 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对…...

湖南中创教育提醒校外培训留意这几点,避免维权
校外教育培训机构是市场经济发展的必然产物,有需求就有市场,这个无可厚非。而校外教育培训机构的火热,正是反映出人民群众对教育发展的需求在不断增强。 培训机构分类中有面对大学生参加公务员招考、教师考编等考证考试的培训机构࿱…...

docker 配置私有/本地镜像仓库
docker 配置私有/本地镜像仓库docker pull registry mkdir -p /usr/local/docker/registry-data docker tag registry 192.168.28.132:5000/registry docker run -di -p 5000:5000 --namelocal_registry --restartalways --privilegedtrue --log-drivernone -v /usr/local/d…...

每日学术速递2.23
Subjects: Robotics 1.On discrete symmetries of robotics systems: A group-theoretic and data-driven analysis 标题:关于机器人系统的离散对称性:群论和数据驱动分析 作者:Daniel Ordonez-Apraez, Mario Martin, Antonio Agudo, F…...

LeetCode 232. 用栈实现队列
LeetCode 232. 用栈实现队列 难度:easy\color{Green}{easy}easy 题目描述 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(pushpushpush、poppoppop、peekpeekpeek、emptyemptyempty): 实现 MyQueueM…...

AI算法创新赛-人车目标检测竞赛总结04
队伍:AI000038 小组成员:杨志强,林松 1. 算法介绍 1.1 相关工作 当前流行的目标检测算法主要分为三种,一阶段算法:SSD,FCOS,Scaled,YOLO系列等;二阶段算法:…...

【C语言进阶】动态内存管理详解与常见动态内存错误以及柔性数组使用与介绍
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C语言进阶 🎯长路漫漫浩浩,万事皆有期待 文章目录1.动态内存1.1 概述…...

【C++】string的模拟实现
文章目录1. string的模拟实现1.构造函数使用new开辟空间优化成全缺省的构造函数2. C_str3. operator[]4.拷贝构造浅拷贝深拷贝5. 赋值三种情况6. 迭代器7.比较(ASCII值)大小8. reserve(扩容)9. push_back(尾插字符)10. append(尾插字符串)11. (字符/字符串)12. insert在pos位置…...
前端借助Canvas实现压缩base64图片两种方法
一、具体代码 1、利用canvas压缩图片方法一 // 第一种压缩图片方法(图片base64,图片类型,压缩比例,回调函数)// 图片类型是指 image/png、image/jpeg、image/webp(仅Chrome支持)// 该方法对以上三种图片类型都适用 压缩结果的图片base64与原类型相同// …...
用ChatGPT生成Excel公式,太方便了
ChatGPT 自去年 11 月 30 日 OpenAI 重磅推出以来,这款 AI 聊天机器人迅速成为 AI 界的「当红炸子鸡」。一经发布,不少网友更是痴迷到通宵熬夜和它对话聊天,就为了探究 ChatGPT 的应用天花板在哪里,经过试探不少人发现,…...
【Kubernetes 企业项目实战】09、Rancher 2.6 管理 k8s-v1.23 及以上版本高可用集群
目录 一、Rancher 介绍 1.1Rancher简介 1.2 Rancher 和 k8s 的区别 1.3 Rancher 企业使用案例 二、安装 Rancher 2.1 初始化环境 2.2 安装 Rancher 2.3 登录 Rancher 平台 三、通过 Rancher 管理已存在的 k8s 集群 3.1 配置 rancher 3.2 导入 k8s 四、通过 Ranc…...
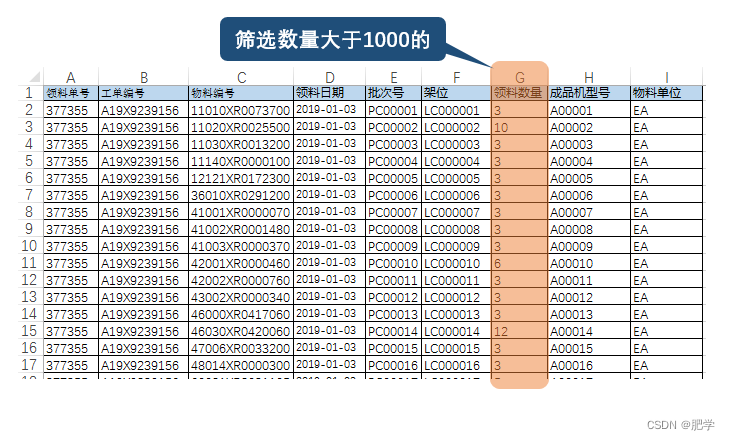
在Excel中按条件筛选数据并存入新的表
案例 老板想要看去年每月领料数量大于1000的数据。手动筛选并复制粘贴出来,需要重复操作12次,实在太麻烦了,还是让Python来做吧。磨刀不误砍柴工,先整理一下思路: 1读取原表,将数量大于1000的数据所对应的行整行提取(如同在excel表中按数字筛选大于1000的) 2将提取的数…...

【面试题】MySQL索引相关知识点
1.什么是索引 索引是存储引擎快速查找记录的一种数据结构,就类似书的目录,通过目录可以快速的查找到想要查找的内容 2.索引的特点 特点:索引是基于数据引擎的,不同的数据引擎实现索引的方式不一定相同 好处:通过索引…...
MySQL索引类型及原理?一文读懂
一、什么是MySQL索引? MySQL索引是一种数据结构,用于提高数据库查询的性能。它类似于一本书的目录,通过在表中存储指向数据行的引用,使得查询数据的速度更快。 在MySQL中,索引通常是在表上定义的,它们可以…...
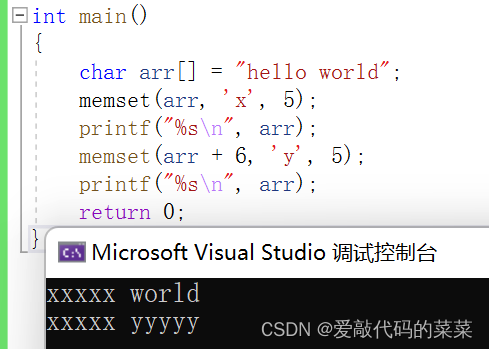
【C语言】字符分类函数+内存函数
目录 1.字符函数 1.1字符分类函数 1.2.字符转换函数 //统一字符串中的大小写 2.内存处理函数 2.1内存拷贝函数memcpy //模拟实现memcpy 2.2内存移动函数memmove //模拟实现memmove 2.3内存比较函数memcmp 2.4内存设置函数memset 1.字符函数 1.1字符分类函数 头文…...

高通平台开发系列讲解(SIM卡篇)SIM卡基础概念
文章目录 一、SIM卡基本定义二、卡的类型三、SIM卡的作用三、SIM卡基本硬件结构四、SIM卡的内部物理单元五、卡文件系统沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍SIM的相关组件。 一、SIM卡基本定义 SIM卡是一种智能卡(ICC Card/UICC Card) SIM…...

记录一次ubuntu下配置ssh登录出现的问题
现象描述: 1. 配置完服务器端公钥和本地的私钥之后,ssh登录始终会让输入密码,用ssh -vvv rootip 查看发现发送密钥之后就没反应了。 本机debug info: debug1: Trying private key: C:\Users\wangc/.ssh/id_xxxx (私钥文件) debug3…...

深度剖析数据在内存中的存储(下)(适合初学者)
上篇讲解了整形在内存中的存储方式,这篇文章就来继续讲解浮点数在内存中的存储方式。 上篇地址: (5条消息) 深度剖析数据在内存中的存储(上)_陈大大陈的博客-CSDN博客 目录: 3.浮点型在内存中的存储 3.1.浮点数的…...
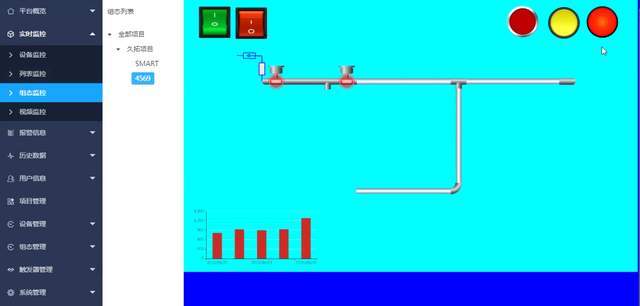
智慧物联网系统源码:一个用于数据的收集、处理、可视化、设备管理、设备预警、报警的平台
项目简介: 一个用于数据的收集、处理、可视化、设备管理、设备预警、报警的平台,通过平台将所有设备连接起来,为上层应用提供设备的管理、数据收集、远程控制等核心物联网功能。 支持支持远程对设备进行实时监控、故障排查、远程控制&#…...

2023年,拥有软考证书在这些地区可以领取福利补贴
众所周知,软考的含金量很高,比如可以入户、领取技能补贴、抵扣个税、以考代评、招投标加分,入专家库… 今天小编给大家收集了拥有软考证书可以领取软考福利的地区,希望对大家有所帮助! 【深圳】 入户 ①核准类入户:…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
