学习记忆——数学篇——案例——算术——整除特点

理解记忆法
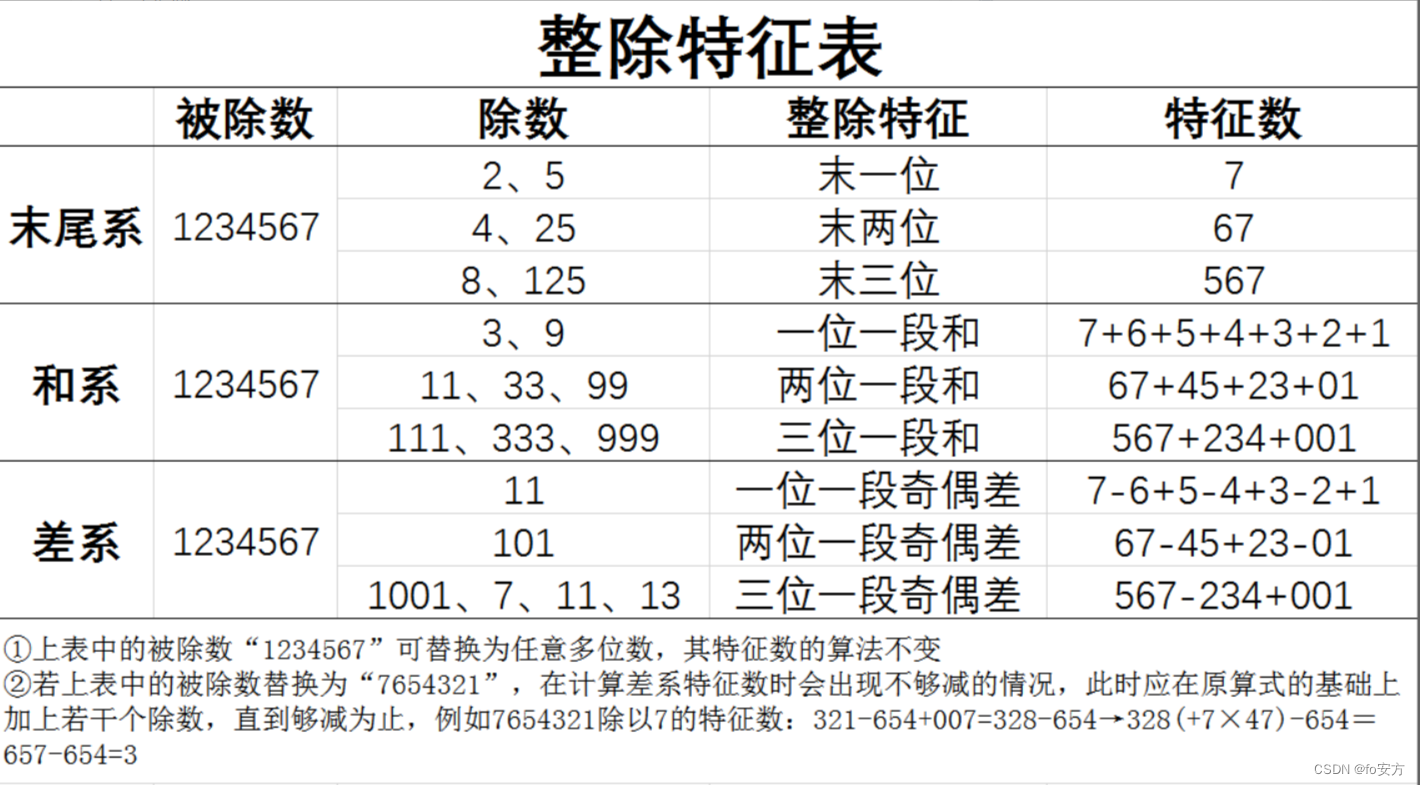
对于数的整除特征大家都比较熟悉:比如4看后两位(因为100是4的倍数),8看后三位(因为1000是8的倍数),5末尾是0或5,3与9看各位数字和等等,今天重点研究一下3,9,7,11,13的整除特征(重点是三位截断法的原理)。继续用字母来代替数来推导公式,弄清原理又锻炼代数与证明问题能力。
①3,9的整除特征(各位数字和)
设三位数abc(a,b,c等代表0-9的数字,以下同样),用位值原理拆开
100a+10b+c
=(99+1)a+(9+1)b+c
=99a+9b+a+b+c
由于前两项都是9的倍数,不影响除以9的余数,所以a+b+c就是这个数除以9的余数。如果除以9余0,那么这个数就是9的倍数。
②11的整除特征(奇位数字和与偶位数字和的差)
把一个数由右边向左边数,如果奇位上数字和与偶位上数字和的差,是11的倍数(包括0),那么这个数就是11的倍数。
首先10的奇数次方减去1就是11的倍数,例如10000-1=9999,100-1=99
其次10的偶数次方加上1也是11的倍数,例如1000+1=1001,10+1=11
设五位数abcde,用位值原理拆开
10000a+1000b+100c+10d+e=9999a+1001b+99c+11d+a-b+c-d+e
前4项都是11的倍数,不影响除以11的余数。所以如果a-b+c-d+e是11的倍数,那么这个数就是11的倍数。
(由于是减法,可能出现负数,可以加上11的倍数变成非负的再判断;或者用偶数位和减去奇数位和,用它们的差判断就可以)
③三位截断法(后三位截断作差)的原理(7,11,13)
这种方法利用1001=7×11×13
设六位数abcdef,用位值原理拆开
1000abc+def=1001abc-abc+def
第一项是1001的倍数,可以不考虑它。
只看def-abc即可(如果为负数,可以用abc-def来判断,即def与abc的差)
例如def与abc的差是13的倍数,那么abcdef就是13的倍数。
如果位数比较大可以多截几次
例:判断593654321是否是7,11,13的倍数。
593654-321=593333;593-333=260;
因为260不是7,11的倍数,
所以593654321不是7,11的倍数。
因为260是13的倍数,
所以593654321就是13的倍数。

相关文章:

学习记忆——数学篇——案例——算术——整除特点
理解记忆法 对于数的整除特征大家都比较熟悉:比如4看后两位(因为100是4的倍数),8看后三位(因为1000是8的倍数),5末尾是0或5,3与9看各位数字和等等,今天重点研究一下3,9,…...

PHP8中的魔术方法-PHP8知识详解
在PHP 8中,魔术方法是一种特殊的方法,它们以两个下划线(__)开头。魔术方法允许您定义类的行为,例如创建对象、调用其他方法或访问和修改类的属性。以下是一些常见的魔术方法: __construct(): 类的构造函数…...

[图论]哈尔滨工业大学(哈工大 HIT)学习笔记23-31
视频来源:4.1.1 背景_哔哩哔哩_bilibili 目录 1. 哈密顿图 1.1. 背景 1.2. 哈氏图 2. 邻接矩阵/邻接表 3. 关联矩阵 3.1. 定义 4. 带权图 1. 哈密顿图 1.1. 背景 (1)以地球为建模,从一个大城市开始遍历其他大城市并且返回…...

Nginx+Keepalived实现服务高可用
Nginx 和 Keepalived 是常用于构建高可用性(High Availability)架构的工具。Nginx 是一款高性能的Web服务器和反向代理服务器,而Keepalived则提供了对Nginx服务的健康状态监测和故障切换功能。 下载Nginx 在服务器1和服务器2分别下载nginx …...
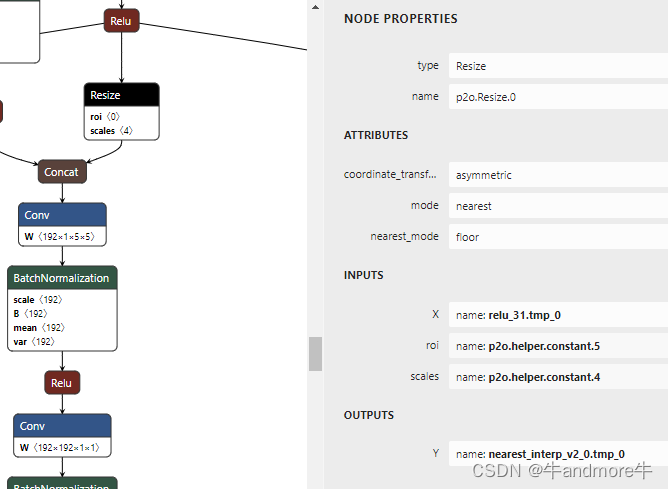
picodet onnx转其它芯片支持格式时遇到
文章目录 报错信息解决方法两模型精度对比 报错信息 报错信息为: Upsample(resize) Resize_0 not support attribute coordinate_transformation_mode:half_pixel. 解决方法 整个模型转换过程是:paddle 动态模型转成静态,再用paddle2onnx…...

【学习笔记】CF704B Ant Man
智商不够啊,咋想到贪心的😅 非常经典的贪心模型🤔 首先,从小到大将每个 i i i插入到排列中,用 D P DP DP记录还有多少个位置可以插入,可以通过钦定新插入的位置左右两边是否继续插入数来提前计算贡献。注…...

SQLines数据迁移工具
Data and Analytics Platform Migration - SQLines Tools SQLines提供的工具可以帮助您在不同的数据库平台之间传输数据、转换数据库模式(DDL)、视图、存储过程、包、用户定义函数(udf)、触发器、SQL查询和SQL脚本。 SQLines SQL Converter OverviewCommand LineConfigurati…...
)
pkl文件与打开(使用numpy和pickle)
文章目录 1. 什么是pkl文件2. 如何打开?Reference 1. 什么是pkl文件 1)python中有一种存储方式,可以存储为.pkl文件。 2)该存储方式,可以将python项目过程中用到的一些暂时变量、或者需要提取、暂存的字符串、列表、…...

3d渲染农场全面升级,好用的渲染平台值得了解
什么是渲染农场? 渲染农场是专门从事 3D 渲染的大型机器集合,称为渲染节点,这些机器组合在一起执行一项任务(渲染 3D 帧和动画)。通过将渲染工作分配给数百台机器,可以显着减少渲染时间,从而使…...

1.5 JAVA程序运行的机制
**1.5 Java程序的运行机制** --- **简介:** Java程序的运行涉及两个主要步骤:编译和运行。这种机制确保了Java的跨平台特性。 **主要内容:** 1. **Java程序的执行过程**: - **编译**:首先,扩展名为.jav…...

基于FPGA的拔河游戏设计
基于FPGA的拔河游戏机 设计内容: (1)拔河游戏机需要11个发光二极管排成一行,开机 后只有中间一个亮点,作为拔河的中间线。 游戏双方 各持一个按键,迅速且不断地按动产生脉冲,哪方按 得快,亮点就向哪方移动, 每按一次,亮点移动一次。 移到任一方二极管的终端,该方就…...
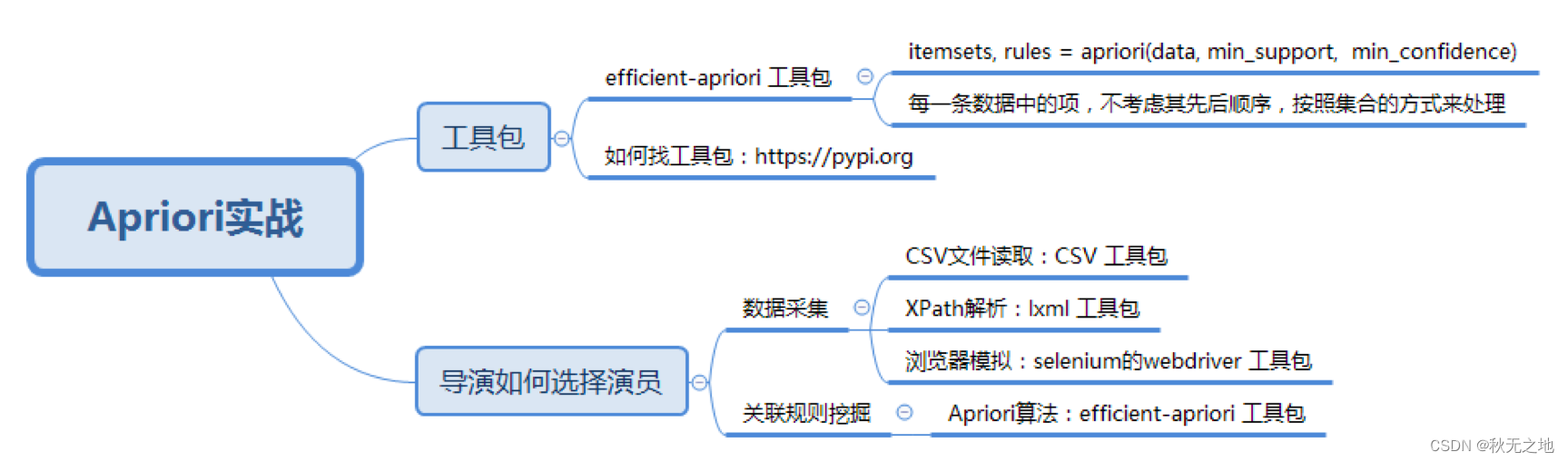
关联规则挖掘(下):数据分析 | 数据挖掘 | 十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

8、【Qlib】【主要组件】预测模型:模型训练和预测
8、【主要组件】预测模型:模型训练和预测 简介基本类Example简介 预测模型(Forecast Model)旨在对股票做出预测评分。用户可以通过 qrun 在自动化工作流中使用预测模型。 由于 Qlib 中的组件设计成了松耦合方式,预测模型也可以作为一个独立模块使用。 基本类 Qlib 提供了…...

kettle安装
kettle安装 安装java环境 mkdir /data/java ln -s /data/java/ /opt/ cd /opt/javatar zxvf jdk-8u171-linux-x64.tar.gz#java export JAVA_HOME/opt/java/jdk1.8.0_171 export JRE_HOME$JAVA_HOME/jre export CLASSPATH$JAVA_HOME/lib:$JRE_HOME/lib:$CLASSPATH export PATH$J…...

基于生物地理学优化的BP神经网络(分类应用) - 附代码
基于生物地理学优化的BP神经网络(分类应用) - 附代码 文章目录 基于生物地理学优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.生物地理学优化BP神经网络3.1 BP神经网络参数设置3.2 生物地理学算法应用 4…...
第二证券:买基金1w一个月能赚多少?
跟着经济的开展和出资观念的改动,越来越多的人开始出资基金,购买基金已成为普遍且盛行的出资方式之一。在这个商场中,人们最重视的问题莫过于“买基金1w一个月能赚多少?”本文将从多个角度分析这一问题,协助出资者更全…...

蓝桥杯每日一题2023.10.7
跑步锻炼 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 简单枚举,对于2的情况特判即可 #include<bits/stdc.h> using namespace std; int num, ans, flag; int m[13] {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; bool is_ren(int n) {if((n %…...
Linux 系统为何产生大量的 core 文件?
Author:rab 目录 一、问题分析二、解决方案扩展 一、问题分析 上一篇刚讲到《Docker 配置基础优化》,这里再补充一下。就在中秋国庆这段小长假里,接收到了线上服务器磁盘告警通知,线上服务器架构是一个 Docker Swarm 集群&#x…...
Web_python_template_injection SSTI printer方法
这题挺简单的 就是记录一下不同方法的rce python_template_injection ssti了 {{.__class__.__mro__[2].__subclasses__()}} 然后用脚本跑可以知道是 71 {{.__class__.__mro__[2].__subclasses__()[71]}} 然后直接 init {{.__class__.__mro__[2].__subclasses__()[71].__i…...
)
TCP/IP网络江湖——江湖导航(网络层上篇)
目录 一、引言 二、IP地址与路由 三、IP协议与数据包转发 3.1 IP协议:网络江湖的规矩...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
