Leetcode901-股票价格跨度
一、前言
本题基于leetcode901股票价格趋势这道题,说一下通过java解决的一些方法。并且解释一下笔者写这道题之前的想法和一些自己遇到的错误。需要注意的是,该题最多调用 next 方法 10^4 次,一般出现该提示说明需要注意时间复杂度。
二、解决思路
①栈排序(存在超出时间限制问题)
其实笔者做这道题之前并不知道单调栈这一东西,第一时间想到的是很像之前做过的和栈相关的一道题–栈排序,毕竟都是类似按照某一顺序对栈元素进行排序。需要借用辅助栈,而考虑到它需要计算的是连续天数,不是一个简单的排序。
拿这道题给的示例输入来说:
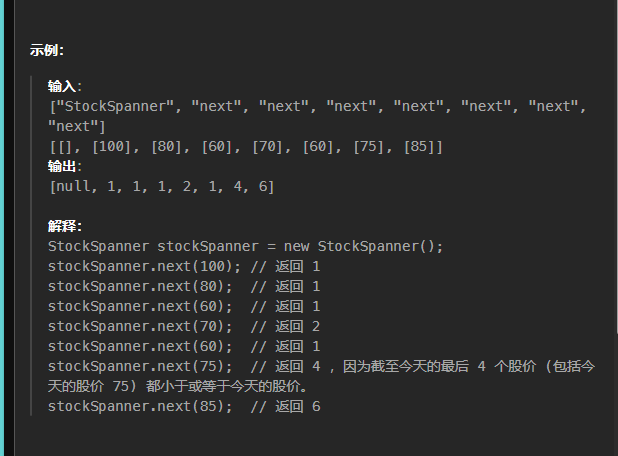
思路就是如果是空栈,那么我们直接放就好。
而当不是空栈时,此时通过price和栈顶元素的差值区分情况:
①小于0:
说明price要小,那么我们直接入栈,然后由于此时栈肯定没有比price更小的元素,所以只有它自己,return 1即可
②大于等于0:
说明此时price要大于栈顶元素,由于它要的是最大连续日数(从今天开始往回数,包括今天),那么我必须得保持入栈的一个顺序,否则就不是连续的,而是一个比当前price要小的所有天数这样一个结果。
那么怎样处理呢,我们可以先将该price入辅助栈,然后再从栈顶遍历,将小于等于当前price的栈元素弹出push到辅助栈中。此时记录辅助栈的size就是我们要返回的最大连续天数,最后再将辅助栈一次push到我们的主栈中即可。
我这边画一个图:
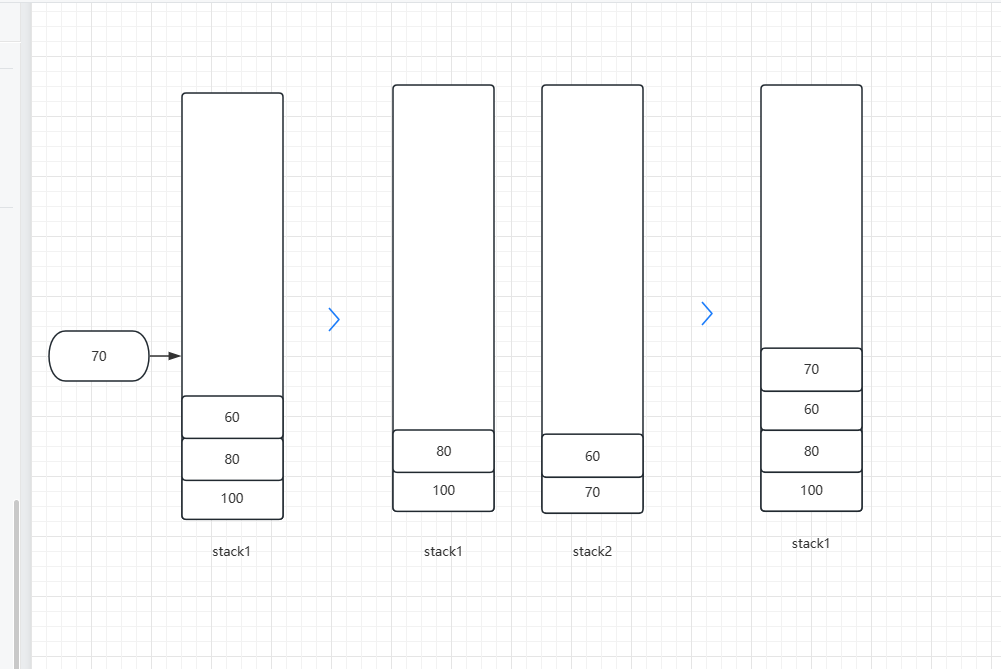
如上图,第一次入栈70这个元素时,比栈顶元素60要大,将price=70入辅助栈,然后遍历主栈栈顶,将小于等于70的元素弹出栈然后push进辅助栈,此时记录辅助栈size为2,然后将辅助栈元素全部弹出并且推入主栈,最后返回size即可。且这样不会修改我主栈元素的原本顺序,就是按照next元素的顺序进行排序的,就也顺便解决了连续这个问题。
同理,后面入75如下图所示:
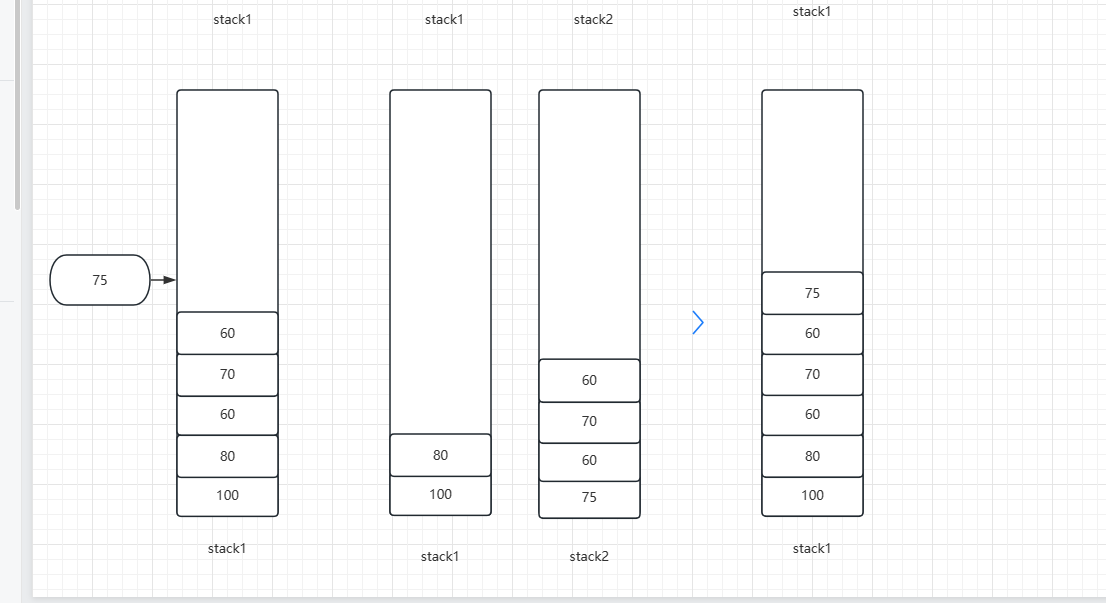
代码如下:
class StockSpanner {private Stack<Integer> stockStack;private Stack<Integer> diffStack;public StockSpanner() {stockStack = new Stack<>();diffStack = new Stack<>();}public int next(int price) {if (stockStack.isEmpty()) {stockStack.push(price);return 1;} else {int diff = price - stockStack.peek();if (diff < 0) {stockStack.push(price);return 1;} else {diffStack.push(price);while (!stockStack.isEmpty() && stockStack.peek() <= price) {diffStack.push(stockStack.pop());}int res = diffStack.size();while (!diffStack.isEmpty()) {stockStack.push(diffStack.pop());}return res;}}}
}
好像这样思路确实没什么问题,运行发现超出时间限制o(╥﹏╥)o:
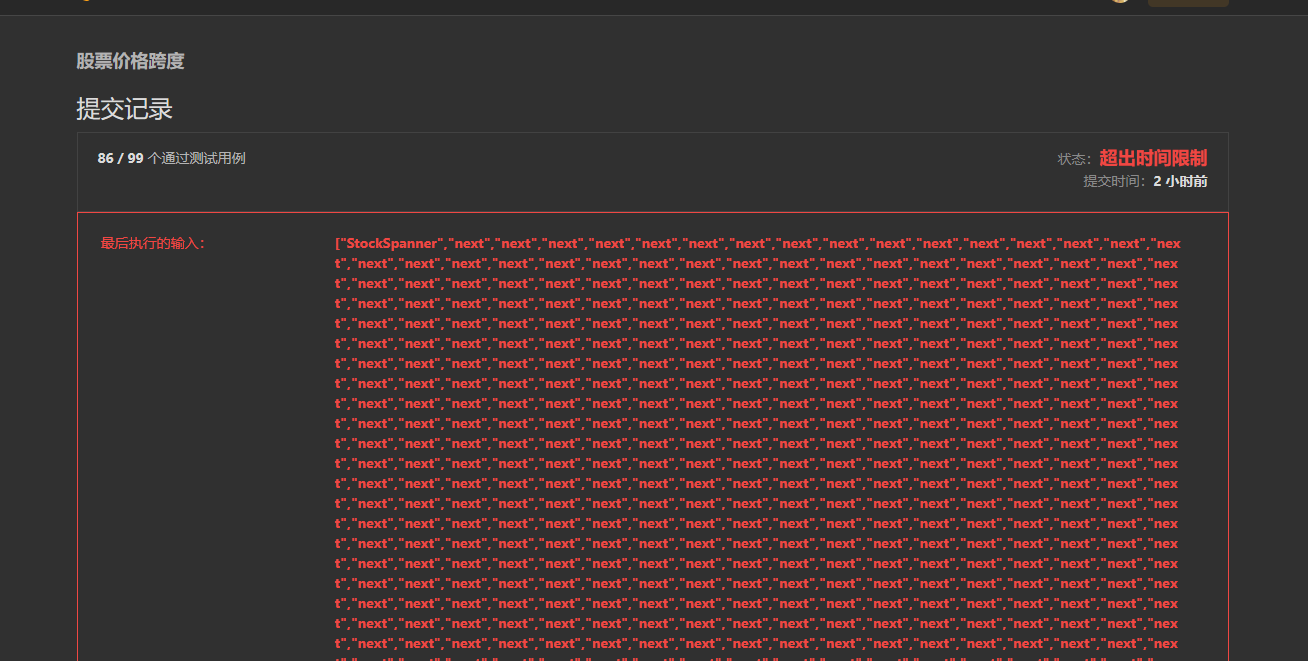
虽说时间复杂度是O(n),可是这样的操作确实还是非常繁琐的,且还需要借助辅助栈且最后主栈的元素量是Next()的调用次数,无效或者其实用不上的元素根本没有pop出栈,导致浪费了很多空间。
所以也就有了后面一种方法–单调栈,该方法不再需要辅助栈,且不会浪费额外空间。
②单调栈
我们将每一个股票价格想象成java的一个对象,它拥有它的id,拥有它的价格,我们可以使用一个int[]去承装他们,int[0]装id,int[1]装价格。
然后我们可以想象下,我们需要比今日股票要小于等于的天数,是否就是将这些对象给按照一个单调递减的顺序排序,如果放入的元素比上一个元素要小,此时结果就是当前放入元素的下标id和上一个元素下标的差值。如果要大,此时不符合单调递减,那么我需要将比它小的元素全部抹去,让我们承装对象的结构始终符合单调递减,此时结果是当前当如元素的下标id和抹去后的它的上一个元素下标id的差值。
为了方便我们后续程序少一些空栈之类的判断,我们初始化的时候可以先push进一个id为0,价格是Integer.MAX的元素,这样到时候我们出栈也不用担心会导致空栈。
而对于next方法,首先是下标,这个很好理解,我们每次调用next方法时,id++即可,很像我们数据库的ID自增策略。由于我们需要的是小于或等于今天价格的最大连续日数,所以是一个单调递减栈,如果要插入的price大于栈顶元素,此时将单调栈的元素依次弹出,并且此时将当前price对应的下标减去出栈后的栈顶元素的下标,这个下标差就是我们需要返回的结果。然后再将当前元素入栈即可然后返回下标差即可。
仍然拿示例1举例:
当我插入100-80-60,由于每次插入都比栈顶元素要小,而当插入70时,此时比栈顶元素60要大,从栈顶开始遍历,一直到栈顶元素大于price为止,此时出栈完后栈顶是id=2,price=80这个元素,然后记录res=4-2=2,然后将price=70,id=4这个元素入栈。
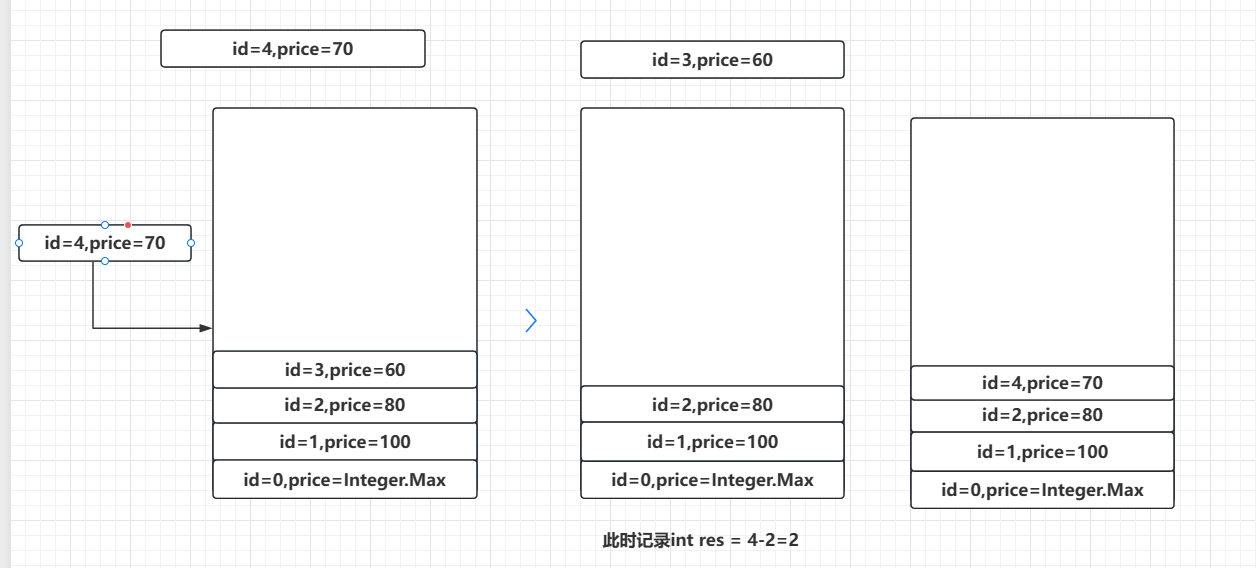
放入60,75同理:
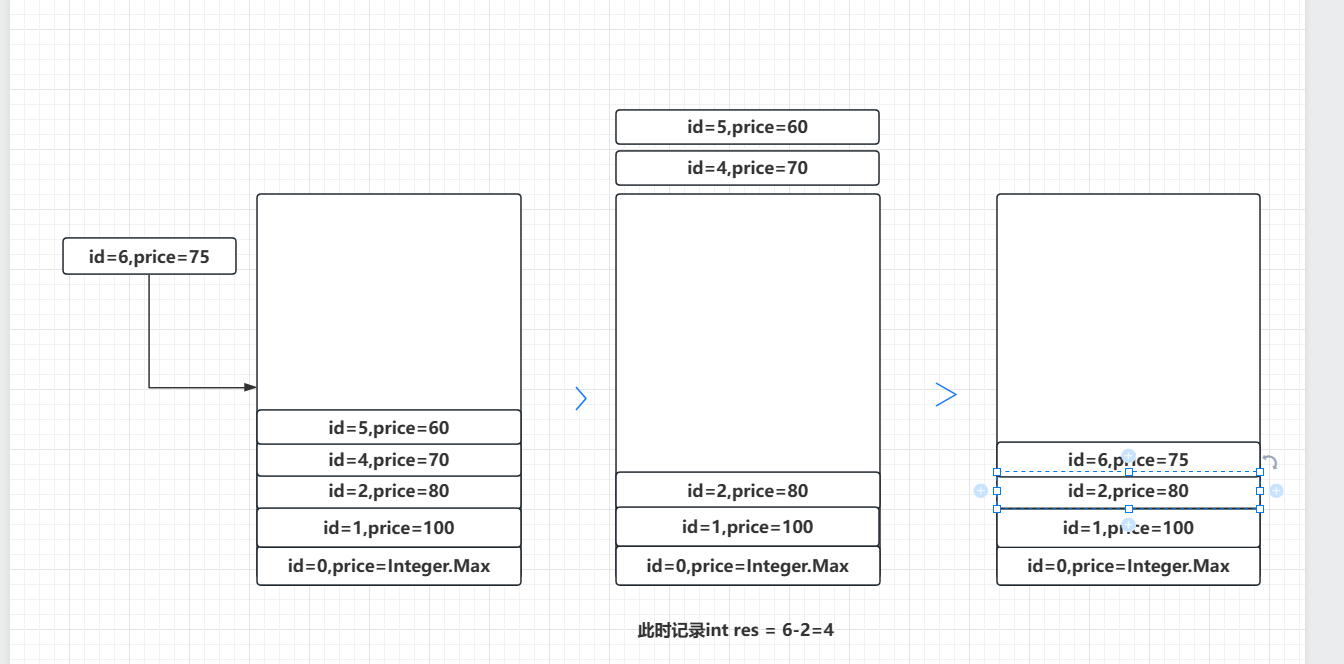
代码如下:
class StockSpanner {private Deque<int[]> stockStack;private int id;public StockSpanner() {stockStack = new ArrayDeque<>();stockStack.push(new int[]{0,Integer.MAX_VALUE});id = 0;}public int next(int price) {id ++;while (price >= stockStack.peek()[1]){stockStack.pop();}int ret = id - stockStack.peek()[0];stockStack.push(new int[]{id, price});return ret;}
}
三、栈排序和单调栈的区别
那么其实栈排序和单调栈是有明显区别的,这里做一个总结:
单调栈:单调栈是一种特殊的栈结构,其插入时保证栈内元素的单调性。通常用于解决数组中下一个更大或下一个更小元素的问题。例如我们可以见我们力扣496下一个更大元素 I这道题,单调栈需要维护一个单调递增或单调递减的栈顶元素序列,每当新元素插入时,都需要判断该元素与栈顶元素的大小关系,不断弹出栈顶元素直到满足单调性。
栈排序:栈排序是对栈内元素进行递增或递减排序的一种思路。通常使用额外的栈来辅助排序。将原始栈的元素依次弹出,插入到辅助栈中的正确位置,最后将辅助栈中的元素重新压回原始栈中,从而实现了栈排序。需要注意的是,仅使用原始栈是无法实现栈排序的,因为栈的弹出顺序一旦改变就无法恢复。
总体来说,单调栈和栈排序都是基于栈实现的常用算法思路,但其应用场景和实现方法不同。单调栈通常用于解决比较问题,需要维护栈内元素的单调性;而栈排序则是对栈内元素的排序,需要额外借助辅助栈实现。
相关文章:

Leetcode901-股票价格跨度
一、前言 本题基于leetcode901股票价格趋势这道题,说一下通过java解决的一些方法。并且解释一下笔者写这道题之前的想法和一些自己遇到的错误。需要注意的是,该题最多调用 next 方法 10^4 次,一般出现该提示说明需要注意时间复杂度。 二、解决思路 ①…...
“传统文化宣传片+虚拟人动捕设备”前景如何?
在数字化时代的发展下,动捕设备的加入,让传播传统文化的虚拟人更具生动表现,拉近人们与传统文化的距离,通过虚拟人动作捕捉动画宣传片,引起更多人对传统文化的关注与传承。 *图片源于网络 深圳文博会创意短片《嗨ICIF…...

节假日moc服务数据:解决用户99%的IT问题
Hi~ 伙伴们,这个国庆假期过得怎么样? 节后第一个工作日如期而至, 忙碌是消除倦怠的最佳良药。 回顾8天假日moc工程师的一组服务数据, 处理事件184起,工单23条。 其中,较为典型案例如下: 1、福建某附属医院…...

WOL唤醒配置(以太网、PHY、MAC)
目录 wol 以太网 MAC PHY RMII 通信配置 总结 wol Wake-on-LAN简称WOL,WOL(网络唤醒) 是一种标准网络协议,它的功效在于让已经进入休眠状态或关机状态的计算机,透过局域网(多半为以太网ÿ…...

MySQL复制,约束条件,查询与安全控制
MySQL之复制 复制表 我有一个表 mysql> show tables; ------------------ | Tables_in_school | ------------------ | student | ------------------mysql> select * from student; -------------------------------------------- | id | name | sec |…...

Java ES 滚动查询
滚动查询(Scroll Query)是 Elasticsearch 提供的一种机制,用于处理大量数据的查询。它允许你在多个请求之间保持“游标”,以便在后续请求中获取更多的结果。 以下是滚动查询的基本工作原理: 1 初始查询: 客户端发送一…...
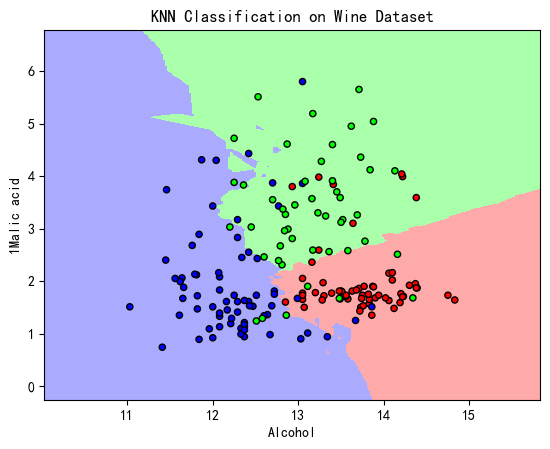
机器学习算法基础--KNN算法分类
文章目录 1.KNN算法原理介绍2.KNN分类决策原则3.KNN度量距离介绍3.1.闵可夫斯基距离3.2.曼哈顿距离3.3.欧式距离 4.KNN分类算法实现5.KNN分类算法效果6.参考文章与致谢 1.KNN算法原理介绍 KNN(K-Nearest Neighbor)工作原理: 在一个存在标签的…...
深入探究 C++ 编程中的资源泄漏问题
目录 1、GDI对象泄漏 1.1、何为GDI资源泄漏? 1.2、使用GDIView工具排查GDI对象泄漏 1.3、有时可能需要结合其他方法去排查 1.4、如何保证没有GDI对象泄漏? 2、进程句柄泄漏 2.1、何为进程句柄泄漏? 2.2、创建线程时的线程句柄泄漏 …...

BLE协议栈1-物理层PHY
从应届生开始做ble开发也差不读四个月的时间了,一直在在做上层的应用,对蓝牙协议栈没有过多的时间去了解,对整体的大方向概念一直是模糊的状态,在开发时也因此遇到了许多问题,趁有空去收集了一下资料来完成了本次专栏&…...
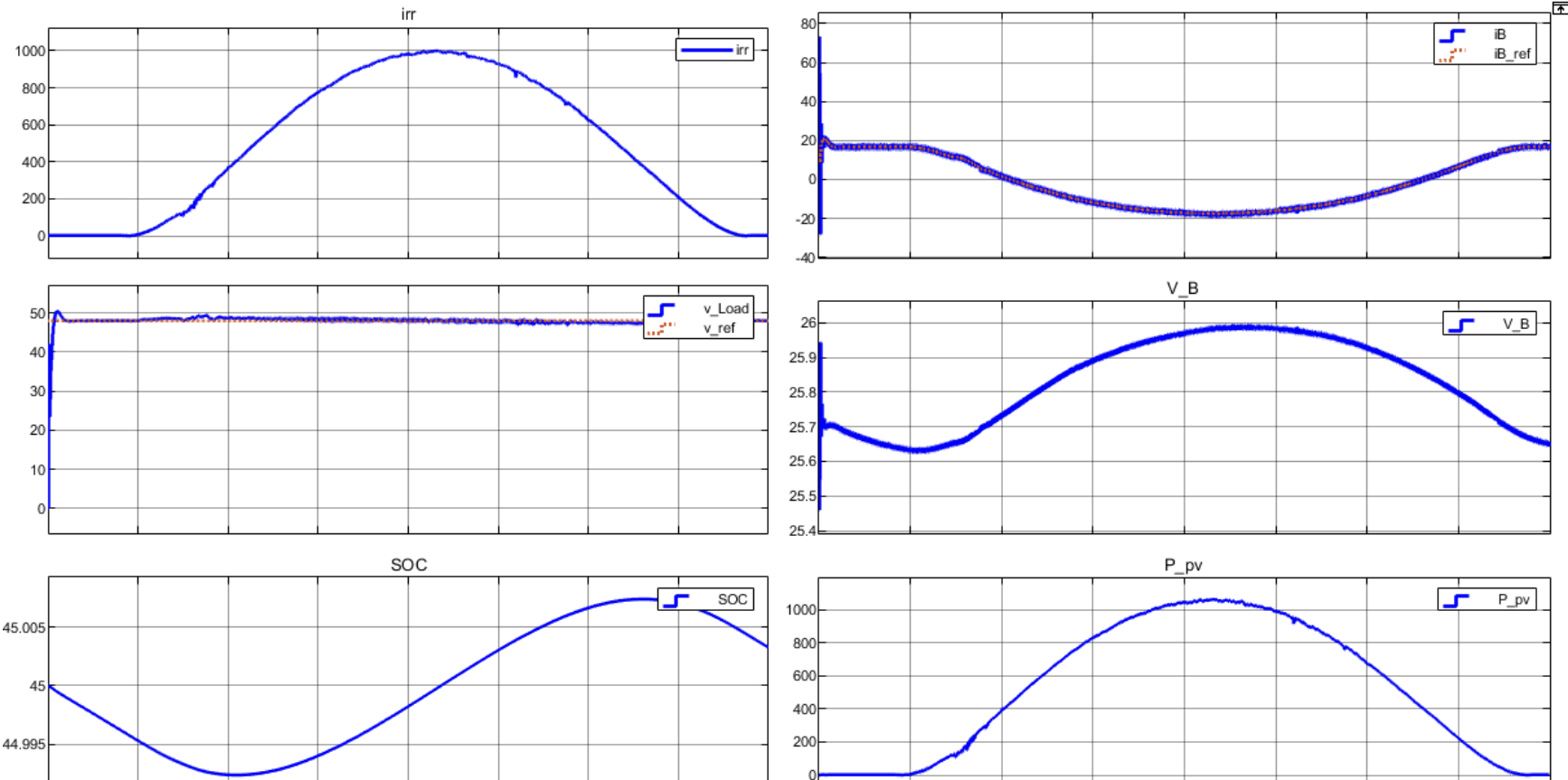
光伏储能直流系统MATLAB仿真(PV光伏阵列+Boost DCDC变换器+负载+双向DCDC变换器+锂离子电池系统)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

C++三大特性——继承(上篇)
文章目录 目录 一、继承的概念及定义 1.1继承的概念 1.2 继承定义 1.2.1定义格式 1.2.2继承关系和访问限定符 1.2.3继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 一、继承的概念及定义 1.1继承的概念 继承(inherita…...

docker系列(9) - docker-compose
文章目录 9. compose编排9.1 介绍9.2 安装9.3 compose常用命令9.4 实战Springboot部署9.4.1 准备组件配置文件9.4.1.1 redis的配置文件9.4.1.2 MySQL的配置文件9.4.1.3 SpringBoot打包文件 9.4.2 准备docker-compose.yml9.4.3 启动服务9.4.4 测试验证 9.5 实战ElasticsearchKib…...

Vue中如何进行日历展示与操作
在Vue中创建交互式日历应用 在Web开发中,创建一个交互式的日历应用是一项常见的任务。Vue.js作为一个流行的JavaScript框架,提供了许多便捷的工具和组件来简化日历的开发。本文将介绍如何使用Vue来创建一个简单但功能强大的日历应用,包括展示…...

SpringBoot 返回图片、Excel、音视频等流数据几种处理方式
方式一:直接针对响应对象(response)实现 @RestController @Slf4j @Api(tags = SwaggerConfig.TAG_IMAGE) @RequestMapping(SwaggerConfig.TAG_IMAGE) public class ImageController {@GetMapping(value = "/getImage")@ApiOperation("获取图片-以ImageIO流形…...
【Vue面试题一】、说说你对 Vue 的理解
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:有使用过vue吗ÿ…...

vue3 axios
npm install axios import axios from axios // 创建axios实例 const request axios.create({baseURL: ,// 所有的请求地址前缀部分(没有后端请求不用写)timeout: 80000, // 请求超时时间(毫秒)withCredentials: true,// 异步请求携带cookie// headers: {// 设置后端需要的传…...

划片机:半导体生产的必备设备
划片机是半导体加工行业中的重要设备,主要用于将晶圆切割成晶片颗粒,为后道工序粘片做好准备。随着国内半导体生产能力的提高,划片机市场的需求也在逐渐增加。 在市场定位上,划片机可以应用于半导体芯片和其他微电子器件的制造过程…...

电路维修——双端队列BFS
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。 翰翰的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障,导致无法启动。电路板的整体结构是一个 R 行 C 列的网格&#…...
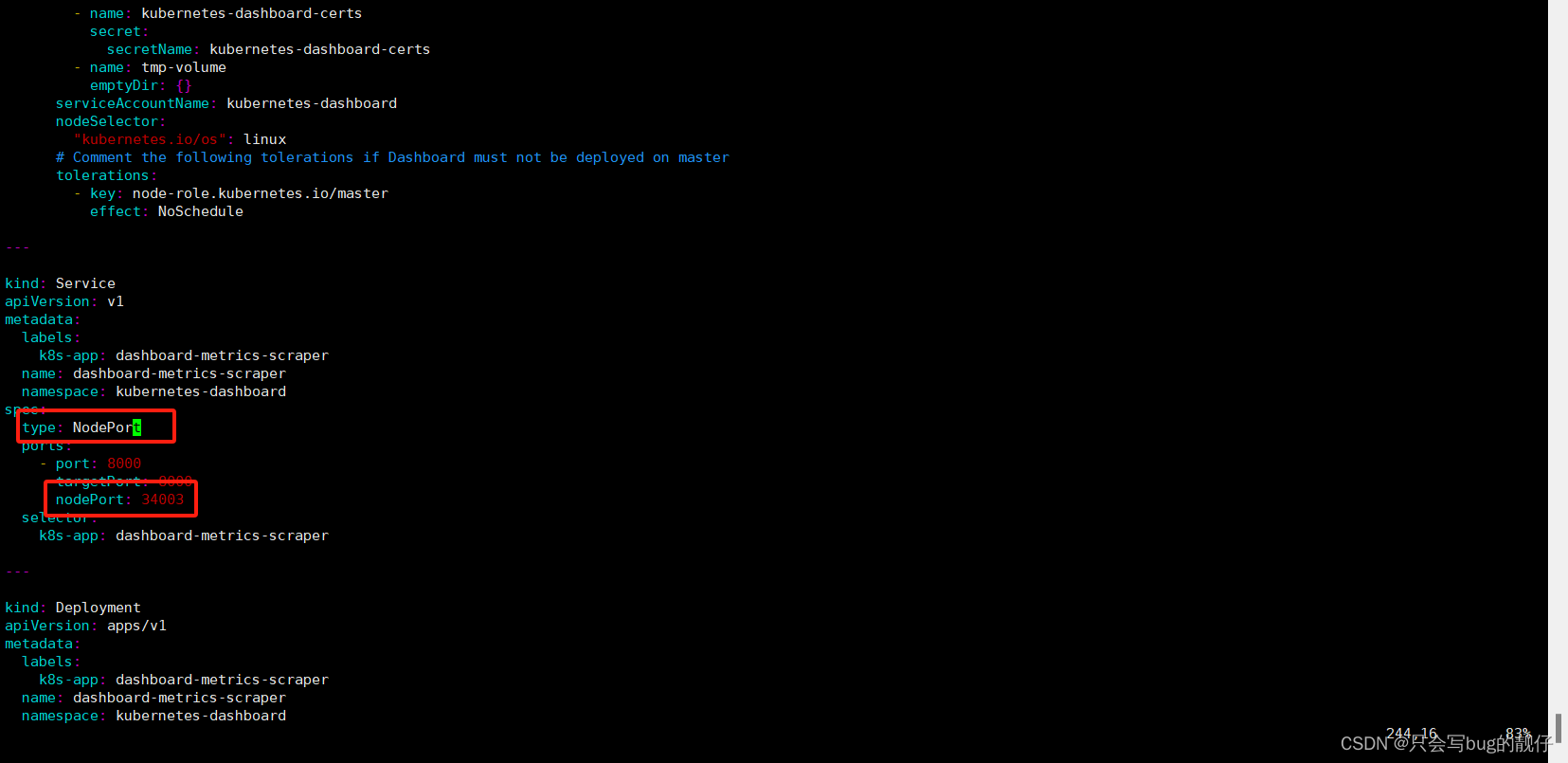
乌班图22.04 kubeadm简单搭建k8s集群
1. 我遇到的问题 任何部署类问题实际上对于萌新来说都不算简单,因为没有经验,这里我简单将部署的步骤和想法给大家讲述一下 2. 简单安装步骤 准备 3台标准安装的乌班图server22.04(采用vm虚拟机安装,ip为192.168.50.3࿰…...
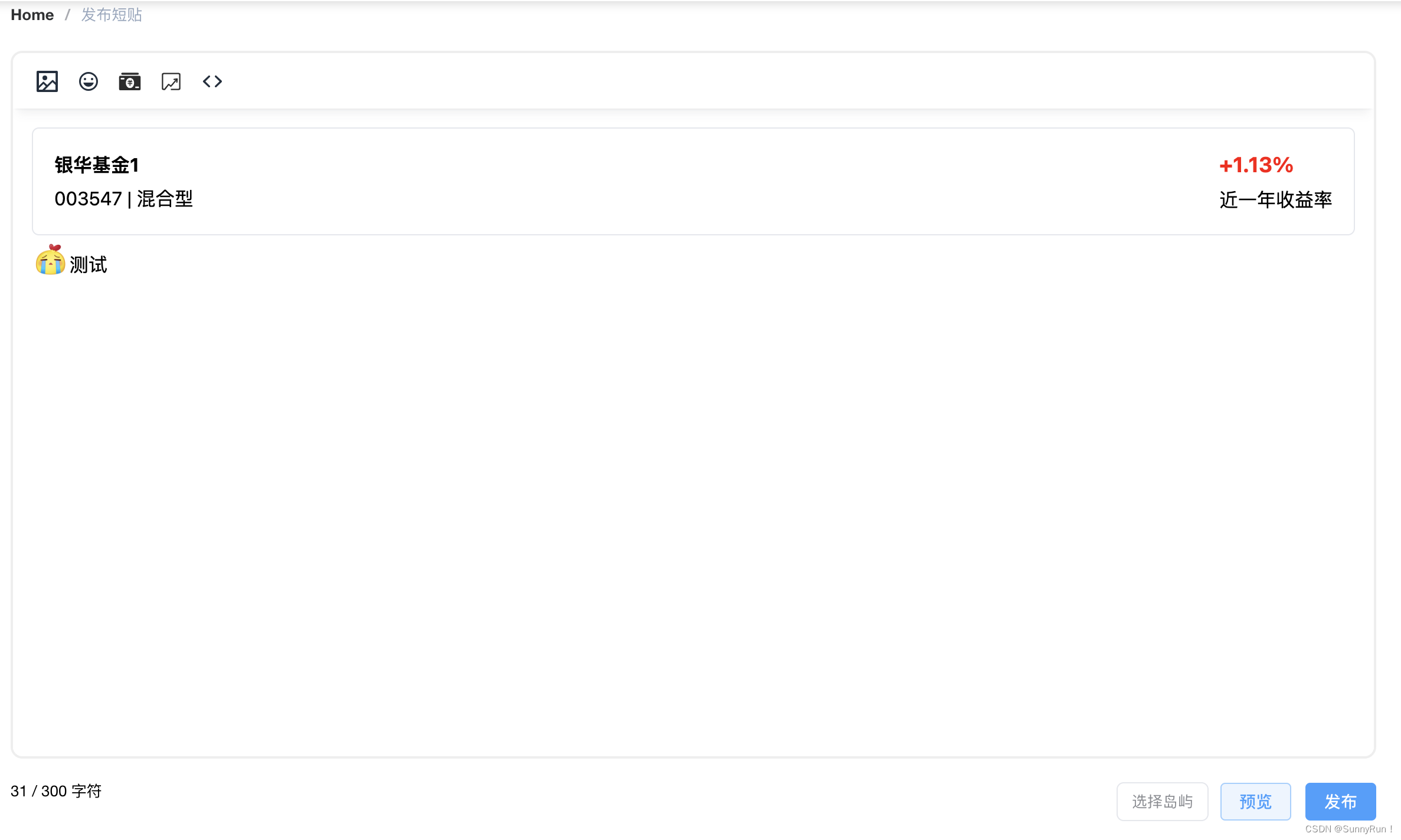
vue3富文本编辑器的二次封装开发-Tinymce
欢迎点击领取 -《前端面试题进阶指南》:前端登顶之巅-最全面的前端知识点梳理总结 *分享一个使用比较久的🪜 简介 1、安装:pnpm add tinymce / pnpm add tinymce/tinymce-vue > Vue3 tinymce tinymce/tinymce-vue 2、功能实现图片上传…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
