数据结构基本概念-Java常用算法
数据结构基本概念-Java常用算法
- 1、数据结构基本概念
- 2、数据逻辑结构
- 3、算法时间复杂度
1、数据结构基本概念
- 数据(Data):数据是信息的载体,其能够被计算机识别、存储和加工处理,是计算机程序加工的“原材料”。
- 数据元素(Data Element):数据元素是数据的基本单位,其也称元素、结点、顶点、记录等。一般来说,一个数据元素可以由若干个数据组成,数据项是具有独立含义的最小标识单位。数据项也可称为字段、域、属性等。
- 数据结构(Data Structure):数据结构指的是数据之间的相互关系,也就是数据的组织形式。
数据结构的内容:
- 数据的逻辑结构: 线性结构、树型结构、图结构
- 数据的存储结构: 顺序存储、链式存储
- 数据操作: 也就是数据的运算,基于数据的逻辑结构上,最常用的运算包括检索、插入、删除、更新、排序等。
数据类型:通常是指高级程序设计语言支持的基本数据类型,如C/C++、Java、Python、Kotlin等。
抽象数据类型:数据的组织,及其相关的操作。
2、数据逻辑结构
线性结构: 除第一个和最后一个数据元素外,每个数据只有一个唯一的前驱数据元素和一个唯一个的后驱数据元素。
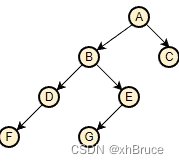
树型结构: 除根节点外,每个数据元素只有一个唯一的前驱数据元素,可有零个或若干个后驱数据元素。
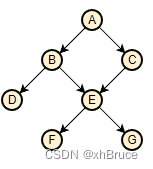
图型结构: 每个数据元素可有零个或若干个前驱数据元素和零个或若干个后驱数据元素。
3、算法时间复杂度
算法时间复杂度:算法的耗时与算法所处理的数据个数 n 的函数关系的分析;主要分析算法的耗时与算法处理数据个数 n 的 数量级 意义上的函数关系。
算法的时间复杂度与空间复杂度通常是矛盾的。目前计算机内存下降趋势下,当发生矛盾时,对于大多数情况来说,算法的时间复杂度应首先被考虑。
【定义】 T ( x ) = O ( f ( n ) ) T(x) = O(f(n)) T(x)=O(f(n))当且仅当存在正常数 c c c和 n 0 n_{0} n0,对所有的 n ( n ≥ n 0 ) n(n\ge n_{0} ) n(n≥n0)满足 T ( n ) ≤ c f ( n ) T(n)\le cf(n) T(n)≤cf(n)。
当算法的时间复杂度 T ( n ) T(n) T(n)和数据个数 n n n无关系时, T ( n ) ≤ c × 1 T(n) \le c\times 1 T(n)≤c×1,所以此时算法的时间复杂度 T ( n ) = O ( 1 ) T(n) = O(1) T(n)=O(1);
当算法的时间复杂度 T ( n ) T(n) T(n)和数据个数 n n n为线性关系时, T ( n ) ≤ c n T(n)\le cn T(n)≤cn,所以此时算法的时间复杂度 T ( n ) = O ( n ) T(n) = O(n) T(n)=O(n);
当算法的时间复杂度 T ( n ) T(n) T(n)和数据个数 n n n为平方关系时, T ( n ) ≤ c n 2 T(n)\le cn^2 T(n)≤cn2,所以此时算法的时间复杂度 T ( n ) = O ( n 2 ) T(n) = O(n^2) T(n)=O(n2);
依次类推,还有 O ( n 3 ) O(n^3) O(n3)、 O ( log 2 n ) O(\log_{2}{n}) O(log2n)、 O ( lg n ) O(\lg_{}{n}) O(lgn)、 O ( lg n ) O(\lg_{}{n}) O(lgn)、 O ( 2 n ) O(2^n) O(2n)等
算法的时间复杂度是衡量一个算法好坏的重要指标。一般来说,具有多项式时间复杂度(如 O ( n ) O(n) O(n)、 O ( n 2 ) O(n^2) O(n2)、 O ( n 6 ) O(n^6) O(n6)等)的算法,是可以接收的、可实际使用的算法;而具有指数时间复杂度(如 O ( 2 n ) O(2^n) O(2n)、 O ( n n ) O(n^n) O(nn)、 O ( n ! ) O(n!) O(n!)等)的算法,是理论上可以计算,但实际上不可计算的问题,通常称作难解的问题。
i i i n n n n 2 n^2 n2 n 3 n^3 n3 2 n 2^n 2n n ! n! n! n n n^n nn 1 1 1 1 2 1 1 2 2 4 8 4 2 4 3 3 9 27 8 6 27 … … … … … … … 10 10 100 1000 1024 3628800 1.9 × 1 0 10 1.9\times 10^{10} 1.9×1010 … … … … … … … 20 20 400 8000 1048376 2.4 × 1 0 18 2.4\times 10^{18} 2.4×1018 1.0 × 1 0 25 1.0\times 10^{25} 1.0×1025 … … … … … … … 100 100 10000 1.0 × 1 0 6 1.0\times 10^{6} 1.0×106 1.3 × 1 0 30 1.3\times 10^{30} 1.3×1030 9.3 × 1 0 157 9.3\times 10^{157} 9.3×10157 1.0 × 1 0 200 1.0\times 10^{200} 1.0×10200 通常当基本语句计算次数超过 1.0 × 1 0 15 1.0\times 10^{15} 1.0×1015次时,该算法的计算机执行时间就比较长。设 计算机每秒可执行1亿次( 1.0 × 1 0 9 1.0\times 10^{9} 1.0×109)条基本语句 ,则执行一个需要 1.0 × 1 0 15 1.0\times 10^{15} 1.0×1015次基本操作的算法时间为:
T = ( 1.0 × 10 15 ) / ( 1.0 × 10 9 ) = 1.0 × 10 6 ( 秒 ) T = (1.0\times {10}^{15}) / (1.0\times {10}^{9}) = 1.0\times {10}^{6}(秒) T=(1.0×1015)/(1.0×109)=1.0×106(秒)
= ( 1.0 × 10 6 ) / 3600 = 277.8 ( 天 ) = (1.0\times {10}^{6}) / 3600 = 277.8(天) =(1.0×106)/3600=277.8(天)
= 277.8 / 24 = 11.6 ( 天 ) = 277.8 / 24 = 11.6(天) =277.8/24=11.6(天)
相关文章:
数据结构基本概念-Java常用算法
数据结构基本概念-Java常用算法 1、数据结构基本概念2、数据逻辑结构3、算法时间复杂度 1、数据结构基本概念 数据(Data):数据是信息的载体,其能够被计算机识别、存储和加工处理,是计算机程序加工的“原材料”。数据元…...

流程图设计制作都有哪些好用的工具
流程图是一种直观的图形表示方式,通常用于显示事物的过程、步骤和关系。在现代工作中,设计师经常需要绘制各种流程图来解释工作过程、产品设计等。本文将为您推荐7个流程图软件,以帮助您快速绘制高效的流程图,并提高工作效率。 即…...

2023-10-7
今日感冒了,整个人都不舒服,现在才 8 点,已经不想学习了。嗓子眼感觉不属于我了,痛死了。然后头也晕。 哎,今天又啥也没干 今日学习: 哎,今天就做了 RWCTF2022-Digging-into-kernel-2 这道题…...
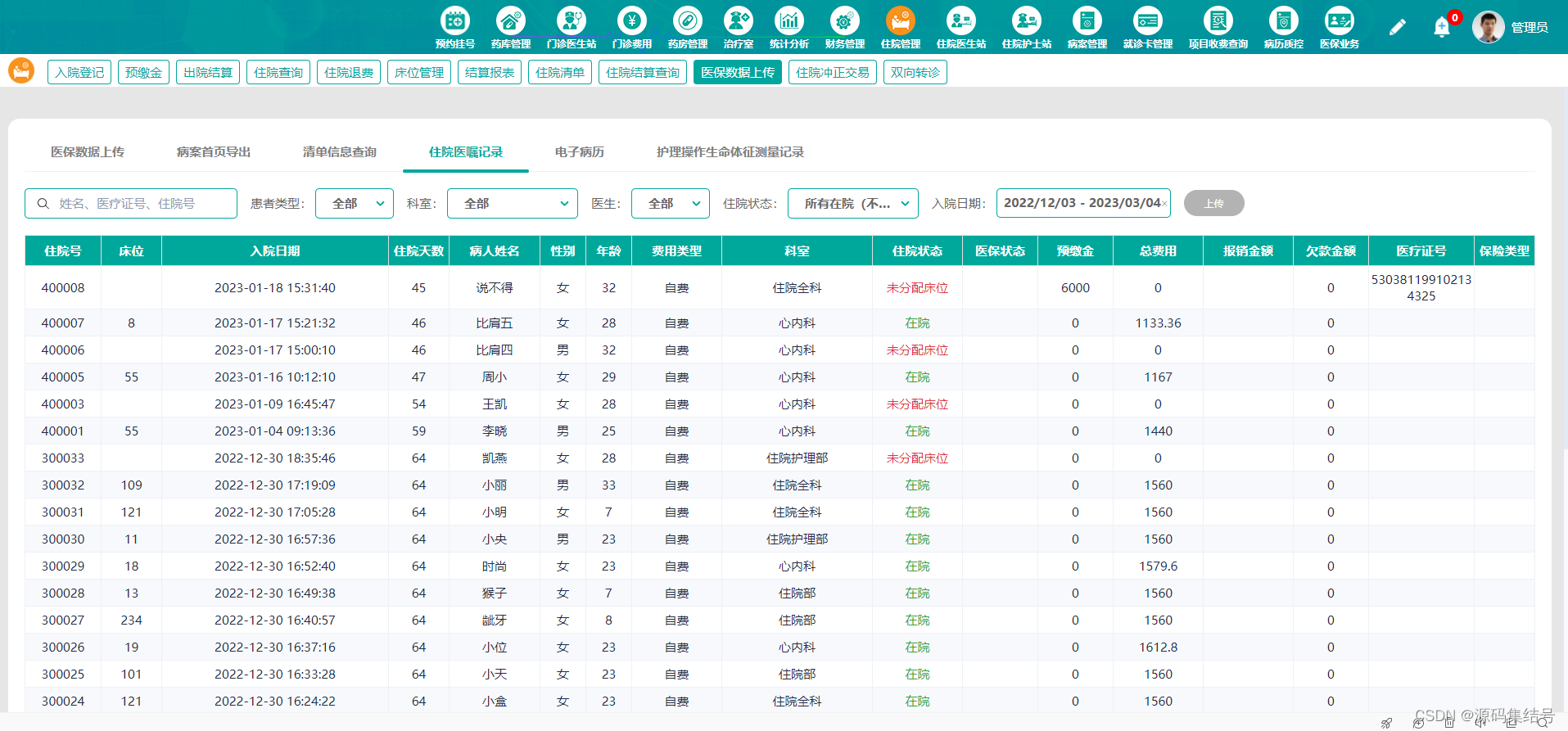
【java源码】二甲医院his系统全套源码 云HIS系统源码
基层医院云HIS系统源码 一款满足基层医院各类业务需要的云HIS系统。该系统能帮助基层医院完成日常各类业务,提供病患挂号支持、病患问诊、电子病历、开药发药、会员管理、统计查询、医生站和护士站等一系列常规功能,还能与公卫、PACS等各类外部系统融合&…...

LRU 缓存 -- 哈希链表
相关题目 146. LRU 缓存 要让 put 和 get ⽅法的时间复杂度为 O(1),我们可以总结出 cache 这个数据结构必要的条件: 1、显然 cache 中的元素必须有时序,以区分最近使⽤的和久未使⽤的数据,当容量满了之后要删除最久未使⽤的那个元…...

DWC数字世界大会先导论坛将于10月13日在宁波举办 | 数字技术赋能世界可持续发展
农业经济影响世界数千年,工业经济从欧美发源开始已有数百年,数字经济作为世界未来发展之大势,将成为影响未来数百年的世界命题。在以中国式现代化全面推进中华民族伟大复兴的历史征程中,数字技术、数字经济作为中国式现代化实践最…...

Springboot实现登录功能(token、redis、登录拦截器、全局异常处理)
登录流程: 1、前端调用登录接口,往接口里传入账号,密码 2、根据账号判断是否有这个用户,如果有则继续判断密码是否正确 3、验证成功后,则是根据账号,登录时间生成token(用JWT) 4、将…...

AI工程化—— 如何让AI在企业多快好省的落地?
文章目录 前言内容简介读者对象专家推荐目录赠书活动 前言 作为计算机科学的一个重要领域,机器学习也是目前人工智能领域非常活跃的分支之一。机器学习通过分析海量数据、总结规律,帮助人们解决众多实际问题。随着机器学习技术的发展,越来越多…...

mysqld_multi测试
mysqld_multi测试 mysql版本:5.7.25-log 在OS上分别安装了两套mysql, data目录为/mysql/mysql3306、 /mysql/mysql3307 。 端口分别为3306 、3307 配置文件为: /mysql/mysql3306/my.cnf /mysql/mysql3307/my.cnf 参考文档: htt…...

MDC方式实现简单链路追踪
MDC 方式实现日志链路追踪 拦截器 package com.cdn.log.interceptor;import com.cdn.log.consts.CLogConst; import com.cdn.log.utils.IdUtil; import org.slf4j.MDC; import org.springframework.util.StringUtils; import org.springframework.web.servlet.ModelAndView; im…...

Linux深度学习:除基本命令操作外的实用操作
Linux深度学习:除基本命令操作外的实用操作 软件安装systemctl软连接日期、时区IP地址、主机名网络传输下载和网络请求端口 进程管理主机状态系统资源监控磁盘信息监控网络状态监控 环境变量上传、下载压缩、解压root用户、用户、用户组管理查看、修改权限控制 软件…...

app对接广告变现平台:影响app广告单价的4大因素
在移动应用开发者和媒体公司竞相寻求提高广告变现效率的今天,理解影响APP广告单价的关键因素至关重要。广告单价是广告收入的核心组成部分,它受多种因素的影响,直接关系到媒体的盈利能力。主要因素大概有以下几点:#APP广告变现# …...
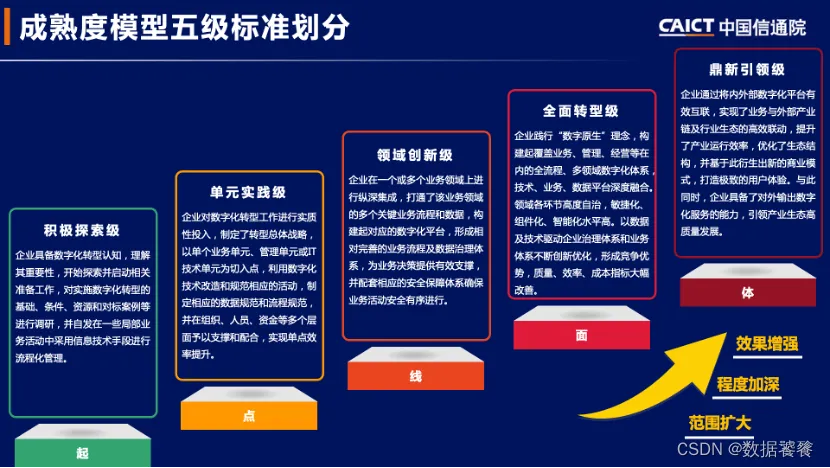
【数字化转型】10大数字化转型能力成熟度模型01(IOMM)
一、前言 数字化转型是数据化能力建设的目标和价值,作为一个新兴的课题,目前为止并未出现一个统一的数字化转型成熟度模型。不同的企业和机构,根据自身的发展和认知,推出了自己的企业级或者准行业级标准。这些标准具有很强的参考意…...

2023腾讯云轻量应用服务器和普通服务器有什么区别?
腾讯云轻量服务器和云服务器有什么区别?为什么轻量应用服务器价格便宜?是因为轻量服务器CPU内存性能比云服务器CVM性能差吗?轻量应用服务器适合中小企业或个人开发者搭建企业官网、博客论坛、微信小程序或开发测试环境,云服务器CV…...

SSL证书是什么?1分钟get
在当今互联网世界中,保护数据的完整性和隐私性至关重要,由此,在网络数据安全保护领域,作为保护网络传输数据安全的SSL证书越来越频繁出现。那么你知道SSL证书是什么?SSL证书有哪些类型?SSL证书有什么用吗&a…...

3D打印机升级killpper
本来是想整台新机的,但是想想老机器4max也不能就此放弃,看了看视频,改装升级似乎也没有那么难。然后就是换了喷头、皮带、轴承、挤出机、打印平台、加热板等等。做了干燥箱,改装挤出机结构来适配,风扇口也一并搞掉&…...
源码编译dotnetcore的runtime
为了dotnetcore运行时的安可目标,特意在国庆假期研究了怎么编译dotnetcore的runtime。由于我们用的是.net6,最新的是8,所以从github下载的.net6的分支代码进行的编译。查遍了国内外资料,估计微软服务太体贴了,竟然没什…...

11个在线免费调整图像大小而不会降低质量工具
图片对于增强您的网站、博客和其他在线平台的视觉效果非常重要,而这些图片的正确尺寸在这里起着重要作用。如果您有多种尺寸的图像并且想要调整为一个尺寸,可以使用多种在线图像调整工具。使用在线工具,没有软件下载或安装的麻烦,…...
聊聊机器的情感和意识
这是鼎叔的第七十七篇原创文章。行业大牛和刚毕业的小白,都可以进来聊聊。 欢迎关注本公众号《敏捷测试转型》,星标收藏,大量原创思考文章陆续推出。 鼎叔的个人专著《无测试组织-测试团队的敏捷转型》无测试组织:测试团队的敏捷…...
)
职责链模式,非常容易被忽视的设计模式之一(设计模式与开发实践 P13)
文章目录 现实实例反例优化异步职责链 职责链模式在 C# 中是常见的,他的定义是:使多个对象都有机会处理请求,从而避免发送者和请求者之间的耦合关系,将对象连成一条链并传递该请求,直到有一个对象处理它为止 现实实例…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

信息收集:从图像元数据(隐藏信息收集)到用户身份的揭秘 --- 7000
目录 🌐 访问Web服务 💻 分析源代码 ⬇️ 下载图片并保留元数据 🔍 提取元数据(重点) 👤 生成用户名列表 🛠️ 技术原理 图片元数据(EXIF 数据) Username-Anarch…...