010:连续跌3天,同时这三天收盘价都在20日均线下,第四天上涨的概率--以京泉华为例
对于《连续跌三天,压第四天上涨的盈利计算》,我们可以继续优化这个策略,增加条件:同时三天都收盘在20日均线下。
因为我们上一篇《获取20日均线数据到excel表中》获得了20日均线数据,我们可以利用均线数据来编写新的脚本。这里我们用$京泉华(SZ002885)$为例子。
步骤:
1,用《根据股票代码和起始日期获取K线数据到excel表》的脚本获取京泉华最近大约三年的K线数据,得到文件《002885.csv》
2,用《获取20日均线数据到excel表中》的脚本获取到文件《avg_20_002885.csv》
3,最后用以下脚本(名为:three_day_green_20_low.py)来获取最终的结果:
import tkinter as tk
from tkinter import filedialog
import pandas as pdpath=''
benjin = 10000.00def open_file():global pathpath = filedialog.askopenfilename(initialdir="./", title="Select file", filetypes=(("Text files", "*"), ("All files", "*.*")))print("Selected file:", path)root.quit() # 选择完文件后退出主循环root = tk.Tk()
root.title("File Selector")button = tk.Button(root, text="Open File", command=open_file)
button.pack()root.mainloop()# 读取表格数据
data = pd.read_csv(path, delimiter=',')# 初始化计数器
total_count = 0
old_count = 0
up_count = 0
sum = 0# 遍历数据
for i in range(len(data)-3):if(i<20):continue# 判断是否连续三天下跌if data['涨跌幅'][i] < 0 and data['涨跌幅'][i+1] < 0 and data['涨跌幅'][i+2] < 0:old_count += 1if data['收盘'][i] < data["20日均线"][i] and data['收盘'][i+1] < data["20日均线"][i+1] and data['收盘'][i+2] < data["20日均线"][i+2] :total_count += 1if(i+4<len(data)):sum = data['涨跌幅'][i+4]/100*benjin + sum# 判断第四天是否上涨if data['涨跌幅'][i+3] > 0:up_count += 1# 计算概率
probability = up_count / total_count
print("K线总数:",len(data))
print("连续三天下跌的次数为:", old_count)
print("连续三天下跌,而且三天收盘价都小于20日均线的次数:", total_count)print("连续三天下跌后,而且三天收盘价都小于20日均线,下一天上涨次数为:", up_count)
print("连续三天下跌后,而且三天收盘价都小于20日均线,下一天上涨的概率为:", probability)
print("出现连续三天下跌,而且三天收盘价都小于20日均线,平均需要多少条K线:" , len(data)/total_count)
print("假如每次买",benjin,"最后会赚的钱为:",sum)执行后,选择文《avg_20_002885.csv》:
打开,然后看结果:
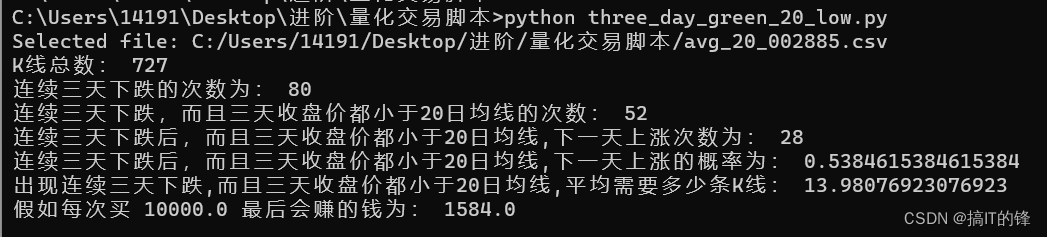
可以多统计不同的个股,找到一些相对合适的标的。
相关文章:

010:连续跌3天,同时这三天收盘价都在20日均线下,第四天上涨的概率--以京泉华为例
对于《连续跌三天,压第四天上涨的盈利计算》,我们可以继续优化这个策略,增加条件:同时三天都收盘在20日均线下。 因为我们上一篇《获取20日均线数据到excel表中》获得了20日均线数据,我们可以利用均线数据来编写新的脚…...

MATLAB与Python:优势与挑战
本文旨在探讨MATLAB与Python在特定领域内的使用情况,并分析两者之间的优势和挑战。 MATLAB和Python都是流行的编程语言,广泛应用于科学计算、数据分析和机器学习等领域。在某些领域,如航空航天工程、自动化和电子工程嵌入式系统开发等&#…...
CSP-J第二轮试题-2019年-1、2题
文章目录 参考:总结 [CSP-J2019] 数字游戏题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示答案答案2 [CSP-J 2019] 公交换乘题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示…...
深入理解 python 虚拟机:原来虚拟机是这么实现闭包的
深入理解 python 虚拟机:原来虚拟机是这么实现闭包的 在本篇文章当中主要从虚拟机层面讨论函数闭包是如何实现的,当能够从设计者的层面去理解闭包就再也不用死记硬背一些闭包的概念了,因为如果你理解闭包的设计原理之后,这些都是…...
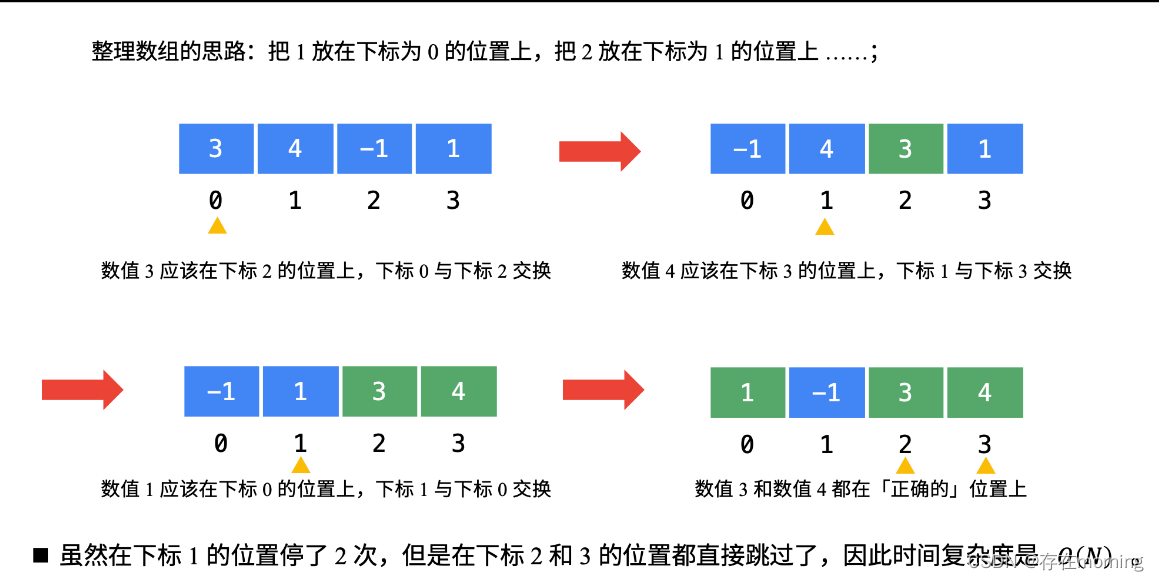
【数据结构-哈希表 一】【原地哈希】:缺失的第一个正整数
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【原地哈希】,使用【数组】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...
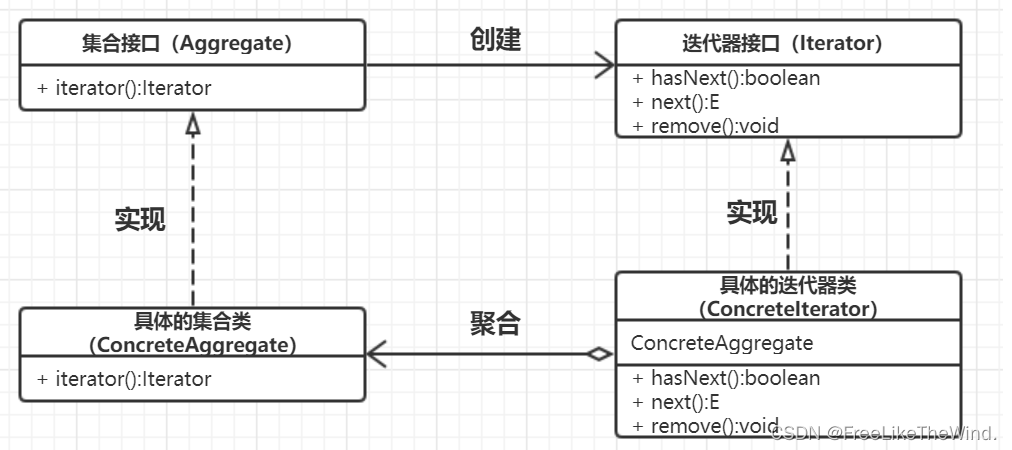
【C++设计模式之迭代器模式】分析及示例
简介 迭代器模式是一种行为型设计模式,它提供了一种顺序访问聚合对象元素的方法,而又不需要暴露聚合对象的内部结构。迭代器模式通过将遍历算法封装在迭代器对象中,可以使得遍历过程更简洁、灵活,并且符合开闭原则。 描述 迭代…...

【代码随想录】LC 27. 移除元素
文章目录 前言一、题目1、原题链接2、题目描述 二、解题报告1、思路分析2、时间复杂度3、代码详解 三、知识风暴 前言 本专栏文章为《代码随想录》书籍的刷题题解以及读书笔记,如有侵权,立即删除。 一、题目 1、原题链接 27. 移除元素 2、题目描述 二、…...
)
crash工具分析dma设备内存踩踏(一)
背景介绍 我们的客户在利用我们提供的SDK参考方案开发相关产品时,在产品方案上进行一些基础老化测试时,极低概率出现kernel随机panic问题,由于场景复杂,无法单独针对特定模块或功能进行拆解来进行实验排查,只能基于已…...
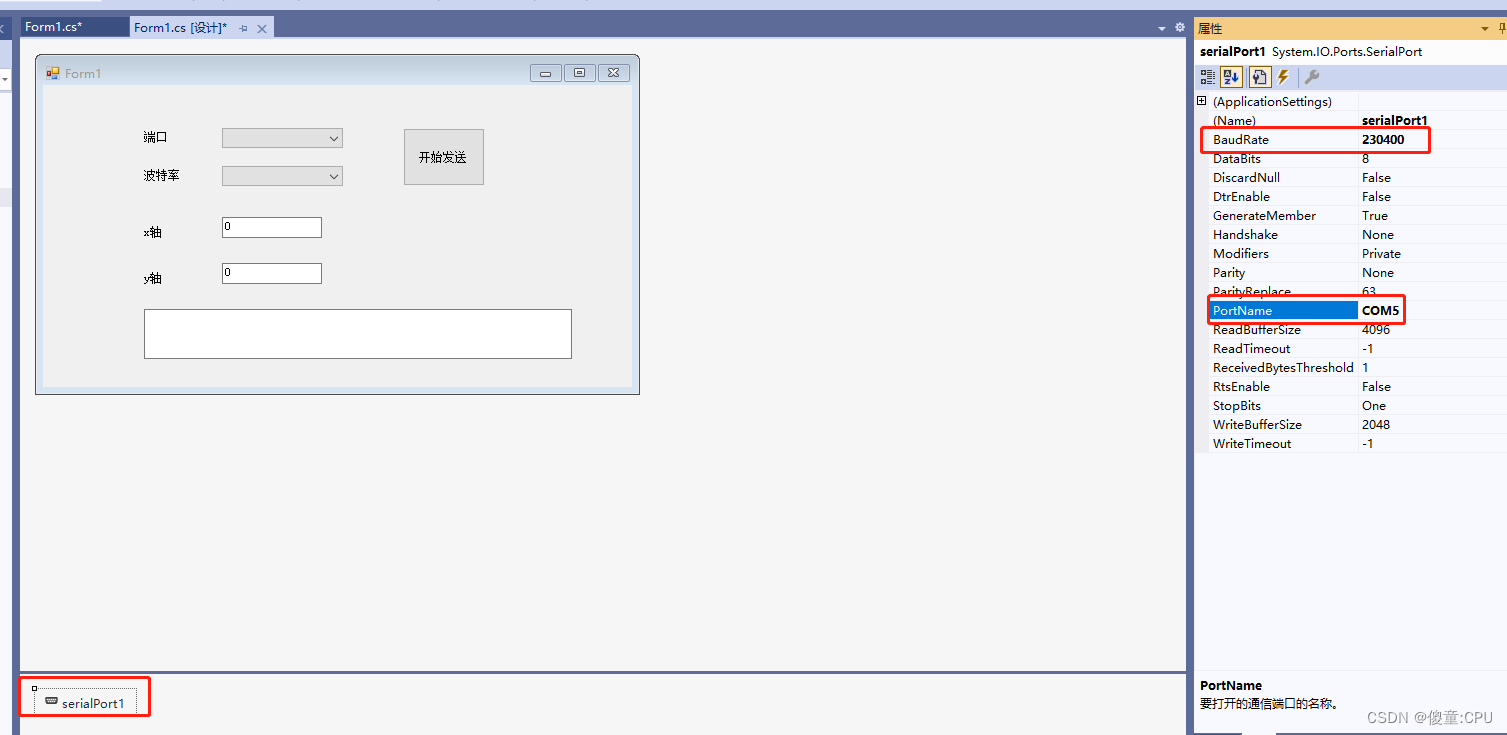
C#上位机——根据命令发送
C#上位机——根据命令发送 第一步:设置窗口的布局 第二步:设置各个属性 第三步:编写各个模块之间的关系...

BEVFormer代码跑通
1 环境配置 1.1 环境安装 # 1 拉取源码 github加速代理https://ghproxy.com/ git clone https://github.com/fundamentalvision/BEVFormer.git# 2 创建虚拟环境 conda create -n bev python3.8 -y# 3 激活虚拟环境 conda activate bev# 4.1 安装torch,torchvision,torchaud…...
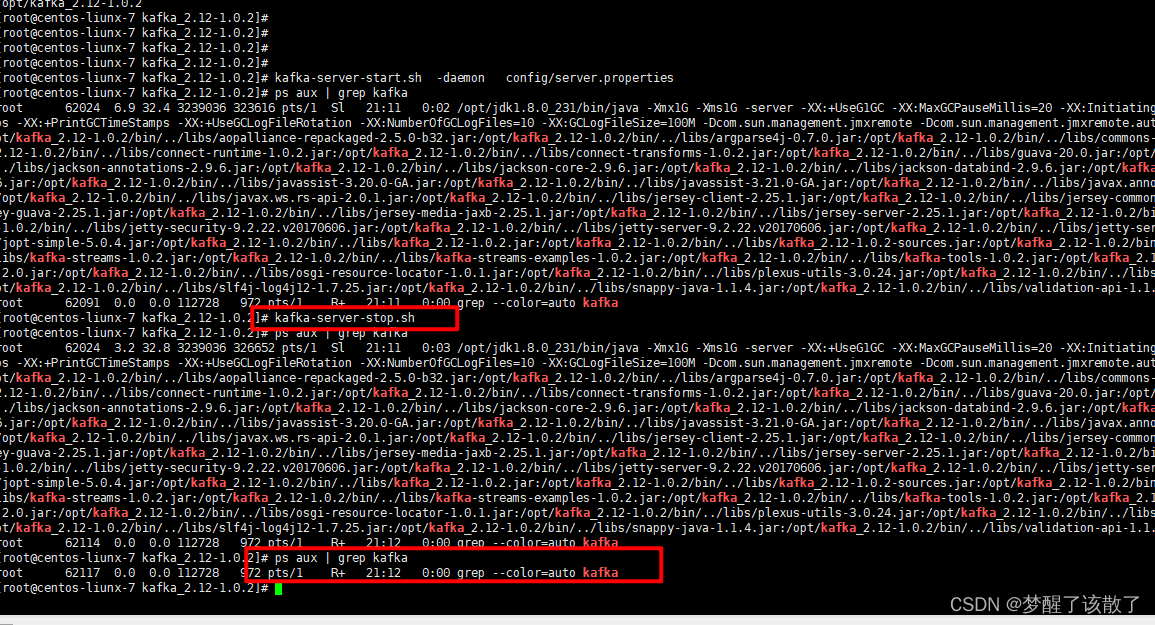
kafka安装
kafka安装 1 kafka概念 1.1 kafka介绍 kafka是最初有Linkedin公司开发的,是一个分布式,分区,多副本,多生产者,多订阅者,基于zookeeper协调的分布式日志系统。具有高吞吐量,可扩展性和可容错性…...

Mac上安装Java的JDK多版本管理软件jEnv
JDK的多版本管理软件主要有以下三种: jEnv jEnv 是一个命令行工具,可以帮助您管理和切换不同版本的 Java 环境。它可以让您在不同的项目之间轻松切换 Java 版本。您可以使用 jenv global 命令设置全局 Java 版本,也可以使用 jenv local 命令…...

linux常见命令以及jdk,tomcat环境搭建
目录 Is pwd cd touch cat echo vim 复制粘贴 mkdir rm cp jdk部署 1. yum list | grep jdk进行查找编辑 2.安装编辑 3.再次确认 4.判断是否安装成功 tomcat安装 1.下载压缩包,把压缩包上传至linux(可能需要yum install lrzsz) 2.解压缩unzip 压缩包名&…...
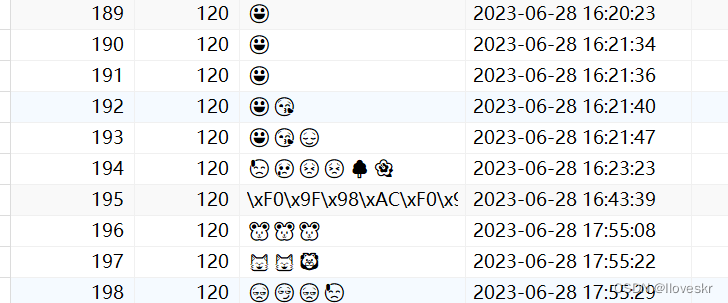
将表情存入数据库
概念: 表情是一种比较特殊的字符串,为unicode编码,unicode编码要存入数据库一般情况下,是存不了的,有两种解决方式,一种将数据表编码方式改为unicode编码方式,但是这种情况适用于功能刚开始设计…...
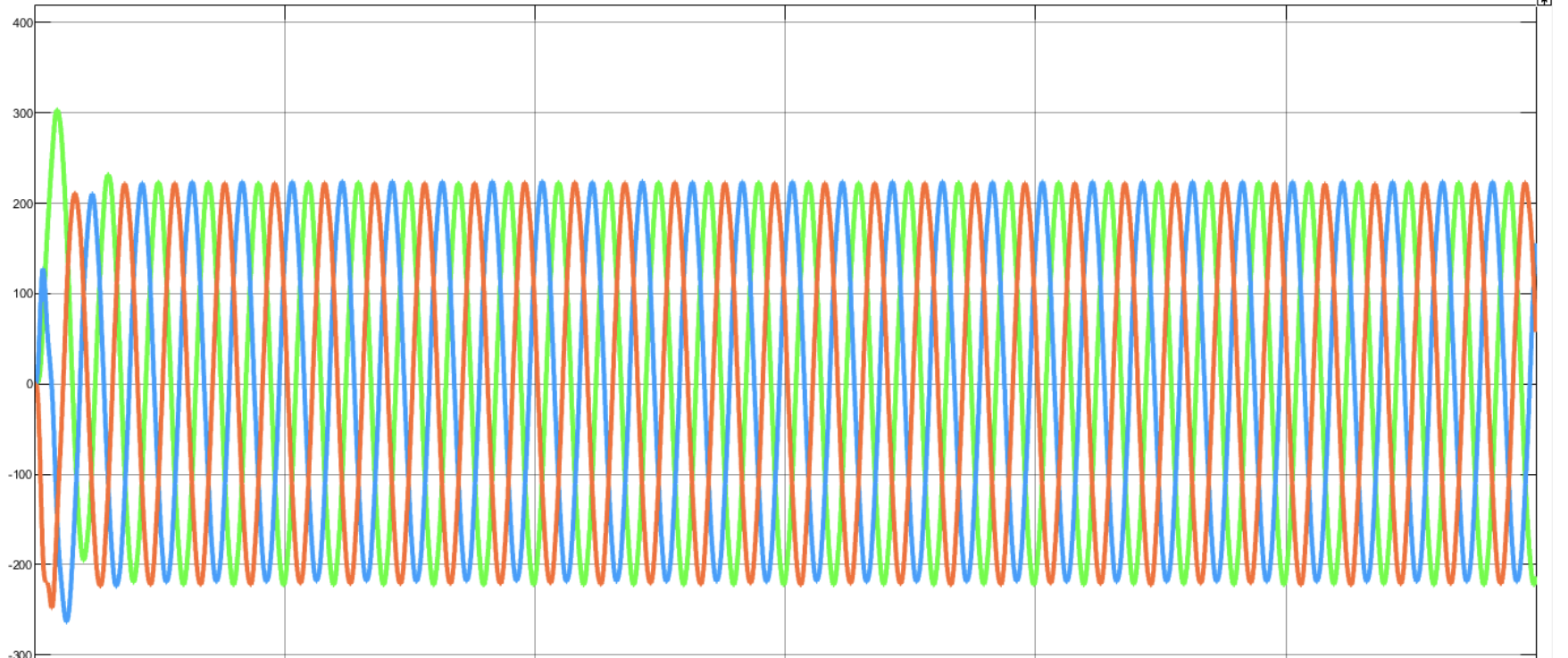
H桥级联型五电平三相逆变器Simulink仿真模型
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
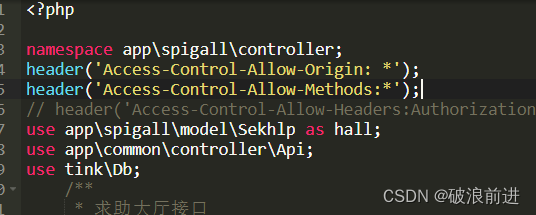
后端解决跨域(极速版)
header(Access-Control-Allow-Origin: *); header(Access-Control-Allow-Methods:*); 代表接收全部的请求,"POST,GET"//允许访问的方式 指定域,如http://172.20.0.206//宝塔的域名,注意不是:http://wang.jingyi.icu等…...
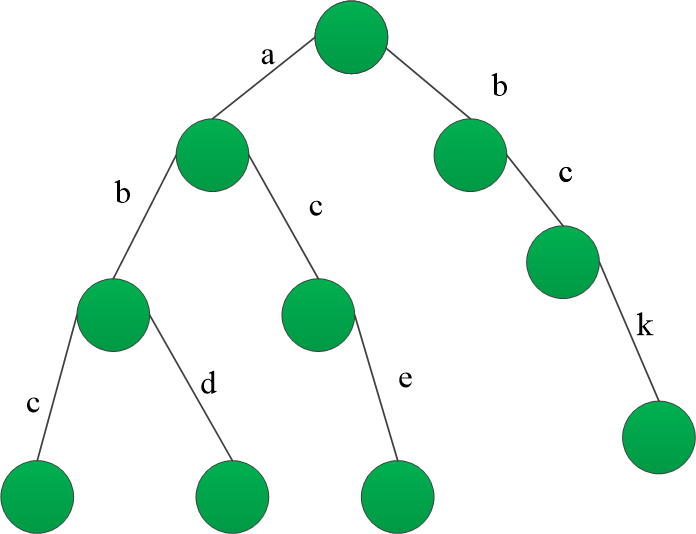
数据结构与算法-前缀树
数据结构与算法-前缀树详解 1 何为前缀树 2 前缀树的代码表示及相关操作 1 何为前缀树 前缀树 又称之为字典树,是一种多路查找树,多路树形结构,是哈希树的变种,和hash效率有一拼,是一种用于快速检索的多叉树结构。 性质:不同字符串的相同…...
DirectX12_Windows_GameDevelop_3:Direct3D的初始化
引言 查看龙书时发现,第四章介绍预备知识的代码不太利于学习。因为它不像是LearnOpenGL那样从头开始一步一步教你敲代码,导致你没有一种整体感。如果你把它当作某一块的代码进行学习,你跟着敲会发现,总有几个变量是没有定义的。这…...
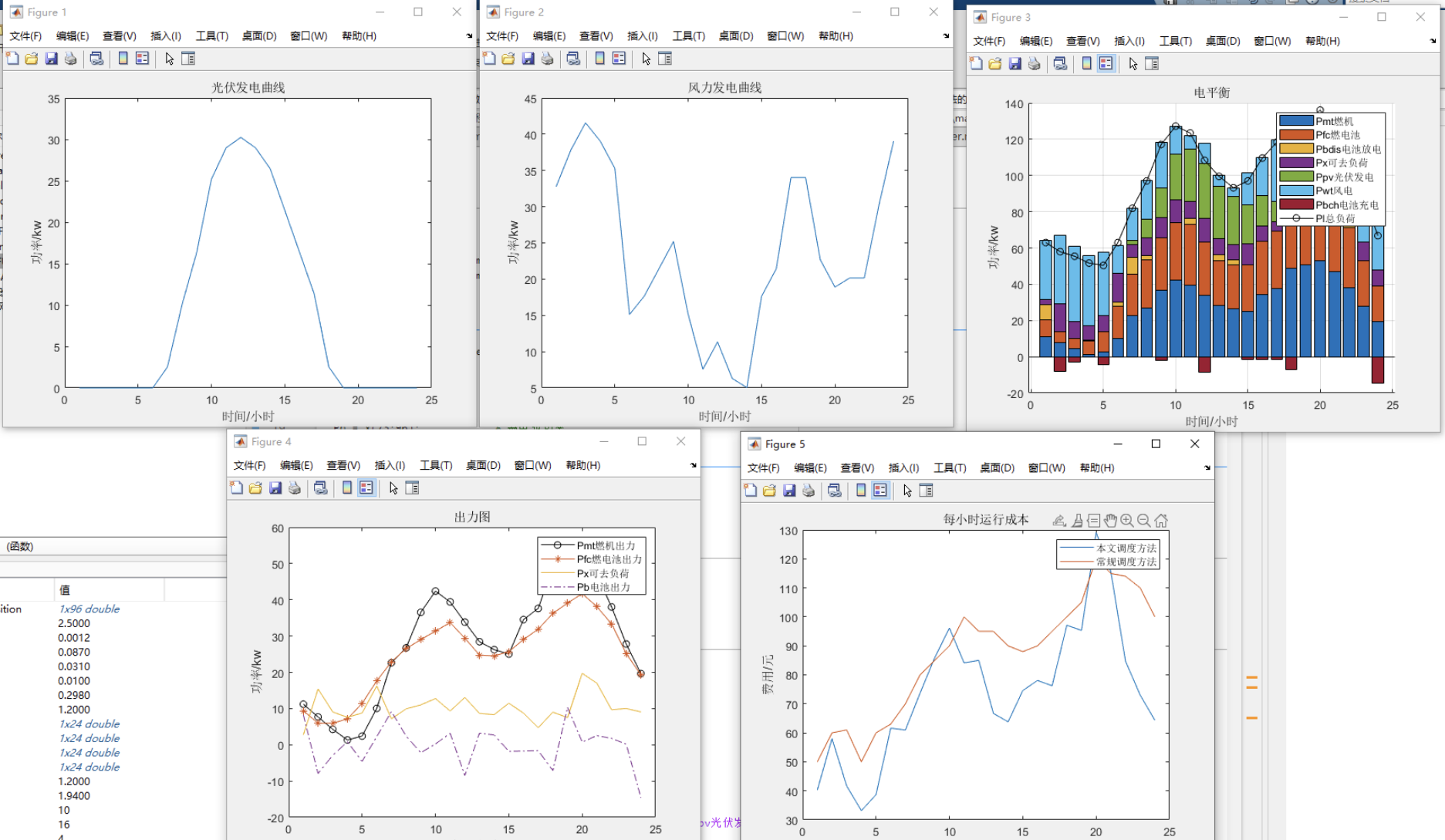
基于粒子群优化算法、鲸鱼算法、改进的淘沙骆驼模型算法(PSO/SSA/tGSSA)的微电网优化调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
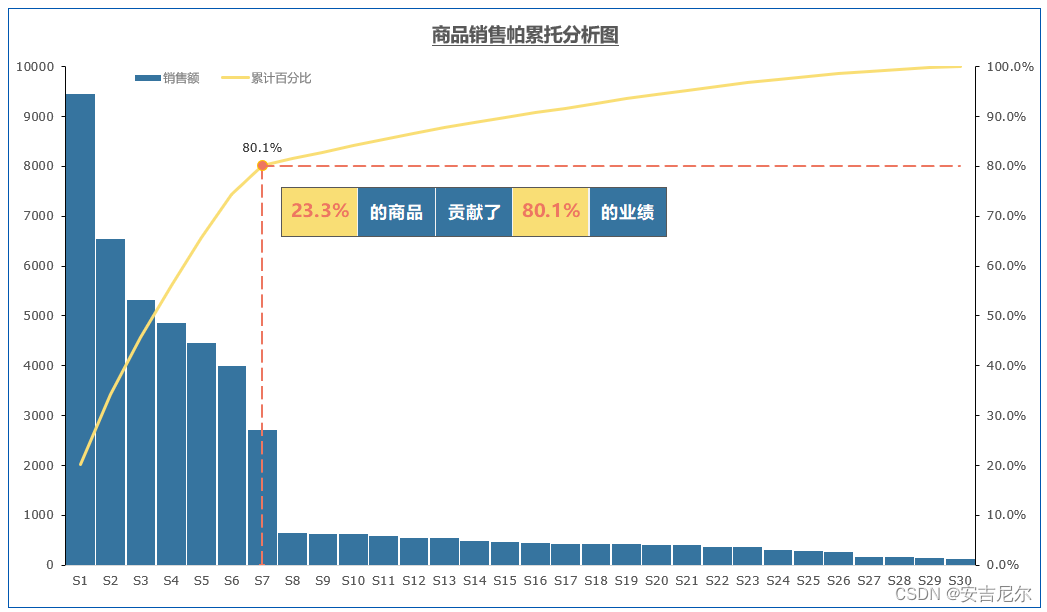
数据分析篇-数据认知分析
一简介 数据认知分析,实际是对数据的整体结构和分布特征进行分析,是对整个数据外在的认识,也是数据分析的第一步。对于数据认知的分析,一般会考虑分散性、位置特性、变量的相关性等,一般会考虑平均数、方差、极差、峰…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
