数学建模预测模型MATLAB代码大合集及皮尔逊相关性分析(无需调试、开源)
已知2010-2020数据,预测2021-2060数据
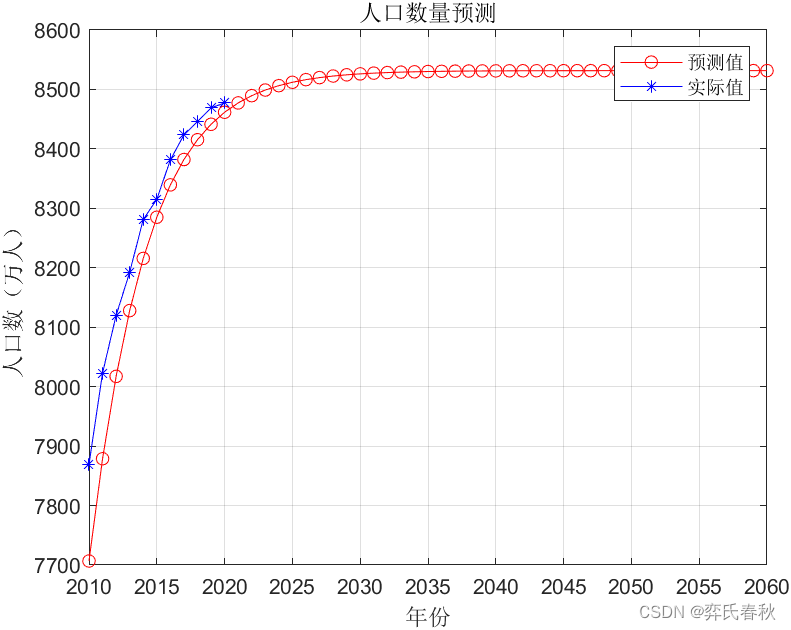
一、Logistic预测人口
%%logistic预测2021-2060年结果
clear;clc;
X=[7869.34, 8022.99, 8119.81, 8192.44, 8281.09, 8315.11, 8381.47, 8423.50, 8446.19, 8469.09, 8477.26];
n=length(X)-1;
for t=1:nZ(t)=(X(t+1)-X(t))/X(t+1);
end
X1=[ones(n,1) X(1:n)'];
Y=Z';
[B,Bint,r,rint,stats]=regress(Y,X1);%最小二乘(OLS)
gamma=B(1,1);
beta=B(2,1);
b=log(1-gamma);
c=beta/(exp(b)-1);
a=exp((sum(log(1./X(1:n)-c))-n*(n+1)*b/2)/n);
XX=2010:2060;
YY=1./(c+a*exp(b*([XX-2010])));
plot(XX,YY,'r-o')
hold on
plot(XX(1:length(X)),X,'b-*')
legend('预测值','实际值')
xlabel('年份');ylabel('人口数(万人)');
title('人口数量预测')
set(gca,'XTick',[2010:5:2060])
grid on
format short;
forecast=YY(end-40:end);%2021-2060人口的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X);%平均相对差值
a,b,c
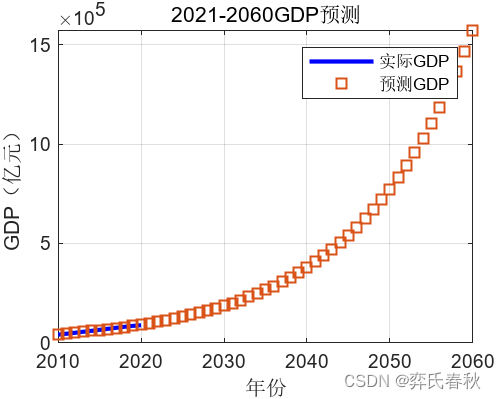
二、灰色预测GDP
%%灰色预测模型预测某区2021-2060年GDP量变化
clc;clear;
%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
c = [a b]';
%原始数列(这里我们输入历史碳排放数据)
A = [41383.87,45952.65,50660.20,55580.11,60359.43,65552.00,70665.71,75752.20,80827.71,85556.13,88683.21];
%级比检验
n = length(A);
min=exp(-2/(n+1));
max=exp(2/(n+1));
for i=2:n
ans(i)=A(i-1)/A(i);
end
ans(1)=[];
for i=1:(n-1)
if ans(i)<max&ans(i)>min
else
fprintf('第%d个级比不在标准区间内',i)
disp(' ');
end
end
%对原始数列 A 做累加得到数列 B
B = cumsum(A);
%对数列 B 做紧邻均值生成
for i = 2:n
C(i) = (B(i) + B(i - 1))/2;
end
C(1) = [];
%构造数据矩阵
B = [-C;ones(1,n-1)];
Y = A; Y(1) = []; Y = Y';
%使用最小二乘法计算参数 a(发展系数)和b(灰作用量)
c = inv(B*B')*B*Y;
c = c';
a = c(1);
b = c(2);
%预测后续数据
F = []; F(1) = A(1);
for i = 2:(n+40)
F(i) = (A(1)-b/a)/exp(a*(i-1))+ b/a;
end
%对数列 F 累减还原,得到预测出的数据
G = []; G(1) = A(1);
for i = 2:(n+40)
G(i) = F(i) - F(i-1); %得到预测出来的数据
end
disp('预测数据为:');
G
%模型检验
H = G(1:n);
%计算残差序列
epsilon = A - H;
%法一:相对残差Q检验
%计算相对误差序列
delta = abs(epsilon./A);
%计算相对误差平均值Q
disp('相对残差Q检验:')
Q = mean(delta)
%法二:方差比C检验disp('方差比C检验:')
C = std(epsilon, 1)/std(A, 1)
%法三:小误差概率P检验
S1 = std(A, 1);
tmp = find(abs(epsilon - mean(epsilon))< 0.6745 * S1);
disp('小误差概率P检验:')
P = length(tmp)/n
%绘制曲线图
t1 = 2010:2020;
t2 = 2010:2060;
plot(t1, A,'-b','LineWidth',2);
hold on;
plot(t2, G, 's','LineWidth',1);
xlabel('年份'); ylabel('GDP(亿元)');
legend('实际GDP','预测GDP');
title('2021-2060GDP预测');
grid on;
三、BP神经网络预测
选取2000-2017年x省碳排放量为训练集,2018-2022x省碳排放量作为测试集,以此来预测2023-2026年x省碳排放量。设置训练次数为 1000次,学习速率为0.2;对该训练集BP神经网络模型拟合后模型的训练样本、验 证样本和测试样本的均方误差分别是0.000012、0.0023、0.0042,整体的误差为 0.0082203,因此训练好的BP神经网络模型的预测精度较高。训练好的BP神经网络 神经模型的结果如图3所示
clear allclcclf%% 1,读取数据,并做归一化处理
input_1=[2391,2487,2588,2683,3150,3513,3751,3969,4384,4653,4482,5366,6238,6515,6647,6704,6806,6682,6346,6253,6513,7120,7597];n=length(input_1);row=4; %通过前四年数据,预测第五年
input=zeros(4,n-row);for i =1:rowinput(i,:)=input_1(i:n-row+i-1);endoutput=input_1(row+1:end);[inputn,inputps]=mapminmax(input);[outputn,outputps]=mapminmax(output);%% 2,划分训练集和测试集
inputn_train=inputn(:,1:n-row-5);inputn_test=inputn(:,n-row-4:end);outputn_train=outputn(1:n-row-5);outputn_test=outputn(n-row-4:end);%% 3,构建BP神经网络
hiddennum=10;%隐含层节点数量经验公式p=sqrt(m+n)+anet=newff(inputn_train,outputn_train,hiddennum,{'tansig','purelin'},'trainlm'); %tansig :正切 S 型传递函数。purelin:线性传递函数。trainlm:Levenberg-Marquardt 算法
%% 4,网络参数配置
net.trainParam.epochs=1000;net.trainParam.lr=0.2;%% 5,BP神经网络训练
[net,tr]=train(net,inputn_train,outputn_train);%% 6,仿真计算
resultn=sim(net,inputn_test);%% 7,计算与测试集之间误差
result=mapminmax('reverse',resultn,outputps);output_test=mapminmax('reverse',outputn_test,outputps);error=result-output_test;rmse=sqrt(error*error')/length(error);figure(1)plot(output_test,'b')hold onplot(result,'r*');hold on
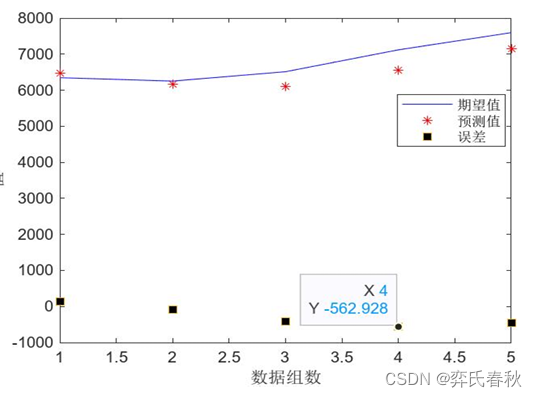
plot(error,'s','MarkerFaceColor','k')legend('期望值','预测值','误差')xlabel('数据组数')ylabel('值')%% 8,预测未来四年碳排放
pn=3;[p_in,ps]=mapminmax(input_1(n-row+1:end));p_in=p_in';p_outn=zeros(1,pn);for i = 1:pnp_outn(i)=sim(net,p_in);p_in=[p_in(2:end);p_outn(i)];endp_out=mapminmax('reverse',p_outn,ps)figure(2)plot(2000:2022,input_1,'k--o')hold onplot(2018:2022,result,'b--*')hold onplot(2023:2026,[result(end),p_out],'r--+')legend('实际值','拟合值','预测值')
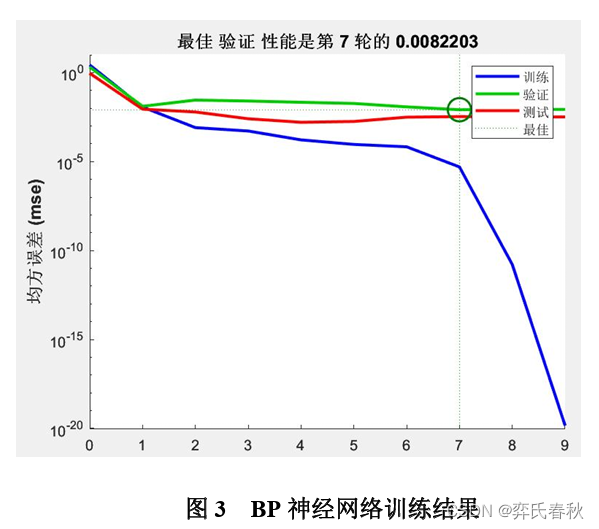
从图3看出,验证样本和测试样本的均方误差收敛到近 时达到最小,这时训练出的BP神经网络模型是最优的。利用BP神经网络模型预测2023-2026 年x省碳排放量分别 是7149.39 万吨、7556.6 万吨、7441.1 万吨、7479.1 万吨。x省碳排放量实际值、拟合值、预测值的变化趋势见下图。
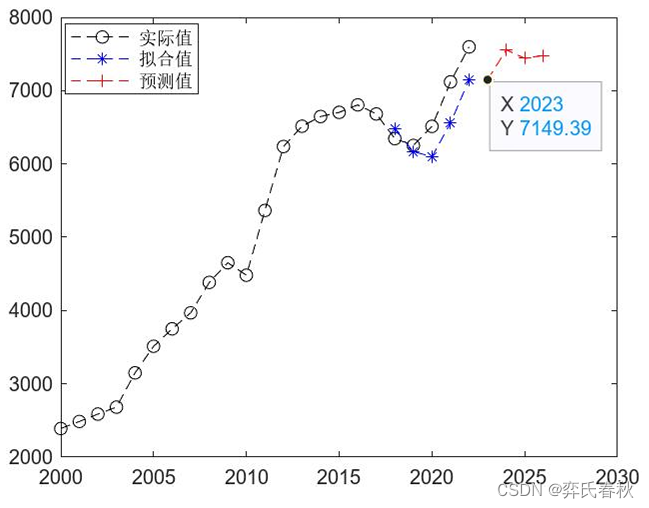
2018-2022 年实际建筑碳排放量和预测得到的全过程碳排放量的误差图,如下图所示:
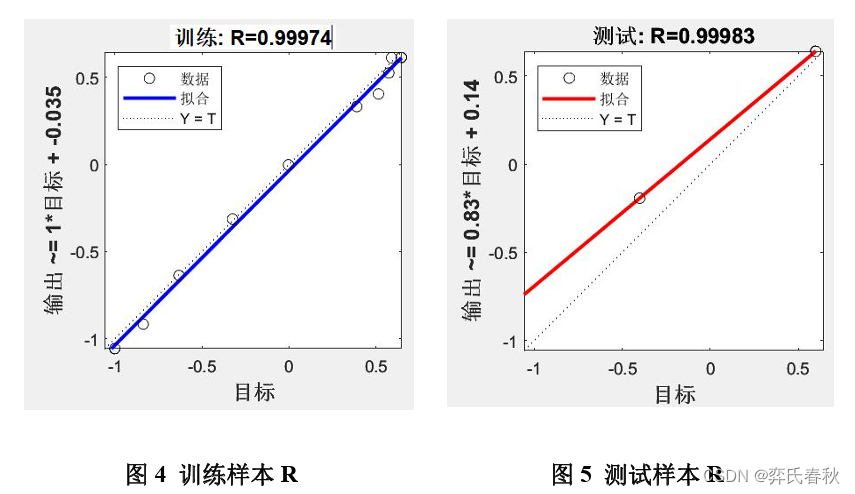
训练完成BP神经网络模型后可以得到训练集、验证集、测试集以及整体结果 的数据相关性。训练样本、验证样本、测试样本的预测输出和目标输出的相关系 数分别为0.99974、0.9935、0.99983,整体的相关系数为0.99238,如图4,5,6,7 所示。BP神经网络拟合结果较好。
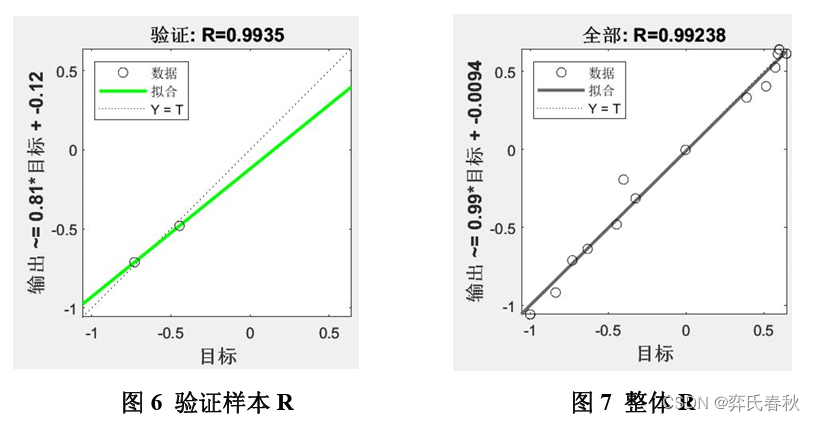
四、皮尔逊相关性分析代码
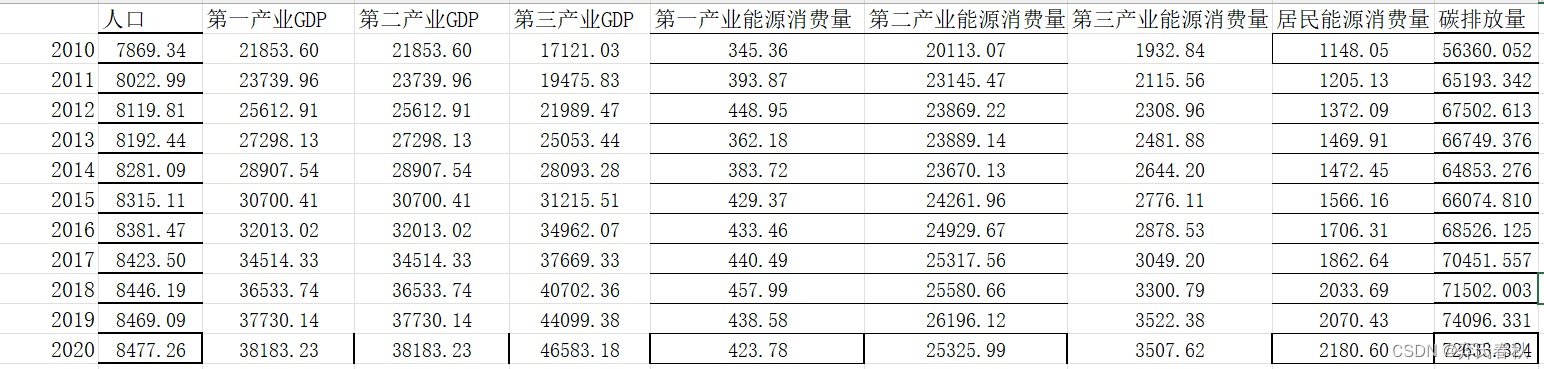
将该xiu.xlsx放到一新建文件夹中,然后在MATLAB中导入该表格(点击绿色箭头文件夹)
%%皮尔逊相关性分析矩阵代码
clc
clear all
data=xlsread('xiu.xlsx',1,'B2:J12');
figure
% 求维度之间的相关系数
rho = corr(data, 'type','pearson');
% 绘制热图
string_name={'人口','第一产业GDP','第二产业GDP','第三产业GDP','第一产业能源消费量','第二产业能源消费量','第三产业能源消费量','居民生活能源消费量','碳排放总量'};
xvalues = string_name;
yvalues = string_name;
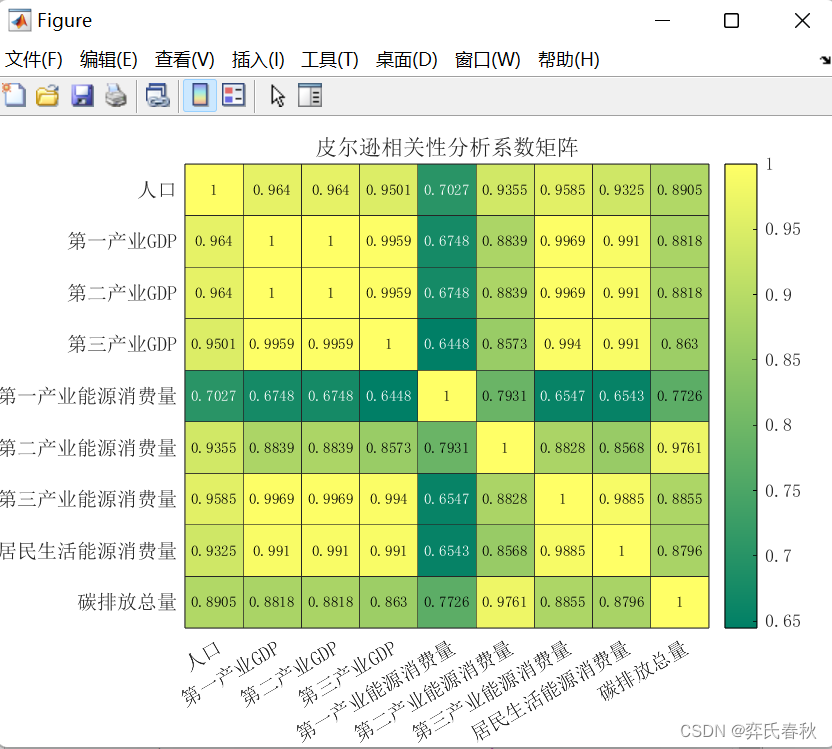
h = heatmap(xvalues,yvalues, rho, 'FontSize',10, 'FontName','宋体');
h.Title = '皮尔逊相关性分析系数矩阵';
colormap summerfigure
% 可以自己定义颜色块
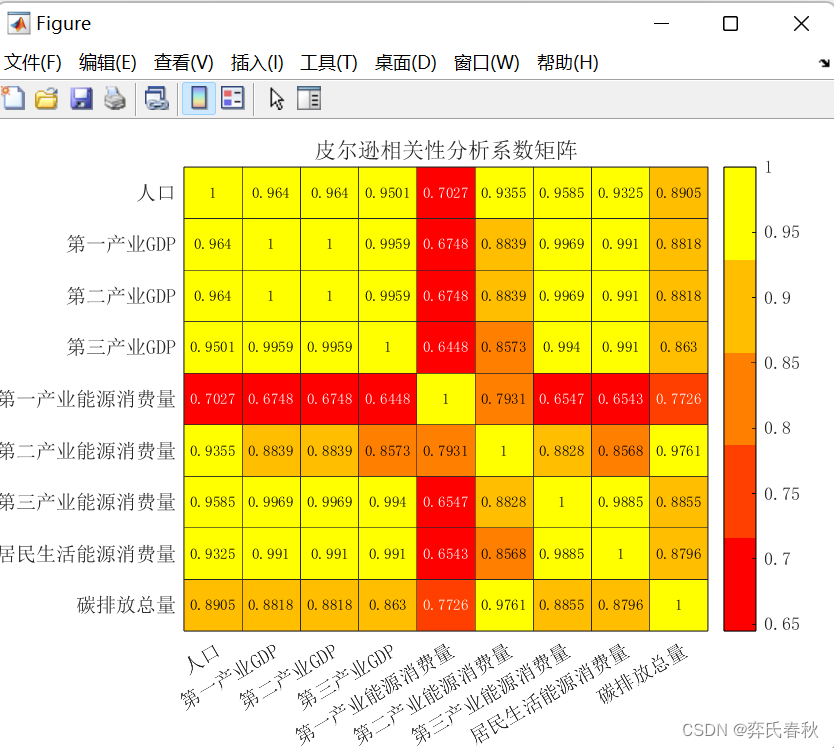
H = heatmap(xvalues,yvalues, rho, 'FontSize',10, 'FontName','宋体');
H.Title = '皮尔逊相关性分析系数矩阵';
colormap(autumn(5))%设置颜色个数
colormap函数用于设置当前图形的颜色映射。常见颜色映射有:summer\autumn\winter\spring\cool\hot\hsv\jet
相关文章:

数学建模预测模型MATLAB代码大合集及皮尔逊相关性分析(无需调试、开源)
已知2010-2020数据,预测2021-2060数据 一、Logistic预测人口 %%logistic预测2021-2060年结果 clear;clc; X[7869.34, 8022.99, 8119.81, 8192.44, 8281.09, 8315.11, 8381.47, 8423.50, 8446.19, 8469.09, 8477.26]; nlength(X)-1; for t1:nZ(t)(X(t1)-X(t))/X(t1…...

泛型擦除是什么?
泛型擦除的主要特点包括: 编译时类型检查:在编写泛型代码时,编译器会对泛型类型参数进行类型检查,以确保类型安全。这意味着在编译时会捕获许多类型错误,避免了运行时类型错误。因为泛型其实只是在编译器中实现的而虚拟…...

阿里云轻量应用服务器有月流量限制吗?
阿里云轻量应用服务器限制流量吗?部分限制,2核2G3M和2核4G4M这两款轻量应用服务器不限制月流量,其他的轻量服务器套餐有月流量限制。 腾讯云轻量应用服务器价格便宜,活动页面:aliyunbaike.com/go/tencent 细心的同学看…...

mysql面试题25:数据库自增主键可能会遇到什么问题?应该怎么解决呢?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:数据库自增主键可能会遇到什么问题? 数据库自增主键可能遇到的问题: 冲突问题:自增主键是通过自动递增生成的唯一标识符,但在某些情况下可能会…...

学习css 伪类:has
学习抖音: 渡一前端提薪课 首先我们看下:has(selector)是什么 匹配包含(相对于 selector 的 :scope)指定选择器的元素。可以认为 selector 的前面有一个看不见的 :scope 伪类。它的强大之处是,可以实现父选择器和前面兄弟选择器…...
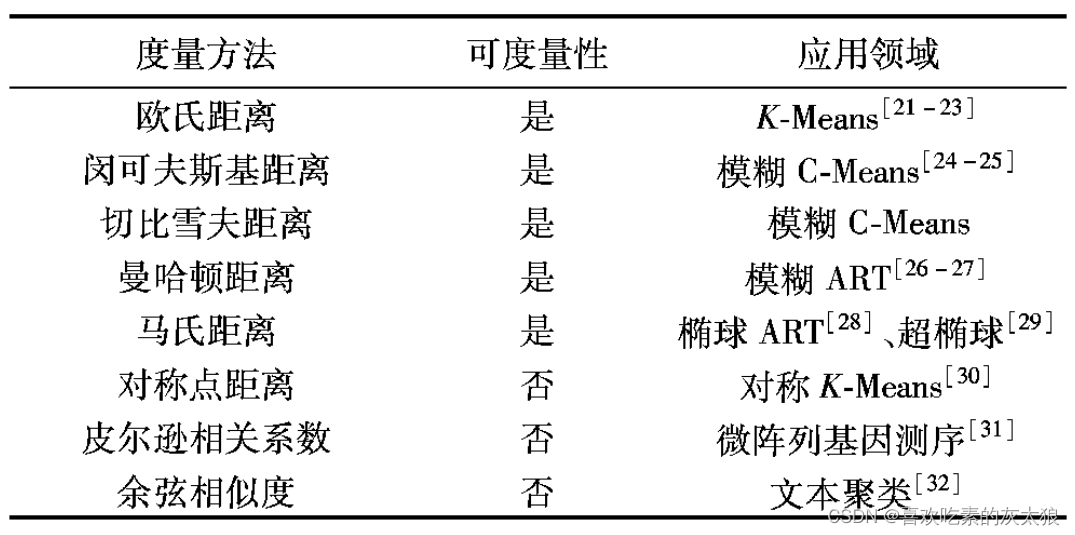
矩阵的相似性度量的常用方法
矩阵的相似性度量的常用方法 1,欧氏距离 欧式距离是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式。 (1)二维平面上的点 a ( x 1 , y 1 ) a(x_1,y_1) a(x1,y1)和点 b ( x 2 , y 2 ) b(x_2,y_2) b(x2,y2)的欧式距离为 d ( x …...

Java之TCP,UDP综合小练习一
4. 综合练习 练习一:多发多收 需求: 客户端:多次发送数据 服务器:接收多次接收数据,并打印 代码示例: public class Client {public static void main(String[] args) throws IOException {//客户端&…...
Docker 日志管理 - ELK
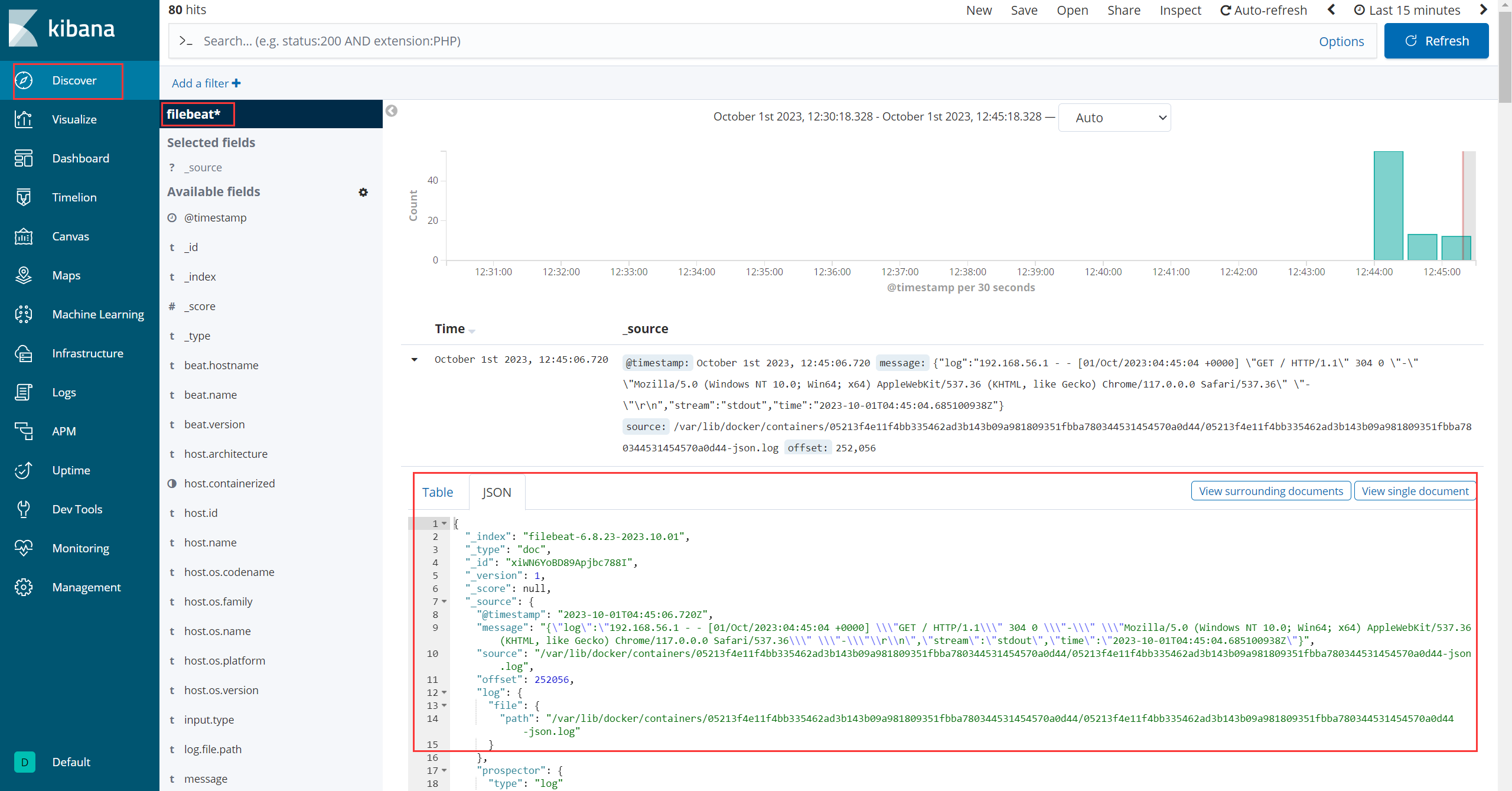
Author:rab 目录 前言一、Docker 日志驱动二、ELK 套件部署三、Docker 容器日志采集3.1 部署 Filebeat3.2 配置 Filebeat3.3 验证采集数据3.4 Kibana 数据展示3.4.1 创建索引模式3.4.2 Kibana 查看日志 总结 前言 如何查看/管理 Docker 运行容器的日志?…...
windows系统下利用python对指定文件夹下面的所有文件的创建时间进行修改
windows系统下利用python对指定文件夹下面的所有文件的创建时间进行修改 不知道其他的朋友们有没有这个需求哈,反正咱家是有这个需求 需求1、当前有大量的文件需要更改文件生成的时间,因为不可告知的原因,当前的文件创建时间是不能满足使用的…...

线性表的链式表示——单链表;头插,尾插,按值查找,按序号查找,插入,删除;
#include <iostream> #include <algorithm>//fill() #define InitSize 5using namespace std;/*线性表:链式表示——单链表;头插,尾插,按值查找,按序号查找,插入,删除*/ typedef st…...

【Spring Cloud系统】- Zookeer特性与使用场景
【Spring Cloud系统】- Zookeer特性与使用场景 一、概述 Zookeeper是一个分布式服务框架,是Apache Hadoop的一个子项目,它主要是用来解决分布式应用中经常遇到的一些数据管理问题。如:统一命名服务、状态同步服务、集群管理、分布式应用配置…...
最新AI智能创作系统源码SparkAi系统V2.6.3/AI绘画系统/支持GPT联网提问/支持Prompt应用/支持国内AI模型
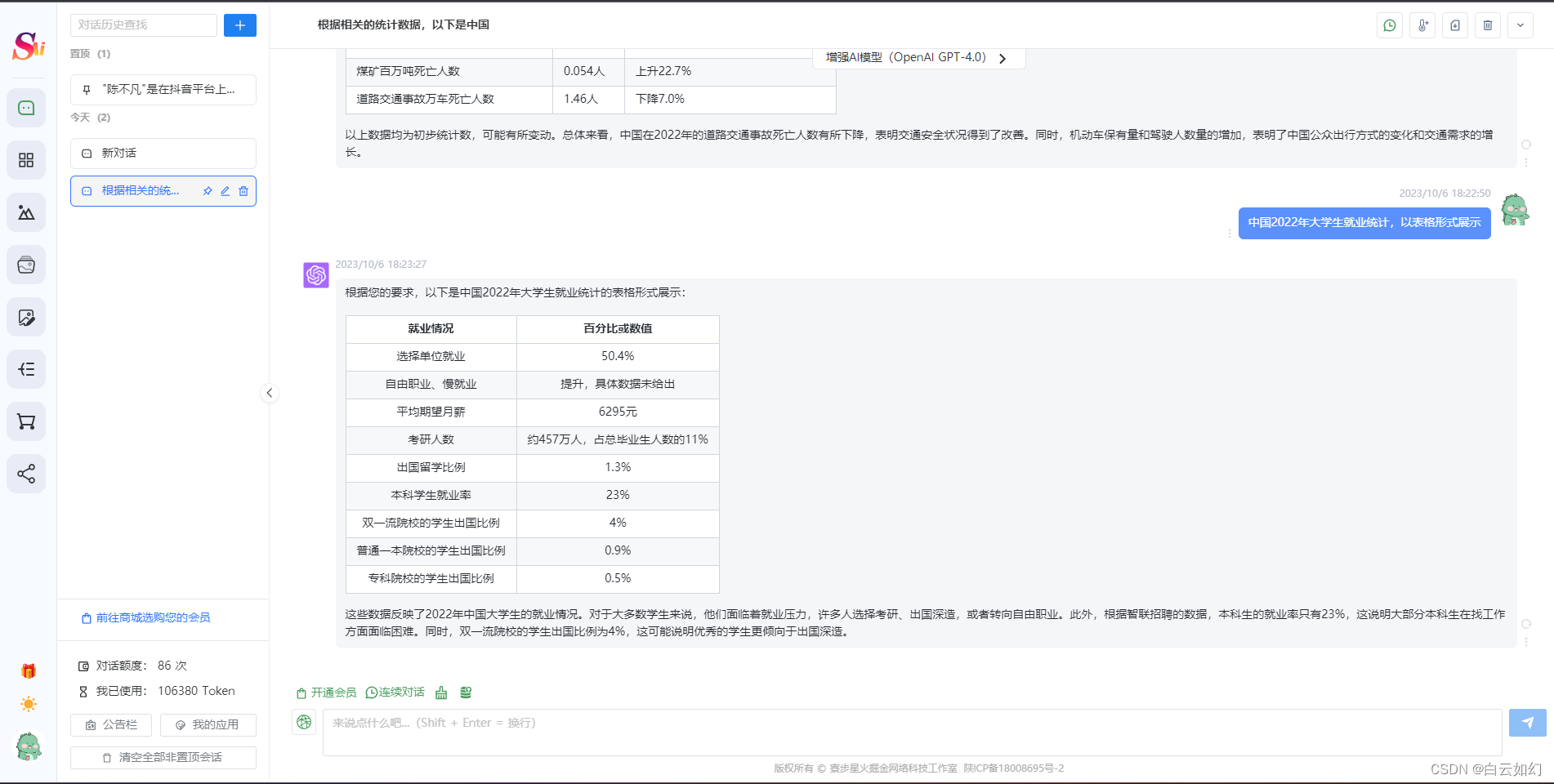
一、智能AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统,已支持OpenAIGPT全模型国内AI全模型,已支持国内AI模型 百度文心一言、微软Azure、阿里云通义千问模型、清华智谱AIChatGLM、科大讯飞星火大模型等。本期针对源码…...
R | R包默认安装路径的查看及修改
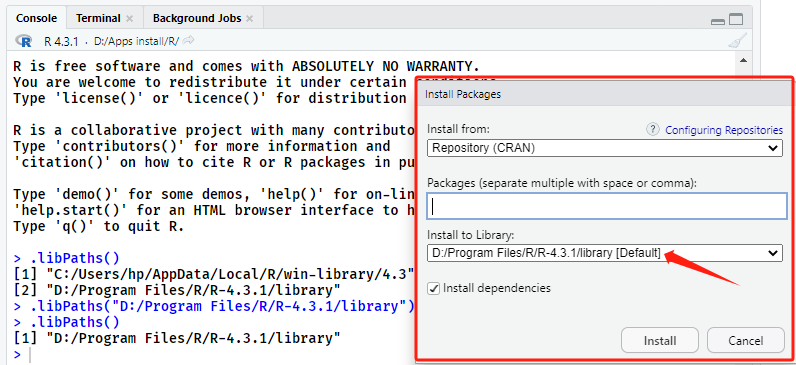
R | R包默认安装路径的查看及修改 一、R包安装位置查看二、已安装R包查询三、R包安装位置修改四、R包安装位置永久修改 在【R: R package安装的几种方式】【R: R版本更新及R包迁移(详细步骤)】两篇文章中介绍过R包的常见安装方式,以及在不同R…...

将conda虚拟环境打包并集成到singularity镜像中
1. 使用yml文件打包 conda activate your_env conda env export > environment.yml编写cond.def文件 Bootstrap: dockerFrom: continuumio/miniconda3%filesenvironment.yml%post/opt/conda/bin/conda env create -f environment.yml%runscriptexec /opt/conda/envs/$(hea…...

Android Studio 是如何和我们的手机共享剪贴板的
背景 近期完成了target33的项目适配升级,随着AGP和gradle的版本升级,万年老版本Android Studio(后文简称AS)也顺便升级到了最新版Android Studio Giraffe | 2022.3.1,除了新UI外,最让我好奇的是这次的Running Devices功能(官方也称为Device mirroring)可以控制真机了. 按照操…...

大数据面试题:Spark和MapReduce之间的区别?各自优缺点?
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答: 1)spark和maprecude的对比;2)mapreduce与spark优劣好处 问过的一些公司:阿里云…...

【开发篇】十八、SpringBoot整合ActiveMQ
文章目录 1、安装ActiveMQ2、整合3、发送消息到队列4、使用消息监听器对消息队列监听5、流程性业务消息消费完转入下一个消息队列6、发布订阅模型 1、安装ActiveMQ docker安装 docker pull webcenter/activemqdocker run -d --name activemq -p 61616:61616 -p 8161:8161 webce…...

QTcpSocket 接收数据实时性问题
一、开发背景 使用 Qt 的 QTcpSocket 接收数据的时候发现数据接收出现粘包的现象,并且实时性很差,通过日志的时间戳发现数据接收的误差在 100ms 以内。 二、开发环境 Qt5.12.2 QtCreator4.8.2 三、实现步骤 在 socket 连接的槽函数设置接收延时时间&…...

前端el-select 单选和多选
el-select单选 <el-form-item label"部门名称" prop"departId"><el-select v-model"dataForm.departId" placeholder"请选择" clearable:style{ "width": "100%" } :multiple"false" filtera…...
【MySQL】Linux 中 MySQL 环境的安装与卸载
文章目录 Linux 中 MySQL 环境的卸载Linux 中 MySQL 环境的安装 Linux 中 MySQL 环境的卸载 在安装 MySQL 前,我们需要先将系统中以前的环境给卸载掉。 1、查看以前系统中安装的 MySQL rpm -qa | grep mysql2、卸载这些 MySQL rpm -qa | grep mysql | args yum …...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
