多校联测11 模板题
题目大意
给你四个整数 n , m , s e e d , w n,m,seed,w n,m,seed,w,其中 n , m n,m n,m为两个多项式 A ( x ) = ∑ i = 0 n a i x i A(x)=\sum\limits_{i=0}^na_ix^i A(x)=i=0∑naixi和 B ( x ) = ∑ i = 0 m b i x i B(x)=\sum\limits_{i=0}^mb_ix^i B(x)=i=0∑mbixi的最高次数, s e e d , w seed,w seed,w是用来生成 a i a_i ai和 b i b_i bi的参数。
设 C ( x ) = A ( x ) B ( x ) = ∑ i = 0 n + m c i x i C(x)=A(x)B(x)=\sum\limits_{i=0}^{n+m}c_ix^i C(x)=A(x)B(x)=i=0∑n+mcixi。
有 q q q次询问,第 i i i次输入 l i , r i l_i,r_i li,ri,求 ∑ j = l i r i c j \sum\limits_{j=l_i}^{r_i}c_j j=li∑ricj对 1145141999 1145141999 1145141999( 1145141999 = 2 × 7 × 11 × 13 × 17 × 33647 + 1 1145141999=2\times 7\times 11\times 13\times 17\times 33647+1 1145141999=2×7×11×13×17×33647+1,是一个质数)取模后的值。
构造 a i a_i ai和 b i b_i bi的代码如下,可以对其进行修改来完成此题。
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long u64;
const int p=1145141999;
int a[10000005],b[10000005];
int n,m,q,w;
u64 seed;
u64 rnd()
{u64 x = seed;x ^= x << 13;x ^= x >> 7;x ^= x << 17;return seed = x;
}
int main(){scanf("%d%d%llu%d",&n,&m,&seed,&w);scanf("%d",&q);for(int i=0;i<=n;++i)a[i]=rnd()%w;for(int i=0;i<=m;++i)b[i]=rnd()%w;int l,r;for(int i=1;i<=q;++i){scanf("%d%d",&l,&r);}return 0;
}
1 ≤ n ≤ 6 × 1 0 6 , 1 ≤ q ≤ 25 , 1 ≤ w ≤ 1145141999 1\leq n\leq 6\times 10^6,1\leq q\leq 25,1\leq w\leq 1145141999 1≤n≤6×106,1≤q≤25,1≤w≤1145141999
题解
C ( x ) = A ( x ) B ( x ) = ∑ i = 0 n + m ( ∑ j = 0 i a j b i − j ) x i C(x)=A(x)B(x)=\sum\limits_{i=0}^{n+m}(\sum\limits_{j=0}^ia_jb_{i-j})x^i C(x)=A(x)B(x)=i=0∑n+m(j=0∑iajbi−j)xi
也就是说, c i = ∑ j = 0 i a j b i − j c_i=\sum\limits_{j=0}^ia_jb_{i-j} ci=j=0∑iajbi−j。
那么, ∑ i = 0 t c i = ∑ i = 0 t ∑ j = 0 i a j b i − j = ∑ j = 0 t a j ∑ i = 0 t − j b i \sum\limits_{i=0}^tc_i=\sum\limits_{i=0}^t\sum\limits_{j=0}^ia_jb_{i-j}=\sum\limits_{j=0}^ta_j\sum\limits_{i=0}^{t-j}b_i i=0∑tci=i=0∑tj=0∑iajbi−j=j=0∑taji=0∑t−jbi
令 b i b_i bi的前缀和为 s u m i {sum}_i sumi, S ( t ) = ∑ i = 0 t a i s u m t − i S(t)=\sum\limits_{i=0}^ta_i{sum}_{t-i} S(t)=i=0∑taisumt−i,则答案为 S ( r ) − S ( l − 1 ) S(r)-S(l-1) S(r)−S(l−1)。
求 S ( t ) S(t) S(t)的时间复杂度为 O ( n ) O(n) O(n),所以总时间复杂度为 O ( n q ) O(nq) O(nq)。
code
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long u64;
const long long p=1145141999;
int a[20000005],b[20000005],sum[20000005];
int n,m,q,w;
u64 seed;
u64 rnd()
{u64 x = seed;x ^= x << 13;x ^= x >> 7;x ^= x << 17;return seed = x;
}
long long gt(int t){long long re=0;for(int i=0;i<=t;i++){re=(re+1ll*a[i]*sum[t-i])%p;}return re;
}
int main(){scanf("%d%d%llu%d",&n,&m,&seed,&w);scanf("%d",&q);for(int i=0;i<=n;++i)a[i]=rnd()%w;for(int i=0;i<=m;++i)b[i]=rnd()%w;sum[0]=b[0];for(int i=1;i<=n+m;i++) sum[i]=(1ll*sum[i-1]+b[i])%p;int l,r;for(int i=1;i<=q;++i){scanf("%d%d",&l,&r);printf("%lld\n",(gt(r)-gt(l-1)+p)%p);}return 0;
}
相关文章:

多校联测11 模板题
题目大意 给你四个整数 n , m , s e e d , w n,m,seed,w n,m,seed,w,其中 n , m n,m n,m为两个多项式 A ( x ) ∑ i 0 n a i x i A(x)\sum\limits_{i0}^na_ix^i A(x)i0∑naixi和 B ( x ) ∑ i 0 m b i x i B(x)\sum\limits_{i0}^mb_ix^i B(x)i0∑mbixi…...
Linux SSH连接远程服务器(免密登录、scp和sftp传输文件)
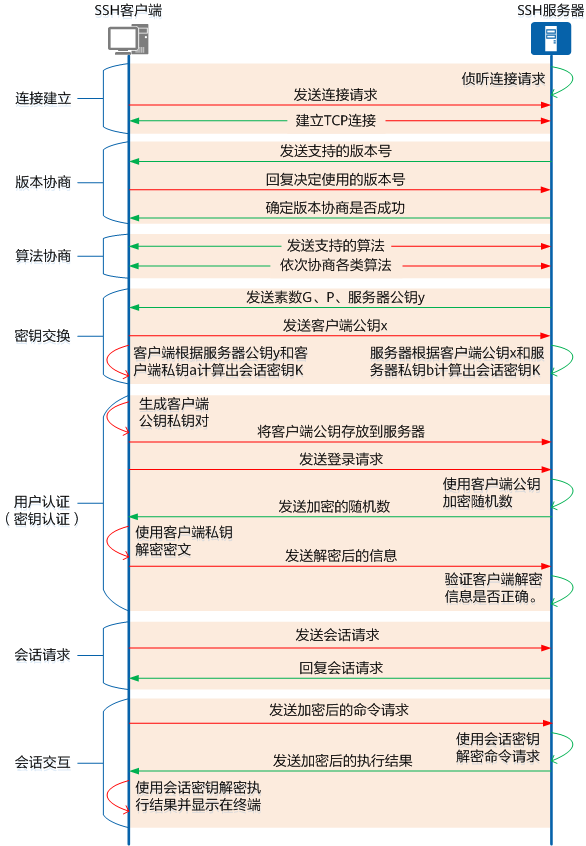
1 SSH简介 SSH(Secure Shell,安全外壳)是一种网络安全协议,通过加密和认证机制实现安全的访问和文件传输等业务。传统远程登录和文件传输方式,例如Telnet、FTP,使用明文传输数据,存在很多的安全…...
从0开始python学习-30.selenium frame子页面切换
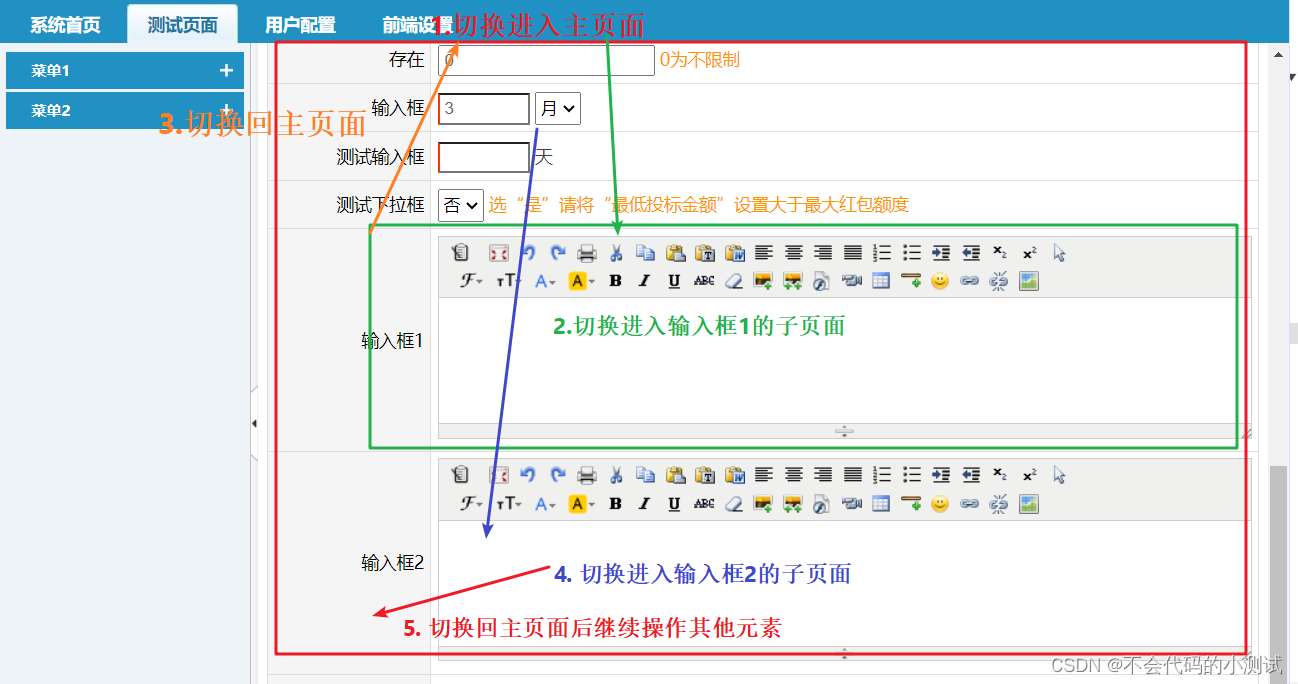
目录 1. frame切换逻辑 2. 多层子页面情况进行切换 3. 多个子页面相互切换 1. frame切换逻辑 1.1. 子页面的类型一般分为两种 frame标签 iframe标签 1.2. 子页面里面的元素和主页面的元素是相互独立 子页面元素需要进去切换才能操作 如果已经进入子页面,那么…...
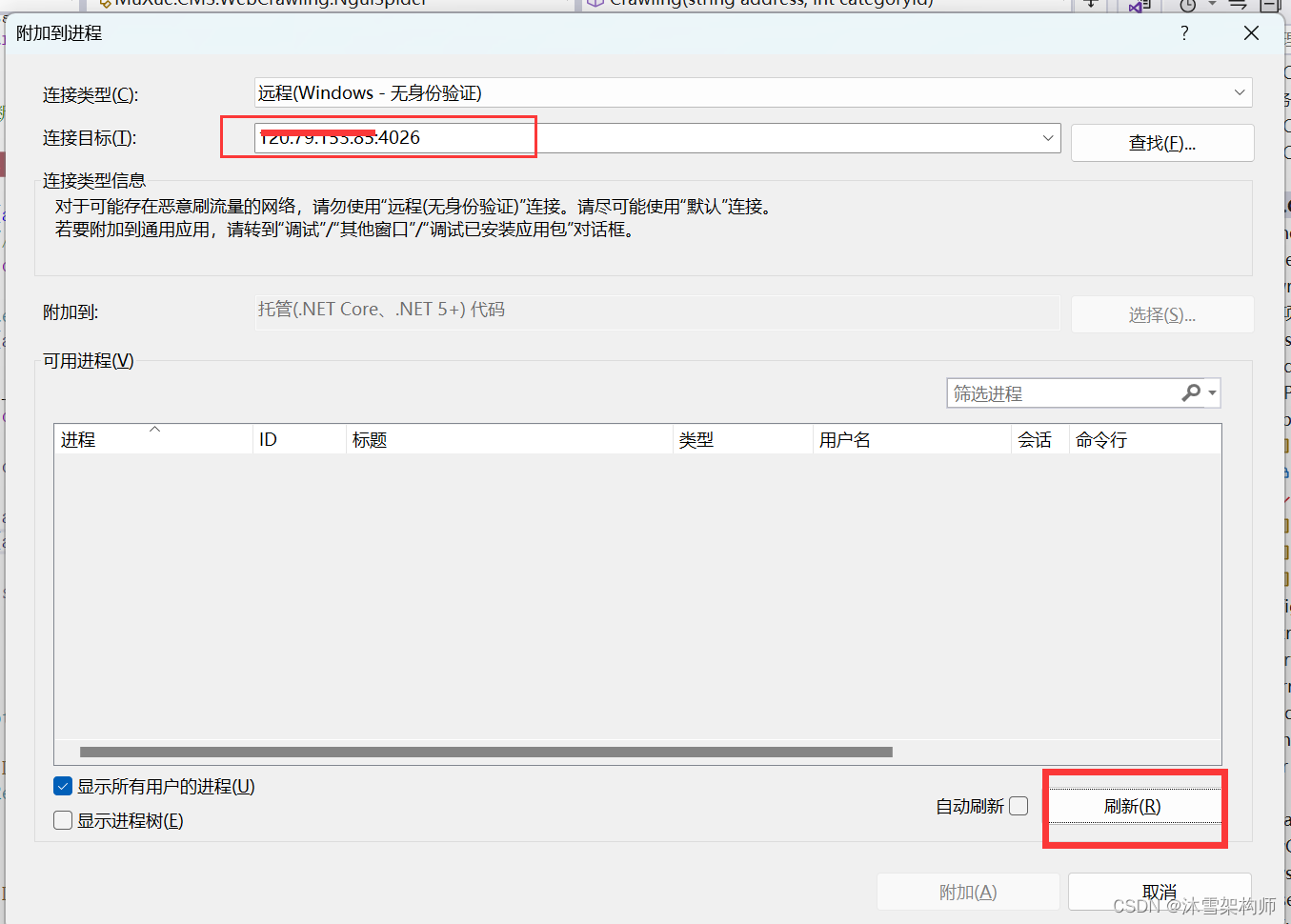
asp.net core 远程调试
大概说下过程: 1、站点发布使用Debug模式 2、拷贝到远程服务器,以及iis创建站点。 3、本地的VS2022的安装目录:C:\Program Files\Microsoft Visual Studio\2022\Professional\Common7\IDE下找Remote Debugger 你的服务器是64位就拷贝x64的目…...

Java spring boot 一次调用多个请求
Java Spring Boot是一种基于Java编程语言的开发框架,它提供了一种快速构建高效、可伸缩和易于维护的企业级应用程序的方式。在实际的应用开发中,我们常常需要调用多个独立的请求来完成某个业务功能。然而,传统的同步方式一次只能调用一个请求…...
)
DRM全解析 —— CRTC详解(4)
接前一篇文章:DRM全解析 —— CRTC详解(3) 本文继续对DRM中CRTC的核心结构struct drm_crtc的成员进行释义。 3. drm_crtc结构释义 (21)struct drm_object_properties properties /** properties: property tracking …...

六个为Rust构建的IDE
Rust语言的学习曲线适中,介于高级语言和低级语言之间。这门语言既能编写系统软件,将嵌入式设备编译为x86 ARM,也可以用于前端技术,这要归功于WebAssembly。 在日渐成熟的发展中,Rust开始拥有更好的工具来提高效率。最…...

25 Python的collections模块
概述 在上一节,我们介绍了Python的sqlite3模块,包括:sqlite3模块中一些常用的函数和类。在这一节,我们将介绍Python的collections模块。collections模块是Python中的内置模块,它实现了特殊的容器数据类型,提…...

JEPG Encoder IP verilog设计及实现
总体介绍: 采用通用的常规 Verilog 代码编写,可用于任何 FPGA。 该内核不依赖任何专有 IP 内核,而是用 Verilog 编写了实现 JPEG 编码器所需的所有功能,代码完全独立。 编码器内核的输入是一条 24 位数据总线,红色像素、绿色像素和蓝色像素各有 8 位。 信号 "data_i…...
yolov5 web端部署进行图片和视频检测
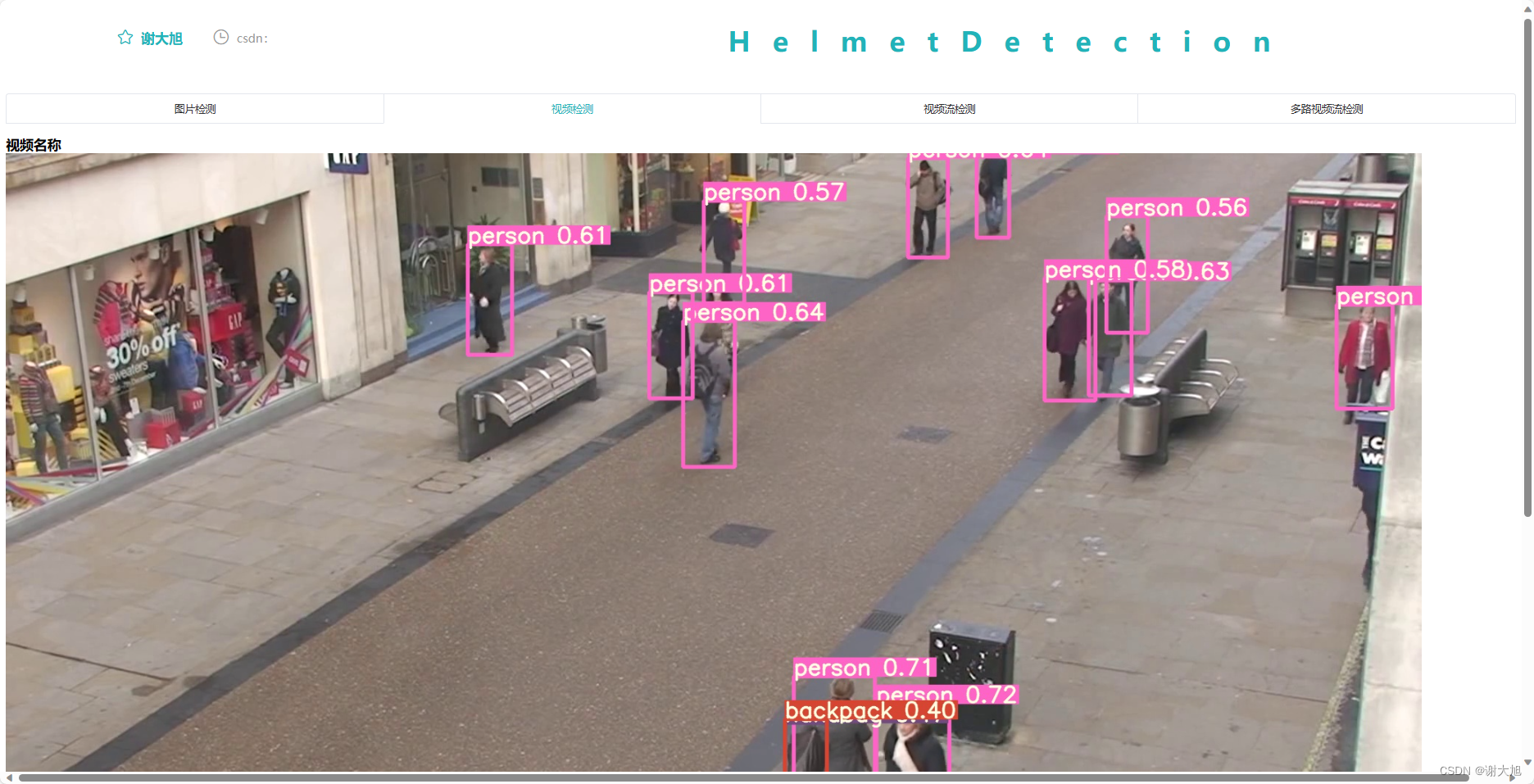
目录 1、思路 2、代码结构 3、代码运行 4、api接口代码 5、web ui界面 6、参考资料 7、代码分享 1、思路 通过搭建flask微型服务器后端,以后通过vue搭建网页前端。flask是第一个第三方库。与其他模块一样,安装时可以直接使用python的pip命令实现…...
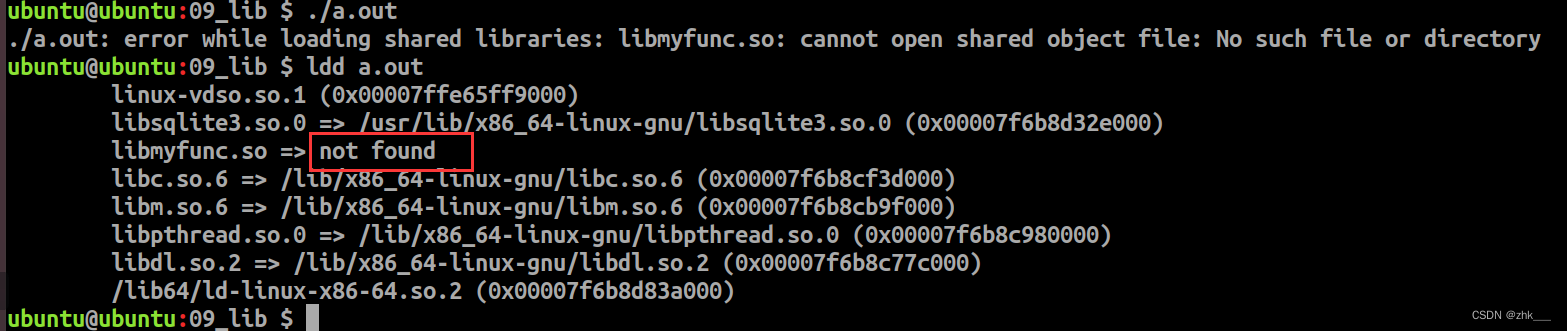
嵌入式养成计划-34--函数库
七十二、 函数库 1. 库的概念 库是一个二进制可执行文件,与二进制可执行程序比较,库是不能单独运行的。 库中存放的是功能函数,没有主函数(main函数) 库需要被载入到内存中使用 标准的基础库中存放了很多已经写好的…...

PM864AK01-eA 3BSE018161R2 工业人工智能供应链先驱
PM864AK01-eA 3BSE018161R2 工业人工智能供应链先驱 吞吐量和Macnica Networks的战略合作伙伴关系将使Macnica Networks的客户能够加速和量化智能工厂计划的投资回报(ROI)。高管、经理和运营负责人可以使用Macnica Networks领先的制造场所数据收集平台和ThroughPut基于约束理论…...

参与现场问题解决总结(Kafka、Hbase)
一. 背景 Kafka和Hbase在现场应用广泛,现场问题也较多,本季度通过对现场问题就行跟踪和总结,同时结合一些调研,尝试提高难点问题的解决效率,从而提高客户和现场满意度。非难点问题(历史遇到过问题…...
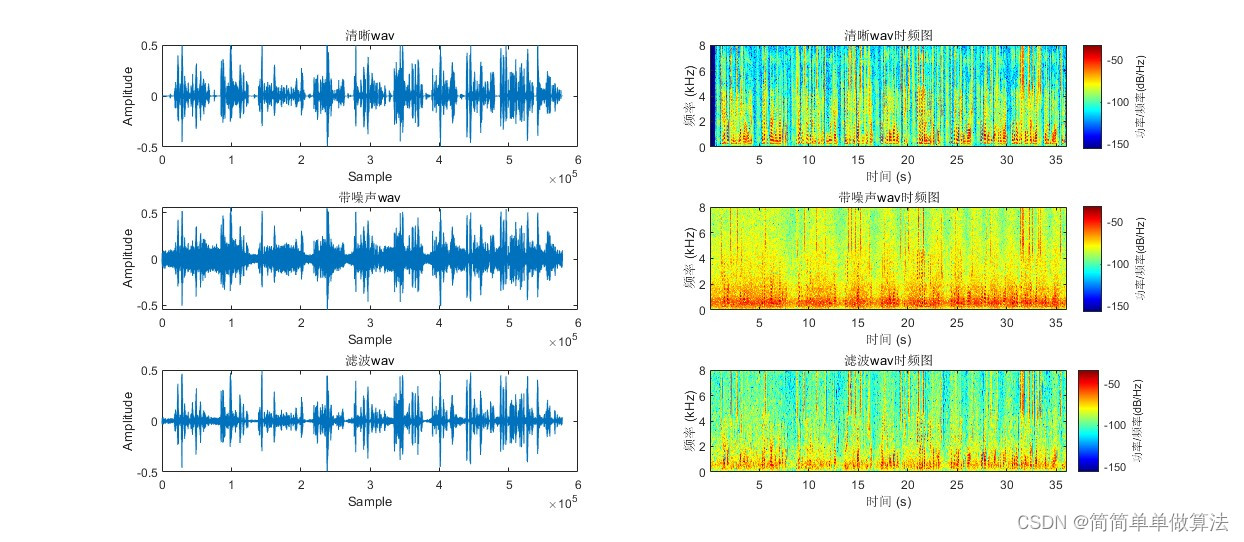
基于PSD-ML算法的语音增强算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 1.加窗处理: 2.分帧处理: 3.功率谱密度估计: 4.滤波处理: 5.逆变换处理: 6.合并处理: 5.算法完整程序工程 1.算法…...
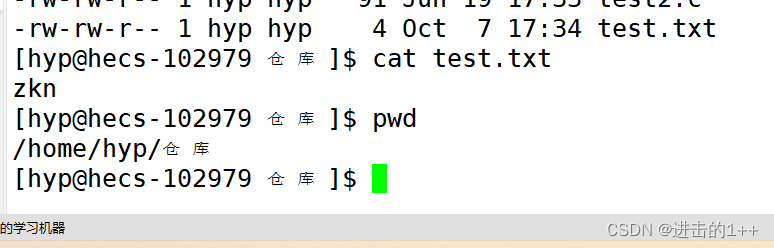
【1++的Linux】之文件(一)
👍作者主页:进击的1 🤩 专栏链接:【1的Linux】 文章目录 一,初识文件二,文件接口 一,初识文件 文件就是文件内容属性。因此对文件的操作无非就是对文件内容的操作和对文件属性的操作。 我们访问…...
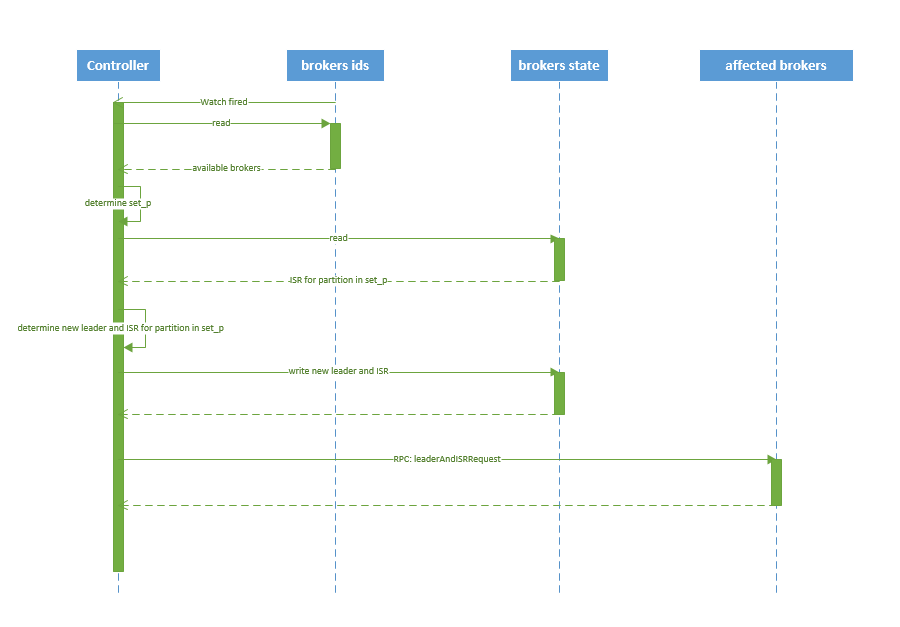
Kafka 高可用
正文 一、高可用的由来 1.1 为何需要Replication 在Kafka在0.8以前的版本中,是没有Replication的,一旦某一个Broker宕机,则其上所有的Partition数据都不可被消费,这与Kafka数据持久性及Delivery Guarantee的设计目标相悖。同时Pr…...
关于分布式操作系统
关于分布式操作系统,如果你不太理解的话,可以把它看成是传统操作系统延展。二者的区别在于,传统的操作系统都是单机系统,只能在一台计算机上运行,而分布式操作系统是多机系统,每台计算机都是系统中的一个计…...

Pytorch使用DataLoader, num_workers!=0时的内存泄露
描述一下背景,和遇到的问题: 我在做一个超大数据集的多分类,设备Ubuntu 22.04i9 13900KNvidia 409064GB RAM,第一次的训练的训练集有700万张,训练成功。后面收集到更多数据集,数据增强后达到了1000万张。…...
chromedriver下载与安装方法
下载与安装: 1.查看Chrome浏览器版本 首先,需要检查Chrome浏览器的版本。请按照以下步骤进行: 打开Chrome浏览器。 点击浏览器右上角的菜单图标(三个垂直点)。 选择“帮助”(Help)。 在下拉菜单中选择“…...
数据库查询详解
数据库查询操作 前置:首先我们创建一个练习的数据库 /* SQLyog Professional v12.09 (64 bit) MySQL - 5.6.40-log : Database - studentsys ********************************************************************* *//*!40101 SET NAMES utf8 */;/*!40101 SET …...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
