LeetCode 面试题 17.10. Find Majority Element LCCI【摩尔投票法】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
数组中占比超过一半的元素称之为主要元素。给你一个 整数 数组,找出其中的主要元素。若没有,返回 -1 。请设计时间复杂度为 O(N) 、空间复杂度为 O(1) 的解决方案。
示例 1:
输入:[1,2,5,9,5,9,5,5,5]
输出:5
示例 2:
输入:[3,2]
输出:-1
示例 3:
输入:[2,2,1,1,1,2,2]
输出:2
题目集合:
- 169. 多数元素
- 面试题 17.10. Find Majority Element LCCI
- 229. 多数元素 II
-
- Check If a Number Is Majority Element in a Sorted Array
- 1157. 子数组中占绝大多数的元素:困难
解法 Boyer-Moore 投票算法
由于题目要求时间复杂度 O ( n ) O(n) O(n) 和空间复杂度 O ( 1 ) O(1) O(1) ,因此符合要求的解法只有 Boyer-Moore 投票算法。这一投票算法在求出现次数大于 ⌊ n / 2 ⌋ \lfloor n / 2 \rfloor ⌊n/2⌋ 的元素 x x x 时很好理解:如果我们把 x x x 记为 + 1 +1 +1 ,把其他数记为 − 1 -1 −1 ,将它们全部加起来,显然和大于 0 0 0 ,从结果本身我们可以看出 x x x 比其他数多。
我们首先给出 Boyer-Moore 算法的详细步骤:
- 维护一个候选主要元素 c a n d i d a t e candidate candidate 和候选主要元素的出现次数 c o u n t count count ,初始时 c a n d i d a t e candidate candidate 为任意值, c o u n t = 0 count=0 count=0 ;
- 遍历数组 nums \textit{nums} nums 中的所有元素,遍历到元素 x x x 时,在判断 x x x 之前,如果 c o u n t = 0 count=0 count=0 ,我们先将 x x x 的值赋给 c a n d i d a t e candidate candidate ,否则不更新 c a n d i d a t e candidate candidate 的值。随后我们判断 x x x :
- 如果 x = c a n d i d a t e x=candidate x=candidate ,则将 c o u n t count count 加 1 1 1 ;
- 如果 x ≠ c a n d i d a t e x\ne candidate x=candidate ,则将 c o u n t count count 减 1 1 1 。
- 遍历结束之后,如果数组 n u m s nums nums 中存在主要元素,则 c a n d i d a t e candidate candidate 即为主要元素,否则 c a n d i d a t e candidate candidate 可能为数组中的任意一个元素。
- 由于不一定存在主要元素,因此需要第二次遍历数组,验证 c a n d i d a t e candidate candidate 是否为主要元素。第二次遍历时,统计 c a n d i d a t e candidate candidate 在数组中的出现次数,如果出现次数大于数组长度的一半,则 c a n d i d a t e candidate candidate 是主要元素,返回 c a n d i d a t e candidate candidate ,否则数组中不存在主要元素,返回 − 1 -1 −1 。
举一个具体的例子,例如下面的这个数组:
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
在遍历到数组中的第一个元素以及每个在 | 之后的元素时, c a n d i d a t e candidate candidate 都会因为 c o u n t count count 的值变为 0 0 0 而发生改变。最后一次 c a n d i d a t e candidate candidate 的值从 5 5 5 变为 7 7 7 ,也就是这个数组中的主要元素。
Boyer-Moore 算法的正确性较难证明,这里给出一种较为详细的用例子辅助证明的思路,供参考:
1.首先根据算法步骤中对 c o u n t count count 的定义,可以发现:在对整个数组进行遍历的过程中, c o u n t count count 的值一定非负。这是因为==如果 c o u n t count count 的值为 0 0 0 ,那么在这一轮遍历的开始时刻,我们会将 x x x 的值赋予 c a n d i d a t e candidate candidate 并在接下来的一步中将 c o u n t count count 的值增加 1 1 1 ==。因此 c o u n t count count 的值在遍历过程中一直保持非负。
2.那么 c o u n t count count 本身除了计数器之外,还有什么更深层次的意义呢?我们还是以数组:
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
作为例子,首先写下它在每一步遍历时 c a n d i d a t e candidate candidate 和 c o u n t count count 的值:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
candidate: 7 7 7 7 7 7 5 5 5 5 5 5 7 7 7 7
count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
我们再定义一个变量 v a l u e value value ,它和真正的主要元素 m a j maj maj 绑定。在每一步遍历时,如果当前的数 x x x 和 m a j maj maj 相等,那么 v a l u e value value 的值加 1 1 1 ,否则减 1 1 1 。 v a l u e value value 的实际意义即为:到当前的这一步遍历为止,主要元素出现的次数比非主要元素多出了多少次。我们将 v a l u e value value 的值也写在下方:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
value: 1 2 1 2 1 0 -1 0 -1 -2 -1 0 1 2 3 4
有没有发现什么?我们将 c o u n t count count 和 v a l u e value value 放在一起:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
value: 1 2 1 2 1 0 -1 0 -1 -2 -1 0 1 2 3 4
发现在每一步遍历中, c o u n t count count 和 v a l u e value value 要么相等,要么互为相反数!并且在候选主要元素 c a n d i d a t e candidate candidate 就是 m a j maj maj 时,它们相等, c a n d i d a t e candidate candidate 是其它的数时,它们互为相反数!
为什么会有这么奇妙的性质呢?这并不难证明:我们将候选主要元素 c a n d i d a t e candidate candidate 保持不变的连续的遍历称为「一段」。在同一段中, c o u n t count count 的值是根据 c a n d i d a t e = = x candidate == x candidate==x 的判断进行加减的。那么如果 c a n d i d a t e candidate candidate 恰好为 m a j maj maj ,那么在这一段中, c o u n t count count 和 v a l u e value value 的变化是同步的;如果 c a n d i d a t e candidate candidate 不为 m a j maj maj ,那么在这一段中 c o u n t count count 和 v a l u e value value 的变化是相反的。因此就有了这样一个奇妙的性质。
这样以来,由于:
- 我们证明了 c o u n t count count 的值一直为非负,在最后一步遍历结束后也是如此;
- 由于 v a l u e value value 的值与真正的主要元素 m a j maj maj 绑定,并且它表示「主要元素出现的次数比非主要元素多出了多少次」,那么在最后一步遍历结束后, v a l u e value value 的值为正数;
- 在最后一步遍历结束后, c o u n t count count 非负, v a l u e value value 为正数,所以它们不可能互为相反数,只可能相等,即 c o u n t = = v a l u e count == value count==value 。因此在最后「一段」中, c o u n t count count 的 v a l u e value value 的变化是同步的,也就是说, c a n d i d a t e candidate candidate 中存储的候选主要元素就是真正的主要元素 m a j maj maj 。
class Solution {
public:int majorityElement(vector<int>& nums) {int candidate = 0, count = 0;for (int num : nums) {if (count == 0) candidate = num;if (candidate == num) ++count;else --count;}count = 0;for (int num : nums) if (num == candidate) ++count;return count * 2 > nums.size() ? candidate : -1;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) ,其中 n n n 是数组 n u m s nums nums 的长度。
- 空间复杂度: O ( 1 ) O(1) O(1) 。只需要常数的额外空间。
相关文章:

LeetCode 面试题 17.10. Find Majority Element LCCI【摩尔投票法】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

多校联测11 模板题
题目大意 给你四个整数 n , m , s e e d , w n,m,seed,w n,m,seed,w,其中 n , m n,m n,m为两个多项式 A ( x ) ∑ i 0 n a i x i A(x)\sum\limits_{i0}^na_ix^i A(x)i0∑naixi和 B ( x ) ∑ i 0 m b i x i B(x)\sum\limits_{i0}^mb_ix^i B(x)i0∑mbixi…...
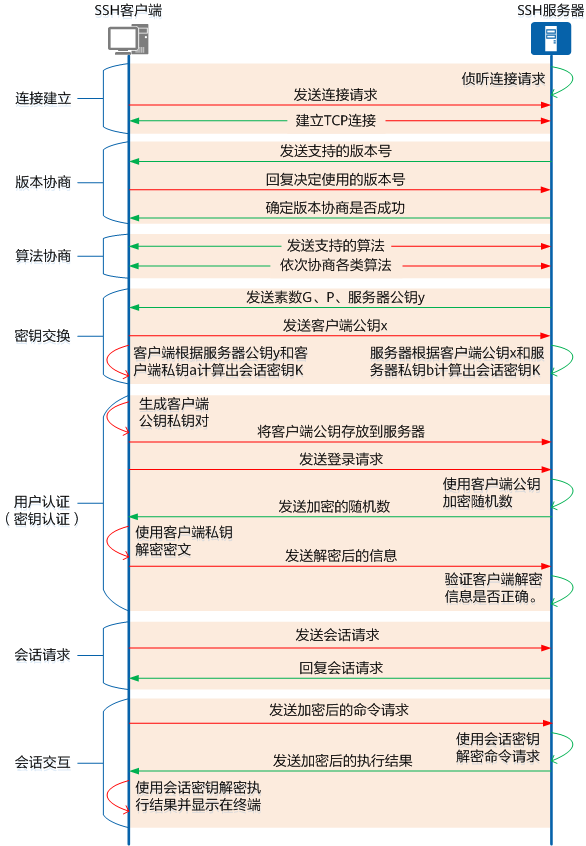
Linux SSH连接远程服务器(免密登录、scp和sftp传输文件)
1 SSH简介 SSH(Secure Shell,安全外壳)是一种网络安全协议,通过加密和认证机制实现安全的访问和文件传输等业务。传统远程登录和文件传输方式,例如Telnet、FTP,使用明文传输数据,存在很多的安全…...
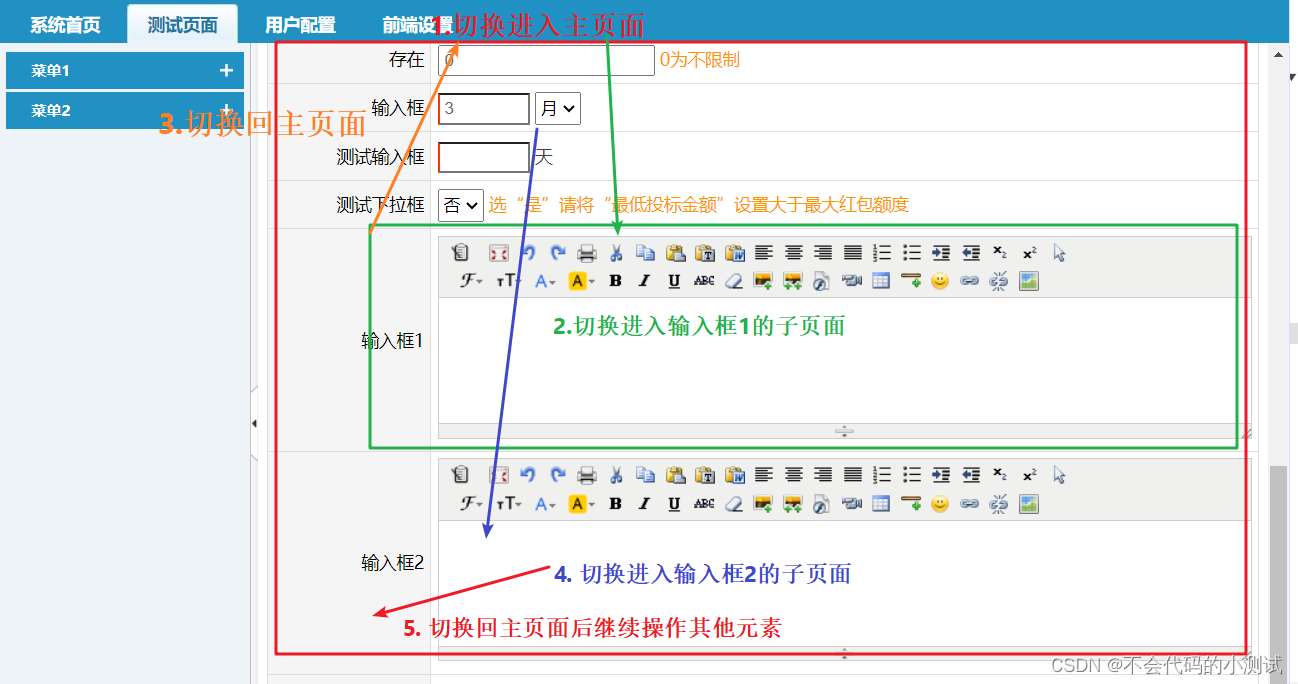
从0开始python学习-30.selenium frame子页面切换
目录 1. frame切换逻辑 2. 多层子页面情况进行切换 3. 多个子页面相互切换 1. frame切换逻辑 1.1. 子页面的类型一般分为两种 frame标签 iframe标签 1.2. 子页面里面的元素和主页面的元素是相互独立 子页面元素需要进去切换才能操作 如果已经进入子页面,那么…...
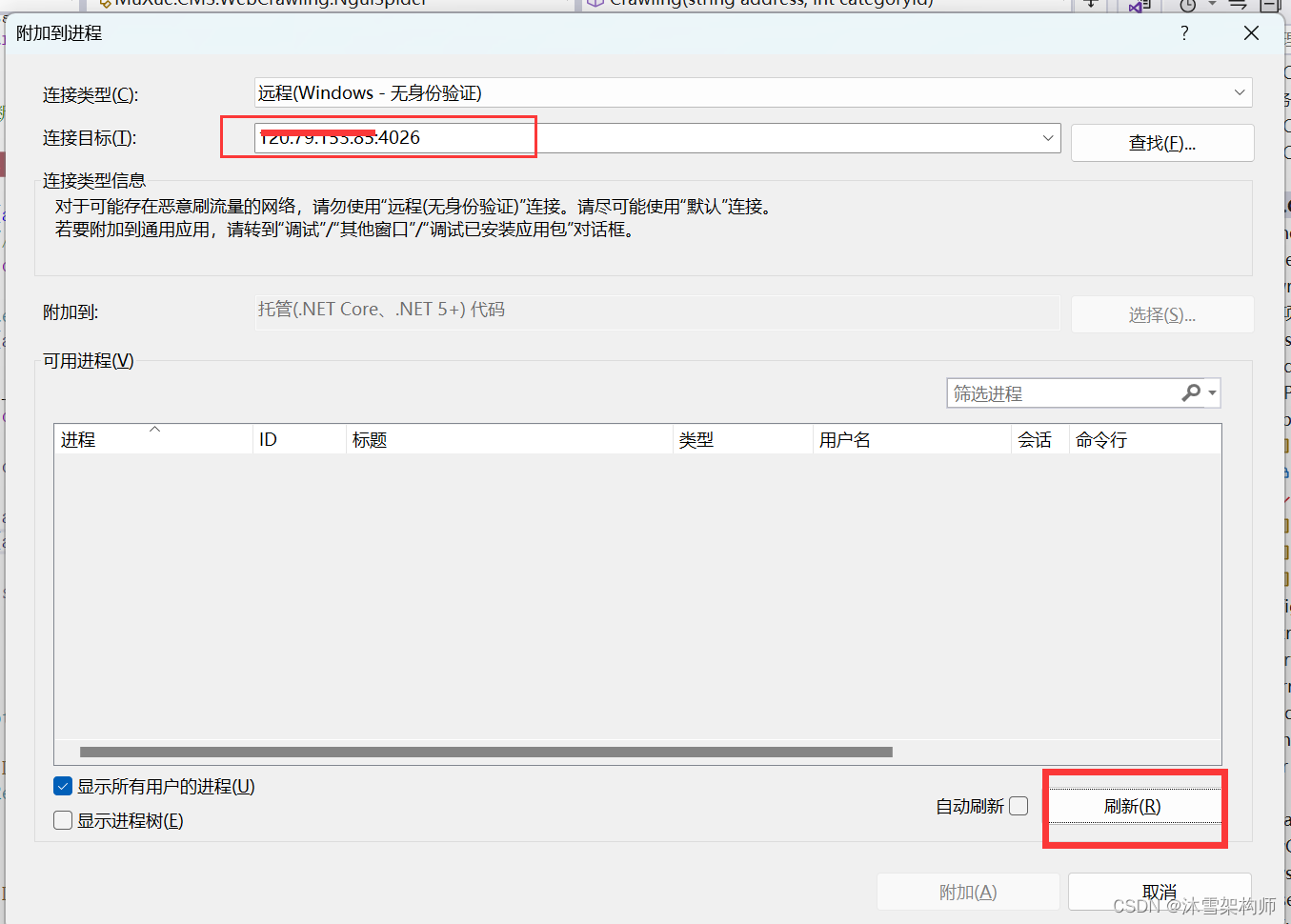
asp.net core 远程调试
大概说下过程: 1、站点发布使用Debug模式 2、拷贝到远程服务器,以及iis创建站点。 3、本地的VS2022的安装目录:C:\Program Files\Microsoft Visual Studio\2022\Professional\Common7\IDE下找Remote Debugger 你的服务器是64位就拷贝x64的目…...

Java spring boot 一次调用多个请求
Java Spring Boot是一种基于Java编程语言的开发框架,它提供了一种快速构建高效、可伸缩和易于维护的企业级应用程序的方式。在实际的应用开发中,我们常常需要调用多个独立的请求来完成某个业务功能。然而,传统的同步方式一次只能调用一个请求…...
)
DRM全解析 —— CRTC详解(4)
接前一篇文章:DRM全解析 —— CRTC详解(3) 本文继续对DRM中CRTC的核心结构struct drm_crtc的成员进行释义。 3. drm_crtc结构释义 (21)struct drm_object_properties properties /** properties: property tracking …...

六个为Rust构建的IDE
Rust语言的学习曲线适中,介于高级语言和低级语言之间。这门语言既能编写系统软件,将嵌入式设备编译为x86 ARM,也可以用于前端技术,这要归功于WebAssembly。 在日渐成熟的发展中,Rust开始拥有更好的工具来提高效率。最…...

25 Python的collections模块
概述 在上一节,我们介绍了Python的sqlite3模块,包括:sqlite3模块中一些常用的函数和类。在这一节,我们将介绍Python的collections模块。collections模块是Python中的内置模块,它实现了特殊的容器数据类型,提…...

JEPG Encoder IP verilog设计及实现
总体介绍: 采用通用的常规 Verilog 代码编写,可用于任何 FPGA。 该内核不依赖任何专有 IP 内核,而是用 Verilog 编写了实现 JPEG 编码器所需的所有功能,代码完全独立。 编码器内核的输入是一条 24 位数据总线,红色像素、绿色像素和蓝色像素各有 8 位。 信号 "data_i…...
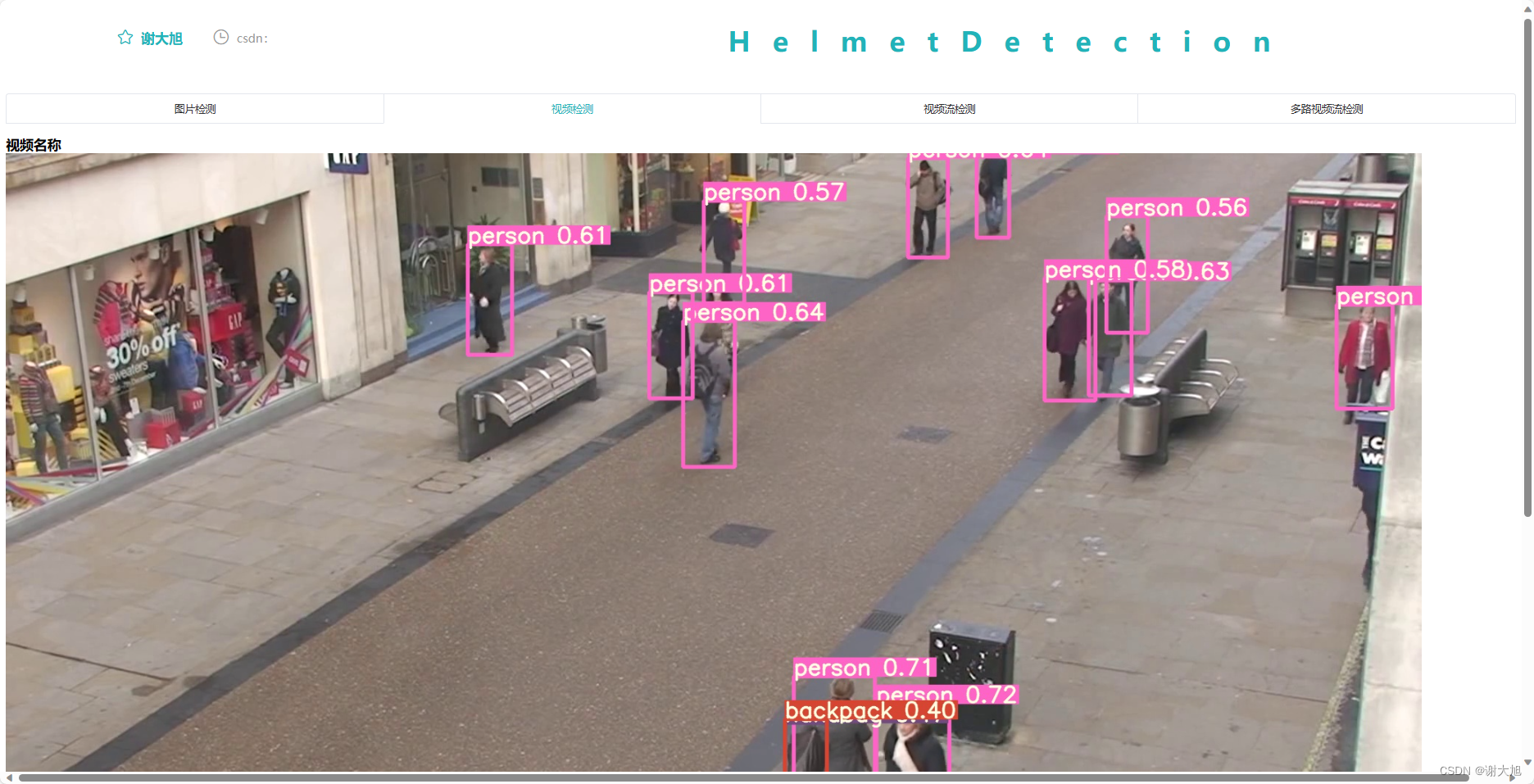
yolov5 web端部署进行图片和视频检测
目录 1、思路 2、代码结构 3、代码运行 4、api接口代码 5、web ui界面 6、参考资料 7、代码分享 1、思路 通过搭建flask微型服务器后端,以后通过vue搭建网页前端。flask是第一个第三方库。与其他模块一样,安装时可以直接使用python的pip命令实现…...
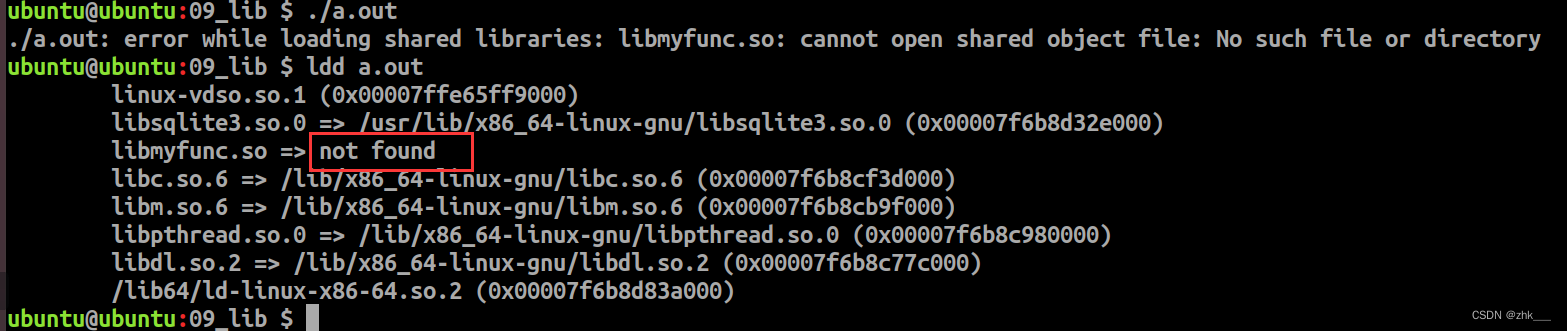
嵌入式养成计划-34--函数库
七十二、 函数库 1. 库的概念 库是一个二进制可执行文件,与二进制可执行程序比较,库是不能单独运行的。 库中存放的是功能函数,没有主函数(main函数) 库需要被载入到内存中使用 标准的基础库中存放了很多已经写好的…...

PM864AK01-eA 3BSE018161R2 工业人工智能供应链先驱
PM864AK01-eA 3BSE018161R2 工业人工智能供应链先驱 吞吐量和Macnica Networks的战略合作伙伴关系将使Macnica Networks的客户能够加速和量化智能工厂计划的投资回报(ROI)。高管、经理和运营负责人可以使用Macnica Networks领先的制造场所数据收集平台和ThroughPut基于约束理论…...

参与现场问题解决总结(Kafka、Hbase)
一. 背景 Kafka和Hbase在现场应用广泛,现场问题也较多,本季度通过对现场问题就行跟踪和总结,同时结合一些调研,尝试提高难点问题的解决效率,从而提高客户和现场满意度。非难点问题(历史遇到过问题…...
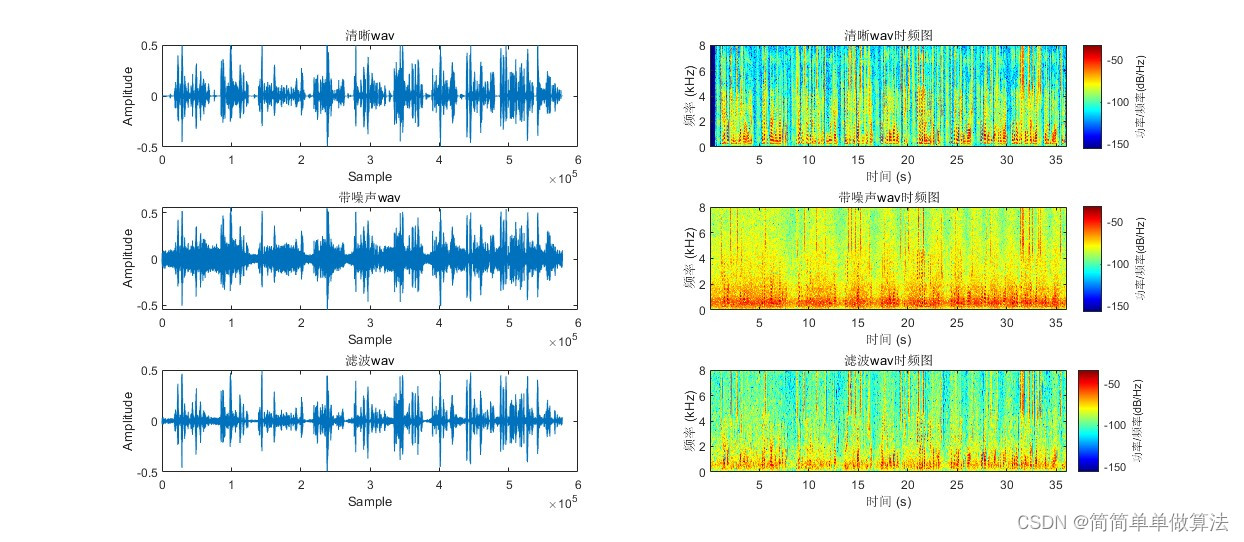
基于PSD-ML算法的语音增强算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 1.加窗处理: 2.分帧处理: 3.功率谱密度估计: 4.滤波处理: 5.逆变换处理: 6.合并处理: 5.算法完整程序工程 1.算法…...
【1++的Linux】之文件(一)
👍作者主页:进击的1 🤩 专栏链接:【1的Linux】 文章目录 一,初识文件二,文件接口 一,初识文件 文件就是文件内容属性。因此对文件的操作无非就是对文件内容的操作和对文件属性的操作。 我们访问…...
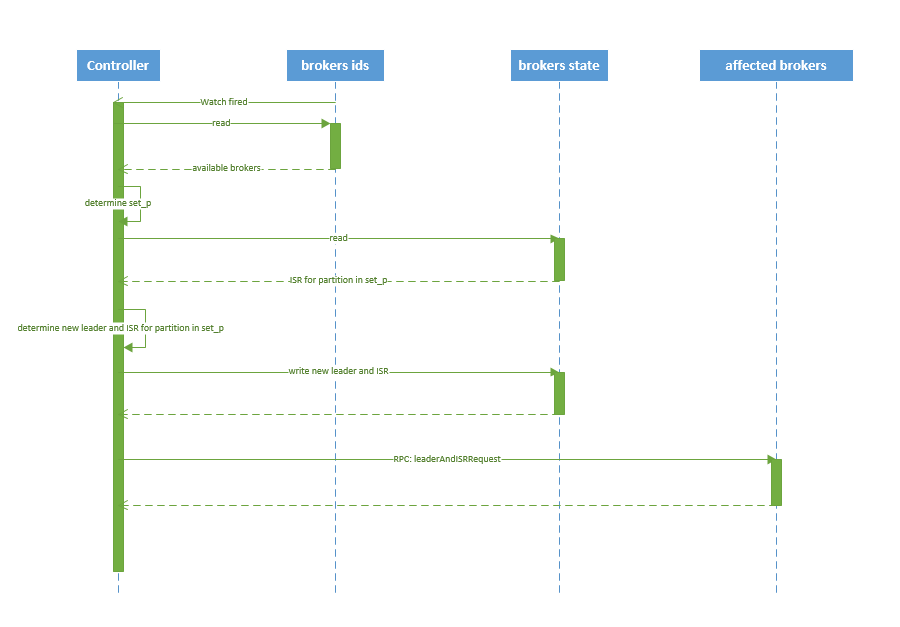
Kafka 高可用
正文 一、高可用的由来 1.1 为何需要Replication 在Kafka在0.8以前的版本中,是没有Replication的,一旦某一个Broker宕机,则其上所有的Partition数据都不可被消费,这与Kafka数据持久性及Delivery Guarantee的设计目标相悖。同时Pr…...
关于分布式操作系统
关于分布式操作系统,如果你不太理解的话,可以把它看成是传统操作系统延展。二者的区别在于,传统的操作系统都是单机系统,只能在一台计算机上运行,而分布式操作系统是多机系统,每台计算机都是系统中的一个计…...

Pytorch使用DataLoader, num_workers!=0时的内存泄露
描述一下背景,和遇到的问题: 我在做一个超大数据集的多分类,设备Ubuntu 22.04i9 13900KNvidia 409064GB RAM,第一次的训练的训练集有700万张,训练成功。后面收集到更多数据集,数据增强后达到了1000万张。…...
chromedriver下载与安装方法
下载与安装: 1.查看Chrome浏览器版本 首先,需要检查Chrome浏览器的版本。请按照以下步骤进行: 打开Chrome浏览器。 点击浏览器右上角的菜单图标(三个垂直点)。 选择“帮助”(Help)。 在下拉菜单中选择“…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
