大厂秋招真题【DP】米哈游20230924秋招T2-米小游与魔法少女-奇运
米哈游20230924秋招T2-米小游与魔法少女-奇运
题目描述与示例
题目描述
米小游都快保底了还没抽到希儿,好生气哦!只能打会活动再拿点水晶。
米小游和世界第一可爱的魔法少女 TeRiRi 正在打 BOSS,BOSS 的血量为h,当 BOSS 血量小于等于0时,BOSS 死亡。TeRiRi 有一套牌,在一轮中,她会按顺序一张一张的将卡牌打出,套牌中有两种卡牌:
- 时来运转:获得
x个幸运币。 - 幸运一掷:造成
x点伤害,并投掷所有幸运币,造成等于所有幸运币掷出的点数之和的伤害。
幸运币可以等概率的投掷出1∼6之间的点数。 (所以为什么不叫骰子呢?)
米小游想知道,TeRiRi 的套牌在一轮内击杀 BOSS 的概率。
输入描述
第一行输入两个整数n (1≤n≤100),h (1≤h≤10^9),分别表示卡牌张数和 BOSS 血量。
接下来n行,每行首先输入两个整数t (1≤t≤2),x (1≤x≤10),t为1表示卡牌为时来运转,t为2表示卡牌为幸运一掷。
输出描述
输出一个实数表示答案,你的答案与标准答案的误差不超过10^−4都被认为是正确答案。
示例一
输入
2 5
1 1
2 1
输出
0.5
说明
幸运币掷出4及以上的概率为0.5,再加上1点固定伤害,即可击杀BOSS。
示例二
输入
3 1145
1 4
1 9
1 9
输出
0
说明
无论如何都无法击杀BOSS。
解题思路
对于固定顺序的套牌,投掷幸运币的数量是固定的。这里要注意的是,由于时来运转之后必须接上幸运一掷才能将幸运币打出造成伤害,所以如果最后的若干张连续的卡牌是时来运转,这些最后获得的幸运币也是无法造成伤害的。
我们将造成的伤害分为两部分,固定伤害和随机伤害,前者为打出y个幸运币必定造成的z点伤害,后者为y个幸运币掷出点数和的伤害。
假设整套卡牌一共投掷了y个幸运币,造成的固定伤害为z点,如果想要击杀BOSS,随机伤害必须至少达到h-z点才可以。当然,如果h-z≤0,则必定可以击杀BOSS。
问题就转换为,投掷出y个幸运币,点数总和超过h-z的概率是多少?
由于每一个幸运币都是独立的,在掷出第i个幸运币时,其结果是从掷出第i-1个幸运币时得到的各种结果转移得到的,因此我们可以使用动态规划来解决该问题。我们考虑动态规划三部曲:
dp数组的含义是什么?
dp数组是一个长度为(y+1)×(h-z+1)的二维矩阵,dp[i][j]表示掷出第i个幸运币时,有多大的概率可以取得和为j的结果,即造成和为j的伤害。- 特别地,由于只需要判断伤害之和大于等于
h-z的概率,而不用关心具体的分布,dp数组内层的第h-z个元素,即dp[i][h-z],表示求和大于等于h-z的概率。
- 动态转移方程是什么?
- 由于幸运币掷出点数
1-6是等概率的,故对于某一个特定的dp[i-1][j],在掷出第i个幸运币时,dp[i-1][j]的结果将等概率地转换到dp[i][j+1],dp[i][j+2],dp[i][j+3],dp[i][j+4],dp[i][j+5],dp[i][j+6],即每一个状态都可以取得1/6的转移。 - 另外,如果
j+k之后超过了h-z,则将直接获得(7-k)/6 * dp[i-1][j]的概率。
for i in range(1, y+1):for j in range(i-1, h-z+1):for k in range(1, 7):if j + k >= h - z:dp[i][h-z] += (7-k)/6 * dp[i-1][j]breakelse:dp[i][j+k] += 1/6 * dp[i-1][j]
dp数组如何初始化?
- 考虑不投掷任何幸运币的情况,那么只有一种情况,也就是在投掷
0个幸运币的时候获得求和为0的概率为恒定1。故初始化dp[0][0] = 1
dp = [[0] * (h-z+1) for _ in range(y+1)]
dp[0][0] = 1
考虑完上述问题后,代码其实呼之欲出了。
代码
Python
# 题目:【DP】米哈游2023秋招-米小游与魔法少女-奇运
# 作者:闭着眼睛学数理化
# 算法:DP
# 代码有看不懂的地方请直接在群上提问y = 0 # 掷出幸运币的总个数
z = 0 # 全部造成的固定伤害
x_temp = 0 # 时来运转获得的幸运币n, h = map(int, input().split())
for _ in range(n):t, x = map(int, input().split())# 时来运转if t == 1:x_temp += x# 幸运一掷else:y += x_tempx_temp = 0z += x# 如果固定伤害已经大于h,直接输出1
if h - z <= 0:print(1)
# 否则才需要进行dp过程
else:# 初始化dp数组# dp[i][j]表示掷出了i个幸运币时,# 有多大的概率可以取得和为j的结果,即造成和为j的伤害。dp = [[0] * (h-z+1) for _ in range(y+1)]dp[0][0] = 1# 考虑每一个幸运币for i in range(1, y+1):# 对于每一个幸运币考虑打出i-1个硬币后的# 每一种求和结果的概率# 注意,由于已经掷出了i-1个幸运币# 那么求和结果至少为i-1,因为每个幸运币点数至少为1点# 因此j遍历时起点可以从i-1开始for j in range(i-1, h-z+1):# 如果求和j尚未在上一次投掷中取得,# 则可以直接考虑下一个幸运币if dp[i-1][j] == 0:break# 遍历掷出六种不同点数k的情况,# 当前点数则可以取得j+kfor k in range(1, 7):# 如果当前点数j+k超过了击杀所需点数# 则更新dp[i][h-z]# 为dp[i-1][j]对应的概率乘以(7-k)/6if j + k >= h - z:dp[i][h-z] += (7-k)/6 * dp[i-1][j]break# 如果当前点数j+k尚未超过击杀所需点数# 则其概率由dp[i-1][j]六等分后转移得到else:dp[i][j+k] += 1/6 * dp[i-1][j]# 输出最后一行的最后一个元素# 表示打出第y个幸运币后,造成伤害大于等于h-z点的概率print(dp[y][h-z])
Java
import java.util.Scanner;public class Main {public static void main(String[] args) {int y = 0; // 掷出幸运币的总个数int z = 0; // 全部造成的固定伤害int x_temp = 0; // 时来运转获得的幸运币Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int h = scanner.nextInt();for (int i = 0; i < n; i++) {int t = scanner.nextInt();int x = scanner.nextInt();// 时来运转if (t == 1) {x_temp += x;}// 幸运一掷else {y += x_temp;x_temp = 0;z += x;}}// 如果固定伤害已经大于h,直接输出1if (h - z < 0) {System.out.println("1");}// 否则才需要进行dp过程else {// 初始化dp数组// dp[i][j]表示掷出了i个幸运币时,// 有多大的概率可以取得和为j的结果,即造成和为j的伤害。double[][] dp = new double[y + 1][h - z + 1];dp[0][0] = 1.0;// 考虑每一个幸运币for (int i = 1; i <= y; i++) {// 对于每一个幸运币考虑打出i-1个硬币后的// 每一种求和结果的概率// 注意,由于已经掷出了i-1个幸运币// 那么求和结果至少为i-1,因为每个幸运币点数至少为1点// 因此j遍历时起点可以从i-1开始for (int j = i - 1; j <= h - z; j++) {// 如果求和j尚未在上一次投掷中取得,// 则可以直接考虑下一个幸运币if (dp[i - 1][j] == 0) {break;}// 遍历掷出六种不同点数k的情况,// 当前点数则可以取得j+kfor (int k = 1; k <= 6; k++) {// 如果当前点数j+k超过了击杀所需点数// 则更新dp[i][h-z]// 为dp[i-1][j]对应的概率乘以(7-k)/6if (j + k >= h - z) {dp[i][h - z] += (7 - k) / 6.0 * dp[i - 1][j];break;}// 如果当前点数j+k尚未超过击杀所需点数// 则其概率由dp[i-1][j]六等分后转移得到else {dp[i][j + k] += 1.0 / 6.0 * dp[i - 1][j];}}}}// 输出最后一行的最后一个元素// 表示打出第n个幸运币后,造成伤害大于等于h-z点的概率System.out.println(String.format("%.5f", dp[y][h - z]));}}
}
C++
#include <iostream>
#include <vector>
#include <iomanip>using namespace std;int main() {int y = 0; // 掷出幸运币的总个数int z = 0; // 全部造成的固定伤害int x_temp = 0; // 时来运转获得的幸运币int n, h;cin >> n >> h;for (int i = 0; i < n; i++) {int t, x;cin >> t >> x;// 时来运转if (t == 1) {x_temp += x;}// 幸运一掷else {y += x_temp;x_temp = 0;z += x;}}// 如果固定伤害已经大于h,直接输出1if (h - z < 0) {cout << fixed << setprecision(10) << 1 << endl;}// 否则才需要进行dp过程else {// 初始化dp数组// dp[i][j]表示掷出了i个幸运币时,// 有多大的概率可以取得和为j的结果,即造成和为j的伤害。vector<vector<double>> dp(y + 1, vector<double>(h - z + 1, 0));dp[0][0] = 1.0;// 考虑每一个幸运币for (int i = 1; i <= y; i++) {// 对于每一个幸运币考虑打出i-1个硬币后的// 每一种求和结果的概率// 注意,由于已经掷出了i-1个幸运币// 那么求和结果至少为i-1,因为每个幸运币点数至少为1点// 因此j遍历时起点可以从i-1开始for (int j = i - 1; j <= h - z; j++) {// 如果求和j尚未在上一次投掷中取得,// 则可以直接考虑下一个幸运币if (dp[i - 1][j] == 0) {break;}// 遍历掷出六种不同点数k的情况,// 当前点数则可以取得j+kfor (int k = 1; k <= 6; k++) {// 如果当前点数j+k超过了击杀所需点数// 则更新dp[i][h-z]// 为dp[i-1][j]对应的概率乘以(7-k)/6if (j + k >= h - z) {dp[i][h - z] += (7 - k) / 6.0 * dp[i - 1][j];break;}// 如果当前点数j+k尚未超过击杀所需点数// 则其概率由dp[i-1][j]六等分后转移得到else {dp[i][j + k] += 1.0 / 6.0 * dp[i - 1][j];}}}}// 输出最后一行的最后一个元素// 表示打出第n个幸运币后,造成伤害大于等于h-z点的概率cout << fixed << setprecision(5) << dp[y][h - z] << endl;}return 0;
}
时空复杂度
时间复杂度:O(yh)。其中y为投掷出的幸运币的总数,h为BOSS总血量,dp过程需要进行双重循环。
空间复杂度:O(yh)。dp数组所占空间。如果使用滚动dp,空间复杂度可以降低到O(h)
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务100+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 OD算法冲刺训练课程表 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多
相关文章:

大厂秋招真题【DP】米哈游20230924秋招T2-米小游与魔法少女-奇运
米哈游20230924秋招T2-米小游与魔法少女-奇运 题目描述与示例 题目描述 米小游都快保底了还没抽到希儿,好生气哦!只能打会活动再拿点水晶。 米小游和世界第一可爱的魔法少女 TeRiRi 正在打 BOSS,BOSS 的血量为h,当 BOSS 血量小…...
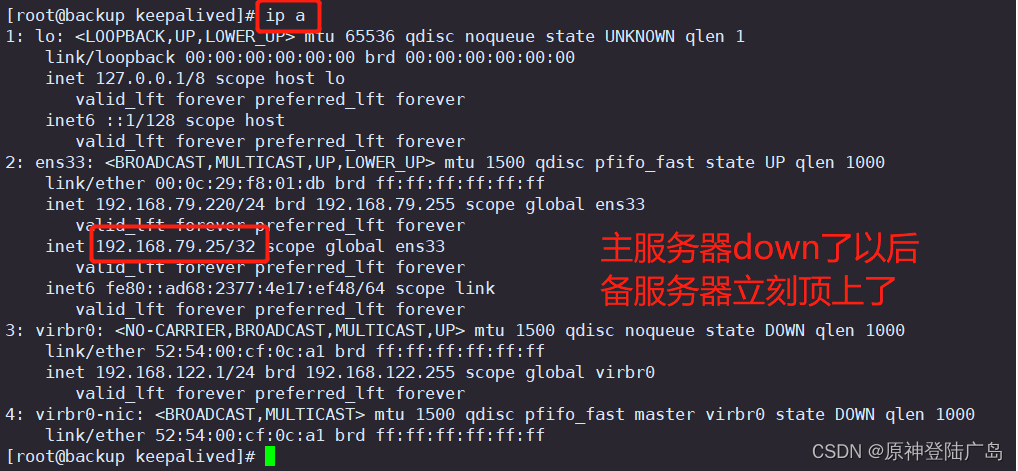
LVS+Keepalived 高可用集群负载均衡
一.keepalived介绍 1.1.Keepalived实现原理 由多台路由器组成一个热备组,通过共用的虚拟IP地址对外提供服务。 每个热备组内同时只有一台主路由器提供服务,其他路由器处于冗余状态。 若当前在线的路由器失效,则其他路由器会根据设置…...

Qt QList类和QLinkedList类 详解
一、QList 类 对于不同的数据类型,QList<T>采取不同的存储策略,存储策略如下: 如果T 是一个指针类型或指针大小的基本类型(该基本类型占有的字节数和指针类型占有的字节数相同),QList<T>将数值直接存储在它的数组当…...

Mac安装GYM遇到的一些坑
以下是遇到的一些问题 安装GitHub上说的直接 pip install gym成功了,但是运行实例报错没安装gym[classic_control],所以就全安装一下[all] 安装GitHub上说的直接 pip install gym成功了,但是运行实例报错没安装gym[classic_control]ÿ…...
【高级rabbitmq】
文章目录 1. 消息丢失问题1.1 发送者消息丢失1.2 MQ消息丢失1.3 消费者消息丢失1.3.1 消费失败重试机制 总结 2. 死信交换机2.1 TTL 3. 惰性队列3.1 总结: 4. MQ集群 消息队列在使用过程中,面临着很多实际问题需要思考: 1. 消息丢失问题 1.1…...
数百个下载能够传播 Rootkit 的恶意 NPM 软件包
供应链安全公司 ReversingLabs 警告称,最近观察到的一次恶意活动依靠拼写错误来诱骗用户下载恶意 NPM 软件包,该软件包会通过 rootkit 感染他们的系统。 该恶意软件包名为“node-hide-console-windows”,旨在模仿 NPM 存储库上合法的“node-…...

SpringBoot的error用全局异常去处理
记录一下使用SpringBoot2.0.5的error用全局异常去处理 在使用springboot时,当访问的http地址或者说是请求地址输错后,会返回一个页面,如下: 这是因为请求的地址不存在,默认会显示error页面 但我们实际需要一个接口&a…...
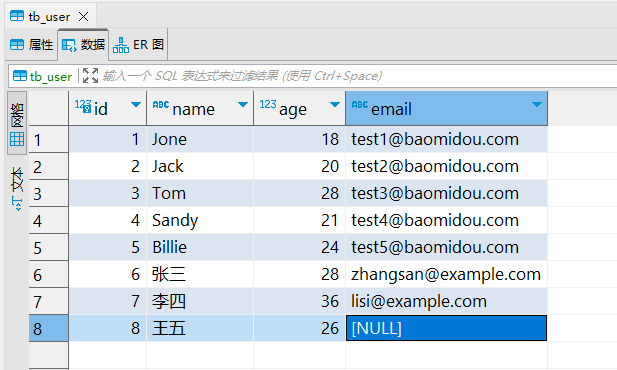
MyBatisPlus(十一)包含查询:in
说明 包含查询,对应SQL语句中的 in 语句,查询参数包含在入参列表之内的数据。 in Testvoid inNonEmptyList() {// 非空列表,作为参数List<Integer> ages Stream.of(18, 20, 22).collect(Collectors.toList());in(ages);}Testvoid in…...

Linux命令定位与查找:which、whereis和find的用法详解
文章目录 Linux命令的定位与查找1. 简介Linux路径环境变量命令行和Shell 2. which命令which命令的作用使用which命令定位可执行文件多个可执行文件的定位which命令的选项及其使用 3. whereis命令whereis命令的作用使用whereis命令查找二进制文件查找源代码文件whereis命令的选项…...

LeetCode 面试题 17.10. Find Majority Element LCCI【摩尔投票法】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

多校联测11 模板题
题目大意 给你四个整数 n , m , s e e d , w n,m,seed,w n,m,seed,w,其中 n , m n,m n,m为两个多项式 A ( x ) ∑ i 0 n a i x i A(x)\sum\limits_{i0}^na_ix^i A(x)i0∑naixi和 B ( x ) ∑ i 0 m b i x i B(x)\sum\limits_{i0}^mb_ix^i B(x)i0∑mbixi…...
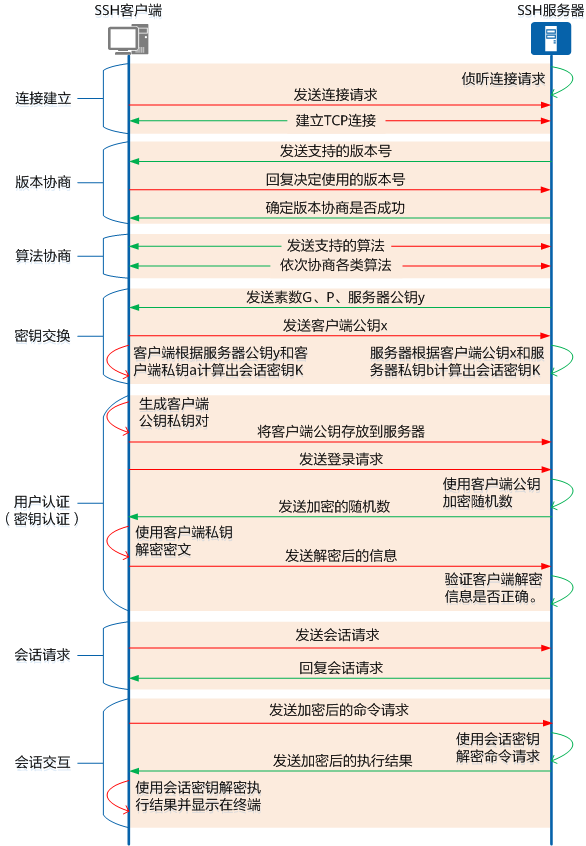
Linux SSH连接远程服务器(免密登录、scp和sftp传输文件)
1 SSH简介 SSH(Secure Shell,安全外壳)是一种网络安全协议,通过加密和认证机制实现安全的访问和文件传输等业务。传统远程登录和文件传输方式,例如Telnet、FTP,使用明文传输数据,存在很多的安全…...
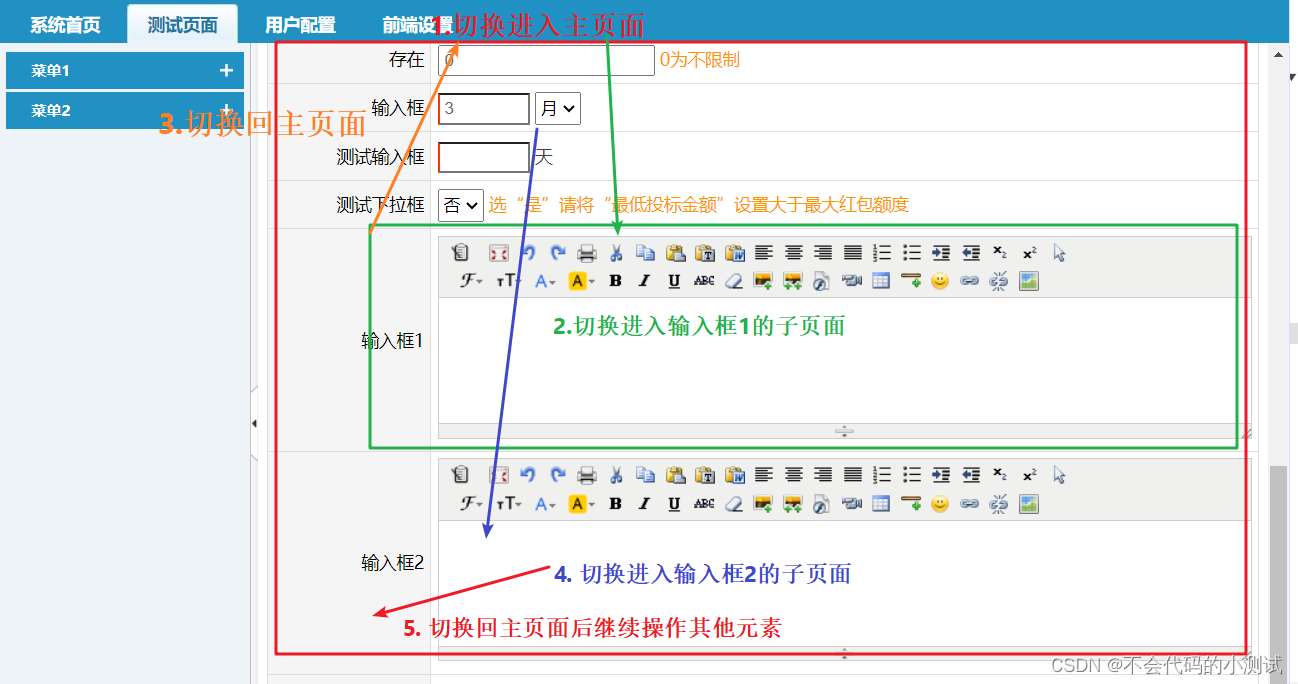
从0开始python学习-30.selenium frame子页面切换
目录 1. frame切换逻辑 2. 多层子页面情况进行切换 3. 多个子页面相互切换 1. frame切换逻辑 1.1. 子页面的类型一般分为两种 frame标签 iframe标签 1.2. 子页面里面的元素和主页面的元素是相互独立 子页面元素需要进去切换才能操作 如果已经进入子页面,那么…...
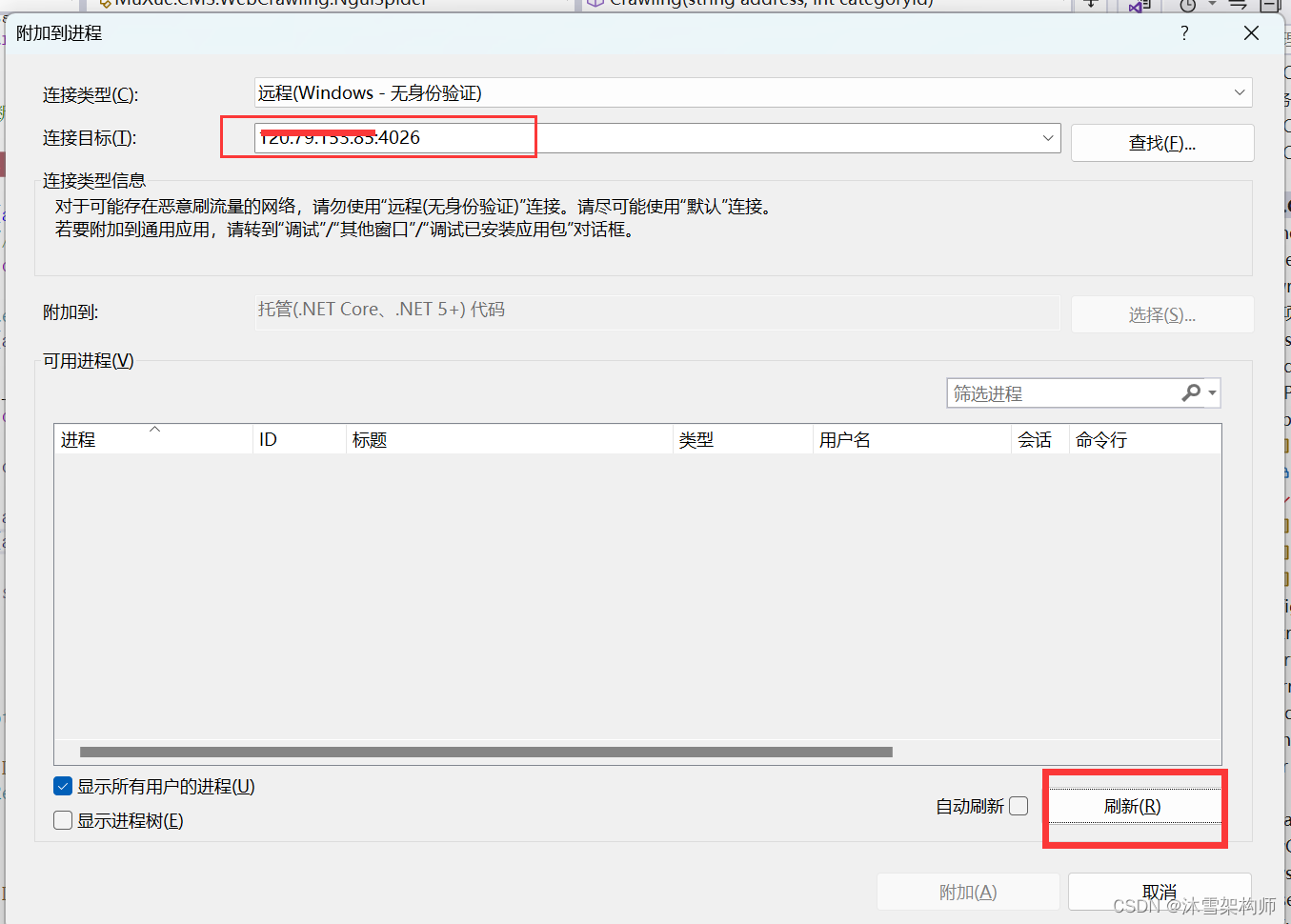
asp.net core 远程调试
大概说下过程: 1、站点发布使用Debug模式 2、拷贝到远程服务器,以及iis创建站点。 3、本地的VS2022的安装目录:C:\Program Files\Microsoft Visual Studio\2022\Professional\Common7\IDE下找Remote Debugger 你的服务器是64位就拷贝x64的目…...

Java spring boot 一次调用多个请求
Java Spring Boot是一种基于Java编程语言的开发框架,它提供了一种快速构建高效、可伸缩和易于维护的企业级应用程序的方式。在实际的应用开发中,我们常常需要调用多个独立的请求来完成某个业务功能。然而,传统的同步方式一次只能调用一个请求…...
)
DRM全解析 —— CRTC详解(4)
接前一篇文章:DRM全解析 —— CRTC详解(3) 本文继续对DRM中CRTC的核心结构struct drm_crtc的成员进行释义。 3. drm_crtc结构释义 (21)struct drm_object_properties properties /** properties: property tracking …...

六个为Rust构建的IDE
Rust语言的学习曲线适中,介于高级语言和低级语言之间。这门语言既能编写系统软件,将嵌入式设备编译为x86 ARM,也可以用于前端技术,这要归功于WebAssembly。 在日渐成熟的发展中,Rust开始拥有更好的工具来提高效率。最…...

25 Python的collections模块
概述 在上一节,我们介绍了Python的sqlite3模块,包括:sqlite3模块中一些常用的函数和类。在这一节,我们将介绍Python的collections模块。collections模块是Python中的内置模块,它实现了特殊的容器数据类型,提…...

JEPG Encoder IP verilog设计及实现
总体介绍: 采用通用的常规 Verilog 代码编写,可用于任何 FPGA。 该内核不依赖任何专有 IP 内核,而是用 Verilog 编写了实现 JPEG 编码器所需的所有功能,代码完全独立。 编码器内核的输入是一条 24 位数据总线,红色像素、绿色像素和蓝色像素各有 8 位。 信号 "data_i…...
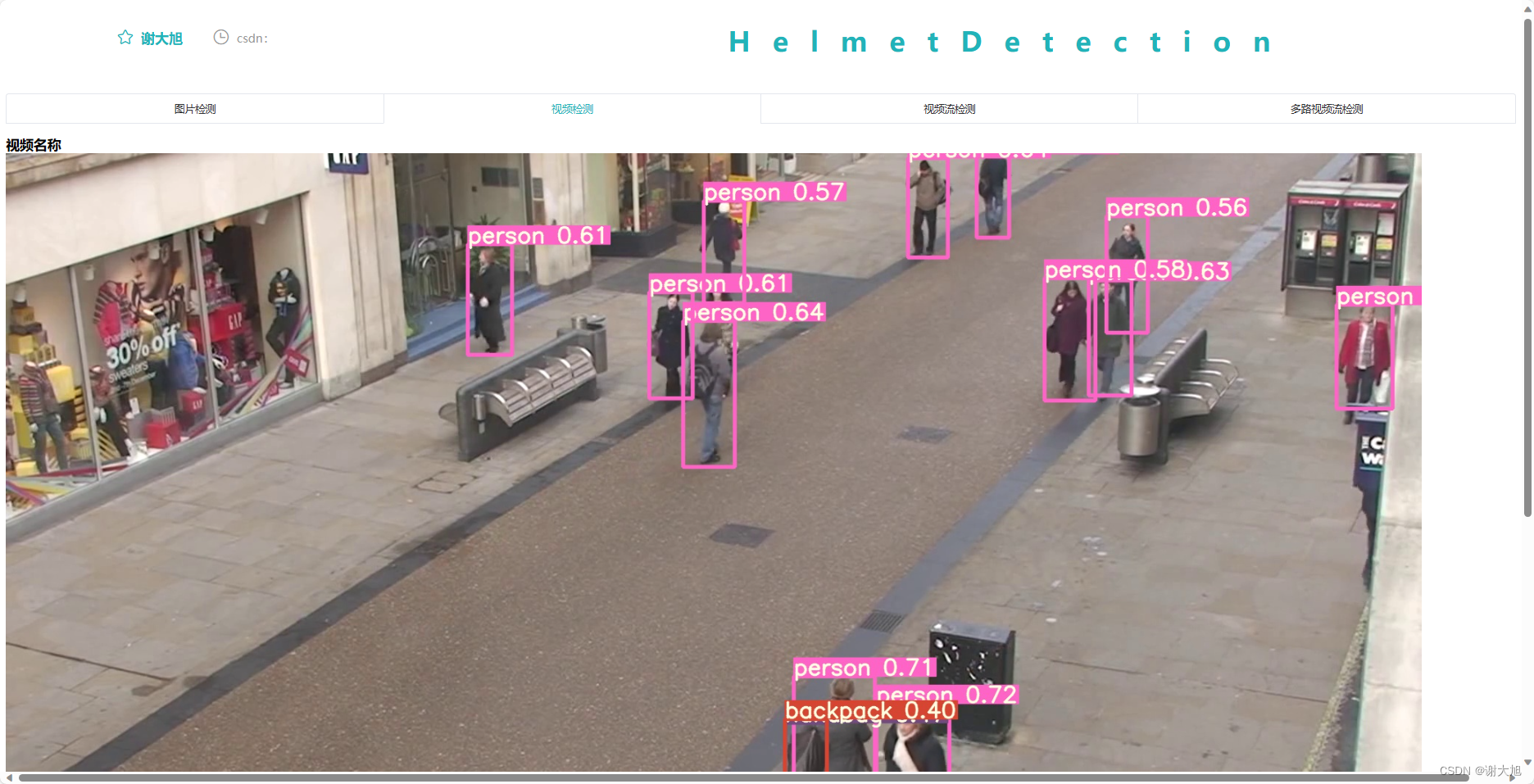
yolov5 web端部署进行图片和视频检测
目录 1、思路 2、代码结构 3、代码运行 4、api接口代码 5、web ui界面 6、参考资料 7、代码分享 1、思路 通过搭建flask微型服务器后端,以后通过vue搭建网页前端。flask是第一个第三方库。与其他模块一样,安装时可以直接使用python的pip命令实现…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
