李沐深度学习记录2:10多层感知机
一.简要知识记录
x.numel():看向量或矩阵里元素个数
A.sum():向量或矩阵求和,axis参数可对某维度求和,keepdims参数设置是否保持维度不变
A.cumsum:axis参数设置沿某一维度计算矩阵累计和x*y:向量的按元素乘法
torch.dot(x,y):向量的点乘(点积or内积),结果是标量。公式,向量a点积向量b=|a||b|cos两向量夹角。向量点积即x的转置与向量y相乘,即对应元素相乘相加得数值。
torch.sum(x*y):计算向量点积的另一方式,执行向量的按元素乘法得向量,再对向量求和。torch.mul(A,x):两个变量对应元素相乘。A为矩阵时,x可以是一个数,也可以是向量(支持广播机制)。若A(m,n),x为向量时,x只能(1,n)或(m,1)即选择与矩阵A每行向量对应元素想乘或者与矩阵A每列向量对应元素想乘,显然(n,1)或(1,m)维度不符合形式。
torch.mv(A,X):矩阵向量积,矩阵乘以向量。A*B:矩阵的按元素乘法,称为Hadamard积。
torch.mm(A,B):矩阵乘法。但是注意,高维矩阵(二维以上)不可以使用mm(),应当使用matmul().torch.abs(x).sum():计算向量的L1范数,即先计算各项绝对值,再求和。
torch.norm(x):计算向量的L2范数。L2范数是向量元素平方和的平方根
torch.norm(A):类似于向量的L2范数,矩阵A的Frobenius范数是矩阵元素平方和的平方根。梯度和等高线正交,梯度指向值变化最大的方向1.线性回归:估计一个连续值
公式(对于单个样本,向量内积),y=<w,x>+b (<w,x>向量内积得标量) ;
公式(对于多个样本,矩阵乘法),y=w*x+b x维度[batchsize,m], w维度[m,1], b维度[1]是个标量,输出维度[batchsize,1]
损失函数,平方损失 ;
输出:输出只有一个连续值表预测 2.softmax回归:预测一个离散类别;设类别数n
公式(对多个样本):1)y=w*x+b;x维度[batchsize,m], w维度[m,n] ,b维度[1,n], 输出维度[batchsize,n]2)y=softmax(o);o是1)的输出值,通过softmax将其转化为概率输出,即n个值和为1
损失函数;交叉熵( H(p,q)=求和-pi*log(qi) )常用于衡量两个概率的区别,一个是正确类别进行的一位有效编码,一个是2)的预测概率输出
输出:输出n个类别的概率预测
另,逻辑斯蒂回归是softmax回归二分类的一种特殊形式3.单层感知机:二分类
公式(对于单个样本):o=硬sigmoid(<w,x>+b) 硬sigmoid(x)=1(x>0) or -1(otherwise)
损失函数:等价于使用批量大小为1的梯度下降,具体如下
l=max(0,-y<w,x>) 当预测值<w,x>与真实值y符号相同即均大于0或均小于0,该样本预测正确,此时-y<w,x>小于0,损失函数l=0当预测值<w,x>与真实值y符号不同,该样本预测错误,此时-y<w,x>大于0,损失函数l=-y<w,x>
存在问题,无法解决XOR二分类问题多层感知机-单分类即二分类
公式(对多个样本):h=sigmoid(w1*x+b1) 输入x维度(batchsize,n),隐藏层w1维度(n,m), b1维度(1,m), 隐藏层输出维度(batchsize,m)o=w2*h+b2 输入h维度(batchsize,m),输出层w2维度(m,1), b2维度(1)标量,输出o维度(batchsize,1)
关于激活函数:sigmoid:[0,1] Tanh: [-1,1] ReLU: max(x,0) 常用ReLU,因为它没有指数运算,而指数计算很贵多层感知机-多分类
公式(对多个样本):h=sigmoid(w1*x+b1) 输入x维度(batchsize,n),隐藏层w1维度(n,m), b1维度(1,m), 隐藏层输出维度(batchsize,m)o=w2*h+b2 输入h维度(batchsize,m),输出层w2维度(m,k), b2维度(k,1),输出o维度(batchsize,k) y=softmax(o) 通过softmax将k个值转化为概率
损失函数:交叉熵
超参数:隐藏层数;每个隐藏层的大小
另,多层感知机多分类与softmax回归多分类区别只是多了隐藏层部分
2.多层感知机从零开始实现
import torch
from torch import nn
from d2l import torch as d2l#数据加载
batch_size=256
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)实现一个具有单隐藏层的多层感知机
#初始化模型参数
#注意对于隐藏层的宽度,常选择2的若干次幂作为层的宽度,可以使得计算更高效
num_inputs,num_outputs,num_hiddens=784,10,256#nn.Parameter()是pytorch一个类,用于创建可训练的参数(权重和偏置),这些参数会在模型训练过程中自动更新
# w1=nn.Parameter(torch.normal(0,0.01,(num_inputs,num_hiddens),requires_grad=True)*0.01)
w1=nn.Parameter(torch.randn(num_inputs,num_hiddens,requires_grad=True)*0.01)
b1=nn.Parameter(torch.zeros(num_hiddens,requires_grad=True))
w2=nn.Parameter(torch.randn(num_hiddens,num_outputs,requires_grad=True)*0.01)
b2=nn.Parameter(torch.zeros(num_outputs,requires_grad=True))params=[w1,b1,w2,b2]#激活函数-实现ReLU函数
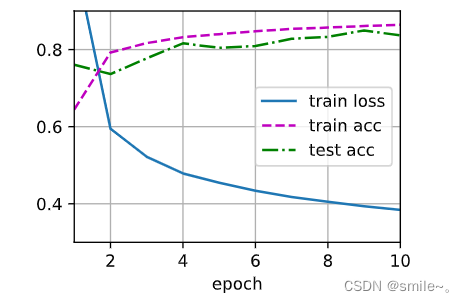
def relu(X):a=torch.zeros_like(X) #torch.zeros_like生成和括号内变量维度一致的全是0的内容return torch.max(X,a)#模型
#忽略空间结构,需要使用reshape将每个二维图像转换为一个长度为num_inputs的向量
def net(X):X=X.reshape((-1,num_inputs)) #(batchsize,1,28,28)->(batchsize,784)H=relu(X@w1+b1) #X矩阵(batchsize,784),w1矩阵(784,256),@则为矩阵乘法得(batchsize,256),b1(1,256)return (H@w2+b2) #H矩阵(batchsize,256),w1矩阵(256,10),@则为矩阵乘法得(batchsize,10),b2(1,10)#损失函数
#计算softmax和交叉熵
loss=nn.CrossEntropyLoss(reduction='none') #不对损失求和或求平均,得到一个向量包含batchsize份损失,即每个样本的损失#训练
#由于多层感知机训练过程与softmax回归完全相同,因此可以直接调用d2l包的train_ch3函数
num_epochs,lr=10,0.1
updater=torch.optim.SGD(params,lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,updater)#在一些数据上应用模型
d2l.predict_ch3(net,test_iter)

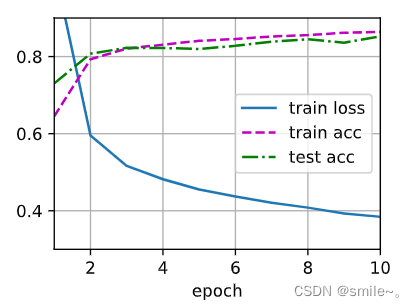
三.多层感知机简介实现
import torch
from torch import nn
from d2l import torch as d2l#加载数据
batch_size=256
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)#模型
#与softmax回归的简洁实现,唯一区别是添加了2个全连接层
#第一层隐藏层,包含256个隐藏单元,并使用ReLU激活函数。第二层是输出层
#nn.Flatten()除了第0维度batchsize保留,其余维度全部展平为一维向量
net=nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))
#参数初始化
#nn.Linear的weight和bias会自动初始化,这里使用init_weight只是不希望采用对weight的默认初始化,对bias采用默认初始化就可以
def init_weights(m):if type(m)==nn.Linear:nn.init.normal_(m.weight,std=0.01)net.apply(init_weights);#损失函数
loss=nn.CrossEntropyLoss(reduction='none')#优化算法
trainer=torch.optim.SGD(net.parameters(),lr=lr)#训练
num_epochs,lr=10,0.1
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
相关文章:

李沐深度学习记录2:10多层感知机
一.简要知识记录 x.numel():看向量或矩阵里元素个数 A.sum():向量或矩阵求和,axis参数可对某维度求和,keepdims参数设置是否保持维度不变 A.cumsum:axis参数设置沿某一维度计算矩阵累计和x*y:向量的按元素乘法 torch.…...

Python标准库中内置装饰器@staticmethod@classmethod
装饰器是Python中强大而灵活的功能,用于修改或增强函数或方法的行为。装饰器本质上是一个函数,它接受另一个函数作为参数,并返回一个新的函数,通常用于在不修改原始函数代码的情况下添加额外的功能或行为。这种技术称为元编程&…...
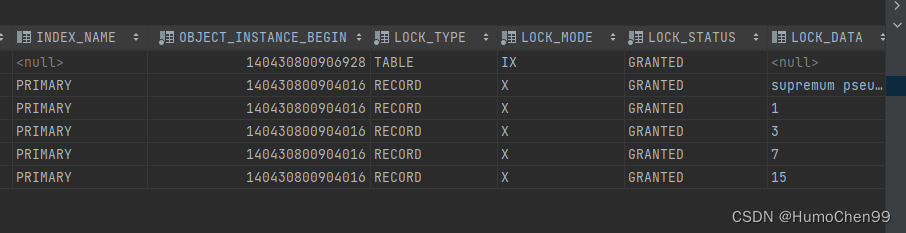
MySQL8 间隙锁在11种情况下的锁持有情况分析
测试环境及相关必要知识 测试环境为mysql 8 版本 间隙锁(Gap Lock):用于锁定索引范围之间的间隙,防止其他事务在此间隙中插入新记录。间隙锁主要用于防止幻读问题。 在可重复读的隔离级别下默认打开该锁机制,解决幻…...

C# 图片按比例进行压缩
1、对图片进行压缩,保存在本地 对于一个200k的png文件按0.6的缩放比例进行压缩,压缩后的大小为20k左右 对于一个80k的jpg文件按0.6的缩放比例压缩,压缩后为13k左右 public void imageZoom(string name, Double zoomScale){Bitmap btImage …...

猜猜 JavaScript 输出:(! + [] + [] + ![]).length
一起猜 最近看到一个很有意思的题,直接来看,下面这段代码的打印结果是什么? console.log((! [] [] ![]).length) 猜猜看,你的答案是什么,打在评论区。 我的答案是 undefined,正如我的英文名 为什么呢&a…...

MTK Android12静默安装接口
该文档就是在android12系统上提供一个广播接收器,app端发送一个广播,并且带入apk的地址就可以实现安装 1、广播注册 frameworks\base\services\core\java\com\android\server\policy\PhoneWindowManager.java 首先要导入的依赖 import android.app.P…...
基于电容电流前馈与电网电压全前馈的三相LCL并网逆变器谐波抑制Simulink仿真
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Python数据攻略-Pandas与统计数据分析
统计学在数据分析中到底有多重要?在数据分析的世界里,统计学扮演着一角色。想象一下你是《三国志》游戏的数据分析师,任务是找出哪个武将最受玩家欢迎,哪些战役最具挑战性等。 你怎么做呢?这就需要统计学的力量了。 文章目录 基础统计方法描述性统计方差和标准差相关性和…...
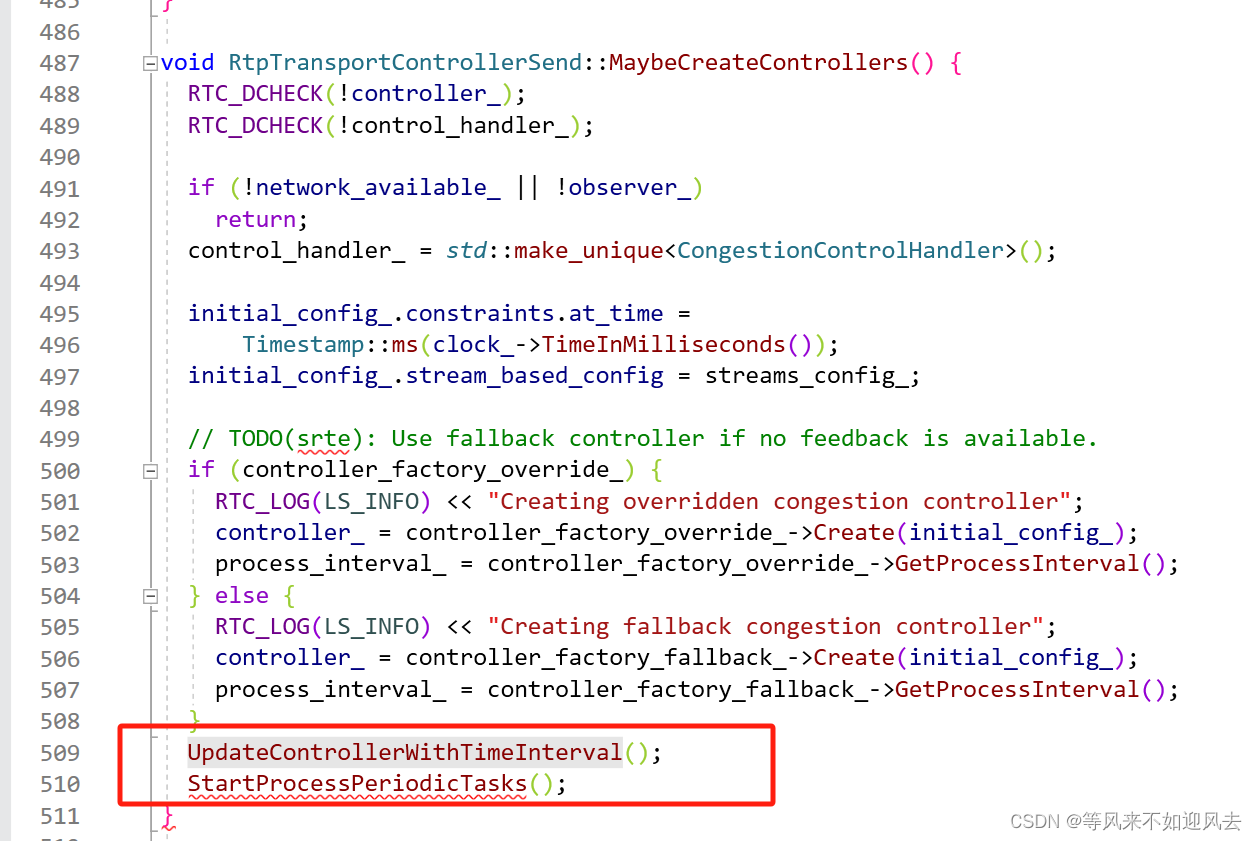
【gcc】RtpTransportControllerSend学习笔记 1
本文是大神 https://www.cnblogs.com/ishen 的文章的学习笔记。主要是大神文章: webrtc源码分析(8)-拥塞控制(上)-码率预估 的学习笔记。大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。因为直接看大神的文章,自己啥也没记住,所以同时跟着看代码。跟…...

若依分离版-前端使用
1 执行 npm install --registryhttps://registry.npm.taobao.org,报错信息如下 npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: ktg-mes-ui3.8.2 npm ERR! Found: vue2.6.12 npm ERR! node_modu…...

微信小程序-2
微信开发文档 https://developers.weixin.qq.com/miniprogram/dev/framework/ 一、app.js中的生命周期函数与globalData(全局变量) 指南 - - - 小程序框架 - - - 注册小程序 删除app.js里的东西,输入App回车,调用生命周期 选项 - - - 重新打开此项目…...
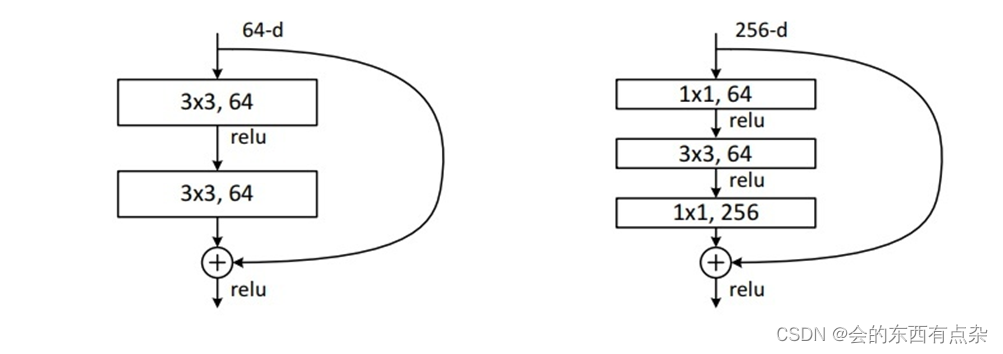
卷积神经网络的发展历史-ResNet
ResNet的产生 2015 年,Kaiming He 提出了ResNet(拿到了 2016 年 CVPR Best Paper Award),不仅解决了神经网络中的退化问题还在同年的ILSVRC和COCO 竞赛横扫竞争对手,分别拿下分类、定位、检测、分割任务的第一名。 R…...
基于瞬时无功功率ip-iq的谐波信号检测Simulink仿真
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

node安装,nvm管理器
一、下载nvm,nvm-setup.exe https://github.com/coreybutler/nvm-windows/releases 二、配置NodeJS下载代理镜像(可选) 可以在NVM安装根目录下的setting.txt文件中,配置NodeJS下载代理镜像,解决在线安装NodeJS时速度…...
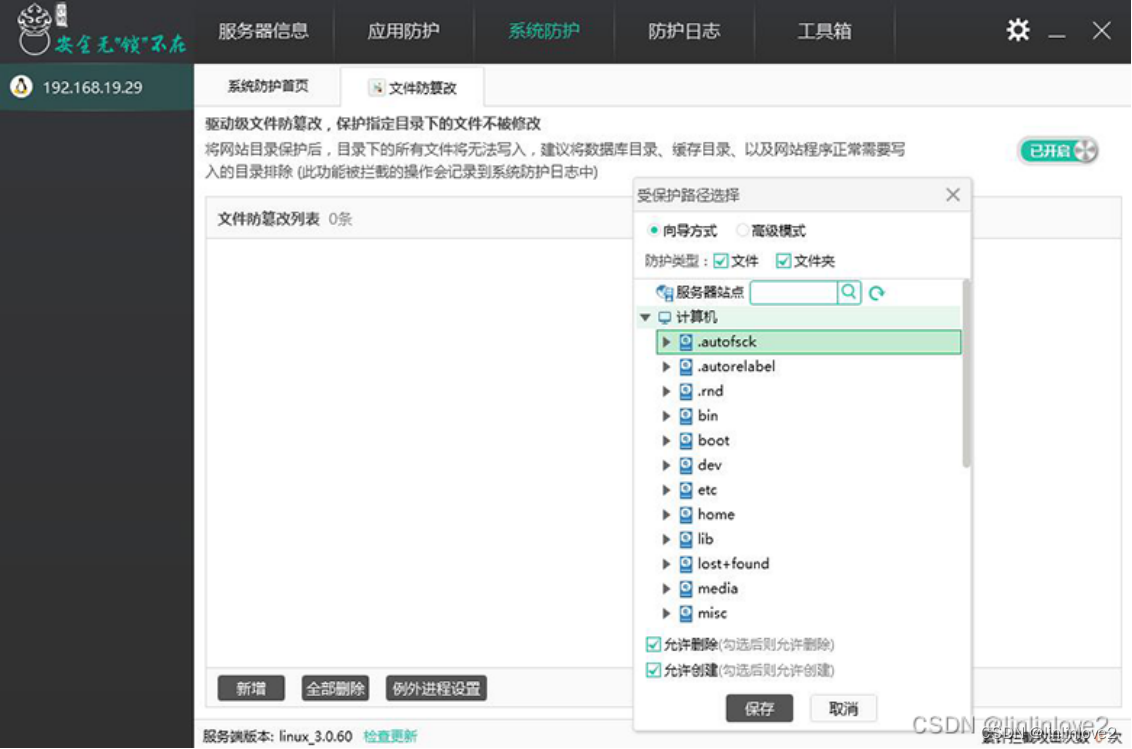
华为云云耀云服务器L实例评测|Ubuntu云锁防火墙安装搭建使用
华为云云耀云服务器L实例评测|Ubuntu安装云锁防火墙对抗服务器入侵和网络攻击 1.前言概述 华为云耀云服务器L实例是新一代开箱即用、面向中小企业和开发者打造的全新轻量应用云服务器。多种产品规格,满足您对成本、性能及技术创新的诉求。云耀云服务器L…...
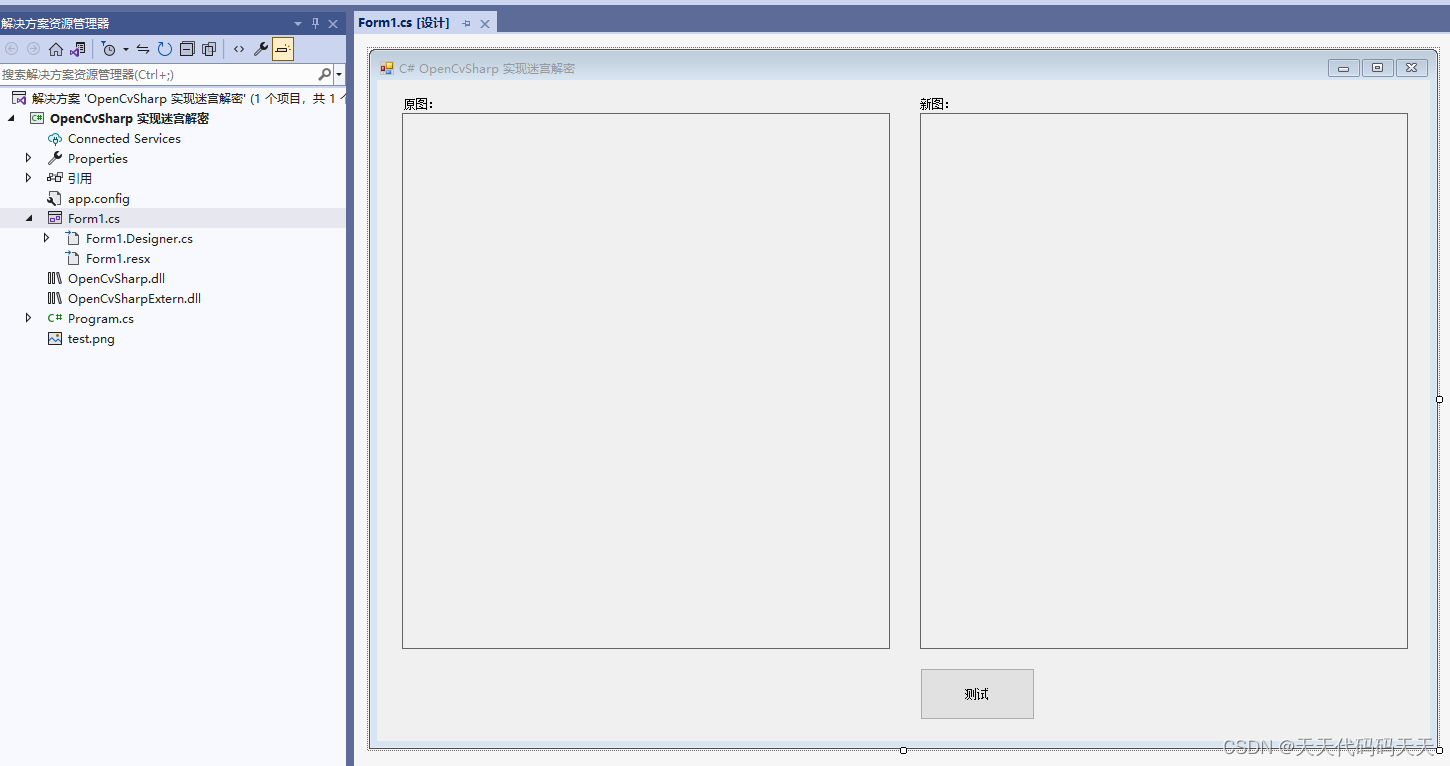
C# OpenCvSharp 实现迷宫解密
效果 项目 代码 using OpenCvSharp; using System; using System.Drawing; using System.Windows.Forms;namespace OpenCvSharp_实现迷宫解密 {public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e…...
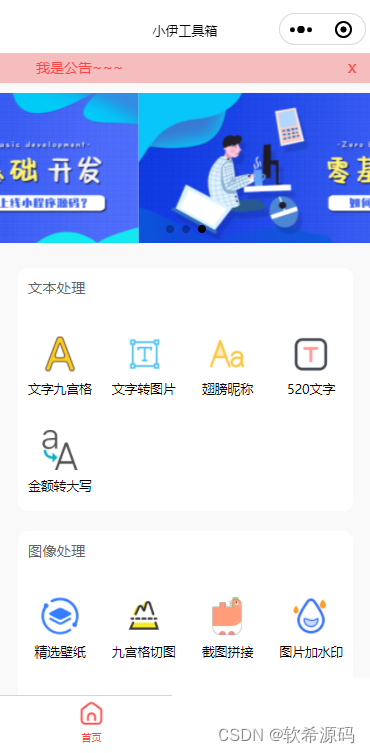
趣味工具箱小程序源码
趣味工具箱小程序源码,支持功能去水印,精选壁纸,图片压缩,文字生成二维码,图片加水印,模拟来电,手持弹幕,掷骰子…等 使用小工具,一个小程序有几十个功能。 源码下载&am…...

互联网Java工程师面试题·Redis 篇·第二弹
目录 16、Redis 集群方案什么情况下会导致整个集群不可用? 17、Redis 支持的 Java 客户端都有哪些?官方推荐用哪个? 18、Jedis 与 Redisson 对比有什么优缺点? 19、Redis 如何设置密码及验证密码? 20、说说 Redis…...
)
FreeRTOS入门教程(信号量的概念及API函数使用)
文章目录 前言一、什么是信号量二、信号量种类和对比三、信号量和队列的区别四、信号量相关的函数1.创建函数2.删除函数3.获取和释放信号量函数 总结 前言 本篇文章正式带大家开始学习什么是信号量,并且掌握信号量函数的基本使用方法,并且将和队列进行一…...
简易版Pycharm(2023)+Conda开发环境配置教程
困 扰 不知道为什么,自从Pycharm更新了新的版本以后,在Pycharm中为项目工程配置Python解释器环境时,总是不能像以前那么方便的配置。 比如,当前Conda中有十个不同的开发环境,每个环境一个名称,比如&#x…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
