斐波那契数列 JS
问题:
给出一个数字,找出它是斐波那契数列中的第几个数
斐波那契数列 [1, 1, 2, 3, 5, 8, 13, ...],后一个数字是前两个数字之和
输入的数字大于等于 2
如果输入数字不存于斐波那契数列中,返回 -1
function demo(num) {//初始数据const start = [1, 1]const res = DiGui(start, num)return res
}function DiGui(start, num) {const end = start[0] + start[1]if (end === num) {//找到了,输出return end} else if (end > num) {//不存在return -1} else if (end < num) {//继续找return DiGui([start[1], end], num)}
}console.log(demo(5))//5
console.log(demo(13))//13
console.log(demo(9))//-1
相关文章:

斐波那契数列 JS
问题: 给出一个数字,找出它是斐波那契数列中的第几个数 斐波那契数列 [1, 1, 2, 3, 5, 8, 13, ...],后一个数字是前两个数字之和 输入的数字大于等于 2 如果输入数字不存于斐波那契数列中,返回 -1 function demo(num) {//初始数据…...

IP 地址的分类
IP地址是用于标识计算机或设备在互联网上的位置的一种地址。IP地址通常根据其范围和用途分为不同的分类,主要包括以下几种: IPv4地址(Internet Protocol version 4): IPv4地址是32位二进制数,通常以点分十…...
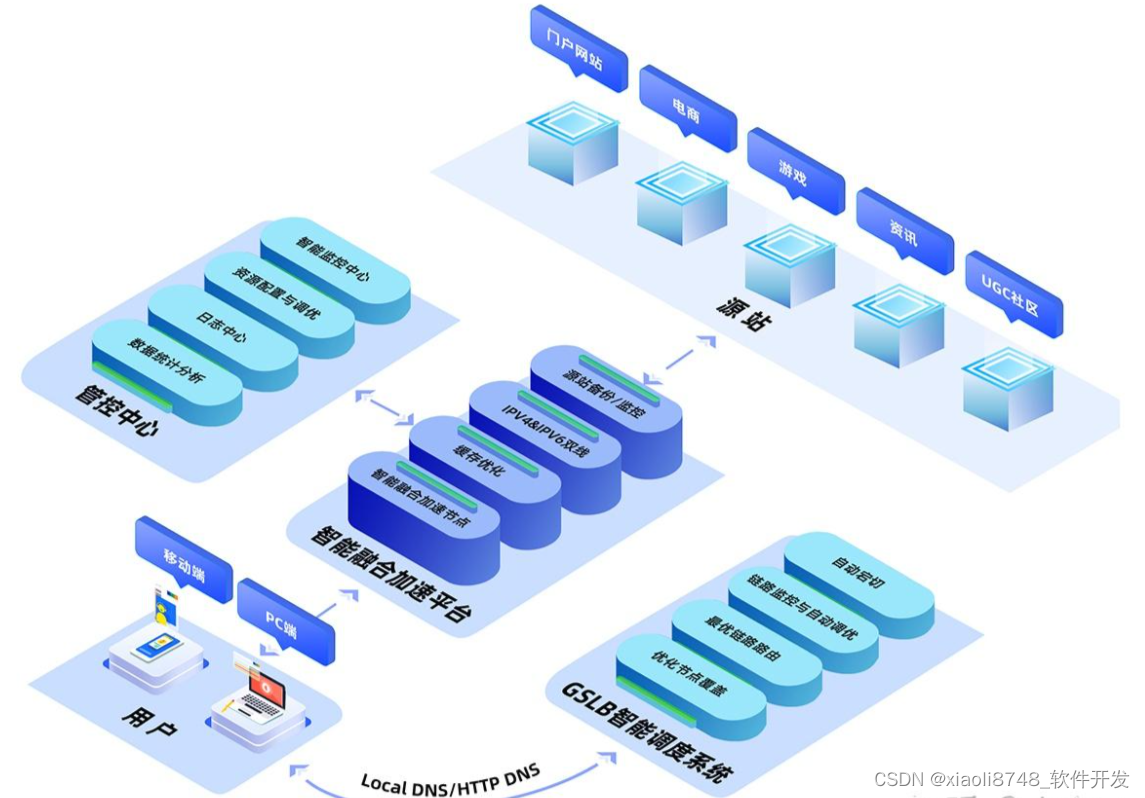
CDN网络基础入门:CDN原理及架构
背景 互联网业务的繁荣让各类门户网站、短视频、剧集观看、在线教育等内容生态快速发展,互联网流量呈现爆发式增长,自然也面临着海量内容分发效率上的挑战,那么作为终端用户,我们获取资源的体验是否有提升呢? 答案是…...
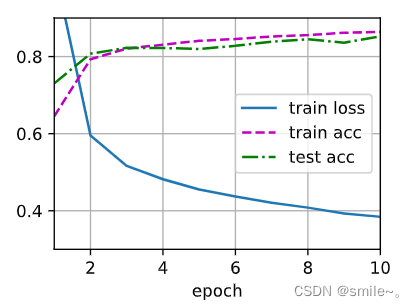
李沐深度学习记录2:10多层感知机
一.简要知识记录 x.numel():看向量或矩阵里元素个数 A.sum():向量或矩阵求和,axis参数可对某维度求和,keepdims参数设置是否保持维度不变 A.cumsum:axis参数设置沿某一维度计算矩阵累计和x*y:向量的按元素乘法 torch.…...

Python标准库中内置装饰器@staticmethod@classmethod
装饰器是Python中强大而灵活的功能,用于修改或增强函数或方法的行为。装饰器本质上是一个函数,它接受另一个函数作为参数,并返回一个新的函数,通常用于在不修改原始函数代码的情况下添加额外的功能或行为。这种技术称为元编程&…...
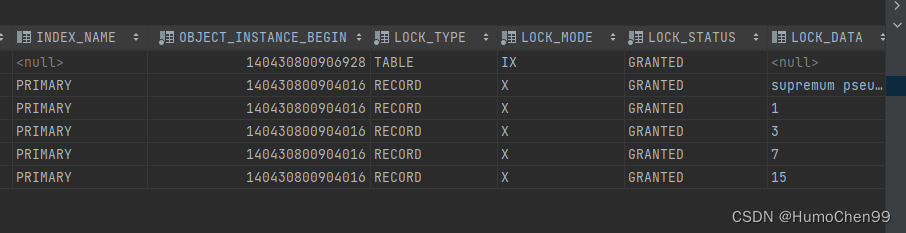
MySQL8 间隙锁在11种情况下的锁持有情况分析
测试环境及相关必要知识 测试环境为mysql 8 版本 间隙锁(Gap Lock):用于锁定索引范围之间的间隙,防止其他事务在此间隙中插入新记录。间隙锁主要用于防止幻读问题。 在可重复读的隔离级别下默认打开该锁机制,解决幻…...

C# 图片按比例进行压缩
1、对图片进行压缩,保存在本地 对于一个200k的png文件按0.6的缩放比例进行压缩,压缩后的大小为20k左右 对于一个80k的jpg文件按0.6的缩放比例压缩,压缩后为13k左右 public void imageZoom(string name, Double zoomScale){Bitmap btImage …...

猜猜 JavaScript 输出:(! + [] + [] + ![]).length
一起猜 最近看到一个很有意思的题,直接来看,下面这段代码的打印结果是什么? console.log((! [] [] ![]).length) 猜猜看,你的答案是什么,打在评论区。 我的答案是 undefined,正如我的英文名 为什么呢&a…...

MTK Android12静默安装接口
该文档就是在android12系统上提供一个广播接收器,app端发送一个广播,并且带入apk的地址就可以实现安装 1、广播注册 frameworks\base\services\core\java\com\android\server\policy\PhoneWindowManager.java 首先要导入的依赖 import android.app.P…...
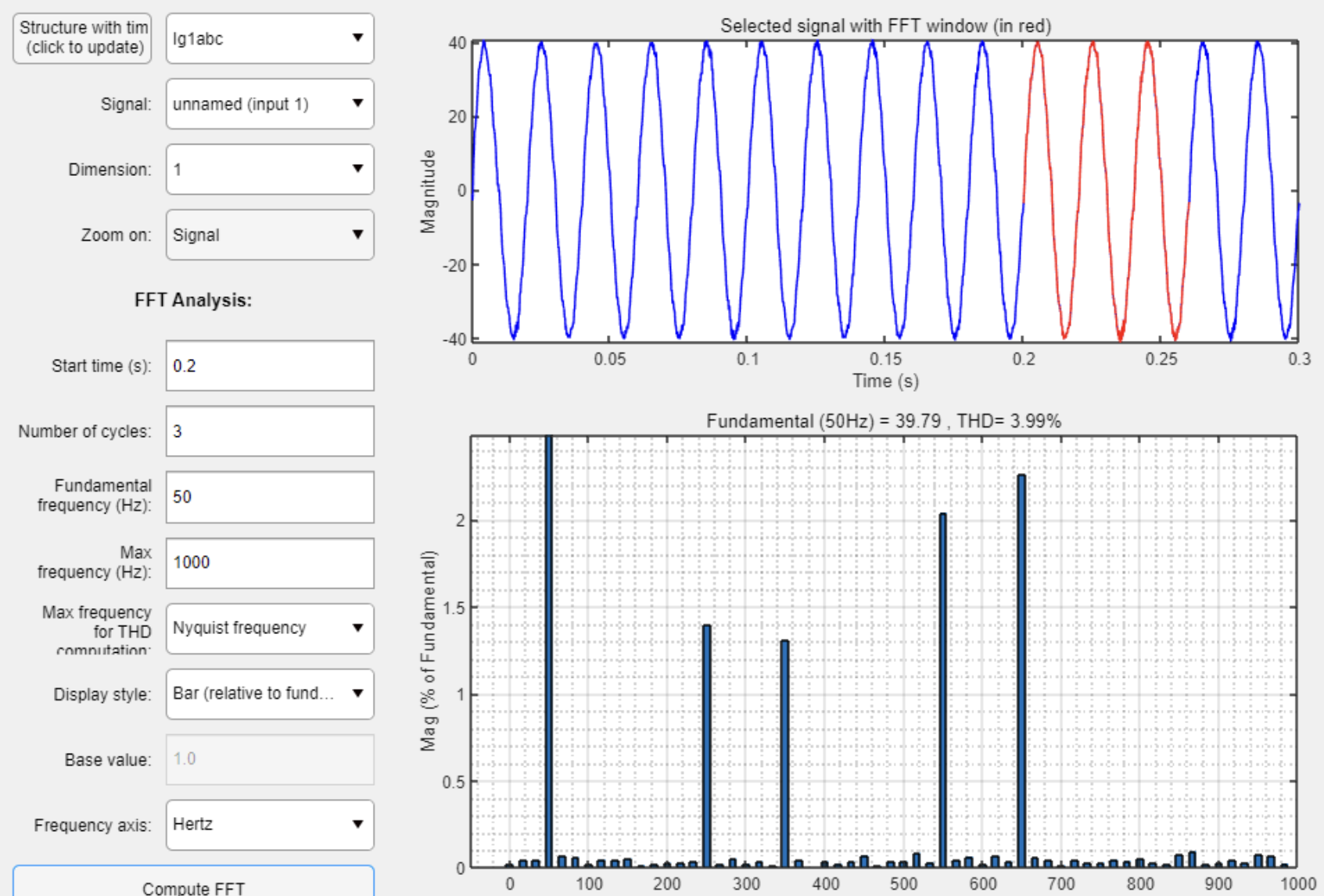
基于电容电流前馈与电网电压全前馈的三相LCL并网逆变器谐波抑制Simulink仿真
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Python数据攻略-Pandas与统计数据分析
统计学在数据分析中到底有多重要?在数据分析的世界里,统计学扮演着一角色。想象一下你是《三国志》游戏的数据分析师,任务是找出哪个武将最受玩家欢迎,哪些战役最具挑战性等。 你怎么做呢?这就需要统计学的力量了。 文章目录 基础统计方法描述性统计方差和标准差相关性和…...
【gcc】RtpTransportControllerSend学习笔记 1
本文是大神 https://www.cnblogs.com/ishen 的文章的学习笔记。主要是大神文章: webrtc源码分析(8)-拥塞控制(上)-码率预估 的学习笔记。大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。因为直接看大神的文章,自己啥也没记住,所以同时跟着看代码。跟…...

若依分离版-前端使用
1 执行 npm install --registryhttps://registry.npm.taobao.org,报错信息如下 npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: ktg-mes-ui3.8.2 npm ERR! Found: vue2.6.12 npm ERR! node_modu…...

微信小程序-2
微信开发文档 https://developers.weixin.qq.com/miniprogram/dev/framework/ 一、app.js中的生命周期函数与globalData(全局变量) 指南 - - - 小程序框架 - - - 注册小程序 删除app.js里的东西,输入App回车,调用生命周期 选项 - - - 重新打开此项目…...
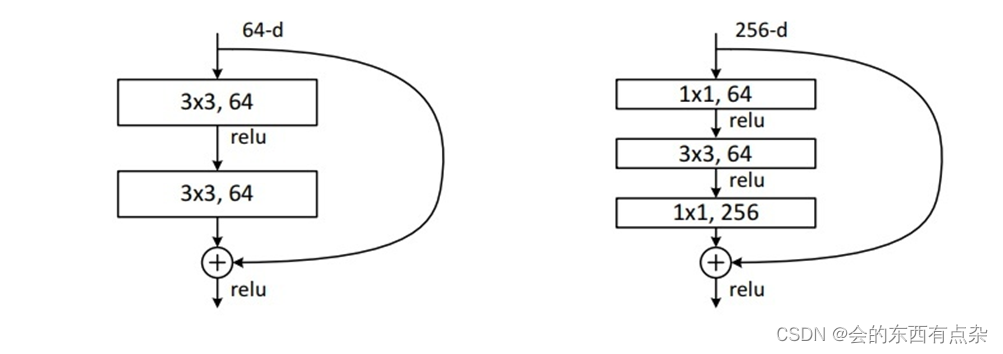
卷积神经网络的发展历史-ResNet
ResNet的产生 2015 年,Kaiming He 提出了ResNet(拿到了 2016 年 CVPR Best Paper Award),不仅解决了神经网络中的退化问题还在同年的ILSVRC和COCO 竞赛横扫竞争对手,分别拿下分类、定位、检测、分割任务的第一名。 R…...
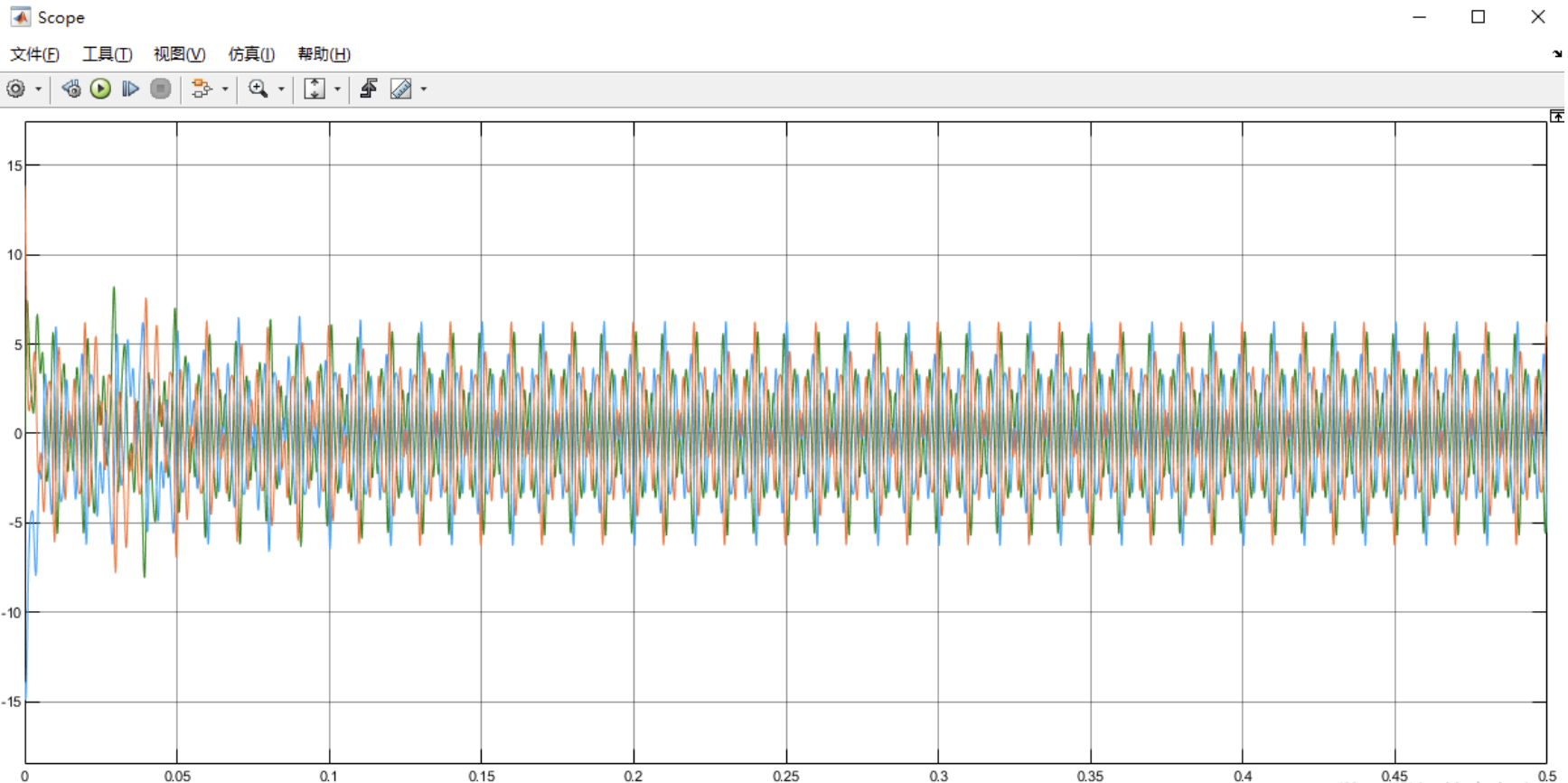
基于瞬时无功功率ip-iq的谐波信号检测Simulink仿真
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

node安装,nvm管理器
一、下载nvm,nvm-setup.exe https://github.com/coreybutler/nvm-windows/releases 二、配置NodeJS下载代理镜像(可选) 可以在NVM安装根目录下的setting.txt文件中,配置NodeJS下载代理镜像,解决在线安装NodeJS时速度…...
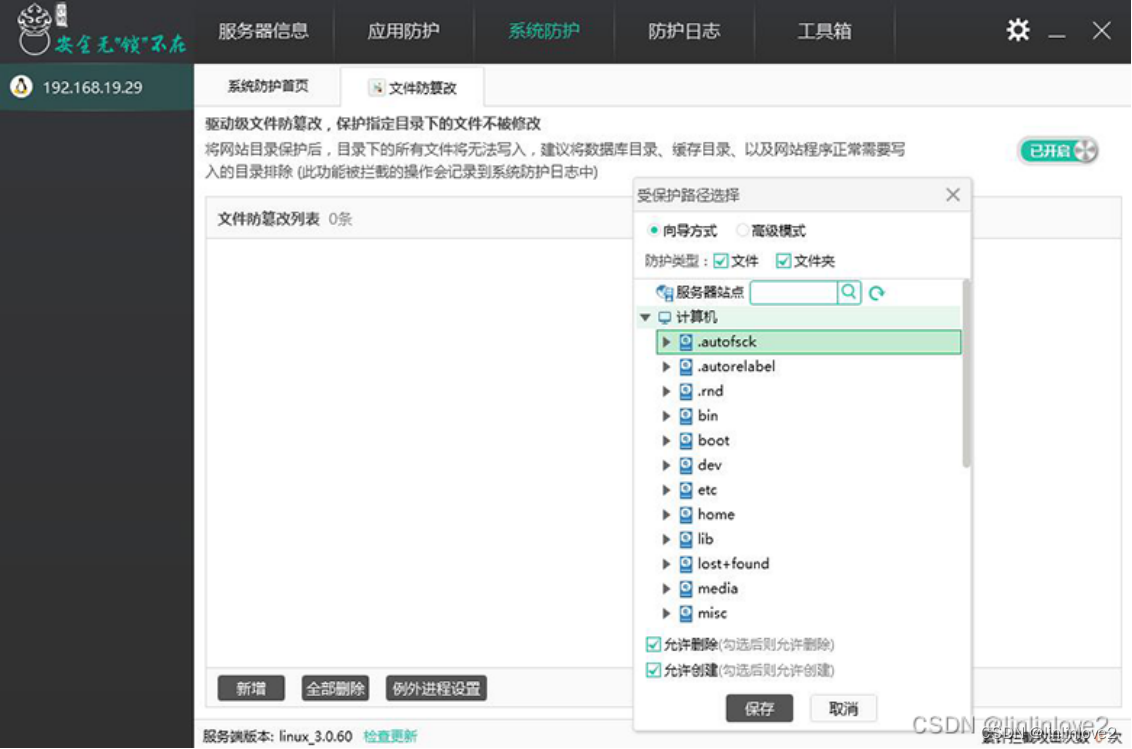
华为云云耀云服务器L实例评测|Ubuntu云锁防火墙安装搭建使用
华为云云耀云服务器L实例评测|Ubuntu安装云锁防火墙对抗服务器入侵和网络攻击 1.前言概述 华为云耀云服务器L实例是新一代开箱即用、面向中小企业和开发者打造的全新轻量应用云服务器。多种产品规格,满足您对成本、性能及技术创新的诉求。云耀云服务器L…...
C# OpenCvSharp 实现迷宫解密
效果 项目 代码 using OpenCvSharp; using System; using System.Drawing; using System.Windows.Forms;namespace OpenCvSharp_实现迷宫解密 {public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e…...
趣味工具箱小程序源码
趣味工具箱小程序源码,支持功能去水印,精选壁纸,图片压缩,文字生成二维码,图片加水印,模拟来电,手持弹幕,掷骰子…等 使用小工具,一个小程序有几十个功能。 源码下载&am…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
