代理IP与Socks5代理的技术奇妙之旅
随着数字化时代的崛起,网络工程师们日益承担着维护网络稳定性和保护数据安全的重任。在这个充满挑战的世界里,代理IP与Socks5代理技术成为了他们的秘密武器,本文将带您踏上一段技术奇妙之旅,深入了解这两项技术在不同领域中的应用。
1. 代理IP:穿越地域的魔法
跨界电商和出海业务需要企业在全球范围内扩展业务。而代理IP技术可以让网络工程师模拟不同地区的用户,突破地理限制,更好地了解市场需求,为企业拓展国际市场提供支持。这是一种技术上的魔法,让企业可以穿越地域,触及全球。
2. 爬虫:数据采集的魔杖
在信息时代,数据是黄金,而网络工程师是数据采集的魔法师。爬虫应用需要频繁访问网站,抓取宝贵的数据。代理IP技术的巧妙运用可以帮助网络工程师规避封禁,确保数据采集的连贯性。这是一种数据魔法,让企业能够汲取信息的力量,做出明智的决策。
3. 网络安全:数字世界的盾牌
网络工程师是数字世界的守护者,而代理IP与Socks5代理技术是他们的盾牌。代理IP可用于建立安全通道,保护数据传输的隐私。Socks5代理技术则能绕过网络审查和防火墙,提高网络的可访问性。这是一种安全魔法,保护着企业和用户的数字生活。
4. 游戏:优化娱乐的法宝
游戏领域对网络性能有极高要求,而Socks5代理技术可以帮助玩家降低游戏延迟,提高游戏体验。连接到最近的游戏服务器节点,玩家可以享受流畅的游戏乐趣。这是一种娱乐魔法,让游戏变得更加令人陶醉。
总结而言,代理IP与Socks5代理技术是网络工程师的秘密武器,用来应对跨界电商、爬虫、出海业务、网络安全和游戏等各种挑战。它们是技术世界的魔法,让网络工程师能够穿越地域、获取宝贵数据、保护网络安全和提高游戏体验。网络工程师不仅仅是技术的管理者,更是技术的魔法师,用技术的魔法为数字世界创造奇迹。
相关文章:

代理IP与Socks5代理的技术奇妙之旅
随着数字化时代的崛起,网络工程师们日益承担着维护网络稳定性和保护数据安全的重任。在这个充满挑战的世界里,代理IP与Socks5代理技术成为了他们的秘密武器,本文将带您踏上一段技术奇妙之旅,深入了解这两项技术在不同领域中的应用…...

自动化测试定位不到元素?可能是 frame 在搞鬼
很多人在用Splinter或Selenium定位页面元素的时候会遇到定位不到的问题,明明元素就在那儿,就是定位不到,这种情况很有可能是frame在搞鬼。 说白了就是网站上的网页A,又嵌入了其他网页B。你访问了网页A,在里面可以看到…...

uni-app 开发中,监听 input 键盘事件获取不到按下按键值怎么办?
uniapp 开发 H5 时,无法监听按钮键盘事件的原因以及解决方法。 问题描述: 不少 uni-app 开发者在使用 input 组件时,监听 keyup 事件时,获取不到键盘的 keyCode。编写的代码如下: <template><input keyup&…...
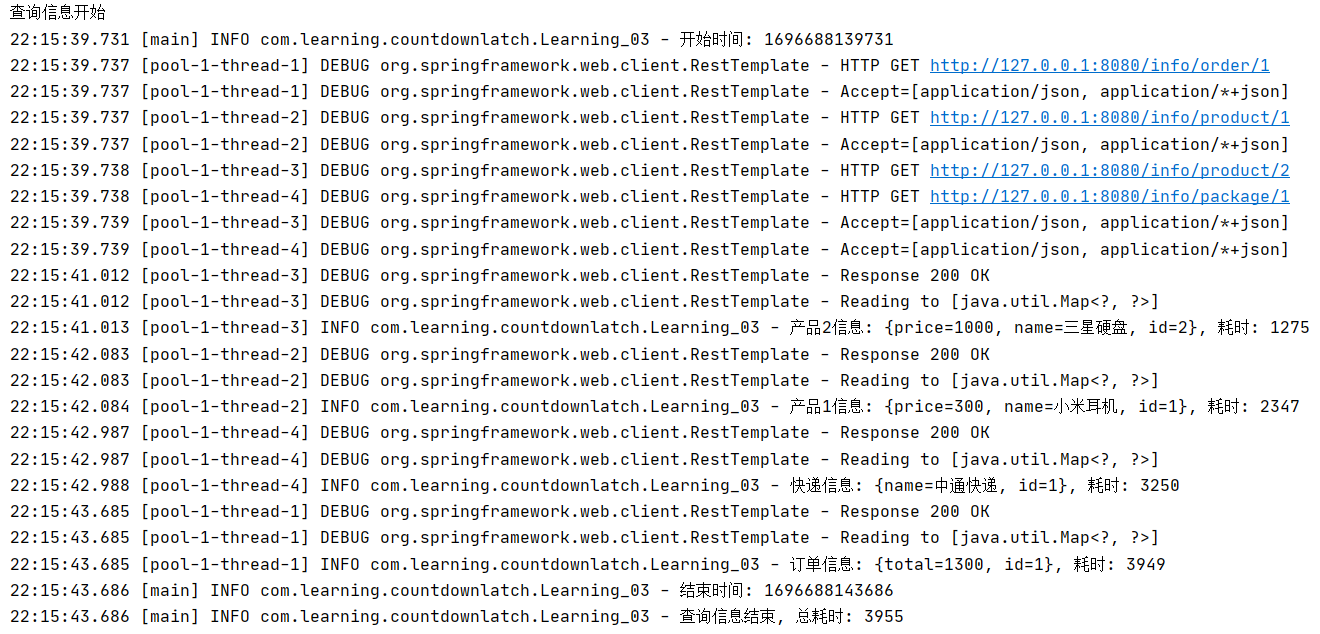
【juc】countdownlatch实现并发网络请求
目录 一、截图示例二、代码示例2.1 测试代码2.2 接口代码 一、截图示例 二、代码示例 2.1 测试代码 package com.learning.countdownlatch;import lombok.extern.slf4j.Slf4j; import org.springframework.web.client.RestTemplate;import java.util.Arrays; import java.uti…...
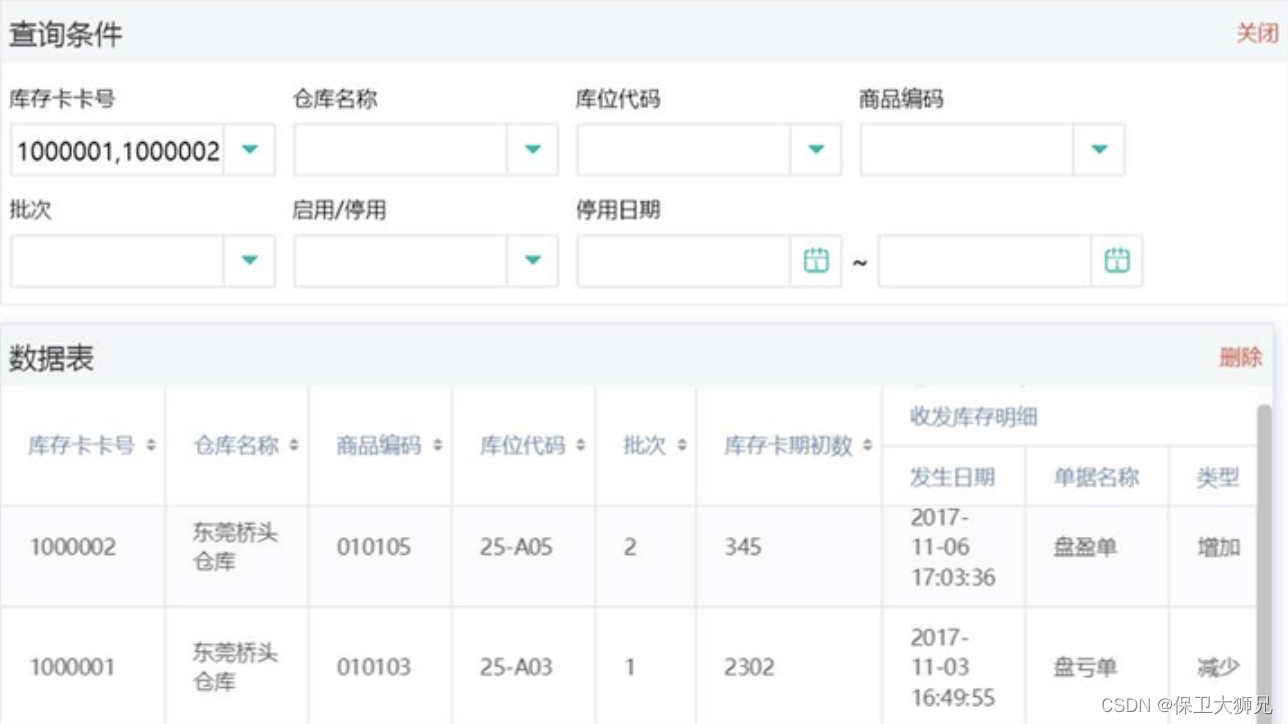
在供应链管理中,如何做好库存分析?库存分析有哪些监控指标?
在供应链管理中,库存分析是其重要的一环。库存分析的方法繁杂且广泛,选择正确的方法才能更好的进行库存分析,下面就为大家盘点一些常用的库存分析方法和监控指标,全程干货,建议收藏! 01 如何进行库存分析&…...

黑豹程序员-架构师学习路线图-百科:Database数据库
文章目录 1、什么是Database2、发展历史3、数据库排行网4、总结 1、什么是Database 当今世界是一个充满着数据的互联网世界,各处都充斥着大量的数据。即这个互联网世界就是数据世界。 支撑这个数据世界的基石就是数据库,数据库也可以称为数据的仓库。 …...

你相信光吗?黑灯工厂重新相信“光”
你知道“黑灯工厂”吗?望文生义,所谓黑灯工厂,就是可以不需要照明的工厂。全程流水线自动化生产,无人干预、无人值守,工厂变成黑匣子,原材料进去,成品出来,流水线上百分百自动化。 完…...

Ubuntu 20.04使用源码安装nginx 1.14.0
nginx安装及使用(详细版)是一篇参考博文。 http://nginx.org/download/可以选择下载源码的版本。 sudo wget http://nginx.org/download/nginx-1.14.0.tar.gz下载源代码。 sudo tar xzf nginx-1.14.0.tar.gz进行解压。 cd nginx-1.14.0进入到源代码…...

springboot框架拦截器中HttpServletRequest 请求如何区分是图片上传流还是普通的字符流?
在Spring Boot框架中的拦截器(Interceptor)中,可以通过检查Content-Type请求头来区分图片上传流和普通的字符流。 当客户端发送POST请求并携带文件时,Content-Type请求头通常会包含multipart/form-data或者类似的值。这表明该请求…...
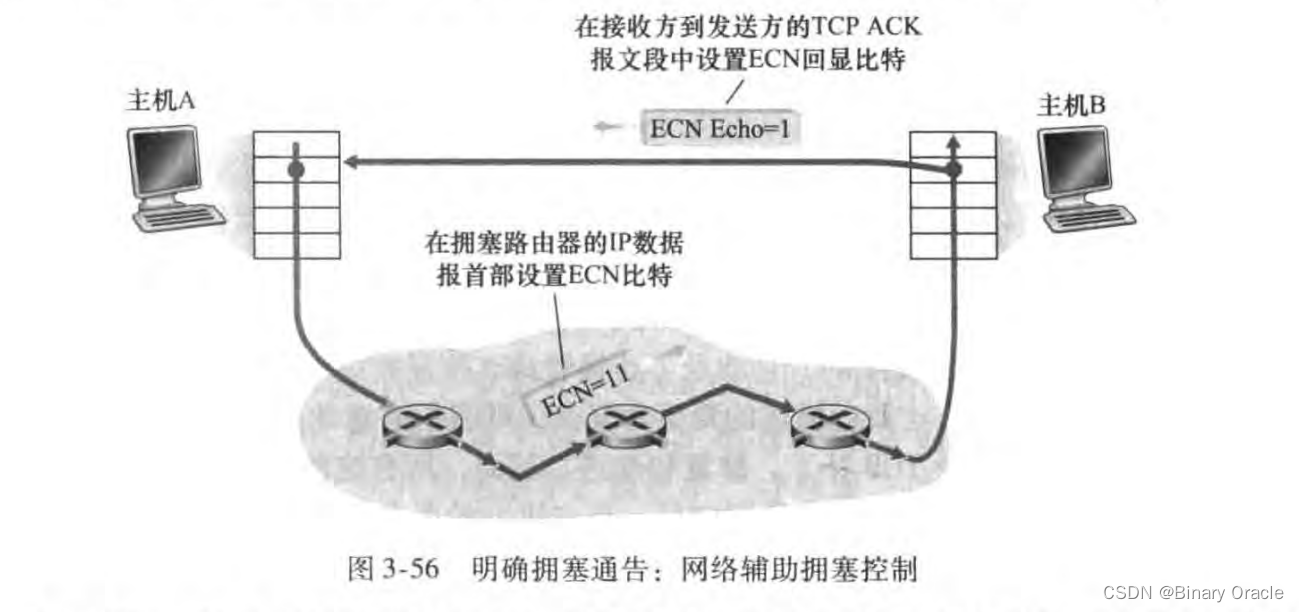
简单聊聊 TCP 协议
简单聊聊 TCP 协议 如何实现可靠传输 ?完全可靠存在比特差错存在丢包流水线可靠数据传输协议回退N步 (GBN)选择重传 (ARQ) 小结 TCPTCP 连接报文段结构序号和确认号 可靠数据传输避免重传超时时间加倍快速重传回退N步还是选择重传 流量控制连接管理拥塞控制拥塞原因拥塞控制方…...

钡铼BL124PN:简单快速转换Profinet到Ethernet/IP
钡铼技术BL124PN是一款高性能的Profinet转Ethernet/IP网关设备。该网关专为工业自动化领域设计,用于实现不同协议之间的互连和通信。BL124PN采用可靠稳定的硬件和先进的通信技术,具有以下主要特点: 协议转换能力:BL124PN能够将Pr…...

【golang】go 空结构体 详解 空结构体内容占用及大小
一、空结构体基础 空结构实例 和 空结构体变量 本质是一样的 1、所有空结构体地址都是一样的2、大小都为0(最独特的) package mainimport ("fmt""time""unsafe" )type EST struct { }func main() {// 一、基础// 空结构…...

身为产品经理该如何向客户推广API商品数据接口
在当今数字化的时代,API(Application Programming Interface,应用程序编程接口)已成为各种软件应用程序之间交互数据的主要方式。API商品数据接口作为一种特殊类型的API,能够让不同的系统之间共享商品数据,…...

【数据结构】460. LFU 缓存
460. LFU 缓存 解题思路 get操作 返回key对应的val 然后增加对应的freq插入操作 如果key已经存在 直接进行更新 如果不存在 但是容器已经满了 直接进行删除freq最小的Key 之后进行插入 class LFUCache {// key到 val的映射 KVHashMap<Integer,Integer> keyToVal;// …...
:阿里云nls服务使用示例)
文字转语音播报模块(一):阿里云nls服务使用示例
一、业务场景 最近笔者在业务中涉及到语音告警的模块,需要讲告警内容以文件或流形式返回给前端进行语音播报,具体的分析与处理如下 二、业务分析 首先告警内容提示信息这里做的处理是通过专门字段去存储、编辑,根据拟定好的代码逻辑判断是…...
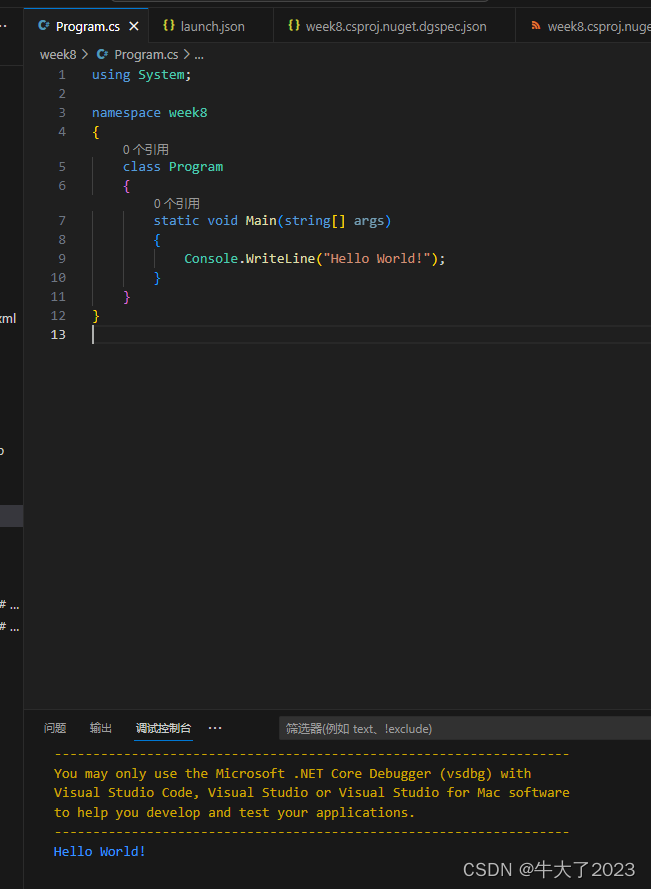
Vscode配置C#编程环境(win10)
目录 1、安装好Vscode 2、下载安装.NetCore SDK 3、配置C#环境 3.1 打开Vscode并下载扩展 3.2 Vscode中打开文件夹并配置环境 3.3 调试运行 1、安装好Vscode 2、下载安装.NetCore SDK 官网如下,下载完成后双击打开一路走到底就行.NetCore SDK官网 软件显示安…...

python:xlrd 读取 Excel文件,显示在 tkinterTable 表格中
pip install xlrd xlrd-1.2.0-py2.py3-none-any.whl (103 kB) 摘要: Library for developers to extract data from Microsoft Excel (tm) spreadsheet files pip install tkinterTable tkintertable-1.3.3.tar.gz (58 kB) 摘要: Extendable table class for Tkinter 源代…...
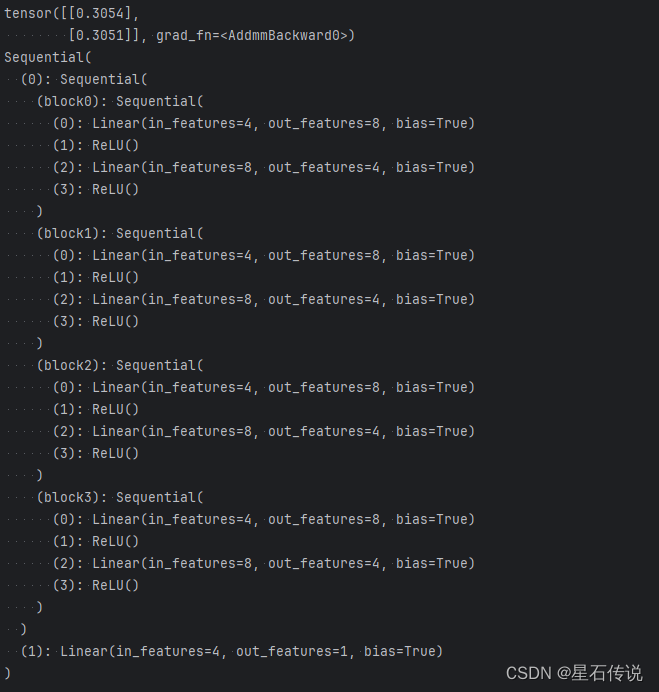
深度学习——深度学习计算一
深度学习——深度学习计算一 文章目录 前言一、层和块1.1. 自定义块1.2. 顺序块1.3. 在前向传播函数中执行代码1.4. 小结 二、参数管理2.1. 参数访问2.1.1. 目标参数2.1.2. 一次性访问所有参数2.1.3. 从嵌套块收集参数 2.2. 参数初始化2.2.1. 内置初始化2.2.2. 自定义初始化 2.…...

yolov5及yolov7实战之剪枝
之前有讲过一次yolov5的剪枝:yolov5实战之模型剪枝_yolov5模型剪枝-CSDN博客 当时基于的是比较老的yolov5版本,剪枝对整个训练代码的改动也比较多。最近发现一个比较好用的剪枝库,可以在不怎么改动原有训练代码的情况下,实现剪枝的…...
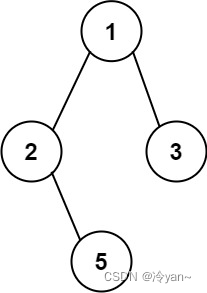
力扣第257题 二叉树的所有路径 c++ 树 深度优先搜索 字符串 回溯 二叉树
题目 257. 二叉树的所有路径 简单 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [1,2,3,null,5] 输出:["1->2-&g…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
