金融数学方法:牛顿法
目录
- 1.牛顿法
- 1.1 牛顿法介绍
- 1.2 算法步骤
- 2. 具体算例
- 3.总结
1.牛顿法
1.1 牛顿法介绍
牛顿法(Newton’s method),也被称为牛顿-拉夫森方法(Newton-Raphson method),是一种用于数值逼近根的迭代方法。它是由英国科学家艾萨克·牛顿在17世纪提出的。
牛顿法的基本思想是通过不断迭代来逼近一个函数的根。它利用函数的局部线性逼近,通过找到切线与x轴的交点来逼近函数的根。具体而言,牛顿法使用一个初始猜测值作为起点,然后根据函数和它的导数在该点的值,计算出切线与x轴的交点作为下一个猜测值。通过不断重复这个过程,可以更接近函数的根。
1.2 算法步骤
Step1: 选择一个初始猜测值:选择一个接近函数 f ( x ) f(x) f(x)零点的 x 0 x_0 x0。
Step2: 计算在点 x 0 x_0 x0处的函数值 f ( x 0 ) f(x_0) f(x0)和导数 f ′ ( x 0 ) f\prime\left( x_0 \right) f′(x0)。
Step3: 计算穿过点 ( x 0 , f ( x 0 ) (x_0,f(x_0) (x0,f(x0)且斜率为 f ′ ( x 0 ) f\prime\left( x_0 \right) f′(x0)的直线与 x x x轴的交点 x 1 x_1 x1,也就是方程 f ′ ( x 0 ) ( x − x 0 ) + f ( x 0 ) = 0 f \prime(x_0)(x-x_0)+f(x_0)=0 f′(x0)(x−x0)+f(x0)=0的解,即 x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) x_1=x_0-\frac{f\left( x_0 \right)}{f\prime\left( x_0 \right)} x1=x0−f′(x0)f(x0)。
Step4: 使用牛顿法的迭代公式 x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f\left( x_n \right)}{f\prime\left( x_n \right)} xn+1=xn−f′(xn)f(xn)进行迭代,等到 f ( x n ) f(x_n) f(xn)足够小时(可以设置一个终止条件),就认为数值解足够接近真实解,然后停止迭代。
2. 具体算例
利用牛顿法求 e x = 2 e^x=2 ex=2的解,选取初始点 x 0 = 1 x_0=1 x0=1,然后利用牛顿法迭代公式进行求解。
具体的python程序如下:
import numpy as np
def hanshu(x):return np.exp(x)-2
def daoshu(x):return np.exp(x)
def newtown(x0):d=hanshu(x0)count=0while d>0.000001 and count<100:x1=x0-d/daoshu(x0)x0=x1d=hanshu(x0)count+=1return x0,count
print(newtown(1))
求解结果:(0.6931475810597714, 3)
方程 e x = 2 e^x=2 ex=2的实际解为0.6931471805599453,可见利用牛顿法迭代了3次就得到了一个精度很高的结果,收敛速度比较快。
3.总结
牛顿法在数学和科学工程领域广泛应用,特别是在求解非线性方程、最优化问题和曲线拟合等任务中。牛顿法具有快速收敛的特点,但它对初始值的选择比较敏感,可能会陷入局部最优解。因此,在使用牛顿法时需要考虑初始值的选择和算法的收敛性分析。
相关文章:

金融数学方法:牛顿法
目录 1.牛顿法1.1 牛顿法介绍1.2 算法步骤 2. 具体算例3.总结 1.牛顿法 1.1 牛顿法介绍 牛顿法(Newton’s method),也被称为牛顿-拉夫森方法(Newton-Raphson method),是一种用于数值逼近根的迭代方法。它是…...

MongoTemplate | 多条件查询
MongoTemplate查询 Resource private MongoTemplate mongoTemplate;public <T> List<T> getDataList(String param1, Long param2, Class<T> clazz) {// 构建queryQuery query constructQuery(param1, param2);// 查询return mongoTemplate.find(query, cl…...

优秀程序员是怎么思考的?
首发日更公 Z 号:十二又十三 作为一名优秀的程序员,思考是我们工作中最重要的一部分。它不仅能够帮助我们解决问题,还能够提升我们的技术水平和职业发展。那么,优秀程序员是如何思考的呢?本文将为您介绍一个思考框架和…...

【juc】countdownlatch实现游戏进度
目录 一、截图示例二、代码示例 一、截图示例 二、代码示例 package com.learning.countdownlatch;import java.util.Arrays; import java.util.Random; import java.util.concurrent.CountDownLatch; import java.util.concurrent.ExecutorService; import java.util.concurr…...

Spring Webflux HttpHandler源码整理
HttpHandler的构造 自动启动配置类:HttpHandlerAutoConfigurationBean public HttpHandler httpHandler(ObjectProvider<WebFluxProperties> propsProvider) {HttpHandler httpHandler WebHttpHandlerBuilder.applicationContext(this.applicationContext).…...
Qt扩展-Advanced-Docking 简介及配置
Advanced-Docking 简介及配置 一、概述二、项目结构三、安装配置四、代码测试 一、概述 Advanced-Docking 是类似QDockWidget 功能的多窗口停靠功能的库。很像visual stdio 的 停靠功能,这个库对于停靠使用的比较完善。很多的软件都使用了这个框架。 项目源地址&a…...

Decorator
Decorator 动机 在某些情况下我们可能会“过度地使用继承来扩展对象的功能”, 由于继承为类型引入的静态特质,使得这种扩展方式缺乏灵活性; 并且随着子类的增多(扩展功能的增多),各种子类的组合ÿ…...
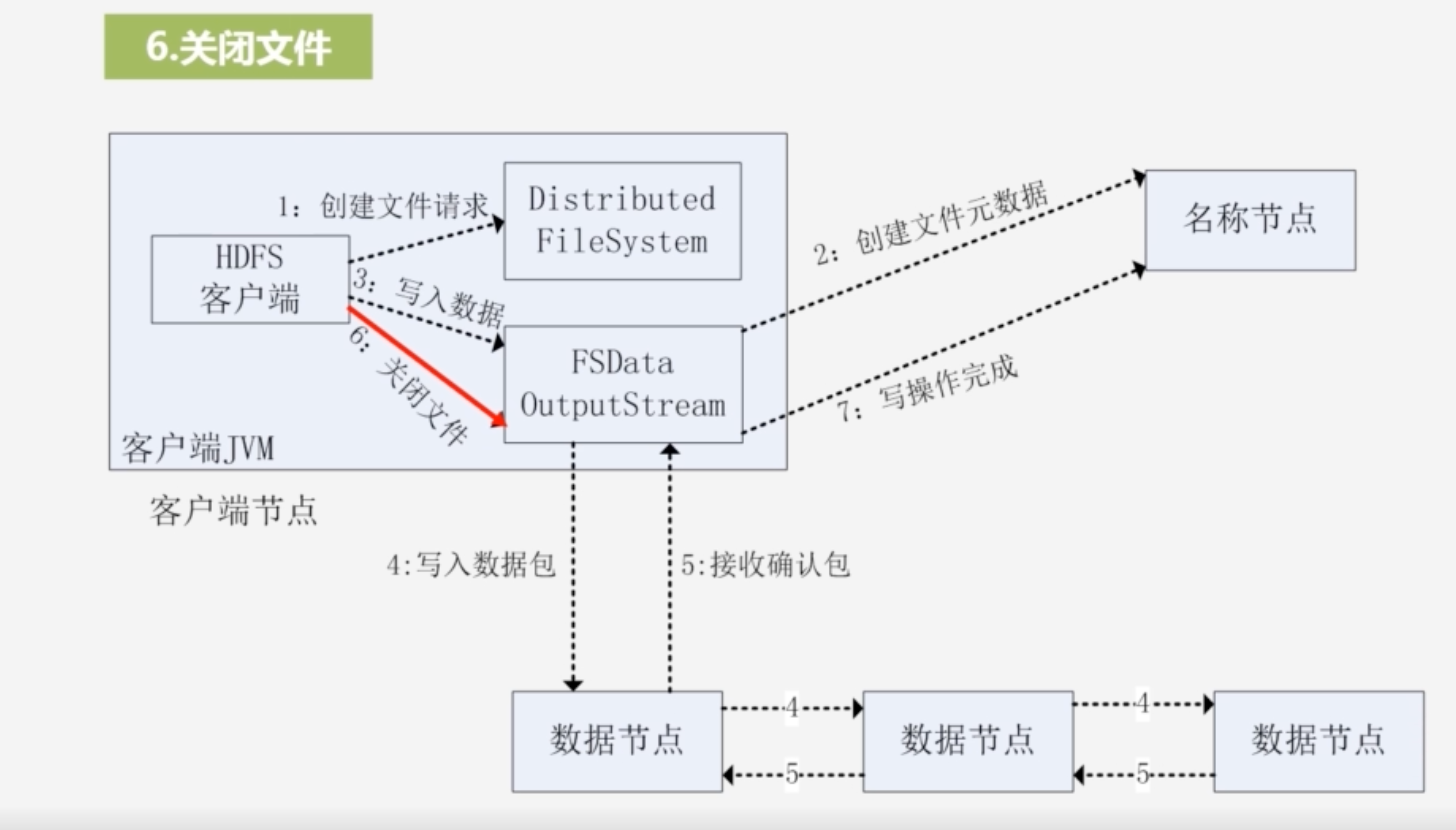
分布式文件系统HDFS(林子雨慕课课程)
文章目录 3. 分布式文件系统HDFS3.1 分布式文件系统HDFS简介3.2 HDFS相关概念3.3 HDFS的体系结构3.4 HDFS的存储原理3.5 HDFS数据读写3.5.1 HDFS的读数据过程3.5.2 HDFS的写数据过程 3.6 HDFS编程实战 3. 分布式文件系统HDFS 3.1 分布式文件系统HDFS简介 HDFS就是解决海量数据…...

CSS中:root伪类的使用
在CSS中,:root是一个伪类选择器,它选择的是文档树的根元素。在HTML文档中,这个根元素通常是<html>。:root伪类选择器常常被用于定义全局的CSS变量或者设置全局的CSS样式。 例如,你可以使用:root来定义一个全局的字体大小&a…...
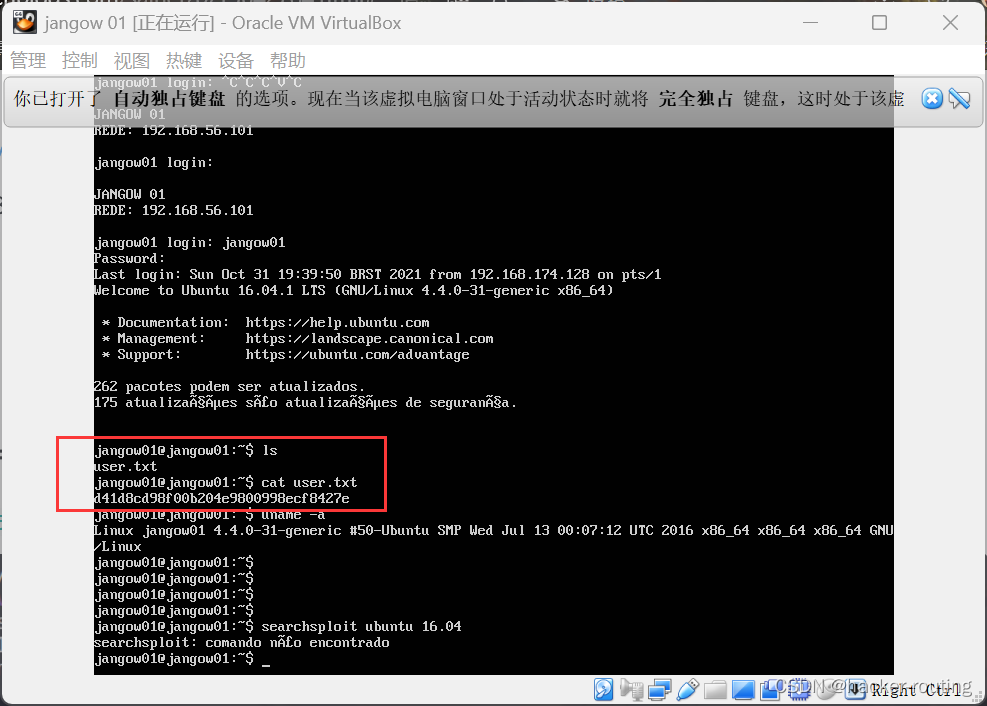
VulnHub JANGOW
提示(主机ip分配问题) 因为直接在VulnHub上下载的盒子,在VMware上打开,默认是不分配主机的 所以我们可以在VirtualBox上打开 一、信息收集 发现开放了21和80端口,查看一下80端口 80端口: 检查页面后发现…...

OpenMesh 获取网格面片各个顶点
文章目录 一、简介二、实现代码三、实现效果一、简介 OpenMesh中有很多循环器,这里便是其中一种面顶点循环器,以此来获得面片的各个顶点。 二、实现代码 #define _USE_MATH_DEFINES #include <iostream> #include <unordered_map>...

【前端设计模式】之原型模式
原型模式特性 原型模式(Prototype Pattern)是一种创建型设计模式,它通过克隆现有对象来创建新对象,而不是通过实例化类。原型模式的主要特性包括: 原型对象:原型对象是一个已经存在的对象,它作…...

软件设计原则
设计原则 一、单一原则 1. 如何理解单一职责原则 单一职责原则(Single Responsibility Principle,简称SRP),它要求一个类或模块应该只负责一个特定的功能。实现代码的高内聚和低耦合,提高代码的可读性和可维护性。 …...
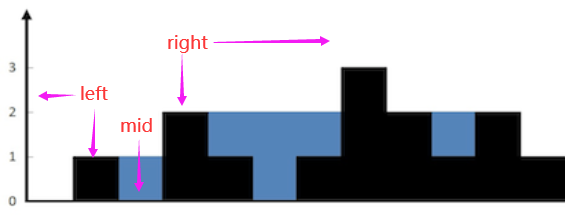
【面试HOT100】哈希双指针滑动窗口
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于LeetCodeHot100进行的,每个知识点的修正和深入主要参考…...
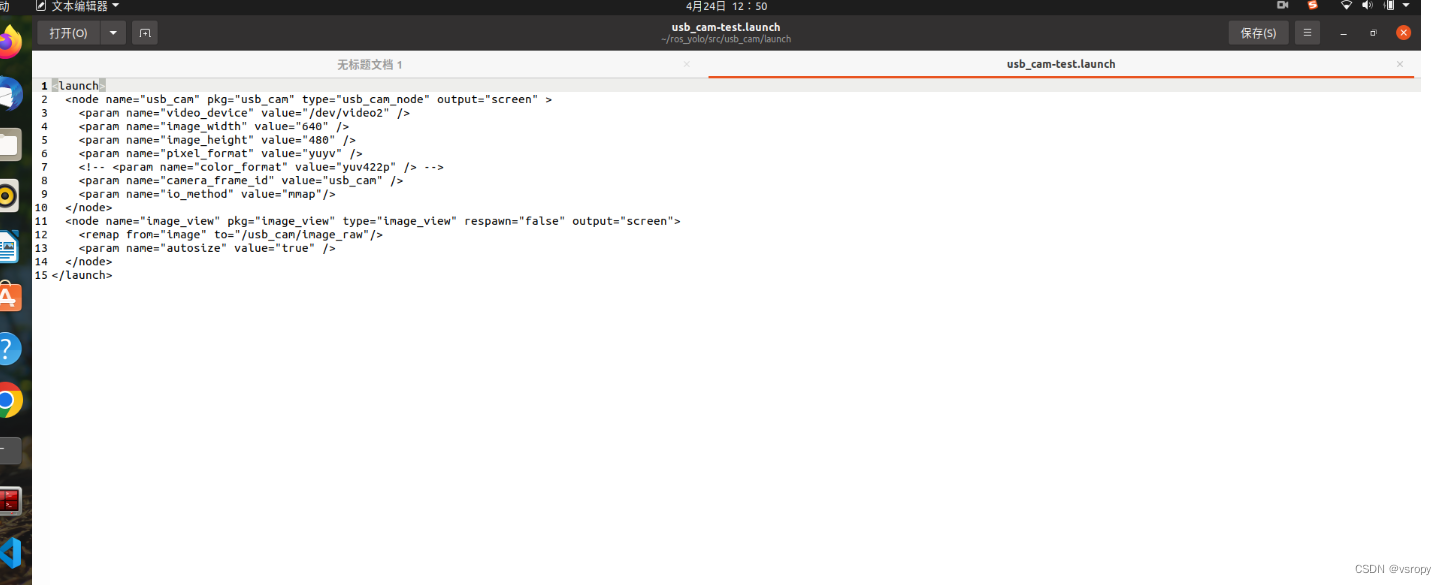
Ubuntu20.04 配置 yolov5_ros 功能包记录
文章目录 本文参考自博主源801,结合自己踩坑后修改 项目地址:https://github.com/mats-robotics/yolov5_ros 1.新建工作空间 新建一个工作空间 yolo_ros(名字可自定义),在 yolo_ros 下新建文件夹 src 并catkin_make进行编译 2. 安装相机驱动,可以选用较为主流的 usb_cam 或…...
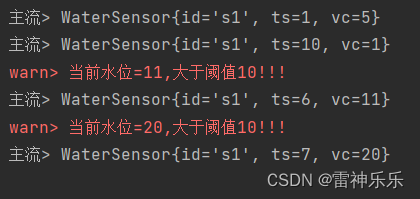
Flink的处理函数——processFunction
目录 一、处理函数概述 二、Process函数分类——8个 (1)ProcessFunction (2)KeyedProcessFunction (3)ProcessWindowFunction (4)ProcessAllWindowFunction ÿ…...

Linux系统中的ps命令详解及用法介绍
文章目录 一、介绍ps命令A. ps命令的作用B. ps命令的参数 二、常见的ps命令用法A. 显示所有进程信息B. 显示指定进程信息C. 显示指定用户的进程信息D. 按CPU使用率排序显示进程信息E. 按内存使用率排序显示进程信息 三、进一步了解ps命令A. 显示进程树信息B. 显示线程和进程关系…...

机器学习笔记 - 基于pytorch、grad-cam的计算机视觉的高级可解释人工智能
一、pytorch-gradcam简介 Grad-CAM是常见的神经网络可视化的工具,用于探索模型的可解释性,广泛出现在各大顶会论文中,以详细具体地描述模型的效果。Grad-CAM的好处是,可以在不额外训练的情况下,只使用训练好的权重即可获得热力图。 1、CAM是什么? CAM全称Class Activa…...

Python 编程基础 | 第五章-类与对象 | 5.1、定义类
一、类 1、定义类 Python中使用class关键字定义类,class之后为类的名称并以:结尾,类的结构如下: class 类名:多个(≥0)类属性...多个(≥0)类方法...下面定义一个Dog类,如…...
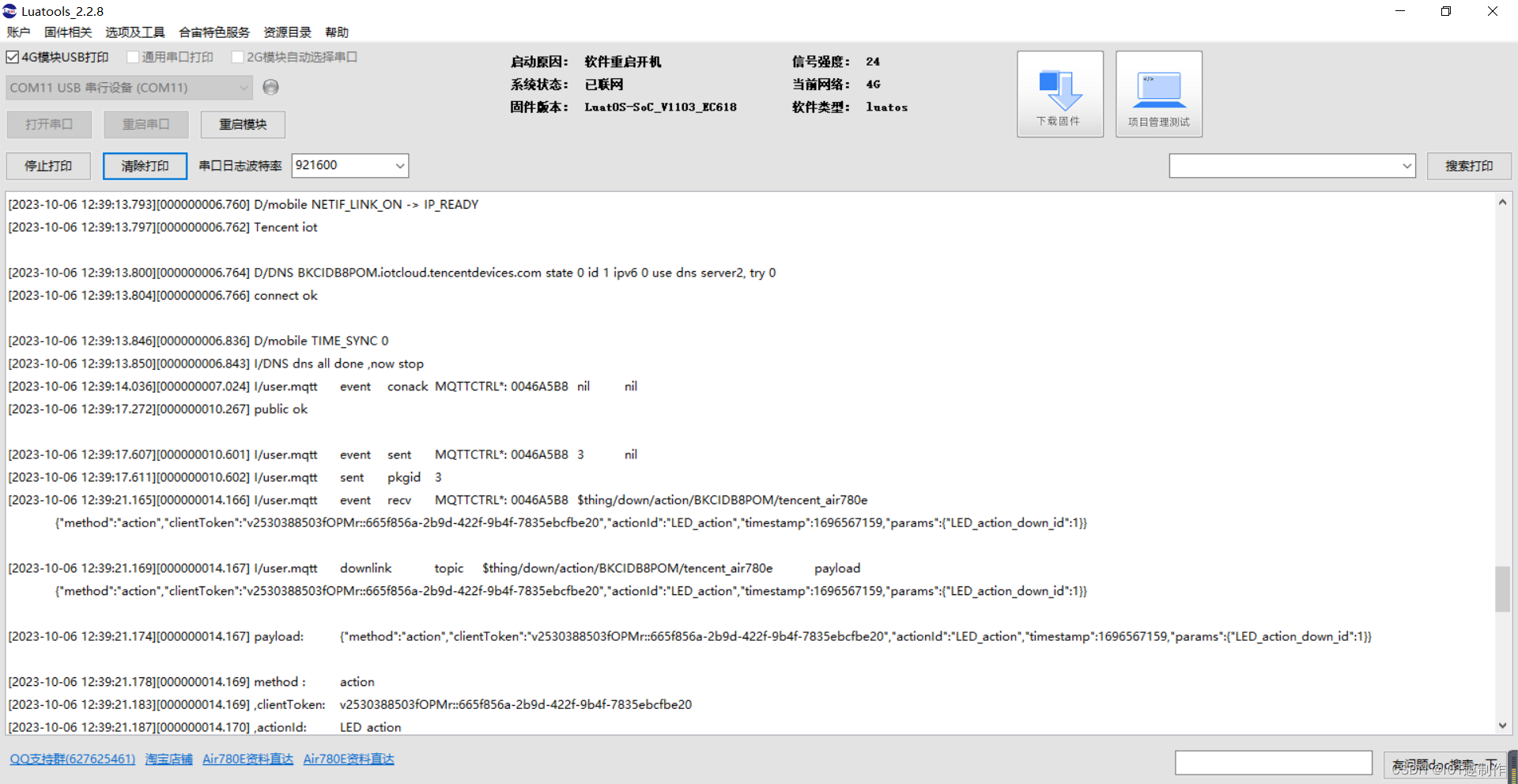
合宙Air780e+luatos+腾讯云物联网平台完成设备通信与控制(属性上报+4G远程点灯)
1.腾讯云物联网平台 首先需要在腾讯云物联网平台创建产品、创建设备、定义设备属性和行为,例如: (1)创建产品 (2)定义设备属性和行为 (3)创建设备 (4)准备参…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
