ACM 记忆化搜索
一.记忆化搜索概述
1.概念
搜索是一种简单有效但是效率又很低下的算法结构,其低效的原因主要在于存在很多重叠子问题。而记忆化搜索则是在搜索的基础上,利用数组来记录已经计算出来的重叠子问题状态,进行合理化的剪枝,从而降低时间复杂度。这个记录状态的过程就是记忆化的过程,我们需要找到不同搜索层次之间的子问题、状态转移关系,这与动态规划的思想又不谋而合。
简单来说,记忆化搜索是一种典型的空间换时间的思想,记忆化搜索 = 深度优先搜索实现 + 动态规划思想(记录状态、剪枝)。
2.图示
此处以某个记忆化搜索题目的结构树为例。在搜索过程中,我们将问题的搜索树画出来如下所示。左侧为暴力搜索的搜索树,而右侧为记忆化搜索剪枝的搜索树。
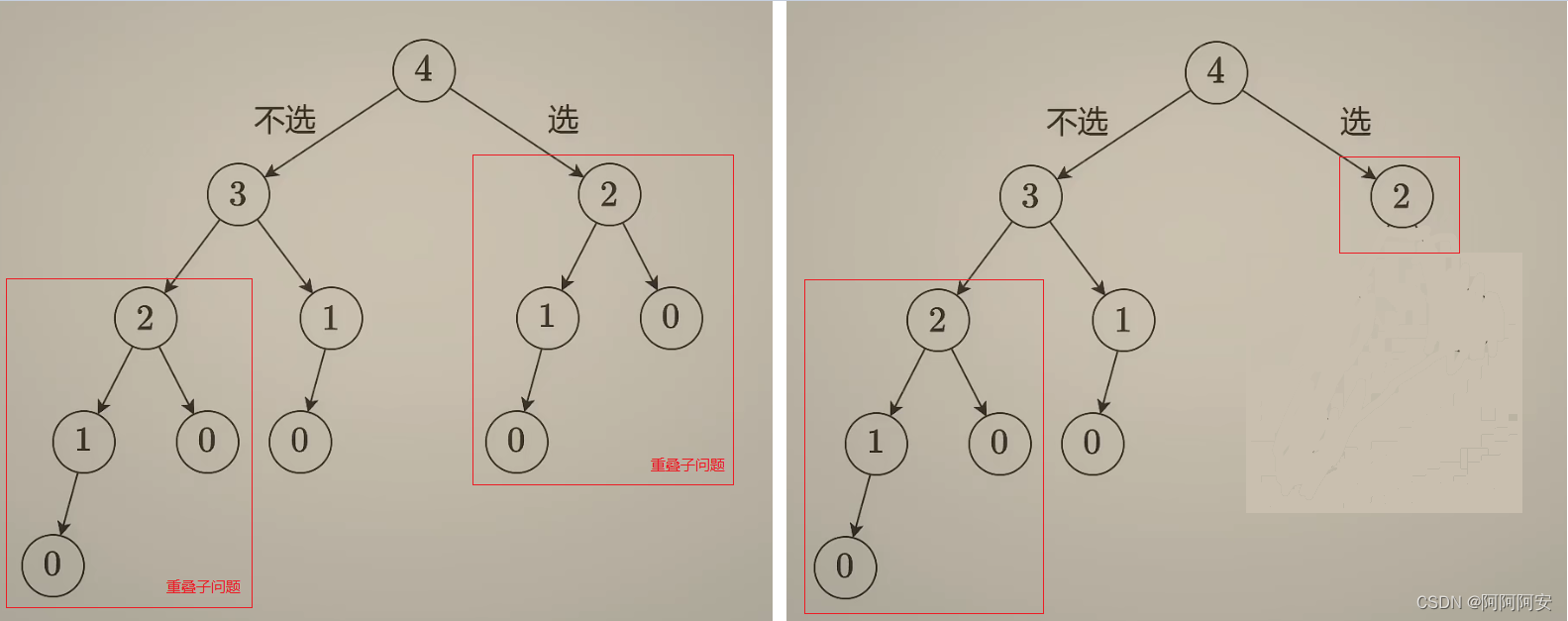
记忆化搜索可以看作是动态规划的前置过程,或者说记忆化搜索一般是自顶向下的,而动态规划一般是自底向上的。
二.例题
1.LeetCode 45. 跳跃游戏改
给定一个长度为 n 的整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处(0 <= j <= nums[i])
返回到达
nums[n - 1]的最小跳跃次数。已知跳跃次数有上限K,若无法在K次内到达则返回 -1
(1)记忆化搜索
对于该题,我们可以先求出到达终点的最小跳跃次数 t,然后比较 t 与上限 K 的大小,若t > K则返回 -1 。
按照搜索的思想来说,我们在到达某个索引 i 时,该位置到达终点的最小跳跃次数取决于 min(dfs(i) , dfs(i+j) + 1),0 <= j <= nums[i] ;按照记忆化的思想,像最短路一样,某个位置 i 到达终点的最小跳跃次数应该是确定的,属于重叠子问题,不应该重复搜索,因此可以使用数组记录每个位置的最小次数。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10000 + 7;
int n,k,nums[maxn],mem[maxn];int dfs(int index){if(index >= n-1)return 0;if(mem[index]!=-1)return mem[index];//记忆化int ans = -1;for(int i = 1;i<=nums[index];i++){int res = dfs(index+i)+1;if(res != 0){ans = ans==-1?res:min(ans,res);}}return mem[index] = ans;
}int main()
{memset(mem,-1,sizeof(mem));scanf("%d%d",&n,&k);for(int i = 0;i<n;i++){scanf("%d",&nums[i]);}dfs(0);if(mem[0] == -1 || mem[0] > k)printf("-1\n");else printf("%d\n",mem[0]);
}
(2)贪心
记忆化搜索的方式可行,但是复杂度还是有点高会超时。我们重新来审视这个题,每个位置处的跳跃距离是固定的、相互独立的,与之前的子节点和之后的子节点都是没关系的,也就是说该题其实与动态规划思想无关。
考虑现在跳到了位置 i ,那么接下来应该选择跳到 i+1 ~ i+nums[i] 的哪个位置呢?答案是「贪心」地选择能跳跃到距离最后一个位置最远的那个位置(即使得“探索序列”能够拓宽最远的那个位置),原因是以该位置为下一次起跳点所能到达的地方,由于其是最远的,所以能够覆盖其他所有的起跳点位置范围,这肯定是最优的。
当一次 跳跃 结束时,从下一个格子开始,到现在 能跳到最远的距离,都 是下一次 跳跃 的 起跳点。所以跳完一次之后,不断更新维护下一次 起跳点的范围。在新的范围内跳,更新 能跳到最远的距离。
int jump(int len){int ans = 0;int start = 0,last = 0; //初始起跳范围 [0,0] 闭区间while(last < len - 1){int maxpos = 0;//选择下一次跳哪个for(int i = start;i<=last;i++){maxpos = max(maxpos,i+nums[i]);}start = last+1; // 下一次起跳点范围开始的格子last = maxpos; // 下一次起跳点范围结束的格子ans++; // 跳跃次数}return ans;
}
2. 青蛙过河
一只青蛙想要过河。 假定河流被等分为若干个单元格,并且在每一个单元格内都有可能放有一块石子(也有可能没有)。 青蛙可以跳上石子,但是不可以跳入水中。
假设河流中一共有 n 个石子,给你每个石子的河流单元格位置的列表 stones(用单元格序号升序表示), 请判定青蛙能否成功过河(即能否在最后一步跳至最后一块石子上)。
开始时, 青蛙默认已站在第一块石子上,并可以假定它第一步只能跳跃一个单位(即只能从单元格1 跳至单元格 2 )。如果青蛙上一步跳跃了 k 个单位,那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意,青蛙只能向前方(终点的方向)跳跃。
输入:stones = [0,1,3,5,6,8,12,17] 输出:true 解释:青蛙可以成功过河,按照如下方案跳跃:跳 1 个单位到第 2 块石子, 然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子, 然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后,跳 5 个单位到第 8 个石子(即最后一块石子)。
该题题意与上一题的跳跃游戏类似,但是二者很大的一个不同就是每个位置的跳跃范围:跳跃游戏中每个位置的跳跃范围是固定的、相互独立的,而该题中每个位置的跳跃范围受到上一次跳跃的影响,具有子结构,因此该题优先考虑动态规划或记忆化搜索。
对于记忆化搜索来说,我们可以仍然去搜索所有可能的路径。但是对于每个节点来说,他的状态主要受到两个因素的影响:当前所在 stone 下标位置、上一次跳的步长,这两个因素决定了该位置后续的最优解。因此我们可以使用一个二维数组 dp[i][j] 保留位置 i 时,上个步长为 j 时的能否到达状态,以此进行记忆化搜索。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10000 + 7;
int n,stones[maxn];
vector<unordered_map<int, bool>> dp;bool dfs(int index,int preSteps){if(index == n-1)return true;if(index >= n)return false;if(dp[index].count(preSteps))return dp[index][preSteps];bool res = false;for(int i = preSteps-1;i<=preSteps+1;i++){if(i<=0)continue;int nextpos = lower_bound(stones+index, stones+n, stones[index]+i) - stones;if(nextpos < n && stones[nextpos] == stones[index]+i){res = dfs(nextpos,i);if(res)break;}}return dp[index][preSteps] = res;
}int main()
{scanf("%d",&n);dp.resize(n); // 初始化 vector 空间长度,int默认填充0,此处默认填充 空mapfor(int i = 0;i<n;i++){scanf("%d",&stones[i]);}bool ans = dfs(0,0);if(ans)printf("true\n");else printf("false\n");return 0;
}相关文章:

ACM 记忆化搜索
一.记忆化搜索概述 1.概念 搜索是一种简单有效但是效率又很低下的算法结构,其低效的原因主要在于存在很多重叠子问题。而记忆化搜索则是在搜索的基础上,利用数组来记录已经计算出来的重叠子问题状态,进行合理化的剪枝,从而降低时…...

spring框架常用注解简单说明
1、Configuration:标注在类上,相当于把当前类作为spring的xml配置文件中的; 2、Bean:标注在方法上,相当于spring配置文件中的; 3、Service:标注在类上,表明当前类是一个服务层的Be…...

2023-02-24 mysql/innodb-聚合-临时表避免OOM-使用磁盘文件-分析
摘要: mysql/innodb在执行聚合时, 当聚合的数据量太大时, 也就是临时表的大小超过tmp_table_size 限制时, 将进行写磁盘操作, 以避免OOM。 本文记录聚合数据写磁盘的操作。 参考: https://dev.mysql.com/doc/refman/5.7/en/server-system-variables.html#sysvar_tmp_table_…...
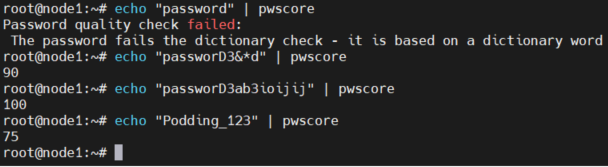
cracklib与libpwquality 评估密码的安全性
一、cracklib 检测密码强弱linux中采用pam pam_cracklib module来实现对密码强度的检测,可以通过配置让linux系统自动检测用户的密码是否为弱密码。yuminstall cracklib # centos apt-get install libcrack2 # ubuntu # 如果需要依赖此库做开发的话需要安装这个 y…...

【Java】保证并发安全的三大特性
一、并发编程三大特性的定义和由来 并发编程这三大特性就是为了在多个线程交替执行任务的过程中保证线程安全性。 二、为什么会出现线程不安全的现象呢? 接下来我们从这三个特性切入来介绍线程不安全的原因。 1.原子性: 一组操作要么全部执行&#…...
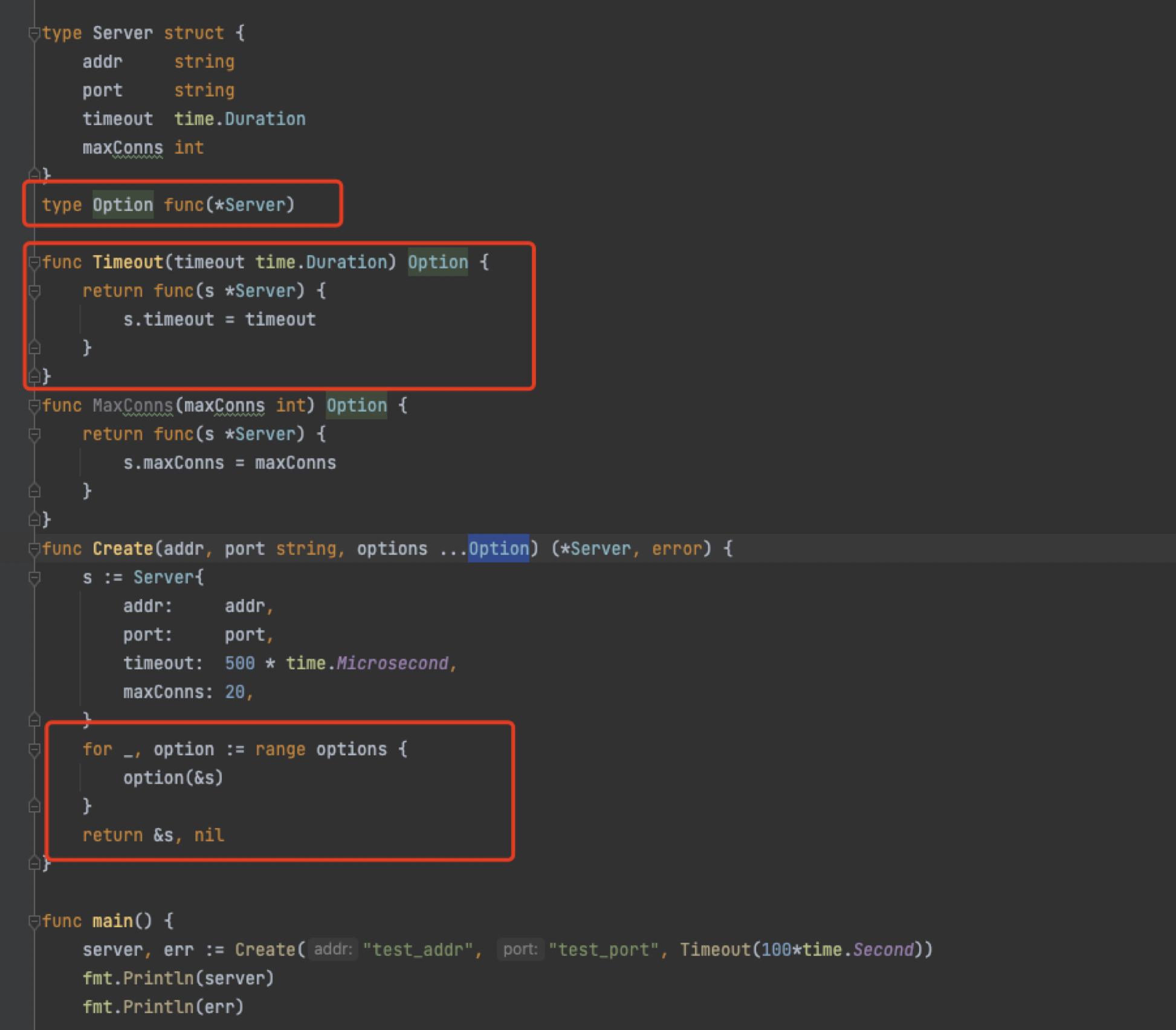
如何优雅的用golang封装配置项(Functional Options)
导读 最近要封装一个公共服务,涉及到配置项的地方总是找不到合理的方案,后来看了一下grpc在配置方面的封装,了解到原来是golang特有的Functional Options编程模式,今天分享给大家,希望你能用到,咱们直接来看…...

Springboot 使用thymeleaf 服务器无法加载resources中的静态资源异常处理
目录一、异常错误二、原因三、解决方法方法1. 将无法编译的静态资源放入可编译目录下方法2. 重新编译项目加载资源方法3. 修改pom.xml资源配置文件方法4. 不连接远程数据库启动,使用本地数据库一、异常错误 Springboot使用thymeleaf,并连接远程数据库启…...

服务端IOS订阅类型支付接入详细说明与注意事项
一、说明 由于本人在开发ios订阅类型支付接入的时候,遇到了很多坑,也查了不少资料,逐步完善了整个ios订阅支付服务端接入的功能,在这里写下总结和一些注意事项的记录,方便未来需要重新接入或者避免一些不必要的坑,这里…...
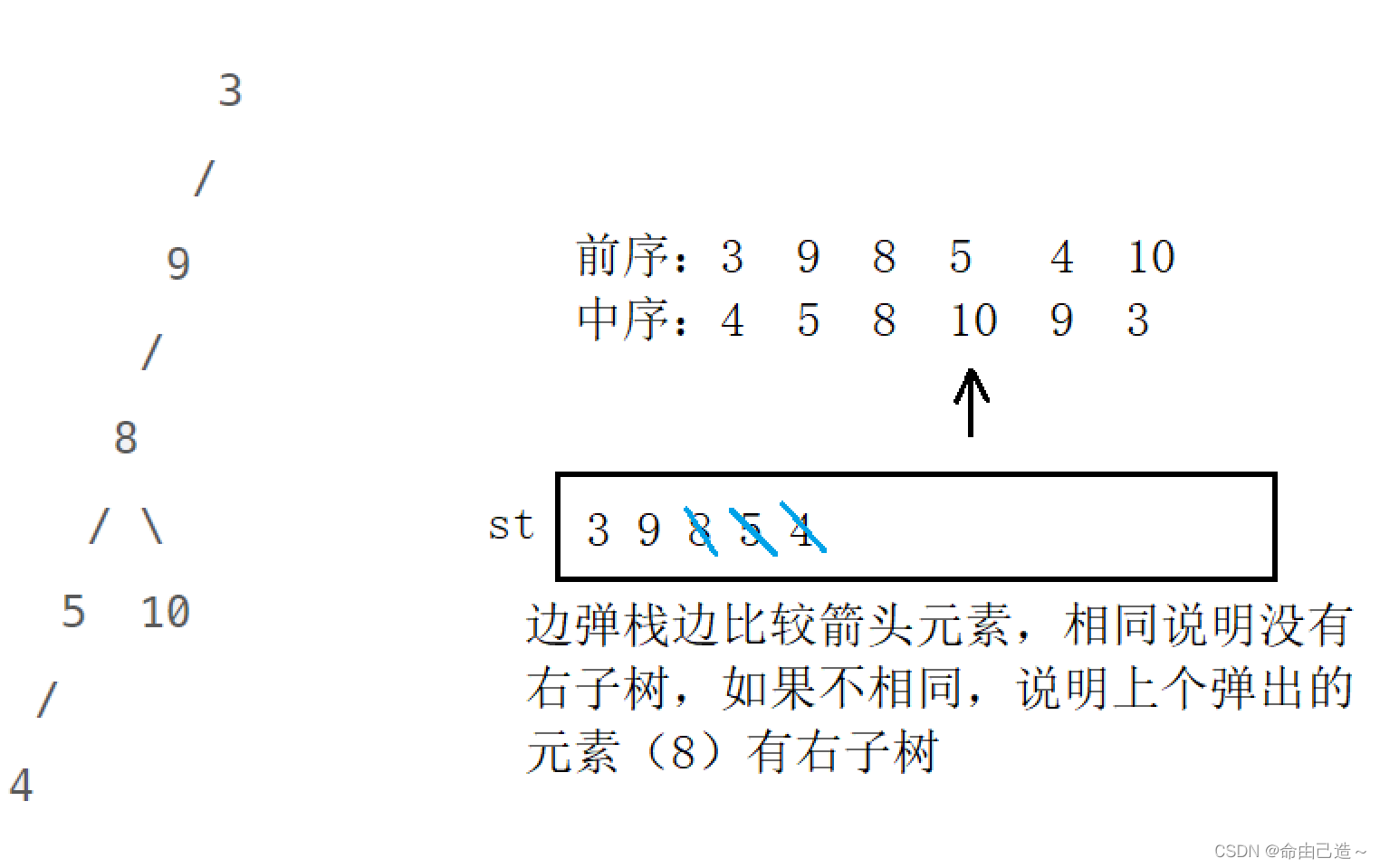
【剑指Offer】重建二叉树(递归+迭代)
重建二叉树一、递归法二、迭代法题目链接 题目描述: 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,…...

注解@Transactional 原理和常见的坑
这篇文章,会先讲述 Transactional 的 4 种不生效的 Case,然后再通过源码解读,分析 Transactional 的执行原理,以及部分 Case 不生效的真正原因1 项目准备下面是 DB 数据和 DB 操作接口:uidunameusex1张三女2陈恒男3楼仔…...

2023年全国最新交安安全员精选真题及答案4
百分百题库提供交安安全员考试试题、交安安全员考试预测题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 31.特种劳动防护用品必须具有“三证”,下列不属于“三证”的是&#…...
扬帆优配|半天翻倍,“蹭热点”翻车,前期“牛股”已近腰斩
周五上午,A股商场整体走低,多数职业板块和个股跌落,军工和核算机等板块逆势上涨,北向资金半天净卖出额约38亿元。 个股方面,昨夜公告被证监会立案查询的奥联电子股价再度大跌,盘中最贱价较近期高位已腰斩。…...

6 种易于上手的编程副业,每月赚取 1,000 多美元——没有废话
没有自由职业者或博客,也不需要前期费用。你们中的大多数人阅读这样的故事是希望其中的一些故事能帮助您赚更多的钱。好吧,几年前我还是同一个人。我希望尝试一些新的副业并赚点钱。其中一个视频建议我在网上写作,此后我写了很多技术文章。在…...
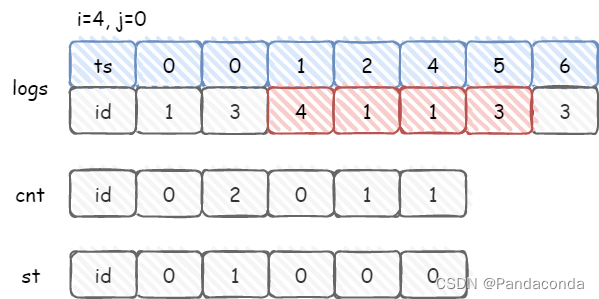
第九届蓝桥杯省赛 C++ B组 - 日志统计
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:蓝桥杯题解集合 📝原题地址:日志统计 📣专栏定位:为想参加蓝桥杯的小伙伴整理常考算法题解,祝大家…...

记一次服务器入侵事件的应急响应
0x01 事件背景 8月某日,客户官网被黑,需在特定时间内完成整改。为避免客户业务受到影响,实验室相关人员第一时间展开本次攻击事件的应急处理。 0x02 事件分析 网站源码被篡改,攻击者一定获取到了权限,那么接下来的思…...
)
作用域链查找机制(回顾)
全局 / 私有变量作用域的概念作用域链 scopeChain 的概念作用域链 scopeChain 的形成函数执行步骤作用域链查找机制 全局 / 私有变量 全局变量:在全局上下文EC(G)中的全局变量对象VO(G)中,存储的变量 私有变量:在函数执行形成的私有上下文EC(XXX)中的变…...

前端基础之HTML扫盲
文章目录一. 第一个HTML程序1. 创建一个HTML文件并运行2. HTML的基本结构二. HTML常见标签1. 注释标签2. 标题标签3. 段落标签4. 换行标签5. 格式化标签6. 图片标签7. 超链接标签8. 表格标签9. 列表标签10. 表单标签10.1 input标签10.2 select标签10.3 textarea标签11. 无语义标…...

大规模食品图像识别:T-PAMI 2023论文解读
美团基础研发平台视觉智能部与中科院计算所展开科研课题合作,共同构建大规模数据集Food2K,并提出渐进式区域增强网络用于食品图像识别,相关研究成果已发表于T-PAMI 2023。本文主要介绍了数据集特点、方法设计、性能对比,以及基于该…...

【java】Spring Cloud --Spring Cloud Alibaba RocketMq 异步通信实现
文章目录介绍RocketMQ特点Spring Cloud StreamWindow搭建部署RocketMQ下载启动NameServer服务启动Broker服务示例创建 RocketMQ 消息生产者创建 RocketMQ 消息消费者使用示例示例关联项目运行示例测试介绍 RocketMQ 是一款开源的分布式消息系统,基于高可用分布式集…...
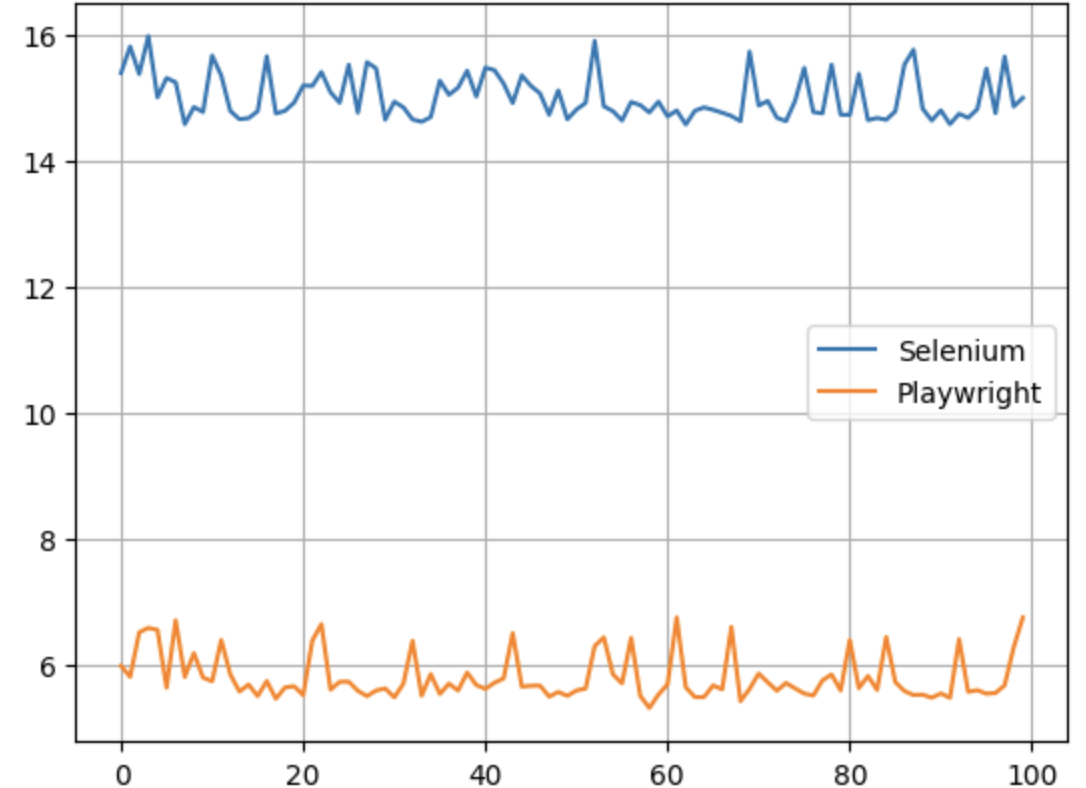
玫瑰花变蚊子血,自动化无痕浏览器对比测试,新贵PlayWright Vs 老牌Selenium,基于Python3.10
也许每一个男子全都有过这样的两个女人,至少两个。娶了红玫瑰,久而久之,红的变了墙上的一抹蚊子血,白的还是床前明月光;娶了白玫瑰,白的便是衣服上沾的一粒饭黏子,红的却是心口上一颗朱砂痣。–…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
