蓝桥杯---第一讲 递归与递推
文章目录
- 前言
- Ⅰ. 递归实现指数型枚举
- 0x00 算法思路
- 0x00 代码书写
- 0x00 思考总结
- Ⅱ. 递归实现排列型枚举
- 0x00 算法思路
- 0x01代码书写
- 0x02 思考总结
- Ⅲ. 简单斐波那契
- 0x00 算法思路
- 0x01 代码书写
- Ⅳ. 费解的开关
- 0x00 算法思路
- 0x01 代码书写
- Ⅴ. 递归实现组合型枚举
- 0x00 算法思路
- 0x01 代码书写
- Ⅵ. 带分数
- 0x00 算法思路
- 0x01 代码书写
- Ⅶ. 飞行员兄弟
- 0x00 算法思路
- 0x01 代码书写
- Ⅷ. 翻硬币
- 0x00 算法思路
- 0x01 代码书写
- 总结
前言
本篇博客主要打卡记录博主学习蓝桥杯C++AB组辅导课的习题第一章节的题目。
Ⅰ. 递归实现指数型枚举
0x00 算法思路
这一道题主要考查 dfs 算法,然后这一道题就是以位置来进行 搜索 当搜索到最后一个位置的时候就可以 收获结果 然后考虑枚举到的位置 可以选择 选 或者 不选
0x00 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 16;int n;
int st[N]; // 状态,记录每个位置当前的状态:0表示还没考虑,1表示选,2表示不选 void dfs(int u)
{if(u > n){for(int i = 1 ; i <= n ; ++ i)if(st[i] == 1)cout << i << " ";cout << endl;return;}//不选st[u] = 2;dfs(u + 1);st[u] = 0; //注意恢复现场 //选st[u] = 1;dfs(u + 1); st[u] = 0; //注意恢复现场}int main()
{ cin >> n;dfs(1); //枚举第一个位置 return 0;
}
0x00 思考总结
这一道题目 就是枚举每一个位置,然后进行选这个数字或者不选这个数字,当枚举到末尾的时候就可以进行收获(打印结果) —> 本质就是枚举每一个位置然后根据选或不选进行的排列组合
Ⅱ. 递归实现排列型枚举
0x00 算法思路
利用一个判断数组st数组,检查是否这个位置的数字我已经使用过了,如果使用过了,就继续,如果没有就直接放到a数组里,递归下一个位置
0x01代码书写
#include<bits/stdc++.h>using namespace std;const int N = 11;int n;
int st[N];//记录这个数字是否被使用过false表示没有,true表示用过
int a[N];//存放数字 方便打印void dfs(int u)
{if(u > n)//(u == n + 1)也是可以的表示枚举到最后一个位置{for(int i = 1 ; i <= n; ++ i)cout << a[i] << " ";cout << endl;return; }for(int i = 1 ; i <= n ; ++ i){if(st[i] == false){a[u] = i;st[i] = true;dfs(u + 1);st[i] = false; //恢复现场}}return;
}int main()
{ cin >> n;dfs(1); //枚举第一个位置 return 0;
}
0x02 思考总结
对比上一道题目,上一道是根据选或不选来进行排列组合,这一道题目则是根据n的位置的多少进行排列组合,这里面用到了一个 st 数组来判断这一个数字是否被使用过,从而对这n个位置的数字进行排列组合
Ⅲ. 简单斐波那契
0x00 算法思路
简单的递推公式问题
0x01 代码书写
#include <iostream>
using namespace std;
int main()
{int n;cin >> n;int a = 0, b = 1;for (int i = 0; i < n; i ++ ){cout << a << ' ';int c = a + b;a = b;b = c;}cout << endl;return 0;
}
Ⅳ. 费解的开关
0x00 算法思路
暴力枚举第一行的32—>2的5次方 种情况,然后去统计第一行的五位01串中出现1的数量然后进行turn和step++,
然后枚举除了最后一行的前面四行,遇到 ‘0’ 就可以对 i + 1 行 j 列 进行 turn 操作,从而使得 i,j 这个位置的灯改变成亮。
最后去横扫最后一行,看是否有黑的灯,如果有的话,代表我们的操作是无法完成任务的,所以 输出-1
当发现没有黑的时候,就可以取最小值进行迭代了。
这里复制粘贴一下Acwing上边的疑惑讲解:
1.高票题解代码中的 if (k >> j & 1) 究竟什么意思?
其中,k保存的根本就不是第一行的灯所有可能的状态,不然它第j位都为1了还按它干嘛? k单纯只是保存了第一行按开关的32种方式,与输入数据无关。
且大多数题解代码中都规定了k在二进制下某位为1就代表我们选择按下这一位所在编号的开关,你也可以自己规定k在二进制下某位为0才代表我们选择按下这一位所在编号的开关,这都无所谓。
比如k在二进制下表示为10001,就代表我们选择按第一行编号为0和编号为4的开关,然后对输入数据中第一行这两位执行turn操作。
贴一个Acwing大佬写的超级详细的题解
AcWing 95. 费解的开关(有图超详细,看不懂揍我)
0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 6;char g[N][N], backup[N][N];
int dx[5] = {-1,0,1,0,0}, dy[5] = {0,1,0,-1,0};void turn(int x,int y)//dfs--->迷宫类模板
{for(int i = 0 ; i < 5 ; ++ i){int a = x + dx[i], b = y + dy[i];if(a < 0 || a >= 5 || b < 0 || b >= 5) continue;g[a][b] ^= 1;}
}int main()
{ int T;cin >> T;while(T -- ){for(int i = 0 ; i < 5 ; ++ i)for(int j = 0 ; j < 5 ; ++ j)cin >> g[i][j];int res = 10;for(int op = 0 ; op < 32 ; ++ op){memcpy(backup, g , sizeof g);int step = 0;for(int i = 0 ; i < 5 ; ++ i)if(op >> i & 1){step ++;turn(0, i);}for(int i = 0 ; i < 4 ; ++ i)for(int j = 0 ; j < 5 ; ++ j)//对黑的灯进行turn操作if(g[i][j] == '0'){step ++;turn(i + 1 , j);}bool dark = false;for(int i = 0 ; i < 5 ; ++ i)//遍历最后一行看是否存在黑着的灯if(g[4][i] == '0'){dark = true;break;}if(!dark) res = min(res,step);memcpy(g, backup, sizeof g);}if(res > 6) res = -1;cout << res << endl;}return 0;
}
Ⅴ. 递归实现组合型枚举
0x00 算法思路
通过枚举第一个位置和开始的数进行dfs操作,当搜索到最后一个位置的时候就可以收获结果了
0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 30;int n, m;
int st[N];void dfs(int u, int start)
{if(u == m + 1){for(int i = 1 ; i <= m ; ++ i)cout << st[i] << " ";cout << endl;return; }for(int i = start ; i <= n ; ++ i){st[u] = i;dfs(u + 1, i + 1);st[u] = 0;}
}int main()
{ cin >> n >> m;dfs(1, 1); //枚举第一个位置 return 0;
}
Ⅵ. 带分数
0x00 算法思路
根据 n = a + b / c 变换 成为 : cn = ac + n所以可以先确定ac的值进而确定b的值所以有以下思路:
- 枚举a的数值
- 枚举c的数值
- 判断b是否符合条件
这个题目也用到了全排列的思想—>本节的第二道题目就是全排列题目的代码和思路
0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 10;int n;
bool st[N],backup[N];
int ans;bool check(int a,int c)
{long long b = n * (long long)c - a * c;//防止溢出用long longmemcpy(backup,st,sizeof st);//用备份操作if(!a || !b || !c) return false;while(b)//判断b当中的数字是否被使用过了已经{int x = b % 10;b /= 10;if(!x || backup[x]) return false;//被使用过了就返回falsebackup[x] = true;}for(int i = 1 ; i <= 9 ; ++ i)//最后再对abc三个数字所选的数字看看是否选完了0~9个数字if(!backup[i])return false;return true;
}void dfs_c(int u, int a ,int c)
{if(u > 9) return; //超过9个数就可以returnif(check(a,c)) ans ++; //发现组合就可以 ++ansfor(int i = 1 ; i <= 9 ; ++ i)//去确定c的值{if(!st[i]){st[i] = true;dfs_c(u + 1,a, c * 10 + i);st[i] = false;}}
}void dfs_a(int u , int a)
{if(a >= n) return; //a不能大于nif(a) dfs_c(u,a,0);//a不能是0 然后去找cfor(int i = 1 ; i <= 9 ; ++ i)//去确定a的值{if(!st[i]){st[i] = true;dfs_a(u + 1,a * 10 + i);st[i] = false;}}return;
}int main()
{cin >> n;dfs_a(0, 0);// 去递归搜索 a 一开始选0个数字(用了多少个数),a是0。cout << ans << endl;return 0;
}
Ⅶ. 飞行员兄弟
0x00 算法思路
先说结论,在判断是否要对(i, j)位置的把手进行切换时,只需要计算一下第i行和第j列总共7个把手(以下称为(i, j)对应的十字)中闭合的把手数目,如果是奇数个就进行切换,偶数个就不进行切换。(奇数个是该位置的把手进行过切换的充要条件)
因此我们从上到下从左到右顺次的对16个把手进行上述判断。如果判断结果是奇数个那么说明该位置被切换过,进行记录即可。
0x01 代码书写
#include<bits/stdc++.h>using namespace std;#define x first
#define y secondconst int N = 5;
typedef pair<int,int> PII;
char g[N][N], backup[N][N];int get(int x, int y)
{return x * 4 + y;
}void turn_one(int x, int y)
{if (g[x][y] == '+') g[x][y] = '-';else g[x][y] = '+';
}void turn_all(int x, int y)
{for (int i = 0; i < 4; i ++ ){turn_one(x, i);turn_one(i, y);}turn_one(x, y);
}int main()
{for(int i = 0 ; i < 4 ; ++ i) cin >> g[i];vector<PII> res;for(int op = 0 ; op < 1 << 16 ; ++ op){vector<PII> temp;memcpy(backup, g ,sizeof g);for(int i = 0 ; i < 4 ; ++ i)for(int j = 0 ; j < 4 ; ++ j){if(op >> get(i, j) & 1){temp.push_back({i, j});turn_all(i, j);}}bool has_closed = false;for(int i = 0 ; i < 4 ; ++ i)for(int j = 0 ; j < 4 ; ++ j){if(g[i][j] == '+')has_closed = true;}if(has_closed == false) if(res.empty() || res.size() > temp.size()) res = temp;memcpy(g,backup,sizeof g);}cout << res.size() << endl;for(auto& op : res) cout << op.x + 1 << " " << op.y + 1 << endl;return 0;
}
Ⅷ. 翻硬币
0x00 算法思路
将硬币和目标的样子进行比较,当发现不一样的时候就进行 turn 翻转即可
0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N=110;
char start[N], aim[N];
int n;void turn(int i)
{if(start[i]=='o') start[i]='*';else start[i]='o';
}int main()
{cin >> start >> aim;n = strlen(start);int res=0;for(int i = 0; i < n - 1 ; i ++){if(start[i] != aim[i]){turn(i), turn(i+1);res ++;}}cout << res << endl;return 0;
}
总结
本篇博客主要讲解了递推与递归的算法,也涉及到了 dfs 搜索算法的使用,其实 dfs 算法可以
- 先去想dfs的含义,参数的含义
- 找到dfs的结束条件进行收获结果
- 根据题目要求实现dfs代码
希望自己可以多多练习,后面蓝桥杯辅导课看完就会去看算法提高课继续提升
相关文章:

蓝桥杯---第一讲 递归与递推
文章目录 前言Ⅰ. 递归实现指数型枚举0x00 算法思路0x00 代码书写0x00 思考总结 Ⅱ. 递归实现排列型枚举0x00 算法思路0x01代码书写0x02 思考总结 Ⅲ. 简单斐波那契0x00 算法思路0x01 代码书写 Ⅳ. 费解的开关0x00 算法思路0x01 代码书写 Ⅴ. 递归实现组合型枚举0x00 算法思路0…...
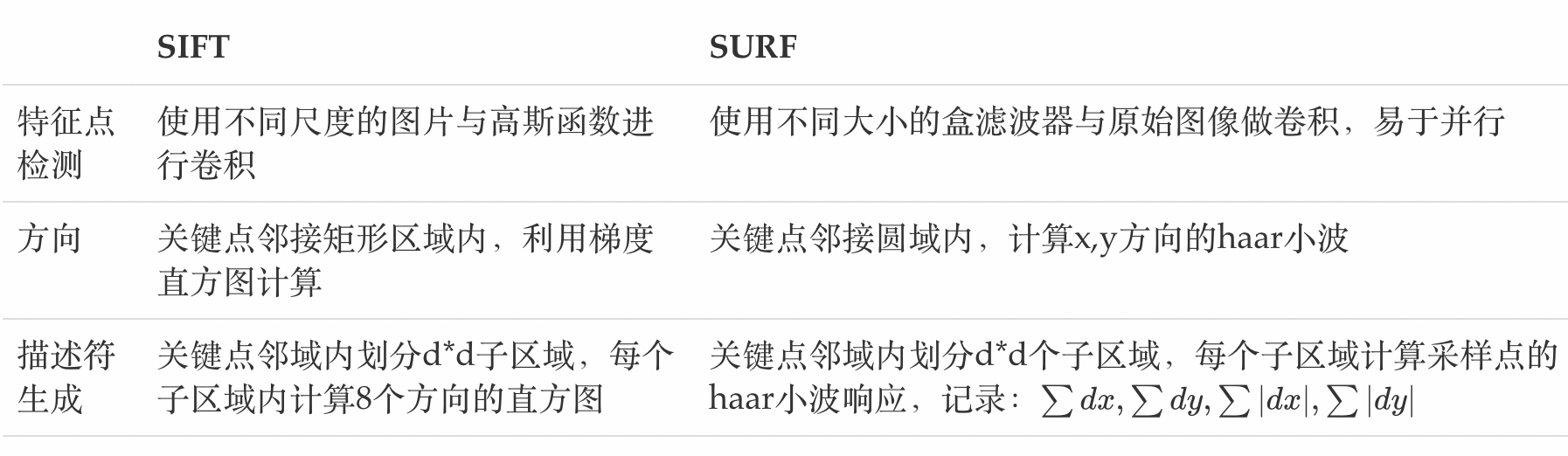
OpenCV 15(SIFT/SURF算法)
一、SIFT Harris和Shi-Tomasi角点检测算法,这两种算法具有旋转不变性,但不具有尺度不变性,以下图为例,在左侧小图中可以检测到角点,但是图像被放大后,在使用同样的窗口,就检测不到角点了。 尺度…...
)
前端二维码图片解析图片识别/网络图片解析成链接/图片网络链接转本地链接(Js/Vue/Jquery)
注:需要用到canvas/jsqr/jquery! 1、远程图片链接本地化 页面: <!-- 识别二维码用的 canvas--> <canvas class"canvas" ref"canvas" style"display: none"></canvas> 1.创建图片 get2: fu…...
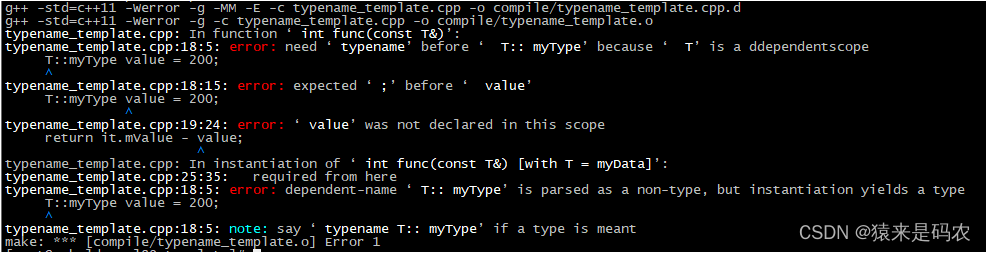
模板中的依赖类型使用 --- typename
依赖类型,顾名思义就是依赖于模板参数的类型,在使用这种类型时,必须使用 typename,否则编译器是无法知道是在使用类型,还是类的成员(因为类的静态成员的使用方法也是T::xxx,这跟某个类中的类型的…...
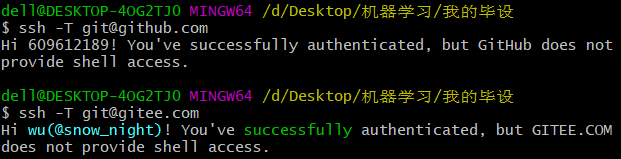
git 同时配置 gitee github
git 同时配置 gitee github 1、 删除C:\Users\dell\.ssh目录。 在任意目录右击——》Git Bash Here,打开Git Bash窗口,下方命令在Git Bash窗口输入。 2、添加git全局范围的用户名和邮箱 git config --global user.email "609612189qq.com" …...

2023.10.8 面试
面试工作1年的程序员 看到生涩才入职场不久的面试者,为人也相对诚恳的模样,我对此是很欣赏的态度。 因为完全看到了自己毕业1年时的场景。 简历上写的事情,讨论起来,描述不清楚,为此感到遗憾,因我本人也会…...

【前端】js实现队列功能 先进后出 先进先出 等
也可以定义一个定时器 不断的去取队列 执行任务 用一个flag定义队列正在执行中, 如果没有执行 则定时器不断的去调用队列,(因为会随时添加一个任务到队列中) 队列任务结束后 自动取下一个队列 也可以边加队列 边取 队列定义 function Queue() {//初始化队列(使用…...

07.数据持久化之文件操作
1. 文件操作 计算机的文件,就是存储在某种 长期储存设备 上的一段 数据 长期存储设备包括:硬盘、U 盘、移动硬盘、光盘… 文本文件和二进制文件 文本文件 可以使用 文本编辑软件 查看本质上还是二进制文件例如:python 的源程序 二进制文件…...
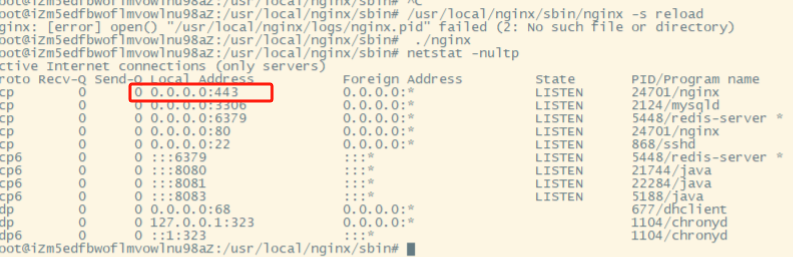
nginx开启https配置之后网页无法访问问题处理
背景说明 最近新购服务器部署nginx之后按照之前的方式部署前端项目并配置https之后访问页面显示:无法访问.新的服务器ECS系统和之前相同,nginx安装方式也相同,nginx配置方式也是相同.但是访问还是显示无法访问.下面简单记录一下问题处理过程. 处理过程 1.https访问之后无法访问…...
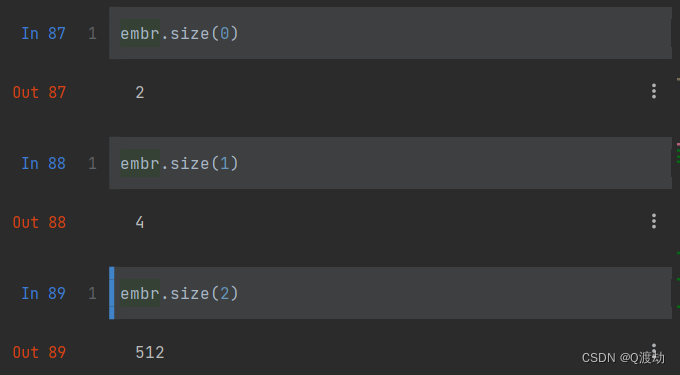
文本嵌入层
目录 1、文本嵌入层的作用 2、代码演示 3、构建Embeddings类来实现文本嵌入层 1、文本嵌入层的作用 无论是源文本嵌入层还是目标文本嵌入,都是为了将文本词汇中的数字表示转变为向量表示,希望在这样的高维空间中捕捉词汇之间的关系 2、代码演示 Emb…...
如何搭建自动化测试框架
关于测试框架的好处,比如快速回归提高测试效率,提高测试覆盖率等这里就不讨论了。这里主要讨论自动化框架包含哪些内容,以及如何去设计一个测试框架。 1. 什么是自动化测试框架? 它是由一个或多个自动化测试基础模块、自动化测试…...
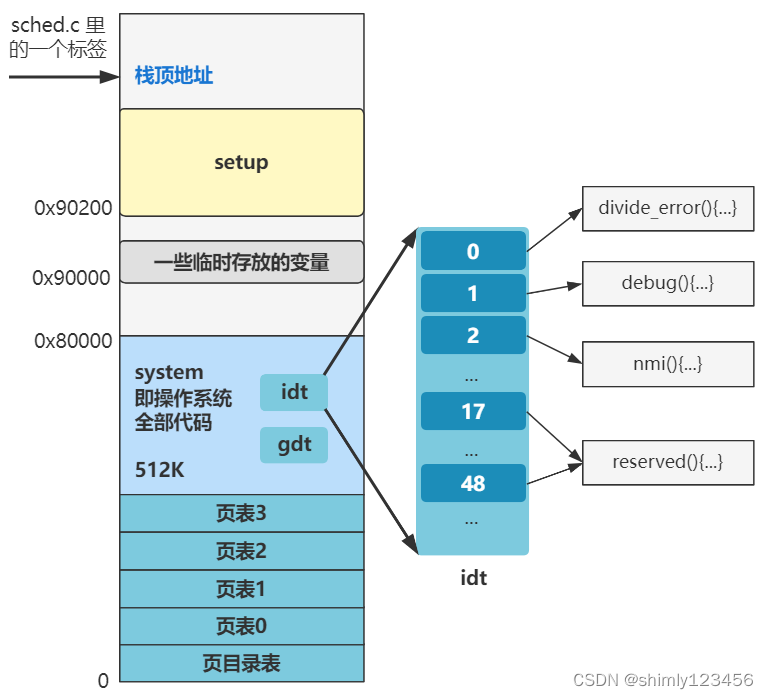
抄写Linux源码(Day17:你的键盘是什么时候生效的?)
回忆我们需要做的事情: 为了支持 shell 程序的执行,我们需要提供: 1.缺页中断(不理解为什么要这个东西,只是闪客说需要,后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的,所以需要这两个东…...

在原生html中使用less
引入less <link rel"stylesheet/less" href"./lessDemo.less" /><script src"./js/less.min.js"></script> less.min.js文件下载地址:https://github.com/less/less.js 注意:less文件在前,js文件在后…...
【Qt】顶层窗口和普通窗口区别以及用法
区别 在Qt项目开发中,经常会用到窗体控件用于显示及数据操作和其他交互等。 但,窗体分为顶层窗口(Top-level Window)和普通窗口(Regular Window)。 他们之间是有区别的,包括在项目实际中的用法…...
qt开发从入门到实战2
以下是本人学习笔记 原视频:最新QT从入门到实战完整版|传智教育 qt开发从入门到实战1 练习示例 设计一个按钮,点击时弹出新窗口,再次点击时新窗口关闭 // exerciseQWidget* second_window new QWidget();QPushButton* btn3 new QPushBu…...
Android---字节码层面分析Class类文件
Java 提供了一种可以在所有平台上都能使用的一种中间代码---字节码文件(.class文件)。有了字节码,无论是那个平台只要安装了虚拟机都可以直接运行字节码文件。有了虚拟机,解除了 java 虚拟机与 java 代码之间的耦合。 Java 虚拟机当初被设计出来时就不单…...
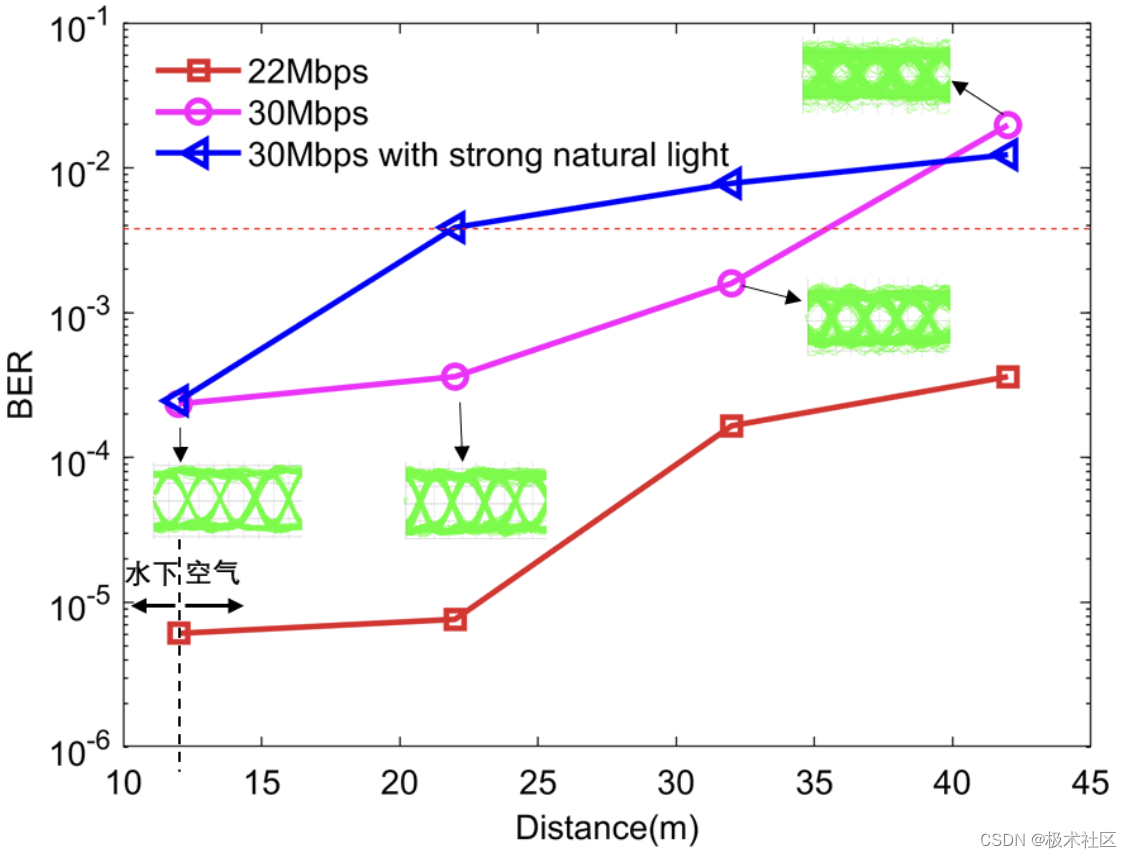
【2023研电赛】东北赛区一等奖作品:基于FPGA的小型水下无线光通信端机设计
本文为2023年第十八届中国研究生电子设计竞赛东北赛区一等奖作品分享,参加极术社区的【有奖活动】分享2023研电赛作品扩大影响力,更有丰富电子礼品等你来领!,分享2023研电赛作品扩大影响力,更有丰富电子礼品等你来领&a…...

JWT授权为啥要在 Authorization标头里加个Bearer 呢
这是因为 W3C 的 HTTP 1.0 规范,Authorization 的格式是: Authorization: <type> <authorization-parameters> w3c规定,请求头Authorization用于验证用户身份。这就是告诉我们,token应该写在请求头Authorization中 …...

一篇理解TCP协议
一、TCP协议概念。 TCP(Transmission Control Protocol,传输控制协议)是一种面向连接的、可靠的传输层协议。它主要用于在计算机网络中,通过建立可靠的通信连接来进行数据传输。 TCP协议的特点如下: 可靠性…...

rk平台android12系统设置里面互联网选项中的以太网选项点击不了问题
rk平台android12系统中,系统设置中的互联网选项,当连接以太网以后,会显示以太网的选项,但是点击没作用,现在需要点击能够进入到以太网的设置界面,需要添加相关的点击事件。 首先,在packages/apps/Settings/AndroidManifest.xml中的以太网设置配置添加一个action,用于打…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
