cv2.split函数与cv2.merge函数
split函数用于图像BGR通道的分离
merge函数用于可将分开的图像通道合并到一起
1.split函数的使用

这是原图,我们使用split函数对其三个通道进行分离。
注意:split函数分离通道的顺序是B、G、R。
以下方法是将三个通道的值都设置为与某一个通道相同。
import numpy as np
import cv2 # 导入opencv模块image = cv2.imread("test.jpg") # 读取要处理的图片
B, G, R = cv2.split(image) # 分离出图片的B,R,G颜色通道
cv2.imshow("RED COMPONENT FOR ALL THREE CHANNELS", R) # 显示三通道的值都为R值时的图片
cv2.imshow("GREEN COMPONENT FOR ALL THREE CHANNELS", G) # 显示三通道的值都为G值时的图片
cv2.imshow("BLUE COMPONENT FOR ALL THREE CHANNELS", B) # 显示三通道的值都为B值时的图片
cv2.waitKey(0)B通道

G通道

R通道

如果图中某一颜色较强,这种方法可以用于区分出图中B、G、R三原色的强弱。
如果想提取单一通道,其他通道值设为0,使用以下代码:
import numpy as np
import cv2 # 导入opencv模块image = cv2.imread("test.jpg") # 读取要处理的图片
B, G, R = cv2.split(image) # 分离出图片的B,R,G颜色通道
zeros = np.zeros(image.shape[:2], dtype="uint8") # 创建与image相同大小的零矩阵
cv2.imshow("DISPLAY BLUE COMPONENT", cv2.merge([B, zeros, zeros])) # 显示(B,0,0)图像
cv2.imshow("DISPLAY GREEN COMPONENT", cv2.merge([zeros, G, zeros])) # 显示(0,G,0)图像
cv2.imshow("DISPLAY RED COMPONENT", cv2.merge([zeros, zeros, R])) # 显示(0,0,R)图像
cv2.waitKey(0)代码中使用了image.shape[:2],理解image.shape[:2]可参考下文。理解image.shape[:2]与image.shape[:3]![]() https://blog.csdn.net/Mr_LanGX/article/details/120275615
https://blog.csdn.net/Mr_LanGX/article/details/120275615
例:h,w = img.shape[:2] 获取彩色图片的高、宽,并且赋值给h和w;如果是h,w,v = img.shape[:3] 获取彩色图片的高、宽、通道,并赋值给h w v
运行代码:
B通道

G通道

R通道

2.merge函数的使用
merge函数将三个分离的通道合并。
import numpy as np
import cv2 # 导入opencv模块image = cv2.imread("test.jpg") # 读取要处理的图片
B, G, R = cv2.split(image) # 分离出图片的B,R,G颜色通道
cv2.imshow("MERGE RED,GREEN AND BLUE CHANNELS", cv2.merge([B, G, R])) # 显示(B,G,R)图像
cv2.waitKey(0)显示图像与原图相同。
相关文章:

cv2.split函数与cv2.merge函数
split函数用于图像BGR通道的分离 merge函数用于可将分开的图像通道合并到一起 1.split函数的使用 这是原图,我们使用split函数对其三个通道进行分离。 注意:split函数分离通道的顺序是B、G、R。 以下方法是将三个通道的值都设置为与某一个通道相同。…...
)
Vue--1.7watch侦听器(监视器)
作用:监视数据变化,执行一些业务逻辑或异步操作。 语法: 1.简单写法->简单类型数据,直接监视 const app new Vue({el: #app,data: {words:},watch:{words(newValue,oldValue){}}}) const app new Vue({el: #app,data: {obj…...

序列:全序关系
一个序列满足全序关系必须满足以下条件: 反对称性:若 a ≤ b a\le b a≤b,则 b ≥ a b\ge a b≥a传递性:若 a ≤ b a\le b a≤b 且 b ≤ c b\le c b≤c,则 a ≤ c a\le c a≤c完全性: a ≤ b a\le b …...

100M服务器能同时容纳多少人访问?
100M的服务器带宽能够同时容纳的用户访问量需要考虑以下几个关键因素: 👉1.单个用户的平均访问流量大小 这取决于网站内容,是否有多媒体等。一般文本类网站每用户每次访问在50-100KB。 👉2.每个用户的平均访问页面 通常每次访问会打开多个页面 &…...
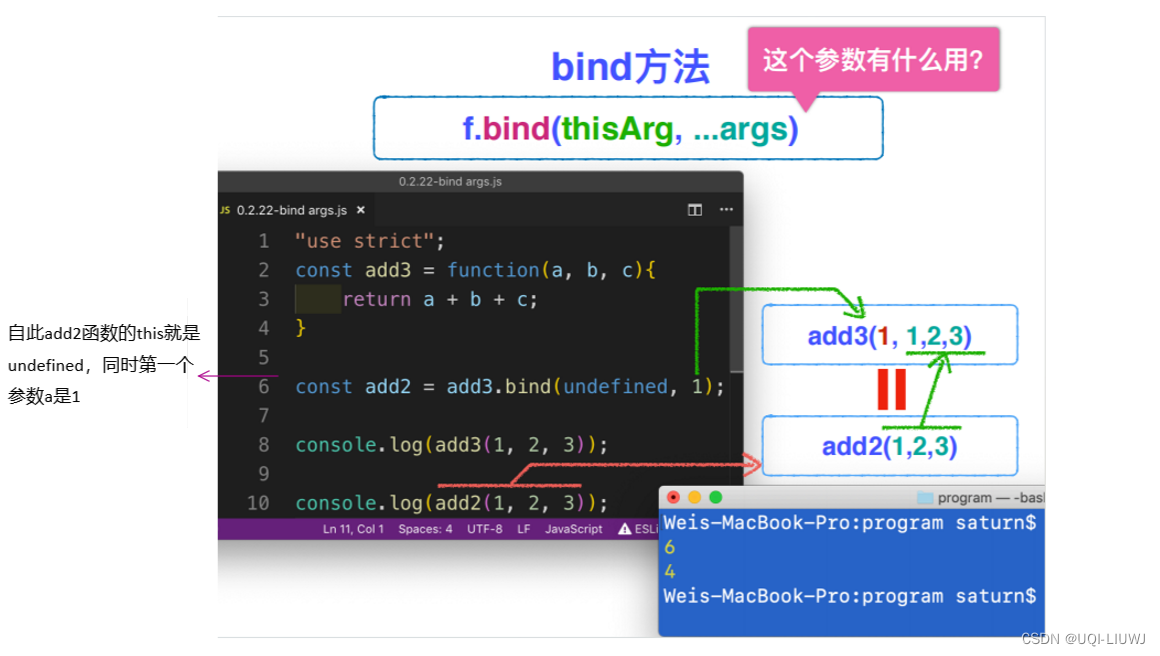
Javascript 笔记:函数调用与函数上下文
在 JavaScript 中,函数上下文通常指的是函数在执行时的当前对象的引用,这通常用 this 关键字表示。this 关键字在不同的执行上下文中可能引用到不同的对象。 1 全局上下文 当 this 关键字用在全局上下文(不在任何函数内部)&#…...
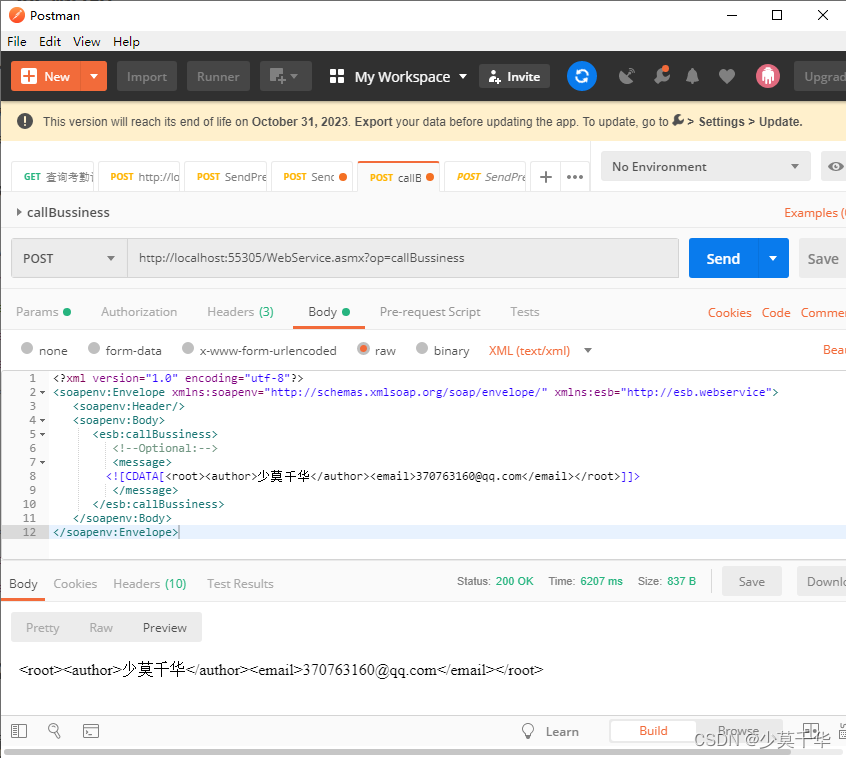
【WebService】C#搭建的标准WebService接口,在使ESB模版作为参数无法获取参数数据
一、问题说明 1.1 问题描述 使用C# 搭建WebService接口,并按照ESB平台人员的要求,将命名空间改为"http://esb.webservice",使用PostmanESB平台人员提供的入参示例进行测试时,callBussiness接口参数message始终为null。 以下是ES…...

Sqlserver关于tempdb临时数据库文件个数的最佳实践
官方文档 https://learn.microsoft.com/zh-cn/sql/relational-databases/databases/tempdb-database?viewsql-server-ver16 https://learn.microsoft.com/en-US/troubleshoot/sql/database-engine/performance/recommendations-reduce-allocation-contention 一般而言&#x…...
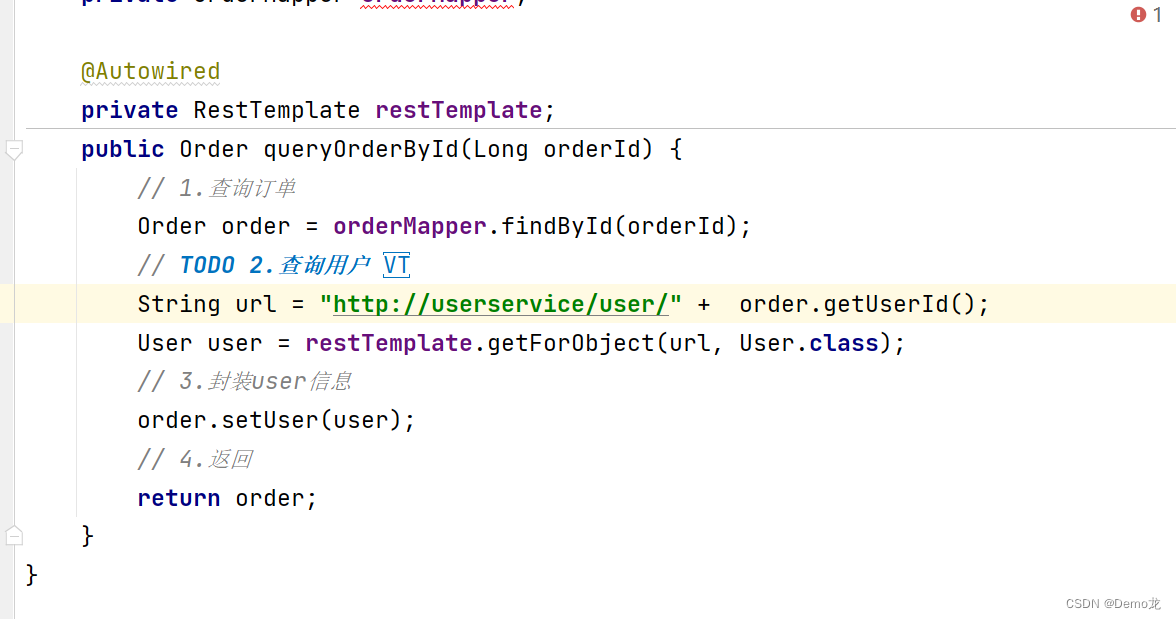
【Java】微服务——微服务介绍和Eureka注册中心
目录 1.微服务介绍2.服务拆分和远程调用2.1.提供者与消费者 3.Eureka注册中心3.1.Eureka的结构和作用3.2.Eureka的结构3.3.搭建Eureka服务3.3.1.引入eureka依赖3.3.2.编写配置文件 3.4.服务注册及拉1)引入依赖2)配置文件3)启动多个user-servi…...

C++ virtual 虚函数 虚基类
https://blog.csdn.net/xbb123456rt/article/details/81986691 基类指针可以指向一个派生类对象,但派生类指针不能指向基类对象。 可以在基类中将被重写的成员函数设置为虚函数,其含义是:当通过基类的指针或者引用调用该成员函数时…...
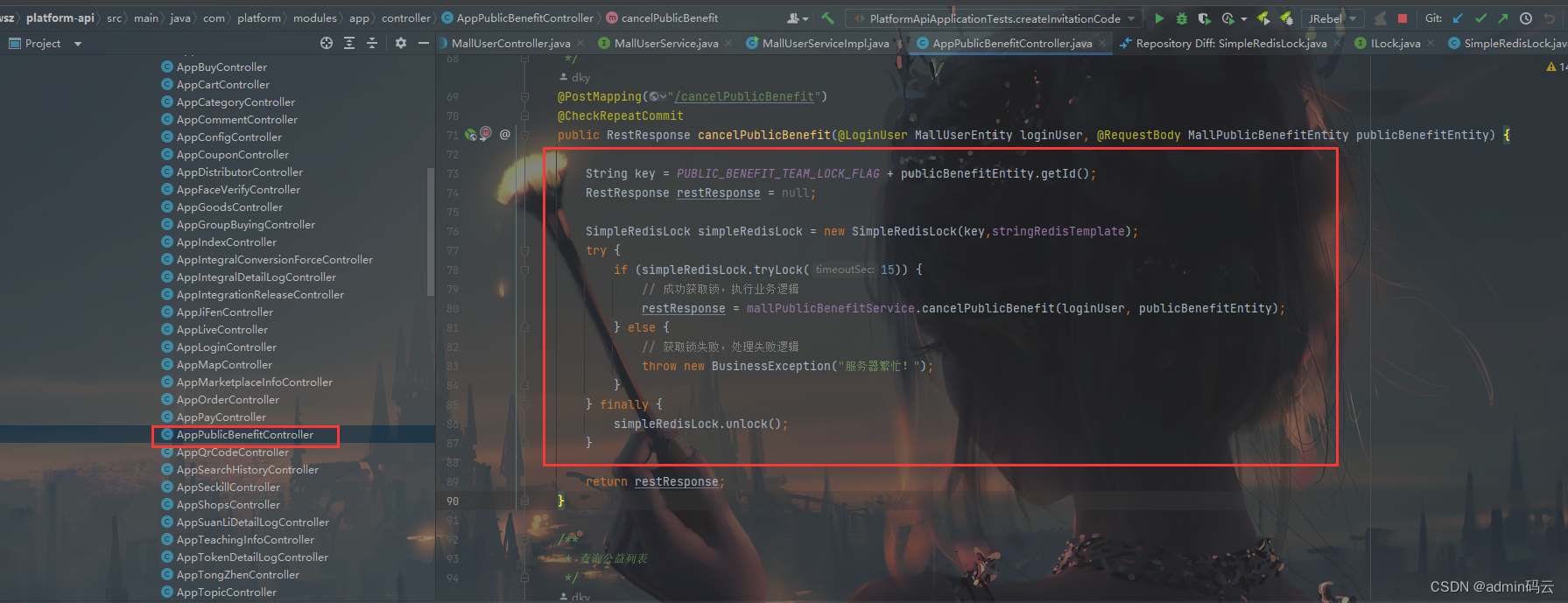
redis分布式秒杀锁
-- 获取锁标识,是否与当前线程一致? if(redis.call(get, KEYS[1]) ARGV[1]) then-- 一致,删除return redis.call(del, KEYS[1]) end -- 不一致,直接返回 return 0package com.platform.lock;public interface ILock {/*** 获取锁…...

【Redis】String内部编码方式
String内部编码方式 int: 8个字节的长整型embstr: 小于等于39个字节的字符串raw: 大于39个字节的字符串...
川西旅游网系统-前后端分离(前台vue 后台element UI,后端servlet)
前台:tour_forword: 川西旅游网前端----前台 (gitee.com) 后台:tour_back: 川西旅游网-------后台 (gitee.com) 后端 :tour: 川西旅游网------后端 (gitee.com)...

Paddle使用pyinstaller打包出错的解决方法
使用PyQt5开发了一个基于paddle ocr的文字识别程序,打包的时候报错了。给大家分享一下解决方法https://juejin.cn/post/7287562282669883451 为了测试paddle模块的打包问题,所以当前demo.py只引用了paddleOCR模块demo.py from paddleocr import PaddleO…...

【Java acm】特殊输入
input: [[1,2,3 ], [4, 5,6], [7,8]] output: [[1, 2, 3], [4, 5, 6], [7, 8]] 思路 按行读入, 然后进行字符串处理, 将其他字符替换为空字符.在split(,) repalceAll(“\s”,“”), 将所有空白字符替换成空字符(包括空格, 制表, 换行等) 代码实现 import java.util.*;publ…...
在Ubuntu 20.04搭建最小实验环境
sudo apt-get -y install --no-install-recommends wget gnupg ca-certificates安装导入GPG公钥所需的依赖包。 sudo wget -O - https://openresty.org/package/pubkey.gpg | sudo apt-key add -导入GPG密钥。 sudo apt-get -y install --no-install-recommends software-p…...

使用uwsgi部署Flask
安装 这里直接使用包管理器提供的版本,不过建议大家使用pip来安装,会少一些坑: (Debian/Ubuntu) apt-get install uwsgi uwsgi-plugin-python3 或使用pip安装: pip3 install uwsgi 试试看 [demo.py] from flask import Flas…...

Android平台实现lottie动画
1、lottie动画简介 Lottie 是一个应用十分广泛动画库,适用于Android、iOS、Web、ReactNative、Windows的库,它解析了用Bodymovin导出为json的Adobe After Effects动画,并在移动和网络上进行了原生渲染。它提供了一套完整得从AE到各个终端的…...

JAVA练习百题之求矩阵对角线之和
题目:求一个3*3矩阵对角线元素之和 程序分析 求一个3x3矩阵的对角线元素之和,我们需要将矩阵的左上到右下以及左下到右上两条对角线上的元素相加。 一个3x3矩阵如下所示: 1 2 3 4 5 6 7 8 9左上到右下的对角线元素和为1 5 9 15&…...

MEM备考打卡
今天是2023.10.9距离考试还有75天 三年前就想考MEM每次总是有各种原因最后选择了放弃,没时间、自制力差、害怕失败。。。。放弃后确还是会想如果自己当时没有放弃是不是就能考上,所以这次不管能不能考上拼搏75天,不能总是停留在想象。加油&a…...

短视频矩阵源码开发部署---技术解析
一、短视频SEO源码搜索技术需要考虑以下几点: 1. 关键词优化:通过研究目标受众的搜索习惯,选择合适的关键词,并在标题、描述、标签等元素中进行优化,提高视频的搜索排名。 2. 内容质量:优质、有吸引力的内…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
