第三章 栈、队列和数组
第三章 栈、队列、数组
- 栈
- 栈的基本概念
- 栈的顺序实现
- 栈的链接实现
- 栈的简单应用和递归
- 队列
- 队列的基本概念
- 队列的顺序实现
- 队列的链接实现
- 数组
- 数组的逻辑结构和基本运算
- 数组的存储结构
- 矩阵的压缩存储
- 小试牛刀
栈和队列可以看作是特殊的线性表,是运算受限的线性表
栈
栈的基本概念
- 栈是运算受限的线性表,插入和删除运算限定在表的某一端进行,允许进行插入和删除的一端为栈桥顶,另一端为栈底。不含任何数据元素的栈为空栈
- 栈的修改原则是后进先出
栈的顺序实现
- 栈的顺序存储结构是用一组连续的存储单元依次存放栈中的每个元素,并用始端做为栈底
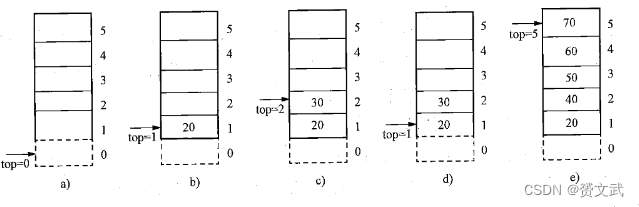
注:进栈操作可以 如下表示:Push(栈名,进栈元素);出栈操作可以如下表示:Pop(栈名,出栈元素)
- 初始化
int InitStack(SeqStk *stk)
{
stk——>top=0;
return 1;
}
- 判栈空
int EmptyStack(SeqStk *stk)
//若栈为空,则返回1,否则返回0
{
if (stk->top==0)return 1;
else return 0;
}
- 进栈
int Push(SeqStk *stk,DataType x)
{
IF (stk->top==maxsize-1){error("栈已满");return 0;}
else { stk->top++; //栈未满,top+1stk->data[stk->top]=x; //元素x进栈return 1;}
}
- 出栈
int Pop(SeqStk *stk)
{if {EmptyStack(stk){error("下溢");return 0;}else{stk->top--;return 1;}
}
- 取栈顶元素
DataType GetTop(SeqStk *stk)
{ if(EmptyStack(stk)) return NULLData;elsereturn stk->data[stk->top];
}
- 双栈(两个栈头对头放数组两端)
const int max=40;
typedef struct Dbstack
{
DataType data[max];
int top1,top2;
}DbStk;
注:双栈判断上溢为top1+1=top2;判栈空为top1=0时,栈1为空;top2=max-1时栈2为空
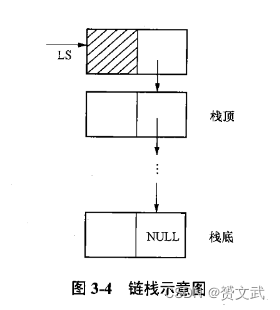
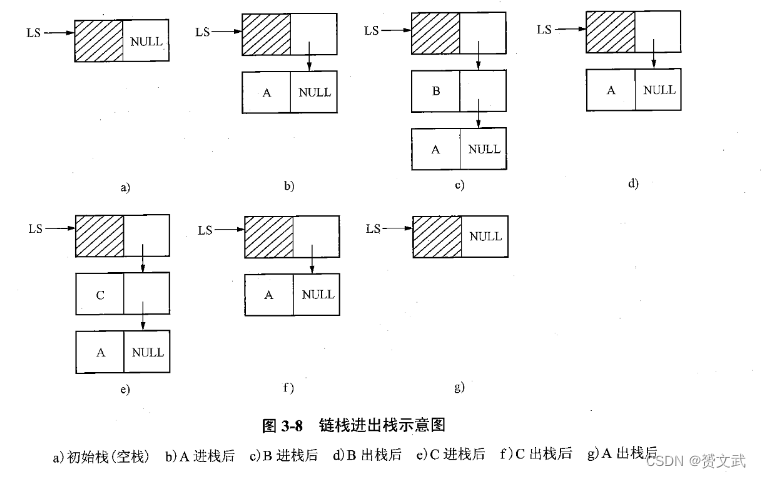
栈的链接实现
- 栈的链接实现称为链栈,链栈可以用带头结点的单链表实现,每个结点空间动态分配,不用预先考虑容量大小
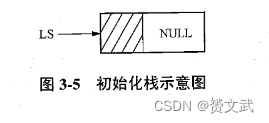
- 初始化
void InitStack(LkStk *LS)
{
LS=(LkStk *)malloc(sizeof(LkStk));
LS->next=Null;
}
- 判栈空
int EmptyStack(LkStk *LS)
//若栈为空则返回值为1,否则返回0
{
if(LS->next==NULL)retun 1;
elsereturn 0;
}
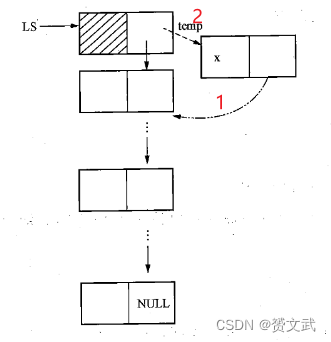
- 进栈
void Push(LkStk *LS,DataType x)
{
LkStk *temp;
temp=(LkStk *)mallloc(sizeof(LkStk)); //temp指向申请的新结点
temp->data=x; //新结点的data域赋值为x
temp->next=LS->next; //temp的next域指向原来栈顶结点
LS->next=temp; //指向新的栈顶结点
}
- 出栈
int Pop(LkStk *LS)
//栈顶元素通过参数返回,直接后继成为新栈顶
{
LkStk *temp;
if(!EmptyStack(LS)){temp=LS->next; //temp指向栈顶结点LS->next=temp->next; //原栈顶的下一个结点成为新栈顶free(temp); //释放原栈顶结点空间return 1;}else rturn 0;
}
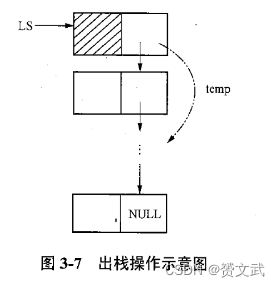
- 取栈顶元素
DataType GetTop(LkStk *LS)
{
if (!EmptyStack(LS))return LS->next->data; //若栈为非空,返回栈顶数据元素
elsereturn NULLData; //返回空元素
}
栈的简单应用和递归
- 如果在一个函数或数据结构的定义中又应用了它自身,那么这个函数或数据结构称为递归定义的
- 递归定义必须同时满足以下两个条件
- 被定义项在定义中的应用具有更小的“规模”
- 被定义项在最小“规模”上的定义是非递归的
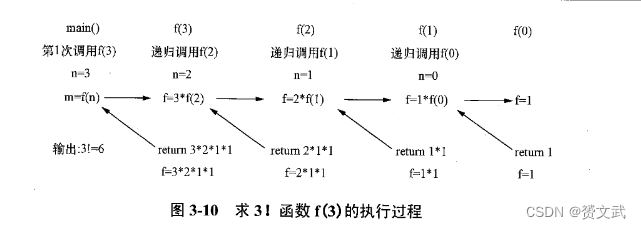
//求3的阶乘
#include<stdio.h>
long f(int n){if(n==0) return 1;elsereturn n*f(n-1);
}
main(){
int m,n=3;
m=f(n);
printf("%d!=%d\n",n,m)
}
队列
队列的基本概念
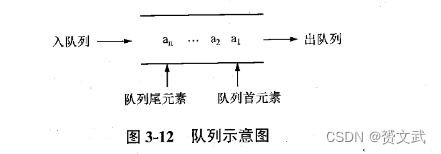
- 队列是有限个同类型数据元素的线性序列,是一种先进先出的线性表(“排队”)
队列的顺序实现
- 由一个一维数组及两个分别指示队列首和队列尾的变量组成(数组、队列首指针和队列尾指针)
- 类C语言定义顺序队列如下:
const int maxsize=20;
typeof struct seqqueue
{
DataType data[maxsize];
int font,rear;
}SeqQue;
SeqQue SQ;
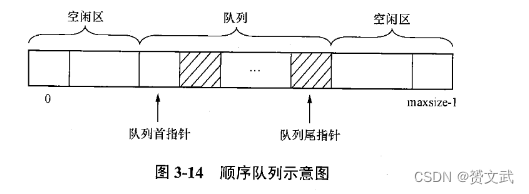
注:入队列操作
SQ.rear=SQ.rear+1;
SQ.data[SQ.rear]=x;
出队列操作:
SQ.front=SQ.front+1;
- 循环队列:将存储队列的一维数组首尾相接,形成环状
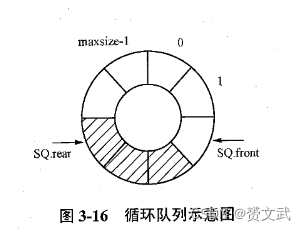
注:入队列操作如下:
SQ.rear=(SQ.rear+1)%maxsize;
SQ.data[SQ.rear]=x;
出队列操作为:
SQ.front=(SQ.front+1)%maxsize;
判队列满条件为:
((SQ.rear+1)%maxsize==SQ.front)
判断队列空的条件为:
(SQ.rear==SQ.front)
- 队列的初始化
void InitQueue(CyQue CQ)
{
CQ.front=0;
CQ.front=0;
}
- 判断队列空
int EmptyQueue(CycQue CQ)
{
if(CQ.rear==CQ.front)return 1;
elsereturn 0;
}
- 入队列
int EnQueue(CycQue CQ,DataType x)
{
if ((CQ.rear+1)%maxsize==CQ.front){error("队列满");return 0;} //队列满,入队列失败
else{CQ.rear=(CQ.rear+1)%maxsize;CQ.data[CQ.rear]=x;return 1;{
}
- 出队列
int OutQueue(CycQue CQ)
{
if(EmptyqUEUE(CQ)){error("队列空");return 0;}
else{CQ.front=(CQ.front+1)%maxsize; //不为空,出队列return 0;
}
}
- 取 队列首元素
DataType GetHead(CycQue CQ)
{
if (EmptyQueue(CQ))return NULLData;
elsereturn CQ.data[(CQ.front+1)%maxsize];
}
队列的链接实现
- 队列的链接实现是使用一个带头结点的单链表来表示队列
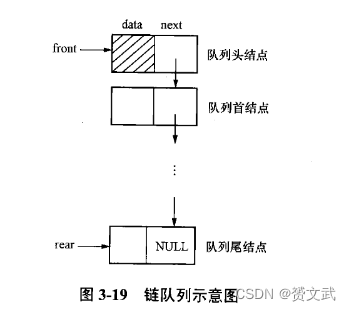
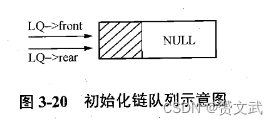
- 队列初始化
void InitQueue(LkQue *LQ)
{
LkQueNode *temp;
temp=(LkQueNode *)malloc(sizeof(LkQueNode)); //生成队列的头结点
LQ->front=temp; //队列头指针指向队列头结点
LQ->rear=temp; //尾结点指向列尾结点
(LQ->front)->next=NULL;
}
- 判断队列空
int EmptyQueue(LkQue LQ)
{
if(LQ.rear==LQ.front)return 1; //队列为空
elsereturn 0;
}
- 入队列
void EnQueue(LkQue *LQ,DataType x)
{
LkQueNode *temp;
temp=(LkQueNode *)malloc(sizeof(LkQueNode));
temp->data=x;
temp->next=NULL;
(LQ->rear)->next=temp; //新结点入队列
LQ->rear=temp; //置新的队列尾结点
}
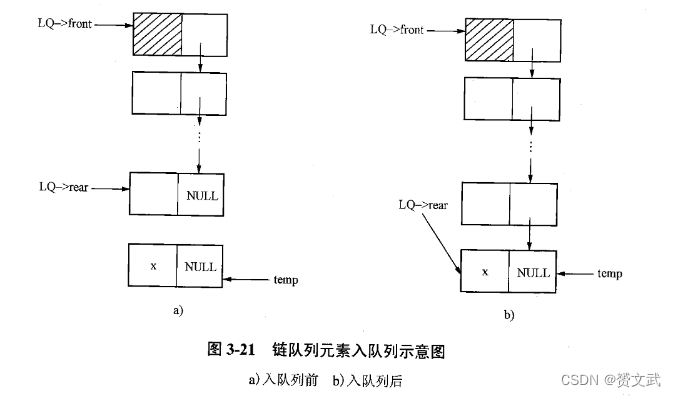
- 出队列
OutQueue(LkQue *LQ)
{
LkQueNode *temp;
if(EmptyQueuq(CQ)){error("队空");retturn 0;}
else{temp=(LQ->front)->next; //使temp指向队列的首结点(LQ——>front)——>next=temp->next; //修改头结点的指针域指向新的首结点if(temp->next=NULL)LQ->rear=LQ->front;free(temp);return 1;} }
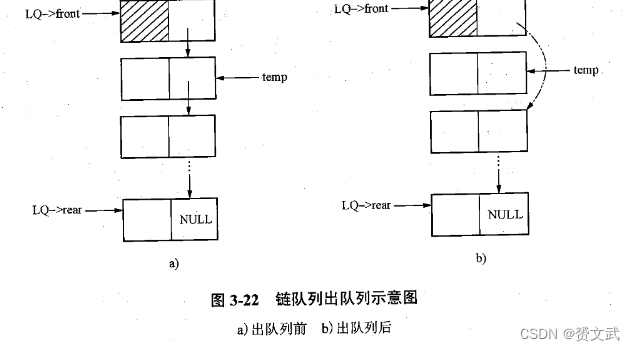
- 取队列首元素
DataType GetHead(LkQue LQ)
{
LkQueNode *temp;
if(EmptyQueue(CQ))return NULLData;
else{temp=LQ.front->next;return temp->data; //队列非空,返回队列首结点元素
}
}
数组
数组的逻辑结构和基本运算
- 一维数组又称为向量,由一组具有相同类型的数据元素组成,并存储在一组连续的存储单元中。一维数组中的数据元素又是一堆数组结构,则称为二维数组

数组的存储结构
- 一维数组元素的内存单位地址是连续的;二维数组有两种存储方法:以列序为主序的存储、以行序为主序的存储;类C语言编译程序中,采用以行序存储、某些语言编译程序,以列序为主序的存储方式
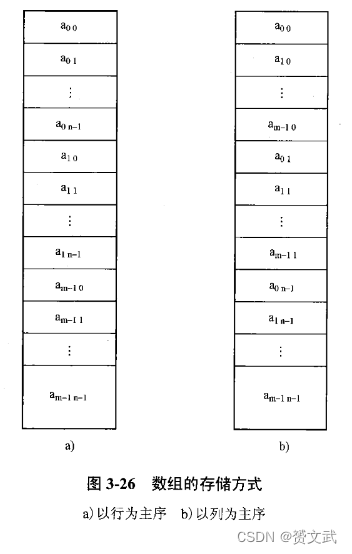
- 对于二维数组a[m][n],如果每个元素站K个存储元素,以行为主序为例;a[i][j]之前有i行元素,每行n个元素;在第i行有j+1个元素;共计ni+j+1;第一个元素距离a[i][j]相差ni+j个位置
//a[行][列]
a[3][4]

矩阵的压缩存储
- 对称矩阵:若一个n阶方阵A中满足下述条件:
aij=aji 0<=i,j<=n-1


注:设矩阵aij在数组M中位置为k,(i,j)和k存在如下关系:

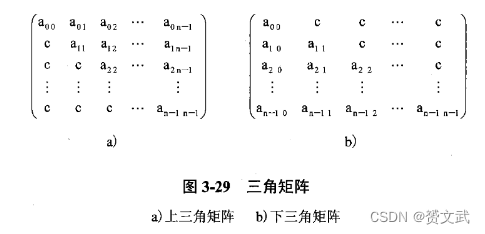
- 三角矩阵:以主对角线为界的上下半部分是一个固定的值c或零,这样的矩阵叫做上(下)三角矩阵

- 稀疏矩阵:假设m行n列的矩阵有t个非零元素,当t<<m*n,则称矩阵为稀疏矩阵
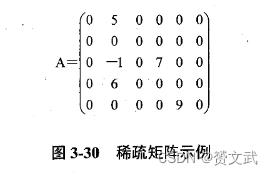
- 稀疏矩阵中所有非零元素用三元组的形式表示,并按照一定的次序组织在一起,就形成了三元组表示法
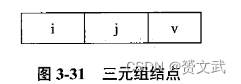
注:v为非零元素,i为非零元素v所在矩阵的行号,j为所在矩阵的列号
小试牛刀
- 栈称为________线性表;队列称为_______线性表
- 设有二维数组int M[10][20],每个元素占2个存储单位,数组的起始地址为2000,元素M[5][10]的存储位置为______,M[8][19]的存储位置为_______
- 对稀疏矩阵进行压缩存储的目的是节省_______
- 一个10X10阶对称数列A,采用行优先顺序压缩存储上三角元素,a00为第一个元素,其存储地址为0,每个元素占用1个存储单元,则a45的地址为______
- 对吸收矩阵进行压缩存储的目的是节省______
- 一个队列的输入序列是1,2,3,4,则队列的输出序列是_______
- 元素进栈次序为A,B,C,D,E,则栈中的出栈顺序可能为_________
相关文章:

第三章 栈、队列和数组
第三章 栈、队列、数组 栈栈的基本概念栈的顺序实现栈的链接实现栈的简单应用和递归 队列队列的基本概念队列的顺序实现队列的链接实现 数组数组的逻辑结构和基本运算数组的存储结构矩阵的压缩存储 小试牛刀 栈和队列可以看作是特殊的线性表,是运算受限的线性表 栈 …...
使用GitLab CI/CD 定时运行Playwright自动化测试用例
创建项目并上传到GitLab npm init playwright@latest test-playwright # 一路enter cd test-playwright # 运行测试用例 npx playwright test常用指令 # Runs the end-to-end tests. npx playwright test# Starts the interactive UI mode. npx playwright...

Suricata + Wireshark离线流量日志分析
目录 一、访问一个404网址,触发监控规则 1、使用python搭建一个虚拟访问网址 2、打开Wireshark,抓取流量监控 3、在Suricata分析数据包 流量分析经典题型 入门题型 题目:Cephalopod(图片提取) 进阶题型 题目:抓到一只苍蝇(数据包筛选…...

JMeter基础 —— 使用Badboy录制JMeter脚本!
1、使用Badboy录制JMeter脚本 打开Badboy工具开始进行脚本录制: (1)当我们打开Badboy工具时,默认就进入录制状态。 如下图: 当然我们也可以点击录制按钮进行切换。 (2)在地址栏中输入被测地…...
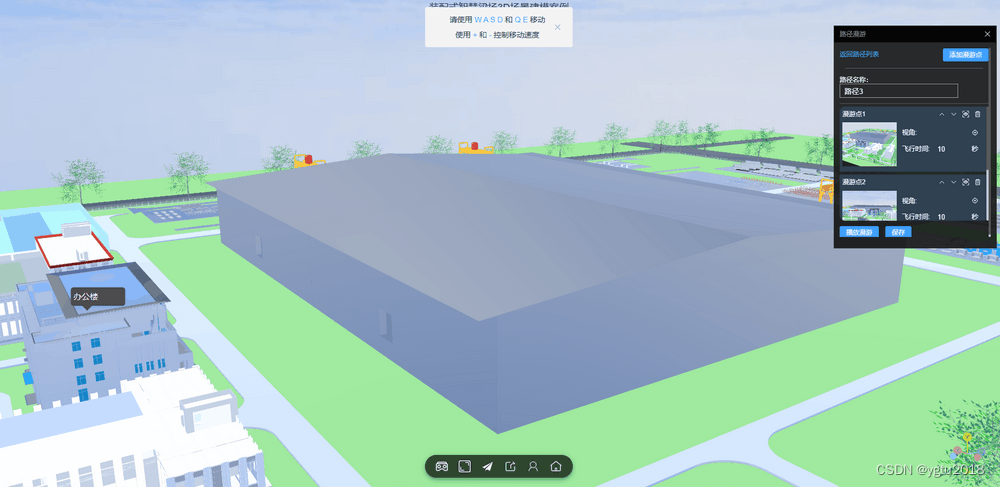
3D孪生场景搭建:3D漫游
上一篇 文章介绍了如何使用 NSDT 编辑器 制作模拟仿真应用场景,今天这篇文章将介绍如何使用NSDT 编辑器 设置3D漫游。 1、什么是3D漫游 3D漫游是指基于3D技术,将用户带入一个虚拟的三维环境中,通过交互式的手段,让用户可以自由地…...

三、综合——计算机应用基础
文章目录 一、计算机概述二、计算机系统的组成三、计算机中数据的表示四、数据库系统五、多媒体技术5.1 多媒体的基本概念5.2 多媒体计算机系统组成5.3 多媒体关键硬件一、计算机概述 1854 年,英国数学家布尔(George Boo1e,1824-1898 年)提出了符号逻辑的思想,数十年后形成了…...
【Redis】SpringBoot整合redis
文章目录 一、SpringBoot整合二、RedisAutoConfiguration自动配置类1、整合测试一下 三、自定义RedisTemplete1、在测试test中使用自定义的RedisTemplete2、自定义RedisTemplete后测试 四、在企业开发中,大部分情况下都不会使用原生方式编写redis1、编写RedisUtils代…...
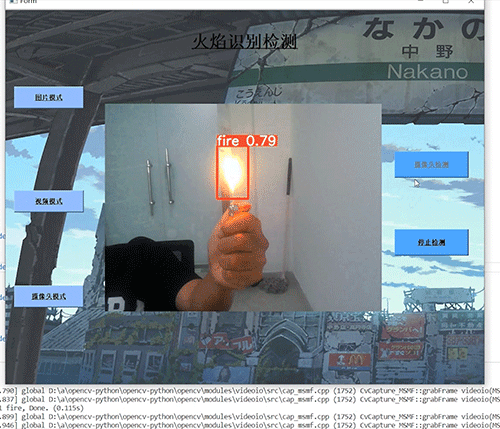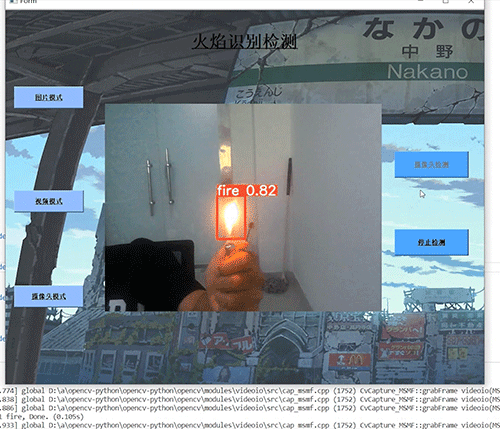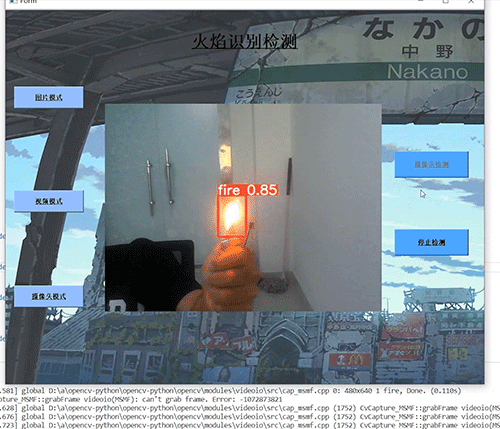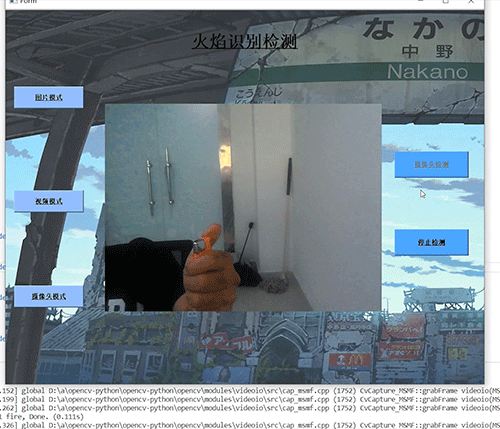
竞赛选题 深度学习 python opencv 火焰检测识别 火灾检测
文章目录 0 前言1 基于YOLO的火焰检测与识别2 课题背景3 卷积神经网络3.1 卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 YOLOV54.1 网络架构图4.2 输入端4.3 基准网络4.4 Neck网络4.5 Head输出层 5 数据集准备5.1 数…...

Python Parser 因子计算性能简单测试
一直以来,Python 都在量化金融领域扮演着至关重要的角色。得益于 Python 强大的库和工具,用户在处理金融数据、进行数学建模和机器学习时变得更加便捷。但作为一种解释性语言,相对较慢的执行速度也限制了 Python 在一些需要即时响应的场景中的…...
【java学习】特殊流程控制语句(8)
文章目录 1. break语句2. continue语句3. return语句4. 特殊流程语句控制说明 1. break语句 break语句用于终止某个语句块的执行,终止当前所在循环。 语法结构: { ...... break; ...... } 例子如下: (1&…...

pyinstaller 使用
python 打包不依赖于系统环境的应用总结 【pyd库和pyinstaller可执行程序的区别: 在实际开发中,对于多人协作的大型项目, 或者是基于支持Python的商业软件的二次开发等, 如果将py脚本打包成exe可执行文件,不仅不方便调用ÿ…...

ELK集群 日志中心集群
ES:用来日志存储 Logstash:用来日志的搜集,进行日志格式转换并且传送给别人(转发) Kibana:主要用于日志的展示和分析 kafka Filebeat:搜集文件数据 es-1 本地解析 vi /etc/hosts scp /etc/hosts es-2:/etc/hosts scp /etc…...

有哪些适合初级程序员看的书籍?
1、《C Primer Plus》(中文版名《C Primer Plus(第五版)》) 作者:Stephen Prata 该书以C语言为例,详细介绍了编程语言的基础知识、控制结构、函数、指针、数组、字符串、结构体等重要概念。并且࿰…...
)
uniapp iosApp H5+本地文件操作(写入修改删除等)
h5 地址 html5plus 以csv文件为例,写入读取保存修改删除文件内容,传输文件等 1.save 文件保存 function saveCsv(data,pathP,path){// #ifdef APP-PLUSreturn new Promise((resolve, reject) > {plus.io.requestFileSystem( plus.io.PUBLIC_DOCUMEN…...

蓝桥杯 字符串和日期
有一个类型的题目是找到输出图形的规律,然后将其实现。观察下面的图形。你想想你该怎么输出这个图形呢? ABBB#include<stdio.h> int main(){printf(" A\n");printf("BBB\n");return 0; }那么,对于如下的图形: ABB…...

Vue13 监视属性
监视属性 当被监视的属性发生变化时,执行定义的函数 监视属性watch: 1.当被监视的属性变化时, 回调函数自动调用, 进行相关操作 2.监视的属性必须存在,才能进行监视!! 3.监视的两种写法: (1).new Vue时传入…...
会员商城小程序的作用是什么
随着消费升级、用户消费习惯改变及互联网电商高速发展冲击下,传统线下经营商家面临不少痛点,产品销售难、经营营销难、客户管理难等,线下流量匮乏、受地域限制且各方面管理繁琐,线上成为众商家增长赋能的方式。 对商家来说&#x…...
排序算法——希尔排序
一、介绍: 希尔排序是一种可以减少插入排序中数据比较次数的排序算法,加速算法的进行,排序的原则是将数据区分为特定步长的小区块,然后以插入排序算法对小区块内部进行排序,经历过一轮排序则减少步长,直到所有数据都排…...

SpringBoot项目整合MybatisPlus持久层框架+Druid数据库连接池
前言 之前搭建SpringBoot项目工程,所使用的持久层框架不是Mybatis就是JPA,还没试过整合MybatisPlus框架并使用,原来也如此简单。在此简单记录一下在SpringBoot项目中,整合MybatisPlus持久层框架、Druid数据库连接池的过程。 一、…...
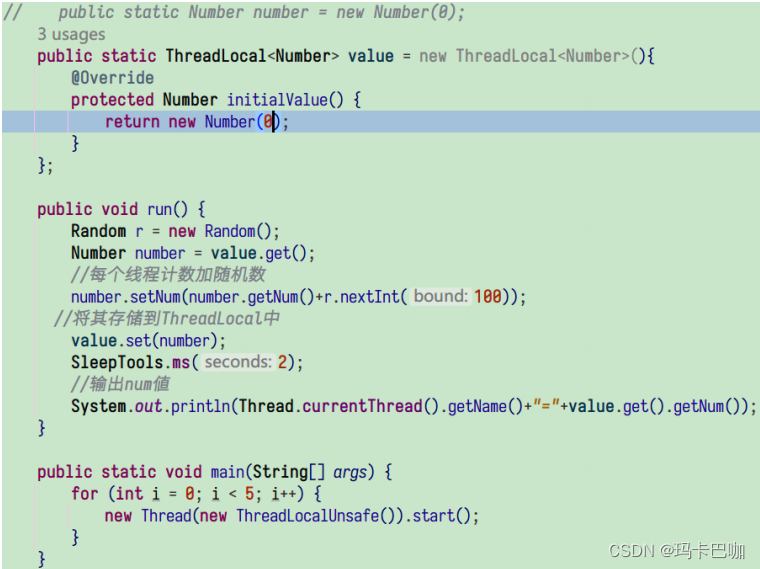
导致 JVM 内存泄露的 ThreadLocal 详解
为什么要有 ThreadLocal 当我们在学习JDBC时获取数据库连接时,每次CRUD的时候都需要再一次的获取连接对象,并把我们的sql交给连接对象实现操作。 在实际的工作中,我们不会每次执行 SQL 语句时临时去建立连接,而是会借助数据库连接…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
