关于GD32引脚PA13、PA15、PB3、PB4配置为普通引脚的问题
关于GD32引脚PA13、PA15、PB3、PB4配置为普通引脚的问题
在实际开发中,经常会遇到引脚资源受限需要将一些具有特定功能的引脚配置为普通引脚或其他引脚功能使用的情况。
博主之前遇到过类似的情况,都正常解决了。但偶尔也会出现在配置引脚时少了一些配置,结果导致代码运行时偶尔出现问题,最终排查出了是引脚配置问题,因此特地记录下来,供有需求的同学参考。
以GD32F307为例,在使用外置sram芯片时,使用了PB3、PB4作为SPI通讯的SCK和MISO引脚。
在代码编写和调试时,忽视了PB3和PB4的默认功能是JTDO和NJTRST功能,直接将PB3、PB4当做普通SPI引脚使用,由于我调试时一致使用JLINK连接芯片进行在线调试,在这个时候sram芯片的驱动一直正常,读写数据也正常,也导致我再一开始没有发现这个问题。
后来交给测试人员测试功能时,反馈有时候出现数据丢失的情况。博主排查后发现是sram读写数据失败导致,用示波器排查波形发现在在读写sram时,SCK没有时钟信号发出。博主很奇怪,为何之前调试时没有出现过这种情况?于是乎,连接上JILNK在线调试,用示波器一看,果然,此时sram读写数据都是SCK线上是有正常时钟发出的。。。
在这种情况下,排查了数据手册(datasheet)上SPI相关的引脚,结果发现了问题的根本所在:PB3引脚默认功能为JTDO,PB4引脚默认功能是NJTRST,他们是JTAG调试方式时用的,博主使用的是SWD的方式,且这两个引脚要配置为SPI功能需要做重定向处理,即将关闭这两个引脚JTAG相关功能,这样配置之后,测试发现一切正常了。

#define GPIO_SWJ_NONJTRST_REMAP ((uint32_t)0x00300000U | (PCF0_SWJ_CFG(1) >> 16)) /*!< full SWJ(JTAG-DP + SW-DP),but without NJTRST */
#define GPIO_SWJ_SWDPENABLE_REMAP ((uint32_t)0x00300000U | (PCF0_SWJ_CFG(2) >> 16)) /*!< JTAG-DP disabled and SW-DP enabled */
#define GPIO_SWJ_DISABLE_REMAP ((uint32_t)0x00300000U | (PCF0_SWJ_CFG(4) >> 16)) /*!< JTAG-DP disabled and SW-DP disabled */
#define GPIO_SPI2_REMAP ((uint32_t)0x00200000U | (AFIO_PCF0_SPI2_REMAP >> 16)) /*!< SPI2 remapping*/
代码如下:
/*** @brief sram spi配置* @param None* @retval None*/
void sram_spi_init(void)
{spi_parameter_struct spi_init_struct;rcu_periph_clock_enable(RCU_GPIOB);rcu_periph_clock_enable(RCU_GPIOE);rcu_periph_clock_enable(RCU_SPI2);/* SPI2_SCK: PB3* SPI2_MISO:PB4* SPI2_MOSI:PB5* SPI2_CS: PE1* HOLD: PE0*/gpio_pin_remap_config(GPIO_SWJ_SWDPENABLE_REMAP, ENABLE);/*PB3、PB4默认为JTAG引脚,使用SPI需失能JTAG功能,否则会导致SPI引脚功能异常,如:不DEBUG时SCK不产生时钟*/gpio_init(GPIOB, GPIO_MODE_AF_PP, GPIO_OSPEED_50MHZ, GPIO_PIN_3 | GPIO_PIN_5);//MISO引脚可配置为推挽输出、浮空输入、上拉输入皆可gpio_init(GPIOB, GPIO_MODE_IN_FLOATING, GPIO_OSPEED_50MHZ, GPIO_PIN_4);gpio_init(GPIOE, GPIO_MODE_OUT_PP, GPIO_OSPEED_50MHZ, GPIO_PIN_1);//此处硬件改线占用了板子DI引脚,后续硬件版本会有改动gpio_init(GPIOE, GPIO_MODE_OUT_PP, GPIO_OSPEED_50MHZ, GPIO_PIN_0);/*HOLD引脚设置为1禁用该功能*/spi_init_struct.trans_mode = SPI_TRANSMODE_FULLDUPLEX;spi_init_struct.device_mode = SPI_MASTER;spi_init_struct.frame_size = SPI_FRAMESIZE_8BIT;spi_init_struct.clock_polarity_phase = SPI_CK_PL_LOW_PH_1EDGE;//重要!重要!重要!该SRAM芯片需要配置为时钟空闲时为低电平,在第一个跳变沿采样spi_init_struct.nss = SPI_NSS_SOFT;//默认为软件NSSspi_init_struct.prescale = SPI_PSC_8;//注意SPI芯片支持的最高速率spi_init_struct.endian = SPI_ENDIAN_MSB;spi_init(SPI2, &spi_init_struct);SPI_SRAM_CS_HIGH();//初始拉高CSSPI_SRAM_HOLD_HIGH();//HOLD默认为高,禁用该功能,否则可能导致读写失败spi_enable(SPI2);
}
因此,在使用到引脚PA13、PA15、PB3、PB4等比较特殊的引脚时,一定仔细查看下手册上的定义再进行配置。
相关文章:

关于GD32引脚PA13、PA15、PB3、PB4配置为普通引脚的问题
关于GD32引脚PA13、PA15、PB3、PB4配置为普通引脚的问题 在实际开发中,经常会遇到引脚资源受限需要将一些具有特定功能的引脚配置为普通引脚或其他引脚功能使用的情况。 博主之前遇到过类似的情况,都正常解决了。但偶尔也会出现在配置引脚时少了一些配…...

JS-Dom转为图片,并放入pdf中进行下载
1、将dom转换为图片 这里我们使用html2canvas工具插件先将dom转为canvas元素然后canvas拥有一个方法可以将绘制出来的图形转为url然后下载即可注意:如果元素使用了渐变背景并透明的话,生成的图片可能会有点问题。我下面这个案例使用了渐变背景实现元素对…...
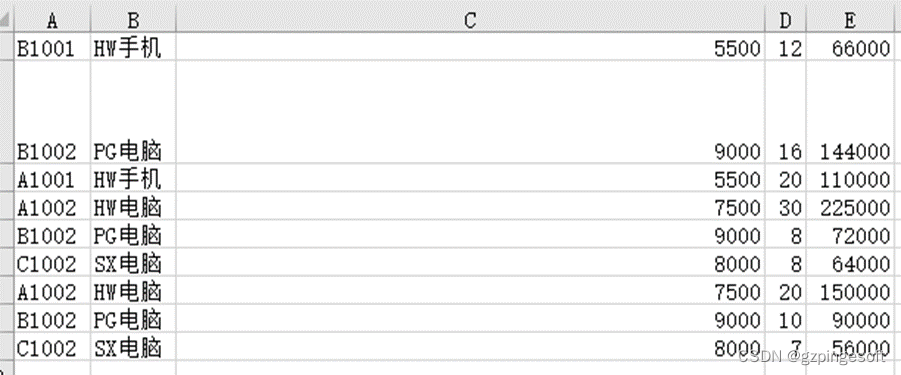
Python 无废话-办公自动化Excel格式美化
设置字体 在使用openpyxl 处理excel 设置格式,需要导入Font类,设置Font初始化参数,常见参数如下: 关键字参数 数据类型 描述 name 字符串 字体名称,如Calibri或Times New Roman size 整型 大小点数 bold …...

Python视频剪辑-Moviepy音频效果afx方法
随着多媒体内容在日常生活和工作中的广泛应用,音频处理成为了一个越来越重要的技能。无论是在游戏开发、音乐制作,还是在各种应用和网站中,高质量的音频处理都能极大地提升用户体验。然而音频处理看似复杂,实则不必如此。其实只需要掌握一些基础的概念和技巧,就能够完成大…...

让LLM模型输入token无限长
背景 增加LLM的输入token已经有很多的研究,但是思路无外乎:模型抽取局部特征通过上层通过模型融合预测最终解,以及这个思路的一些变种。然而这些思路其实都没能很彻底的解决无限长token问题,根据《EFFICIENT STREAMING LANGUAGE …...
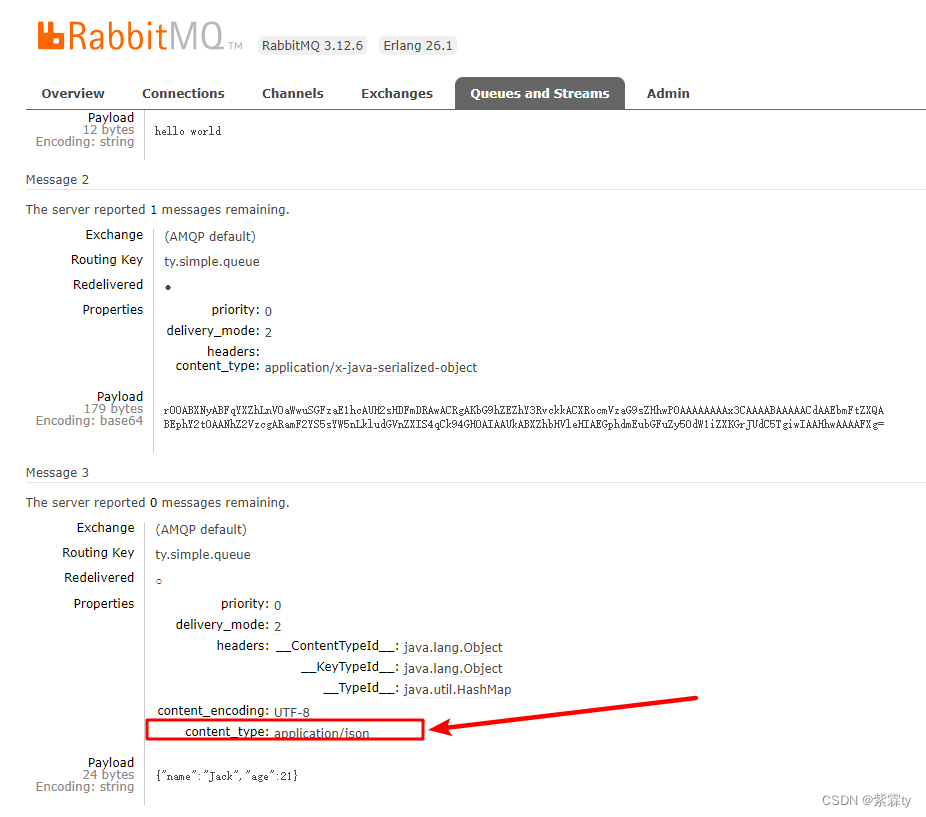
RabbitMQ 介绍与 SpringBootAMQP使用
一、MQ概述 异步通信的优点: 耦合度低吞吐量提升故障隔离流量削峰 异步通信的缺点: 依赖于Broker的可靠性、安全性、吞吐能力架构复杂,业务么有明显的流程线,不方便追踪管理 什么是的MQ MQ(Message Queue…...

企业门户的必备选择,WorkPlus的定制化解决方案
在当今数字化时代,企业门户成为了企业内外沟通与协作的重要基础设施。WorkPlus作为领先的品牌,为企业提供了一站式的企业门户解决方案,旨在提升企业形象、改善内外部沟通与协作效率。本文将深入探讨WorkPlus如何通过定制化的设计,…...

基于maven的项目搭建(已跑通)
1、直接选择archetype-webapp即可 (这里很多人会觉得很慢–解决方案:https://blog.csdn.net/qq_45591895/article/details/133705674?spm1001.2014.3001.5501) 2、手动添加一个java目录即可。 3、添加Tomcat 3、这就跑通了,可以…...

L1-035 情人节 c++解法
题目再现 以上是朋友圈中一奇葩贴:“2月14情人节了,我决定造福大家。第2个赞和第14个赞的,我介绍你俩认识…………咱三吃饭…你俩请…”。现给出此贴下点赞的朋友名单,请你找出那两位要请客的倒霉蛋。 输入格式: 输入…...

DecimalFormat 多语言、本地化指定Locale
DecimalFormat再未指定Locale会使用默认的Locale,不同的Locale会导致格式化时出现出乎预期的现象。如Locale为西班牙时,小数点符号为",“千位分隔符为”."。 所以在多语言或者需要本地化的情况下,使用DecimalFormat最好指定Locale避…...

冲刺第十五届蓝桥杯P0003倍数问题
文章目录 原题连接解析代码 原题连接 倍数问题 解析 需要找出三个数字,三个数字之和是k的倍数,并且这个数字需要最大,很容易想到的就是将数组进行倒叙排序,然后三层for循环解决问题,但是这样会导致**时间复杂度很高…...

操作系统备考学习 day7 (2.3.4 ~ 2.3.5)
操作系统备考学习 day7 第二章 进程与线程2.3 同步与互斥2.3.4 信号量 用信号量实现进程互斥、同步、前驱关系信号量机制实现进程互斥信号量机制实现进程同步信号量机制实现前驱关系 2.3.5 经典同步问题生产者-消费者问题多生产者和多消费者模型抽烟者问题读者-写者问题哲学家进…...
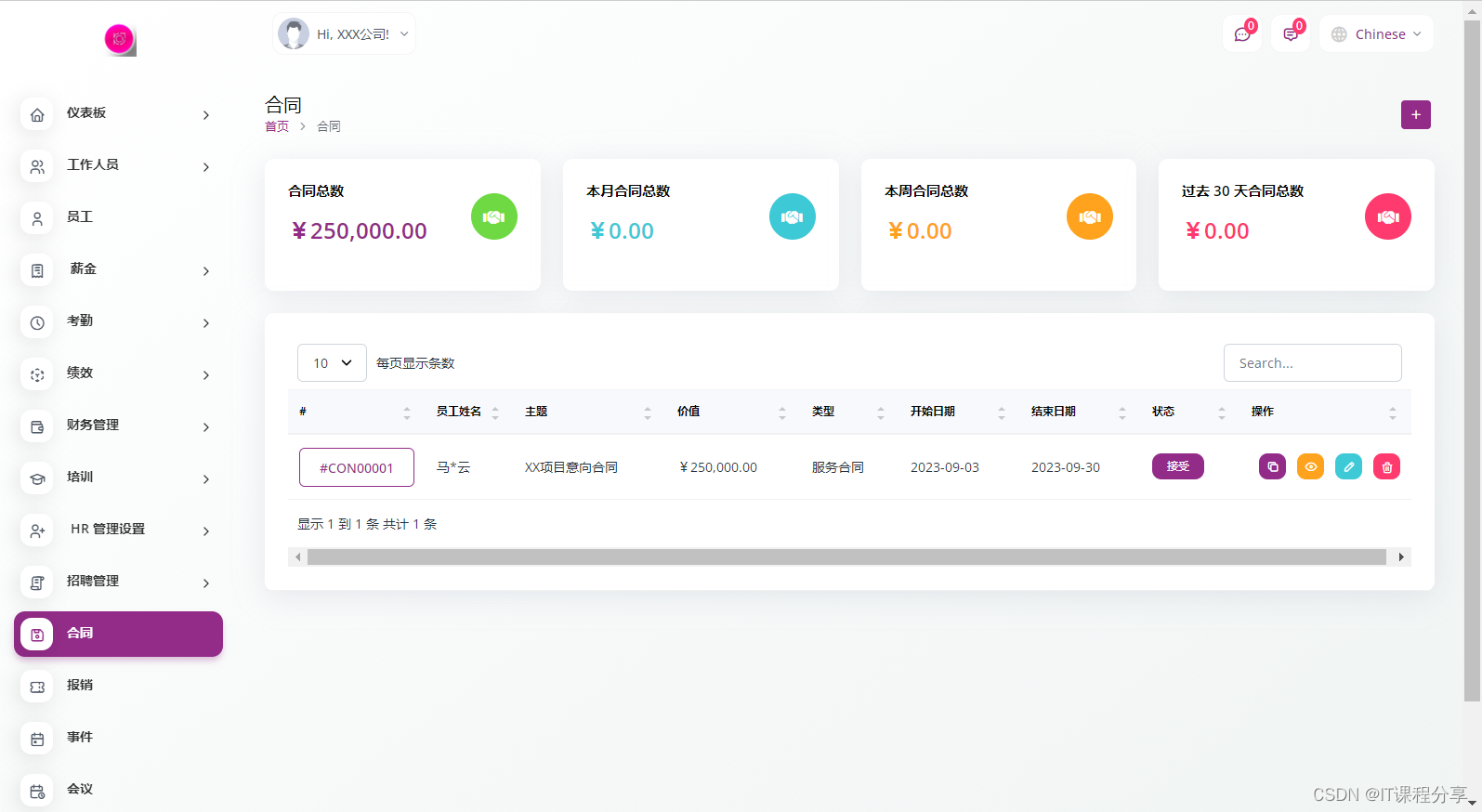
HRM人力资源管理系统源码
HRM人力资源管理系统源码 运行环境:PHP8.1或以上 MYSQL5.7或以上 php扩展要求 fileinfo imagemagick 功能介绍: 综合仪表板 它通过其综合仪表板提供了员工总数、工单和帐户余额的概览。 您可以轻松访问组织中的缺席者以及详细的公告和预定会议列…...
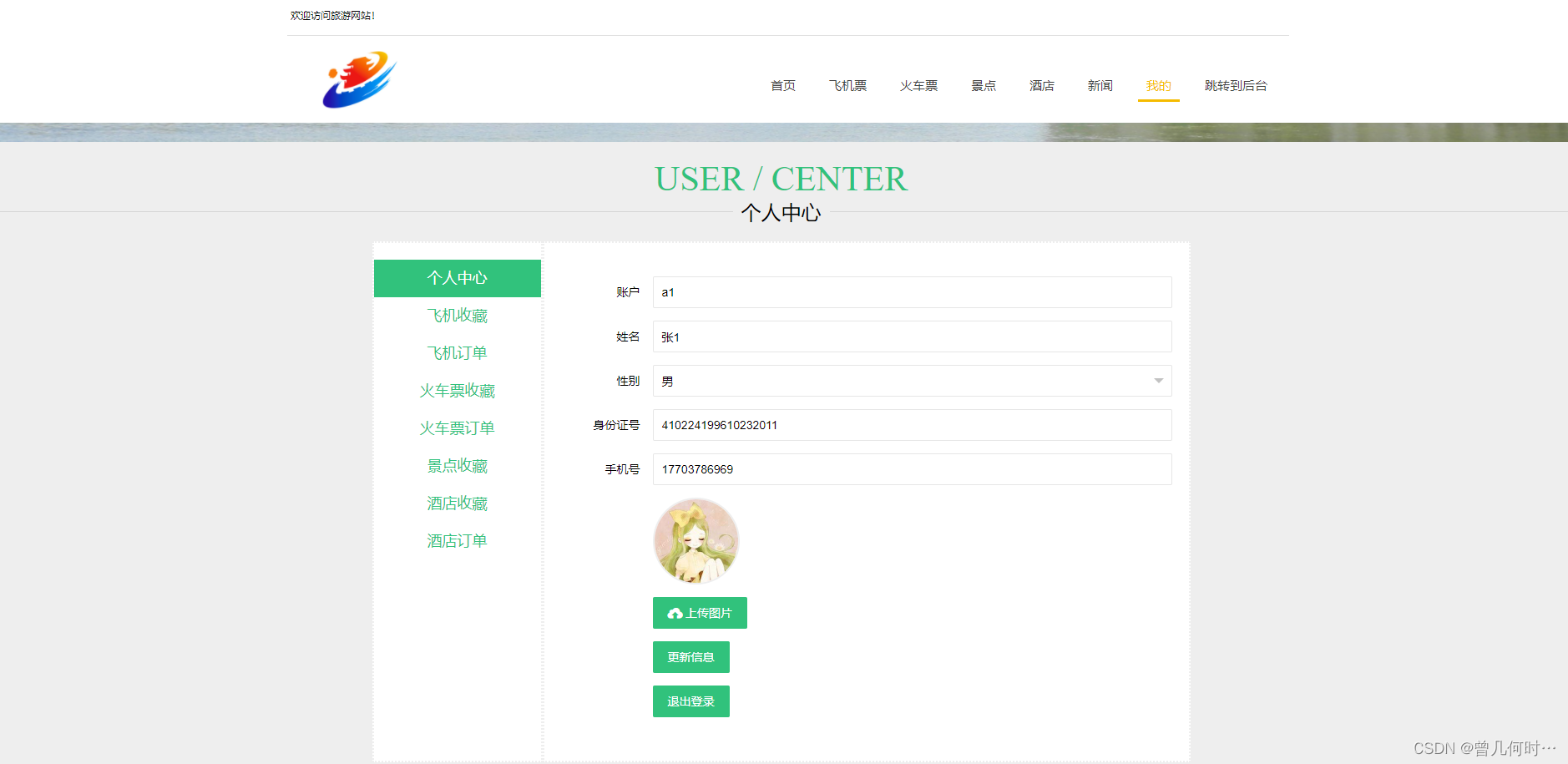
基于SSM的旅游网站设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
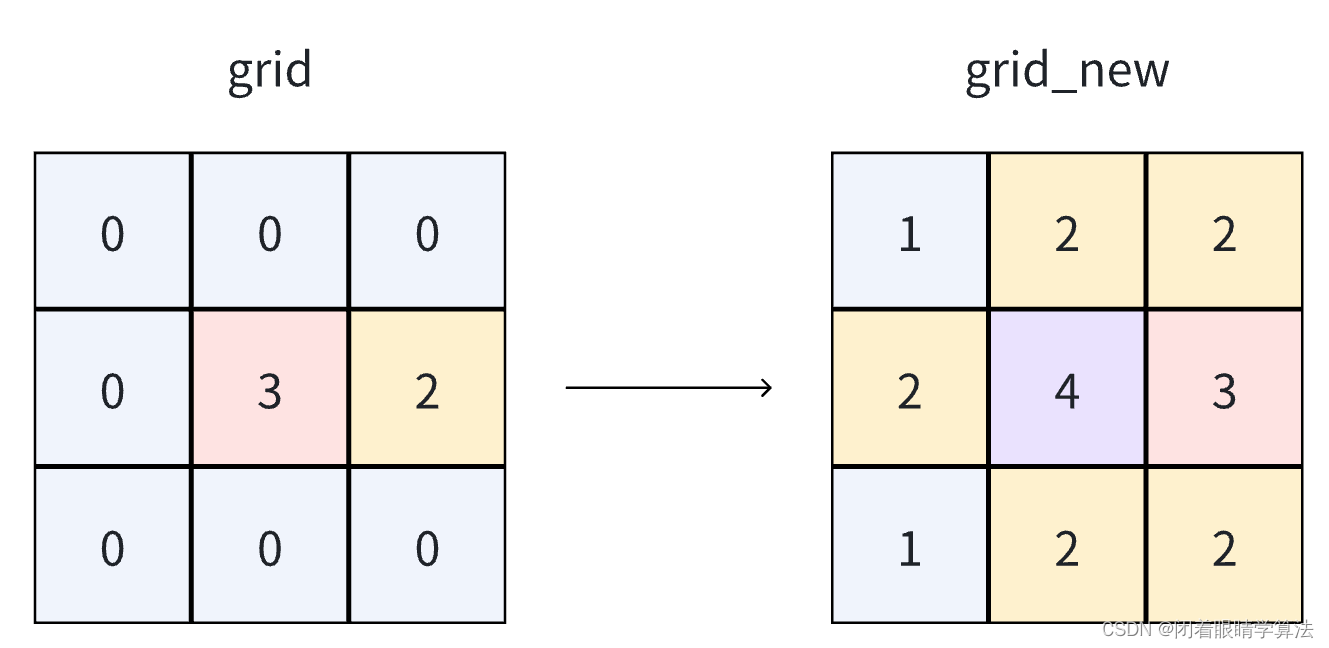
大厂秋招真题【BFS+DP】华为20230921秋招T3-PCB印刷电路板布线(留学生专场)
华为20230921秋招T3-PCB印刷电路板布线(留学生专场) 题目描述与示例 题目描述 在PCB印刷电路板设计中,器件之间的连线,要避免线路的阻抗值增大,而且器件之间还有别的器任和别的干扰源,在布线时我们希望受…...

OpenCV Python – 使用SIFT算法实现两张图片的特征匹配
OpenCV Python – 使用SIFT算法实现两张图片的特征匹配 1.要实现在大图中找到任意旋转、缩放等情况下的小图位置,可以使用特征匹配算法,如 SIFT (尺度不变特征变换) 或 SURF (加速稳健特征)。这些算法可以在不同尺度和旋转情况下寻找匹配的特征点 impo…...

doc转html后添加style和导航
public static void main(String[] args) throws Exception {docxToHtml(); } public static void docxToHtml() throws Exception {//D:\zpdtolly\工作总结文档\zpd使用文档\v4\用户使用手册\客户端使用手册String sourceFileName "C:\\Users\\luoguoqing\\Desktop\\202…...

Python中跨越多个文件使用全局变量
嗨喽,大家好呀~这里是爱看美女的茜茜呐 这个琐碎的指南是关于在 Python 中跨多个文件使用全局变量。 但是在进入主题之前,让我们简单地看看全局变量和它们在多个文件中的用途。 👇 👇 👇 更多精彩机密、教程ÿ…...
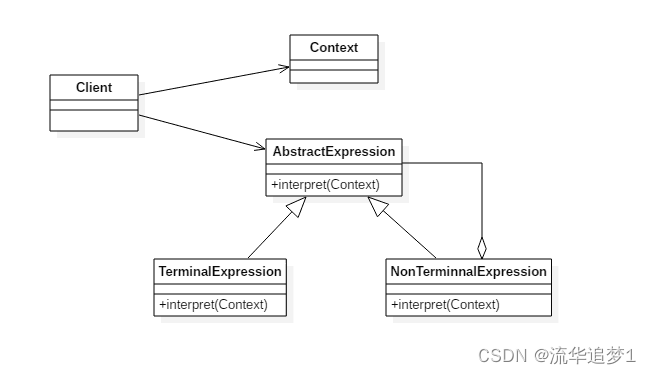
设计模式 - 解释器模式
目录 一. 前言 二. 实现 三. 优缺点 一. 前言 解释器模式(Interpreter Pattern)指给定一门语言,定义它的文法的一种表示,并定义一个解释器,该解释器使用该表示来解释语言中的句子,属于行为型设计模式。是…...

javascript禁止鼠标右键和复制功能
要禁止鼠标右键和复制功能,可以编写如下的封装函数: function preventDefaultCopy(event) {// 禁止右键 菜单和复制event.preventDefault();event.stopPropagation();return false; }// 在需要禁止复制的元素上添加该事件监听器 element.addEventListen…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
