数据结构与算法设计分析——贪心算法的应用
目录
- 一、贪心算法的定义
- 二、贪心算法的基本步骤
- 三、贪心算法的性质
- (一)最优子结构性质
- (二)贪心选择性质
- 四、贪心算法的应用
- (一)哈夫曼树——哈夫曼编码
- (二)图的应用——求最小生成树
- 1、普里姆算法(Prim)
- 2、克鲁斯卡尔算法(Kruskal)
- 3、两种算法的比较
- (三)图的应用——求单源最短路径
- 迪杰斯特拉算法(Dijkstra)
一、贪心算法的定义
贪心算法是指不考虑整体上的综合最优决策,而在局部上以最优决策来解决问题,即每次选择的都是最优的解决方案,不考虑该决策对整体的影响。这种方法在处理一些情况下,可以得到最优解的很好近似方案,例如,哈夫曼编码、求最小生成树中的普里姆算法(Prim)、克鲁斯卡尔算法(Kruskal)、求单源最短路径中的迪杰斯特拉算法(Dijkstra)等算法。
二、贪心算法的基本步骤
- 首先,对整体最优解采用贪心算法进行
分解,将其化为若干个小规模的子问题,这些子问题是相互独立的,然后通过数学归纳法证明,在每一步的选择中,可以依据贪心策略在当前子问题中选择出最优解(局部解决,不考虑整体情况,只考虑当前),最后,将所有子问题的最优解进行整体合并,得到整体的最优解,从而解决问题,简单可归纳为三个步骤。
三、贪心算法的性质
贪心算法具有以下两大性质,若针对某一问题,若具有以下重要性质,则可以通过使用贪心算法可以得到最优解。
(一)最优子结构性质
针对一个问题,将问题分为若干个子问题,从而该问题的最优解分割成若干个子问题的最优解来解决,然后通过递推从而得到该问题的最优解,即最优子结构性质。所以,具有这种性质的问题,才能保证通过贪心算法得到的解是最优解。【可分割,局部】
(二)贪心选择性质
在求解问题时,每一步都采取在当前情况下最优的选择,即每次选择都是在局部中选择最优解,从而最终得到的解是整体最优解(最近似),即贪心选择性质。【局部最优】
四、贪心算法的应用
在《数据结构》中贪心算法的常见应用场景有以下,例如,哈夫曼树中的哈夫曼编码,图的应用中求最小生成树以及求单源最短路径的相关算法。
(一)哈夫曼树——哈夫曼编码
注:求哈夫曼编码时,最小频率和最小权值等同,这里以最小权值为例介绍。
简单的来说,哈夫曼编码是可变字长编码(VLC)的一种,常用于数据的压缩,压缩率在20%~90%。哈夫曼树以及哈夫曼编码的基本概念,可以回顾一下之前的文章:数据结构学习笔记——哈夫曼树
例如,画出以3,4,6,8,12,13,15,18,25,40为结点权值所构造的哈夫曼树,并对各结点编码。
解:选取权值最小的两个结点:3和4,相加3+4=7,新的根结点为7,将其插入到树的集合中:
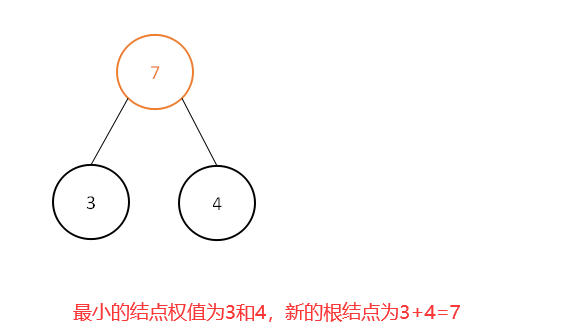
此时集合中为[6,7,8,12,13,15,18,25,40],继续选取最小的两个结点权值:
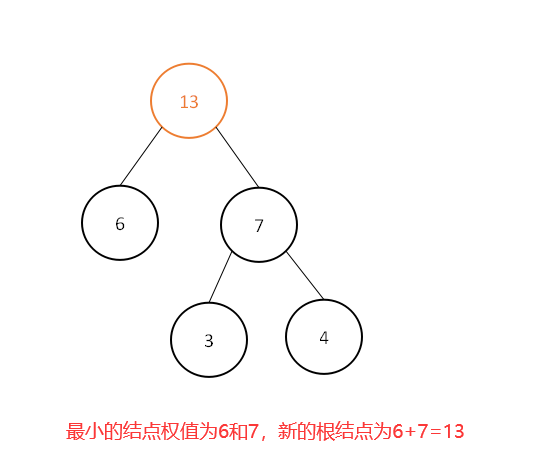
此时集合中为[8,12,13,13,15,18,25,40],继续选取最小的两个结点权值:
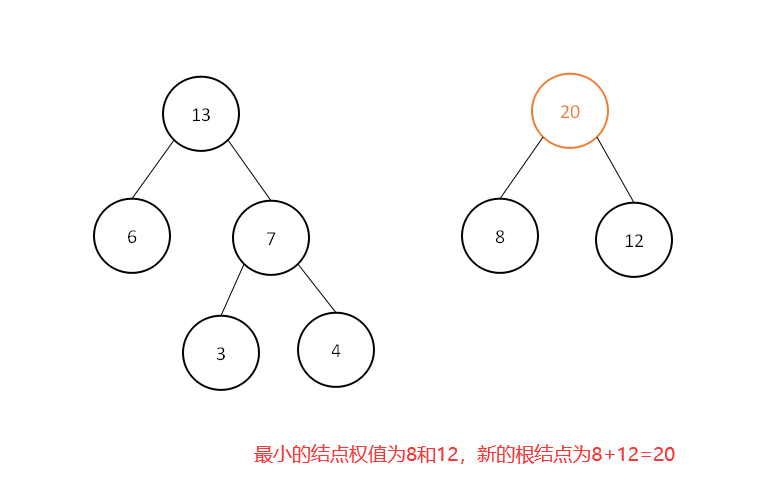
此时集合中为[13,13,15,18,20,25,40],继续选取最小的两个结点权值:
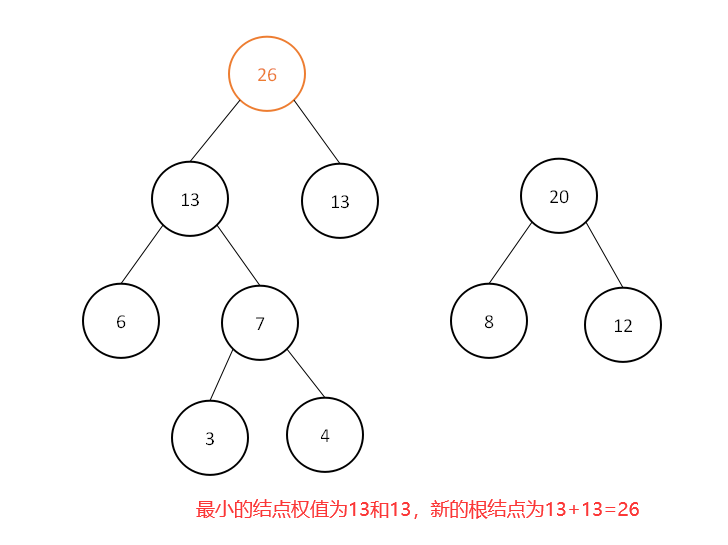
此时集合中为[15,18,20,25,26,40],继续选取最小的两个结点权值:
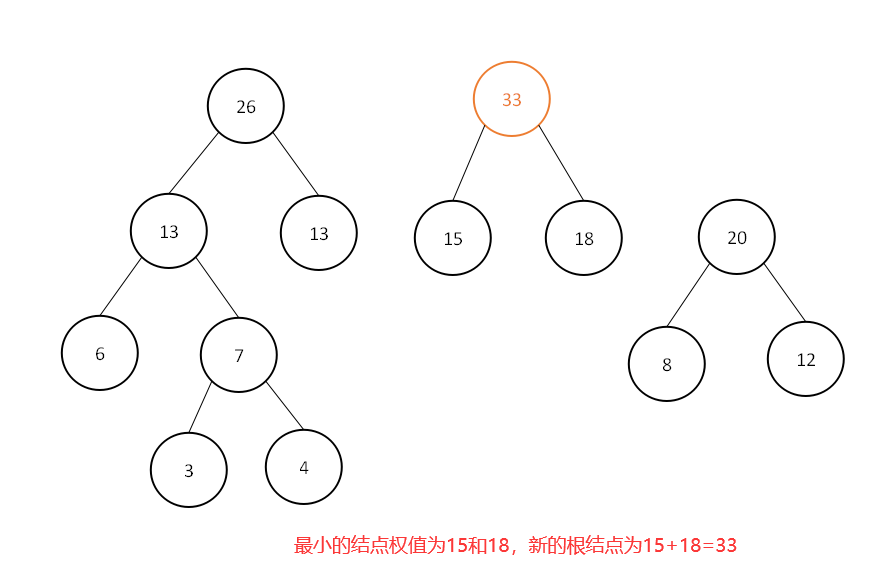
此时集合中为[20,25,26,33,40],继续选取最小的两个结点权值:

此时集合中为[26,33,40,45],继续选取最小的两个结点权值:
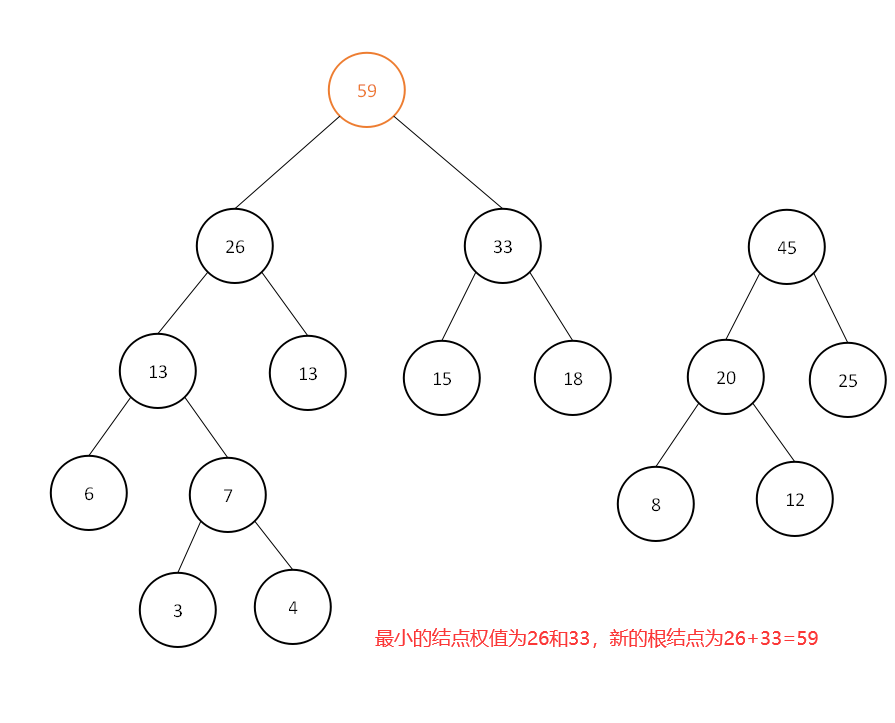
此时集合中为[40,45,59],继续选取最小的两个结点权值:
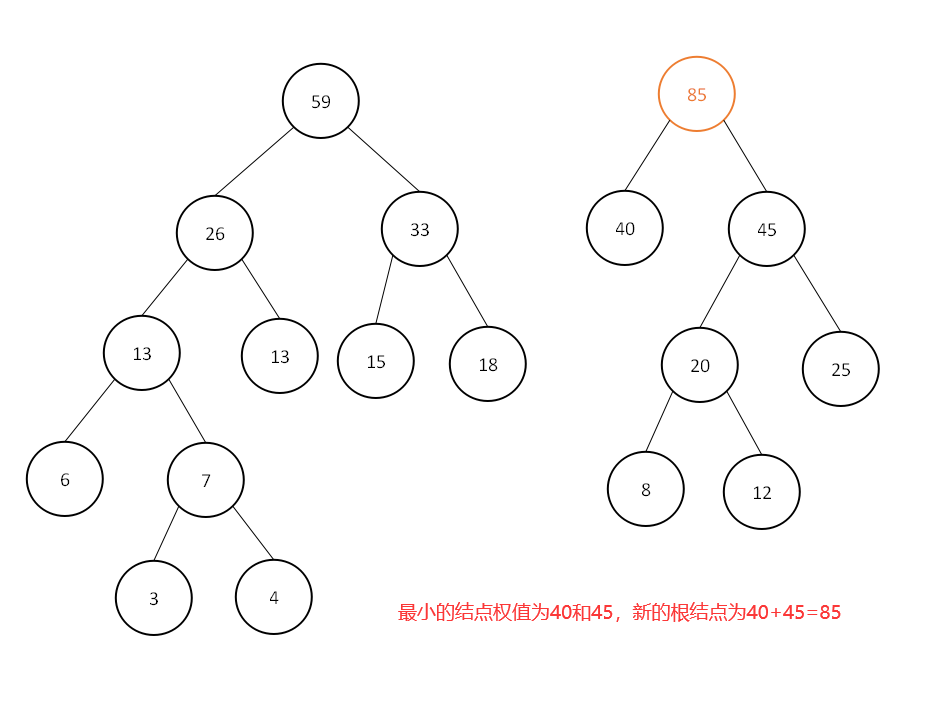
此时集合中为[59,85],继续选取最小的两个结点权值:
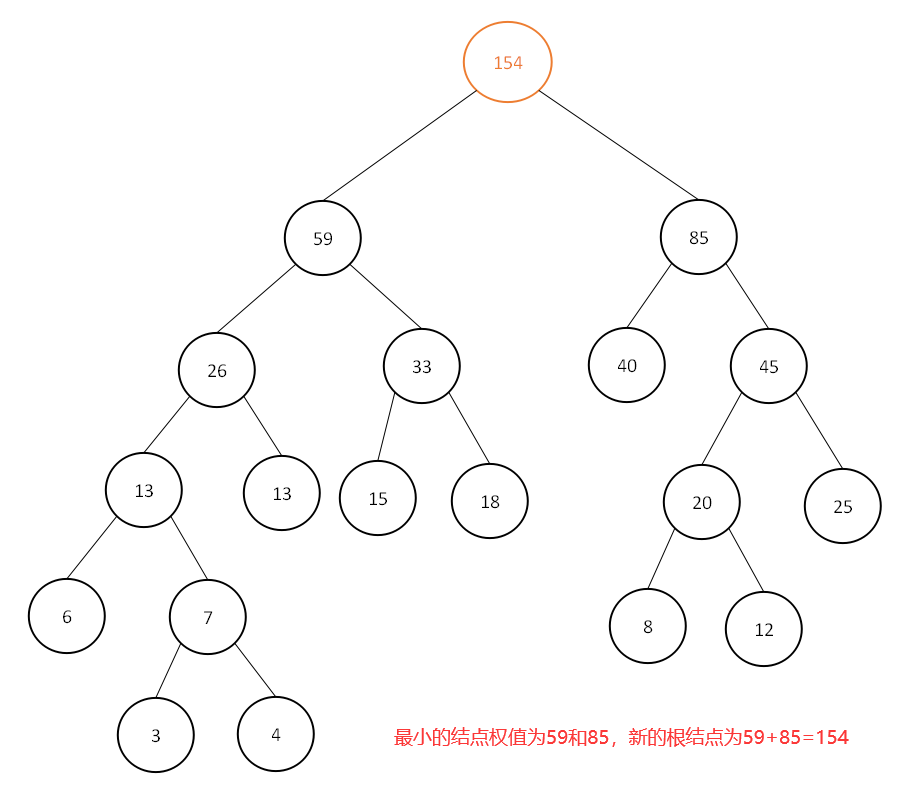
即为最终的哈夫曼树,设左分支为0,右分支为1,如下:
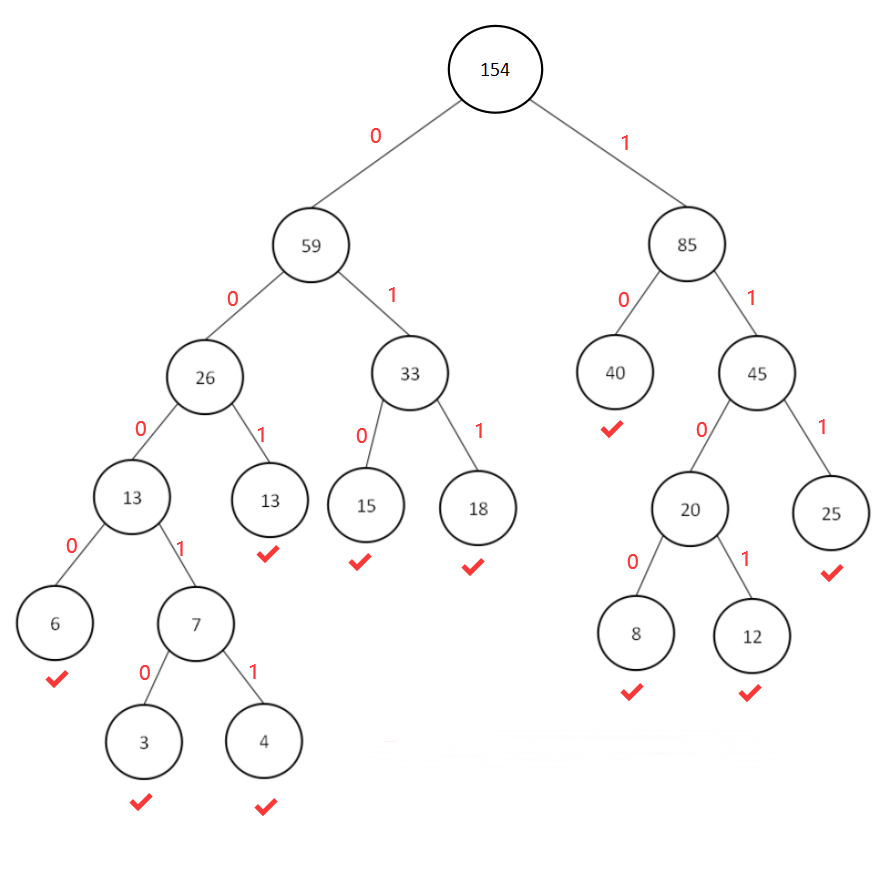
则各叶子结点的哈夫曼编码如下:
3:00010
4:00011
6:0000
8:1100
12:1101
13:001
15:010
18:011
25:111
40:10
从以上过程中,不难看出,每次的选择都是选取两棵根结点权值最小的树作为左、右子树,新的二叉树的根结点权值为其权值之和,然后将原先两个结点从森林中删除,新的结点添加进去……,按照由下至上依次构造哈夫曼树,最上层的权值最大。
1、哈夫曼编码的最优子结构性质
- 针对哈夫曼树,对字符进行编码,将要编码的字符作为叶子节点,两两组合,从下往上,通过执行n-1次的合并产生新的根结点,依次进行下去,得到最终的哈夫曼编码。
由于每次选择的都是两个最小权值结点,从而构成了一个局部最优解。【局部最优】
n个结点的哈夫曼树可形成共2n-1个结点,且叶子结点的个数也为n,分支结点的个数=总结点数-叶子结点数=2n-1-n=n-1,即有n-1次合并。
2、哈夫曼编码的贪心选择性质
- 每次选择当前两个或权值最小的结点构造一颗子树的根结点,其权值为权值之和,并把产生的子树的根结点再插入到队列中,最后,按结点的权值大小为最小优先队列。
由于每次选择的情况都是最小权值结点,所以这两个结点之和一定是最优解。【选择最优】
(二)图的应用——求最小生成树
简单的来说,含有n个顶点的最小生成树有以下特点:
①最小生成树不唯一;
②最小生成树是一个无环图(不形成回路);
③最小生成树中包含图的所有顶点;
④最小生成树在所有生成树中该树的各边权值之和最小;
⑤最小生成树生成树的边的个数为n-1;
在生成最小生成树时可以选择不同的边,所以最小生成树不唯一(存在权值相同的边),但若当图G的各边权值不同,则此时最小生成树是唯一的,所以最小生成树的边的权值之和总是唯一的。
最小生成树的概念,可以回顾一下之前的文章:数据结构学习笔记——图的应用1(最小生成树、最短路径)
1、普里姆算法(Prim)
普里姆算法的步骤如下:
①从顶点集V中任意选取一个顶点,然后将与该顶点邻接的边中选取一条权值最小的边,将其并入,从而得到一棵树;
②继续选取邻接的边中最短的边(权值最小),连接边,并入树中(若有相同权值,则任选一条即可);
③直到图中的所有顶点都被并入,得到最小生成树。
- 普里姆算法适用于求
边稠密的网的最小生成树,由于每次都是选择一个点与其他剩下点的之间的最短边(最小权值),所以其时间复杂度与图的边数无关,核心语句是在集顶点集V中寻找最近的顶点,所以n个顶点、e条边的无向连通带权图,其时间复杂度为O(n2)。
例如,下面是一个无向带权连通图,采用普里姆算法生成最小生成树:
任意选取一个顶点为起点开始,这里选取V1为例。
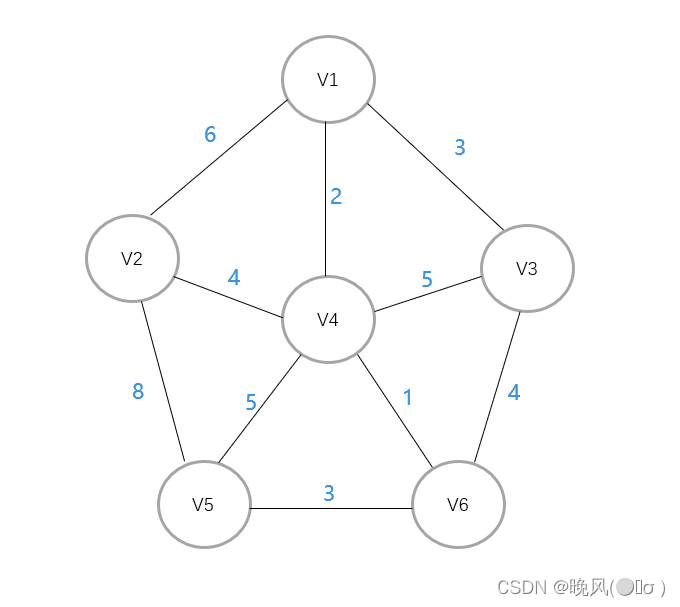
此时邻接的边的权值分别为[2、3、6],取最小权值2,所以V1与邻接的顶点V4相连:
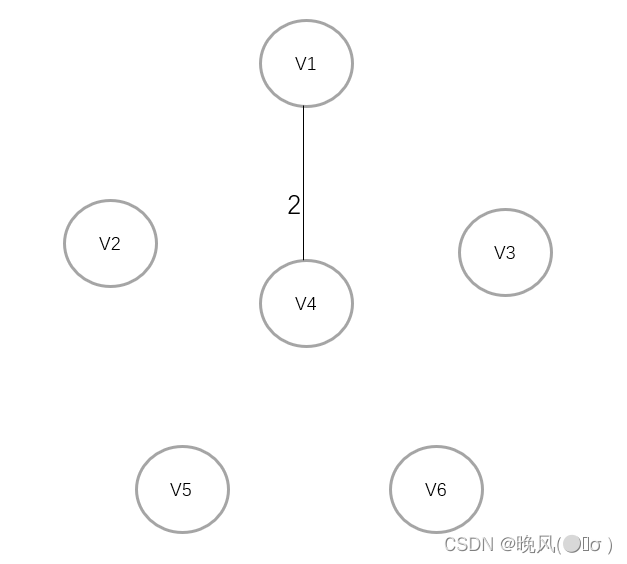
此时邻接的边的权值分别为1、4、5、5,以及加上前面的3、6,即[1、3、4、5、5、6],取最小权值1,所以V4与邻接的顶点V6相连:
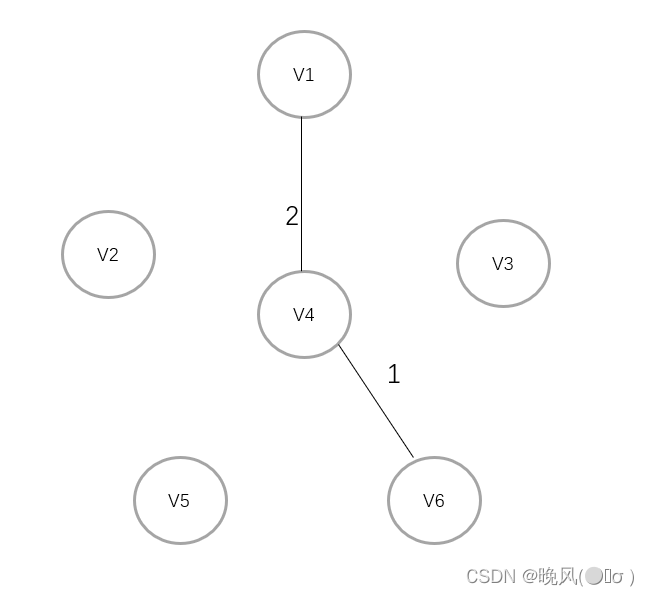
此时邻接的边的权值分别为3、4,以及加上前面的3、6、4、5、5,即[3、4、4、5、5、6],取最小权值3,V6与邻接的顶点V5相连:
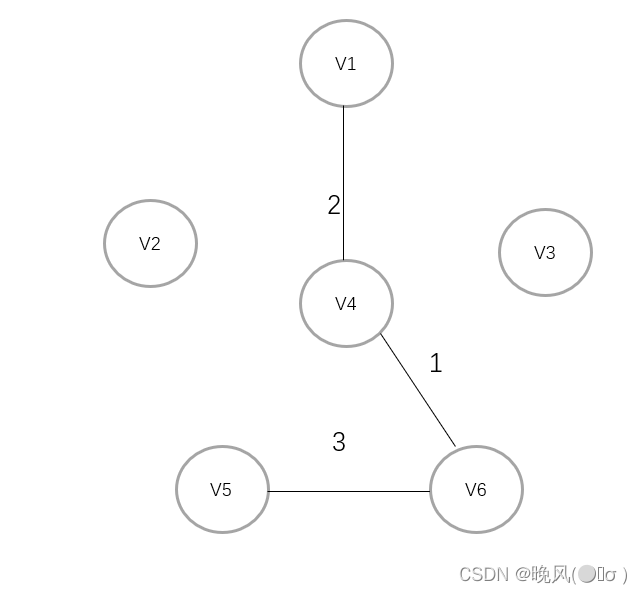
取此时最小权值,取的是当前图中剩余各边对应权值中最小的权值,即3,V1与V3相连:
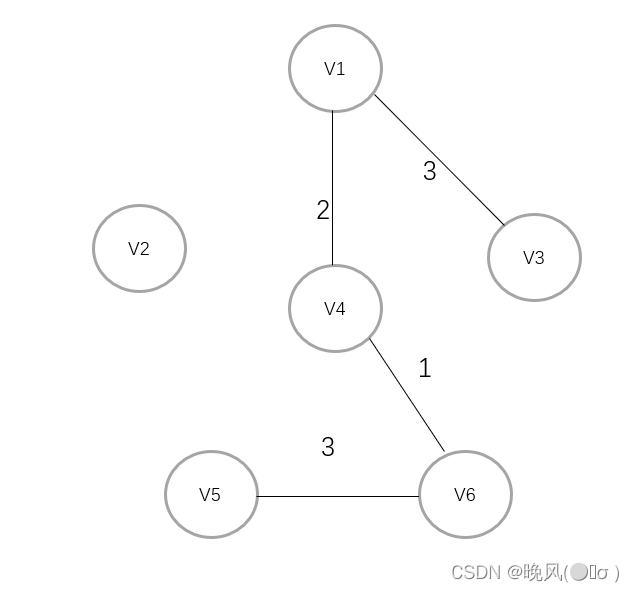
取此时最小权值,即4,V4与V2相连,至此所有顶点都被访问到,得到最小生成树(该最小生成树的代价为3+1+4+2+3=13):
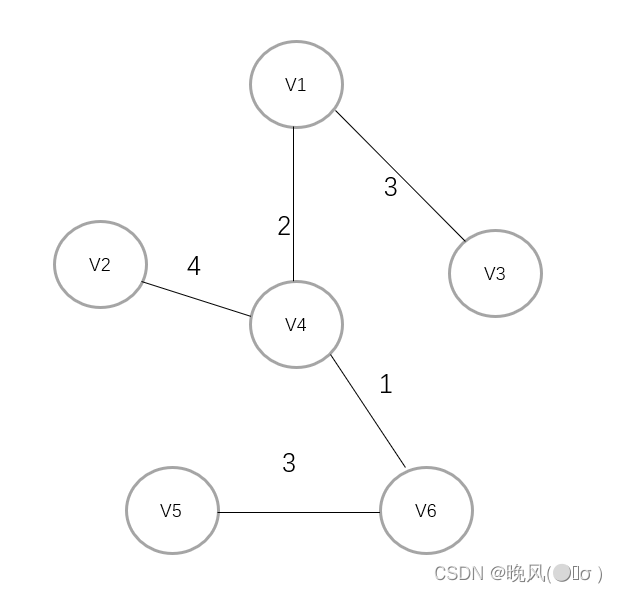
(1)普里姆算法的最优子结构性质
- 从上可看出,普里姆算法的核心是每次选择当前顶点(连通)与剩下顶点(未连通)之间的最小权值的边,依次进行,每次选最小,最后得到一棵最小生成树。
由于每次选择两个最小权值边,从而构成了一个局部最优解。【局部最优】
(2)普里姆算法的贪心选择性质
- 由于在每次选择中,都是选择的权值最小的边,所以保证了
每一步的选择情况都是当前最优的,从而最终得到的是一棵最小生成树。【选择最优】
2、克鲁斯卡尔算法(Kruskal)
克鲁斯卡尔算法的步骤如下:
①先将图的所有边对应的权值按照从小到大的顺序排序;
②选择其中权值最小的边加入并连接,并入树中,若选取的某边与先前的树构成回路(环),则舍去;
③一直进行下去,权值以小到大,直到所有顶点被访问到,得到最小生成树。
- 克鲁斯卡尔算法适用于求
边稀疏的网的最小生成树,核心语句是将e条边从小到大依次排序,所以n个顶点、e条边的无向连通带权图,其时间复杂度为O(eloge)。
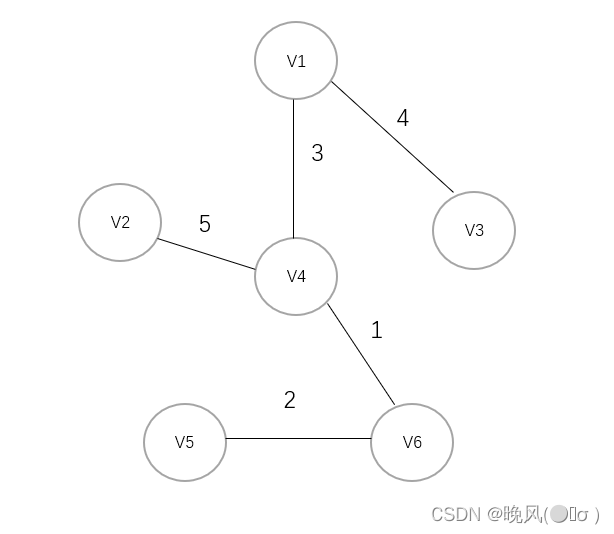
例如,下面是一个无向带权连通图,采用克鲁斯卡尔算法生成最小生成树:
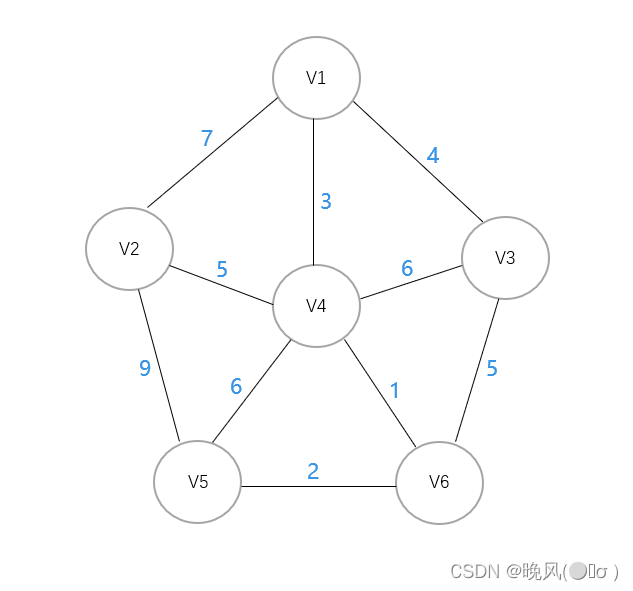
将图中所有边对应的权值,按从小到大排序如下:1,2,3,4,5,6,8。
可知权值1最小,首先连接V4和V6:
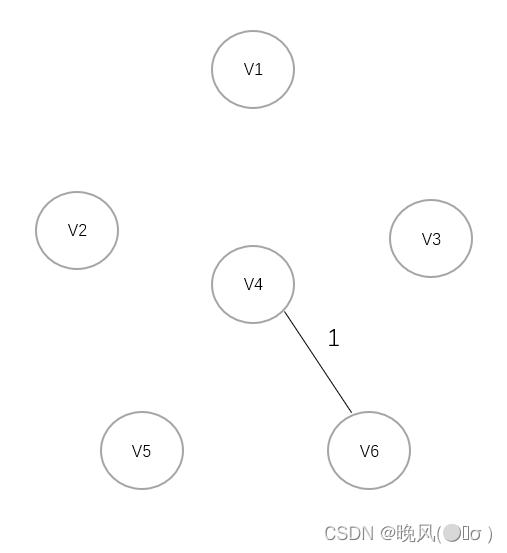
3、选择权值2,连接V6与V5:
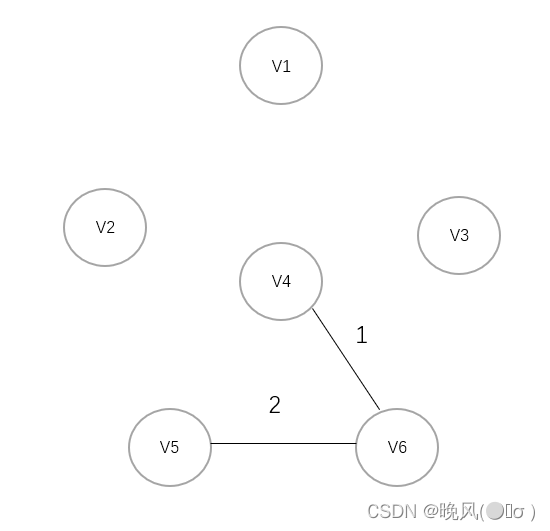
3、选择权值3,选取V4与V1连接:
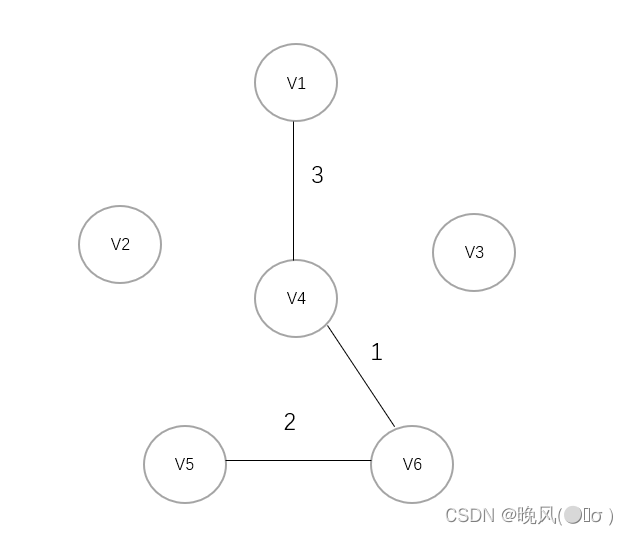
4、选择权值4,连接V1与V3:
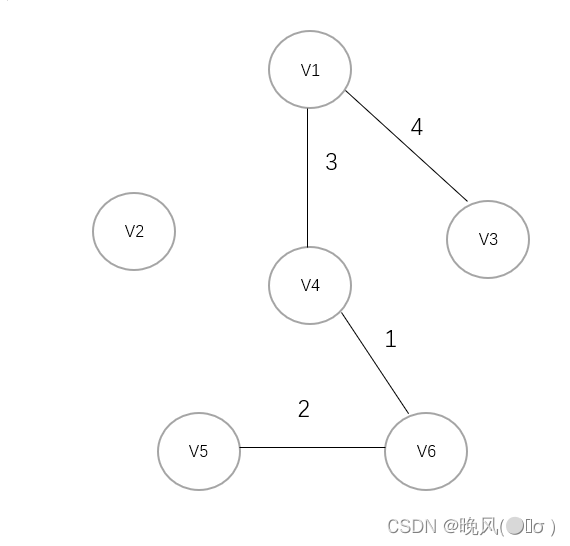
5、选取权值5,连接V4与V2,最终得到最小生成树如下(该最小生成树的代价为4+3+1+5+2=15):
(1)克鲁斯卡尔算法的最优子结构性质
- 克鲁斯卡尔算法中由于权值已经顺序排列,所以依次进行,每次加入的都是当前最小的边,构成的都是当前的一个连通分量的最小生成树(该顶点到其他顶点的最小生成树),最后得到整个图的最小生成树。
由于事先已排序好,每次选择的是当前最小权值边,从而构成了一个局部最优解。【局部最优】
(2)克鲁斯卡尔算法的贪心选择性质
- 由于在每次选择中,都是选择的权值最小的边且保证不会成回路(环),若不满足该条件,则说明当前情况不是最优,所以保证了在
每一步的选择情况都是当前最优的,从而最终得到的是一棵最小生成树。【选择最优】
3、两种算法的比较
| 名称 | 比较 |
|---|---|
| 普里姆算法 | 一次次 |
| 克鲁斯卡尔算法 | 整体 |
普里姆算法是每次选取一个最短边,即针对顶点,只能得到该顶点到其他顶点的最小生成树,当需要求图的最小生成树时,需要一次次的普里姆算法才能得到最小生成树,而克鲁斯卡尔算法由于一开始就将边的权值按从小到大依次排序,是从整体上出发,所以可以直接得到最小生成树,另外,由于需要对所有的边进行排序,其占用的空间也比普里姆算法多,空间复杂度为O(n)。
(三)图的应用——求单源最短路径
迪杰斯特拉算法(Dijkstra)
迪杰斯特拉算法计算的是在一个有向带权图中,指定一个源点到其他所有顶点的最短路径长度,即最短路径,而单源最短路径一般通过迪杰斯特拉算法解决。
在带权图中,一个顶点到另一个顶点所经过边的权值之和称为该路径的带权路径长度,由于可能路径不止一条,所以将带权路径长度最短的那条路径称为最短路径。
迪杰斯特拉算法的步骤如下:
①通过一个数组存储源点到每个顶点的距离;
②依次选取源点当前未访问到的所有顶点中距离最短的顶点,然后更新该顶点相邻的顶点与源点的距离;
③重复过程,直到所有顶点都被访问到。
- 克鲁斯卡尔算法中的核心语句是寻找距离源点最近的顶点,所以n个顶点的有向带权图,其
时间复杂度为O(n2),另外由于需要数组存放带权邻接矩阵,所以空间复杂度为O(n)。
(1)迪杰斯特拉算法的最优子结构性质
- 在每次更新该顶点相邻的顶点与源点的距离时,
当前所有的顶点与源点的最短路径是最优的,从而构成了一个局部最优解。【局部最优】
(2)迪杰斯特拉算法的贪心选择性质
- 由于每次选择的都是源点当前未访问到的所有顶点中距离最短的顶点,
保证选择的都是当前距离最短,从而得到的是最短路径。【选择最优】
相关文章:

数据结构与算法设计分析——贪心算法的应用
目录 一、贪心算法的定义二、贪心算法的基本步骤三、贪心算法的性质(一)最优子结构性质(二)贪心选择性质 四、贪心算法的应用(一)哈夫曼树——哈夫曼编码(二)图的应用——求最小生成…...

Leetcode 2895. Minimum Processing Time
Leetcode 2895. Minimum Processing Time 1. 解题思路2. 代码实现 题目链接:2895. Minimum Processing Time 1. 解题思路 这一题整体上来说其实没啥难度,就是一个greedy算法,只需要想明白耗时长的任务一定要优先执行,不存在某个…...

学信息系统项目管理师第4版系列21_范围管理
1. 产品范围 1.1. 某项产品、服务或成果所具有的特征和功能 1.2. 产品范围的完成情况是根据产品需求来衡量的 1.3. “需求”是指根据特定协议或其他强制性规范,产品、服务或成果必须具备的条件或能力 2. 项目范围 2.1. 包括产品范围,是为交付具有规…...

threejs 透明贴图,模型透明,白边
问题 使用Threejs加载模型时,模型出现了上面的问题。模型边缘部分白边,或者模型出现透明问题。 原因 出现这种问题是模型制作时使用了透明贴图。threejs无法直接处理贴图。 解决 场景一 模型有多个贴图时(一个透贴和其他贴图࿰…...

CCF CSP认证 历年题目自练Day21
题目一 试题编号: 201909-1 试题名称: 小明种苹果 时间限制: 2.0s 内存限制: 512.0MB 题目分析(个人理解) 先看输入,第一行输入苹果的棵树n和每一次掉的苹果数m还是先如何存的问题…...
【Python_PySide2学习笔记(十六)】多行文本框QPlainTextEdit类的的基本用法
多行文本框QPlainTextEdit类的的基本用法 前言正文1、创建多行文本框2、多行文本框获取文本3、多行文本框获取选中文本4、多行文本框设置提示5、多行文本框设置文本6、多行文本框在末尾添加文本7、多行文本框在光标处插入文本8、多行文本框清空文本9、多行文本框拷贝文本到剪贴…...
linux上negix部署静态页面
1.看配置文件 进入cndf.d 这里的是配置部署项目中的文件 进入一个查看下 上面的是服务的域名,服务是http://test.fun-med.cn/#/,后面加服务名(你的前端) 2.看下页面位置 和上面的路径要匹配...

41.说说Promise自身的静态方法
41.说说Promise自身的静态方法 Promise.all (有一个失败就失败,所有的都成功就成功)Promise.race (有一个成功就成功,有一个失败就失败)Promise.allSettled (所有的异步操作执行完毕之后&#…...

通讯网关软件019——利用CommGate X2OPCUA实现OPC UA访问Oracle服务器
本文介绍利用CommGate X2OPCUA实现OPC UA访问ORACLE数据库。CommGate X2OPCUA是宁波科安网信开发的网关软件,软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示,实现上位机通过OPC UA来获取ORACLE数据库的数据。 【解决方案】…...
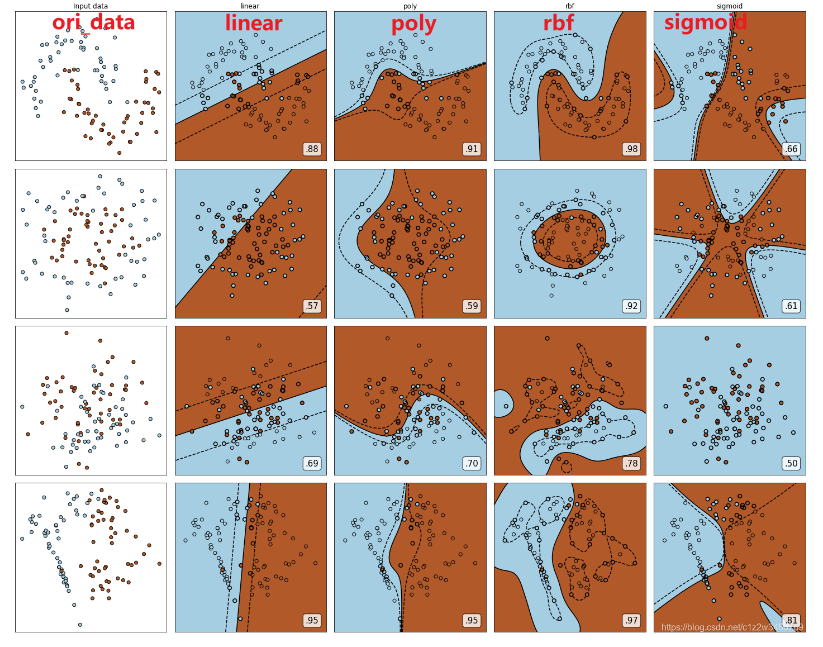
【机器学习】svm
参考 sklearn中SVC中的参数说明与常用函数_sklearn svc参数-CSDN博客https://blog.csdn.net/transformed/article/details/90437821 参考PYthon 教你怎么选择SVM的核函数kernel及案例分析_clfsvm.svc(kernel)-CSDN博客https://blog.csdn.net/c1z2w3456789/article/details/10…...
基于SSM+Vue的学习交流论坛的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用Vue技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

开发与运营:“开发”和“运营”角色有何不同和重叠?
开发和运营是促进软件系统交付的两种角色。大多数大规模构建软件的组织都会雇用这两个学科的人员。不过,开发和运维并不是完全孤立的。团队重叠并实现更高的吞吐量是很常见的。 在本文中,您将学习区分开发人员和操作人员之间的主要区别,以及它们重叠的方式。尽管有将两者结合…...

关于GD32引脚PA13、PA15、PB3、PB4配置为普通引脚的问题
关于GD32引脚PA13、PA15、PB3、PB4配置为普通引脚的问题 在实际开发中,经常会遇到引脚资源受限需要将一些具有特定功能的引脚配置为普通引脚或其他引脚功能使用的情况。 博主之前遇到过类似的情况,都正常解决了。但偶尔也会出现在配置引脚时少了一些配…...

JS-Dom转为图片,并放入pdf中进行下载
1、将dom转换为图片 这里我们使用html2canvas工具插件先将dom转为canvas元素然后canvas拥有一个方法可以将绘制出来的图形转为url然后下载即可注意:如果元素使用了渐变背景并透明的话,生成的图片可能会有点问题。我下面这个案例使用了渐变背景实现元素对…...
Python 无废话-办公自动化Excel格式美化
设置字体 在使用openpyxl 处理excel 设置格式,需要导入Font类,设置Font初始化参数,常见参数如下: 关键字参数 数据类型 描述 name 字符串 字体名称,如Calibri或Times New Roman size 整型 大小点数 bold …...

Python视频剪辑-Moviepy音频效果afx方法
随着多媒体内容在日常生活和工作中的广泛应用,音频处理成为了一个越来越重要的技能。无论是在游戏开发、音乐制作,还是在各种应用和网站中,高质量的音频处理都能极大地提升用户体验。然而音频处理看似复杂,实则不必如此。其实只需要掌握一些基础的概念和技巧,就能够完成大…...

让LLM模型输入token无限长
背景 增加LLM的输入token已经有很多的研究,但是思路无外乎:模型抽取局部特征通过上层通过模型融合预测最终解,以及这个思路的一些变种。然而这些思路其实都没能很彻底的解决无限长token问题,根据《EFFICIENT STREAMING LANGUAGE …...
RabbitMQ 介绍与 SpringBootAMQP使用
一、MQ概述 异步通信的优点: 耦合度低吞吐量提升故障隔离流量削峰 异步通信的缺点: 依赖于Broker的可靠性、安全性、吞吐能力架构复杂,业务么有明显的流程线,不方便追踪管理 什么是的MQ MQ(Message Queue…...

企业门户的必备选择,WorkPlus的定制化解决方案
在当今数字化时代,企业门户成为了企业内外沟通与协作的重要基础设施。WorkPlus作为领先的品牌,为企业提供了一站式的企业门户解决方案,旨在提升企业形象、改善内外部沟通与协作效率。本文将深入探讨WorkPlus如何通过定制化的设计,…...

基于maven的项目搭建(已跑通)
1、直接选择archetype-webapp即可 (这里很多人会觉得很慢–解决方案:https://blog.csdn.net/qq_45591895/article/details/133705674?spm1001.2014.3001.5501) 2、手动添加一个java目录即可。 3、添加Tomcat 3、这就跑通了,可以…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
