【网络安全 --- kali2023安装】超详细的kali2023安装教程(提供镜像资源)
如果你还没有安装vmware 虚拟机,请参考下面博客安装
【网络安全 --- 工具安装】VMware 16.0 详细安装过程(提供资源)-CSDN博客【网络安全 --- 工具安装】VMware 16.0 详细安装过程(提供资源)https://blog.csdn.net/m0_67844671/article/details/133609717?spm=1001.2014.3001.5502
一,资源下载
百度网盘镜像下载链接:
百度网盘 请输入提取码百度网盘为您提供文件的网络备份、同步和分享服务。空间大、速度快、安全稳固,支持教育网加速,支持手机端。注册使用百度网盘即可享受免费存储空间![]() https://pan.baidu.com/s/1H_U0Y2wFQVgN-eZ7Ms-r-w?pwd=8888提取码:8888
https://pan.baidu.com/s/1H_U0Y2wFQVgN-eZ7Ms-r-w?pwd=8888提取码:8888
二,系统安装
2-1 系统安装
kali系统经常更新,所以可以选择最新版本下载下来玩,网址:
Index of /kali-weekly![]() https://cdimage.kali.org/kali-weekly/
https://cdimage.kali.org/kali-weekly/
自己下载也可以,用我给大伙准备的也可以,从百度网盘里下载
1,准备好镜像,我给大家准备好了,从百度网盘下载即可
![]()
2,打开VMware 虚拟机,点击新建虚拟机

3,选自定义,然后下一步

4,硬件兼容性15.X 或者16.X都可以,然后下一步

5,选择稍后安装操作系统,然后下一步
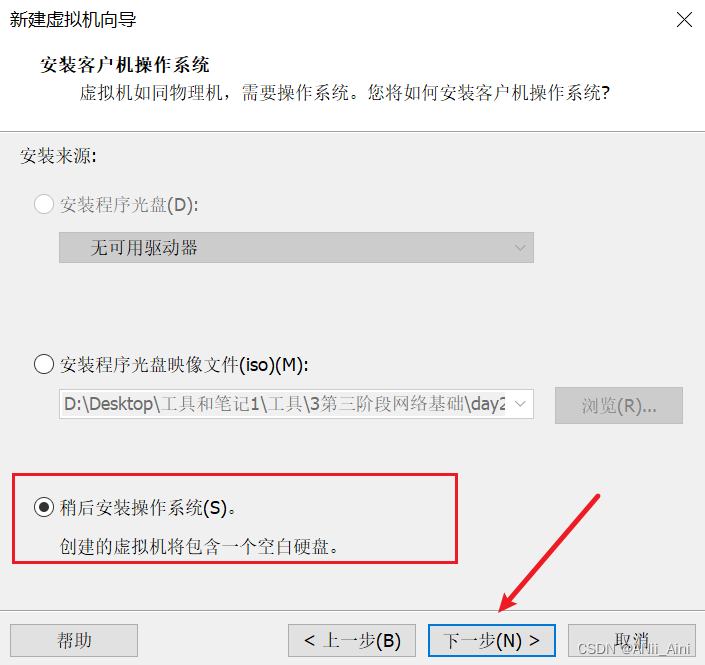
6,kali属于debian系列,选择Deban 6 64位,然后下一步

7,选择存放虚拟机的文件夹,然后下一步

8,每个处理器内核数量两个,如果你计算机内存很大,可以给多一点,4也可以,然后下一步

9,内存尽量大一点,我给了4G

10,网路选择桥接模式(这里的几个网路模式比较重要,抽空了解一下,绕不然遇到网络问题不知道咋回事儿)

11,默认即可,下一步

12,默认即可,下一步

13,默认即可,然后下一步

14,磁盘容量建议给大一点,如果你电脑剩余容量没那么大,给个30~40G也可以,不够了可以调的。

15,直接下一步
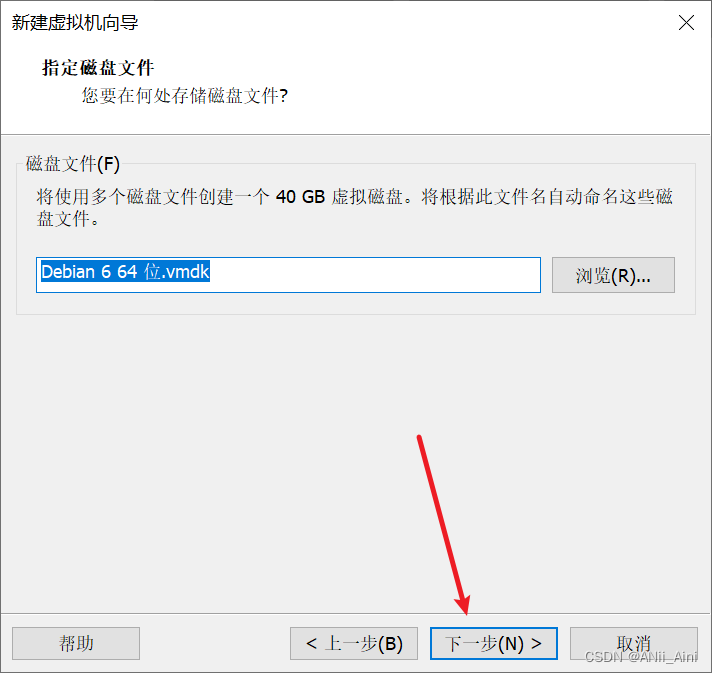
16,自定义硬件点进去

17,选择打印机,移除以后,点击关闭即可

18,点击完成

19,进入到编辑虚拟机设置里面

20,选择镜像文件,然后确定

21,然后就是开启此虚拟机

22,kali有桌面比较好,所以我们把桌面一起安装上,选择第一个,按回车

23,选择语言为中文,然后点击continue

24,下一步

25,选择汉语,然后下一步

26,稍微耐心等待

27,可以起个主机名,或者默认也可以,然后下一步

28,不同填写,继续下一步
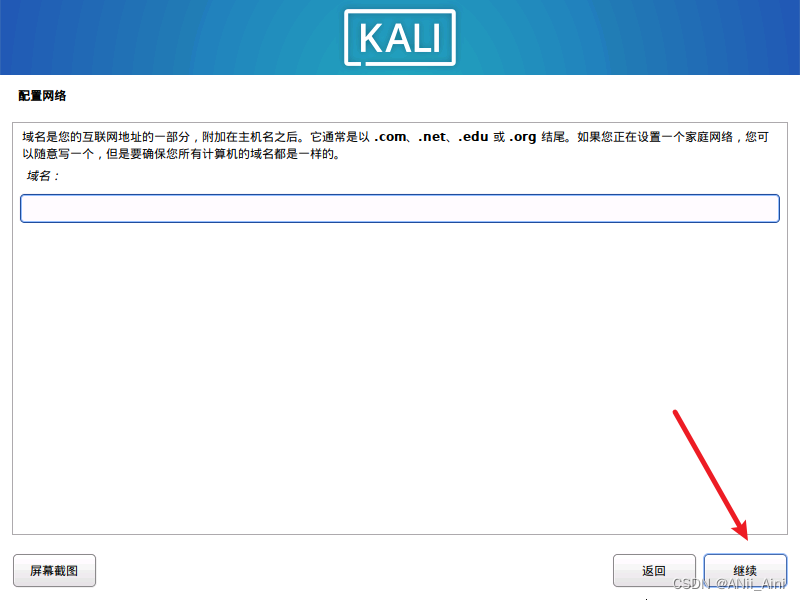
29,输入一个用户名

30,这里填写的是登录的用户名,千万不能忘记
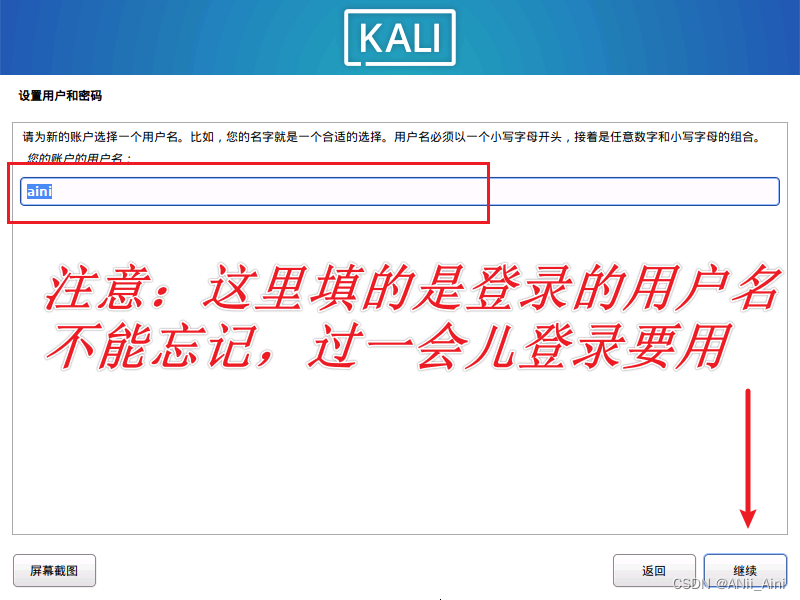
31,这里是密码,密码不能忘记,然后下一步

32,默认即可

33,默认即可

34,默认即可

35,默认即可,然后下一步

36,选择‘是’ ,然后下一步

37,耐心等待,等其配置完成

38,默认即可,然后下一步

39,继续等待,等其安装完(时间比较长,差不多10分钟左右)

40,选择是 ,然后继续

41,选择 /dev/sda 然后继续

42,等待一会儿,让系统安装完成
43,安装完成,点击继续

44,输入安装时设置的账号密码登录即可

45,这就是kali2023的桌面了

46,检查有没有网路 (鼠标右击,打开终端)

47,在终端输入 ping baidu.com,看到确实能上网

48,检查VMware tools有没有安装好 ,如果在虚拟机菜单里有灰色的重新安装VMware tools字样,说明已经安装好了,若没有安装好,则点击安装VMware tools字样进行安装

2-2 切换root用户
49,修改root密码,输入下面指令按回车
sudo passwd root

50,然后按两次回车,密码就设置完成了

51,切换到root用户
su root
su root 按回车以后按提示输入刚刚设置的面,就切换成功了

2-3 开启ssh远程连接服务
52,开启ssh远程连接服务 (可以用xshell等工具远程连接)
/etc/init.d/ssh start ## 启动ssh服务
/etc/init.d/ssh status ## 查看ssh服务状态,active表示已经开启

53,设置系统自启动
update-rc.d ssh enable ## 开机自启动,每次开机服务自动开启

2-4 xshell连接测试
54,xshell测试连接
xshell工具的下载,安装请参考下面这篇博客
【网络安全 --- 工具安装】Centos 7 详细安装过程及xshell,FTP等工具的安装(提供资源)_ANii_Aini的博客-CSDN博客【网络安全 --- 工具安装】详细讲解了,linux CentOS系统的详细安装过程,以及远程连接工具xshell的安装和FTP 文件上传工具的安装https://blog.csdn.net/m0_67844671/article/details/133616010?spm=1001.2014.3001.5502
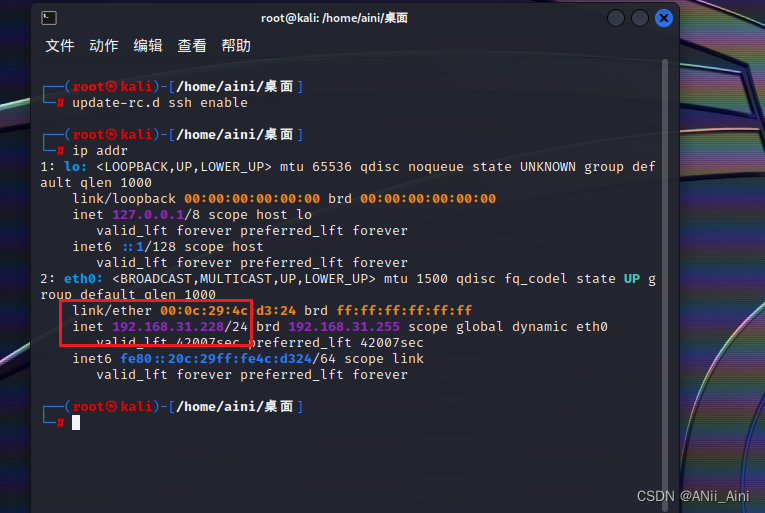
55,打开xshell工具
命令行连接,输入命令 ssh aini@192.168.31.228
(注意,远程不能直接以root用户身份连接,所以先以普通用户身份连接,在切换到root用户)
我们安装的时候指定的用户名和密码就是普通用户
56,接受并保存

57,输入密码即可
已经以普通用户的身份连接上了

58,切换到root用户
su root
然后按提示输入密码即可

就这样kali2023系统已经配置安装好了
如果还要安装别的系统关注我,我会出详细的安装各种系统的教程
如果想要学网络安全关注我,最近在做系统的网络安全博客,靶场,工具可免费提供
相关文章:

【网络安全 --- kali2023安装】超详细的kali2023安装教程(提供镜像资源)
如果你还没有安装vmware 虚拟机,请参考下面博客安装 【网络安全 --- 工具安装】VMware 16.0 详细安装过程(提供资源)-CSDN博客【网络安全 --- 工具安装】VMware 16.0 详细安装过程(提供资源)https://blog.csdn.net/m0…...
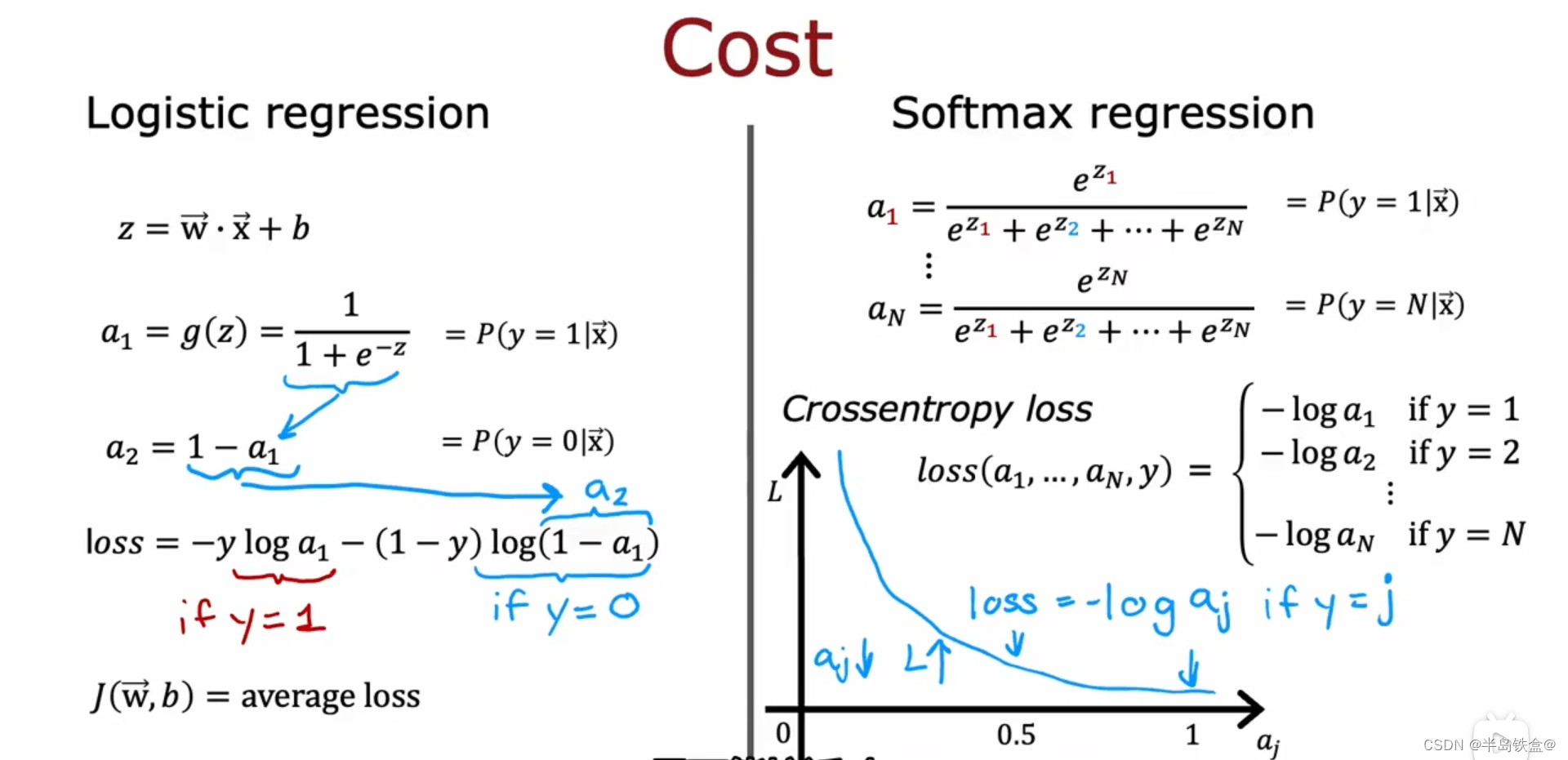
机器学习笔记(二)
过拟合 如下图左边,模型出现了过拟合现象 为了解决过拟合现象, 其中一个做法是多收集数据,如右图。 第二种做法是减少模型的特征数量,即x 第三种做法是正则化 正则化就是减少x前面的参数 w的数值, 不用消除x 正则化的梯度下降如下, 因为只是缩小了w的值,而 b的值保持不变 …...
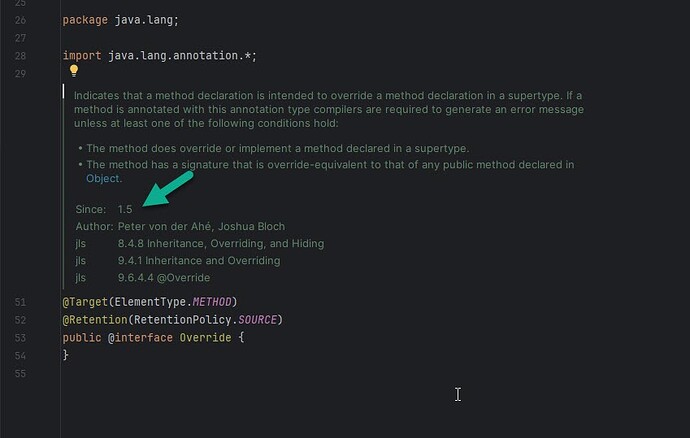
Java @Override 注解
在代码中,你可能会看到大量的 Override 注解。 这个注解简单来说就是让编译器去读的,能够避免你在写代码的时候犯一些低级的拼写错误。 Java Override 注解用来指定方法重写(Override),只能修饰方法并且只能用于方法…...

用rabbitMq 怎么处理“延迟消息队列”?
延迟消息队列是一种允许消息在发送后等待一段时间,然后再被消费的机制。这种机制通常用于需要延迟处理的应用场景,如定时任务、消息重试、消息调度等。在 RabbitMQ 中,实现延迟消息队列需要使用一些额外的组件和技术,因为 RabbitM…...

不常见的JS加密分析
前言 今天发现一个很少见的JS加密代码,他由一段十分少见的环境检测逻辑,修改一个字符都会被检测到,十分神奇,今天献上。 源代码 let hiJsJiami;!function(){const Zg3GArray.prototype.slice.call(arguments);return eval(&…...

TCP原理特性详解
文章目录 可靠传输机制1.确认应答2.超时重传2.连接管理1.三次握手2.四次挥手 传输效率1.滑动窗口2.流量控制3.拥塞控制4.延时应答5.捎带应答 面向字节流粘包问题 TCP异常情况 可靠传输机制 可靠性:即发送方知道数据是发送成功了,还是失败了。 1.确认应答…...

什么是懒加载,JS如何实现懒加载,在php中如何去实现懒加载
懒加载(Lazy Loading)是一种前端优化技术,用于推迟加载页面中的某些资源(如图片、脚本、样式等),直到用户需要访问或者接近该资源时才进行加载。这可以减少初始页面加载时间,并提高页面性能和用…...

Cesium 展示——读取文件——加载 geojson 文件数据
文章目录 需求分析方法一:加载 geojson 文件方法二:加载 后台解析后的 geojson 文件结果需求 在做项目时,对加载 geojson 格式的数据有了一定的了解,因此试着尝试接手后台解析的 geojson 数据进行绘制,因此做了总结如下 分析 方法一:加载 geojson 文件 this.od6 = wi…...
Apache log4net™ 手册 - 配置)
(二)Apache log4net™ 手册 - 配置
0、引言 在上一篇文章中我们简单介绍了 Log4Net 及其核心的三大组件。本文将在上一篇文章的基础上继续探讨与 Log4Net 配置相关的内容。 1、配置 将日志请求插入到应用程序代码中需要进行大量的计划和工作。观察表明,大约4%的代码专门用于日志记录。因此…...

Elasticsearch:时间点 API
Elasticsearch:时间点 API-CSDN博客 在今天的文章中,我将着重介绍 Point in time API。在接下来的文章中,我将介绍如何运用 PIT 来对搜索结果进行分页。这也是被推荐使用的方法。 Point in time API 默认情况下,搜索请求针对目标…...

hive数据表定义
分隔符 CREATE TABLE emp( userid bigint, emp_name array<string>, emp_date map<string,date>, other_info struct<deptname:string, gender:string>) ROW FORMAT DELIMITED FIELDS TERMINATED BY \t COLLECTION ITEMS TERMINATED BY , MAP KEYS TERMINAT…...

OpenMesh 网格简化之顶点聚类
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 顶点聚类方法将落在给定大小体素中的所有顶点集中到单个顶点之上,其过程有点类似于点云体素下采样,之后再基于聚类之后的顶点重新连接面片,以达到网格简化的目的。 二、实现代码 #define _USE_MATH_DEFINES #in…...

C++ 类和对象篇(八) const成员函数和取地址运算符重载
目录 一、const成员函数 1. const成员函数是什么? 2. 为什么有const成员函数? 3. 什么时候需要使用const修饰成员函数? 二、取地址运算符重载 1. 为什么需要重载取地址运算符? 2. 默认取地址运算符重载函数 3. 默认const取地址运…...

k8s 集群安装(vagrant + virtualbox + CentOS8)
主机环境:windows 11 k8s版本:v1.25 dashboard版本:v2.7.0 calico版本: v3.26.1 CentOS8版本:4.18.0-348.7.1.el8_5.x86_64 用到的脚本: https://gitcode.net/sundongsdu/k8s_cluster 1. Vagrant创建…...
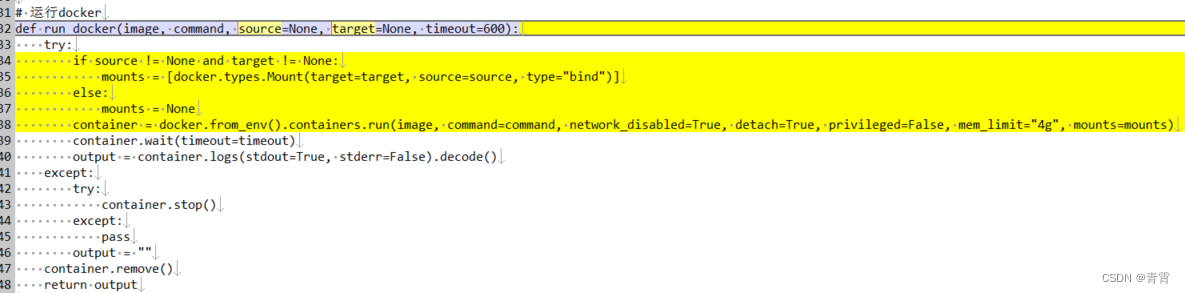
8、Docker数据卷与数据卷容器
一、数据卷(Data Volumes) 为了很好的实现数据保存和数据共享,Docker提出了Volume这个概念,简单的说就是绕过默认的联合文件系统,而以正常的文件或者目录的形式存在于宿主机上。又被称作数据卷。 数据卷 是一个可供一个或多个容器使用的特殊目…...
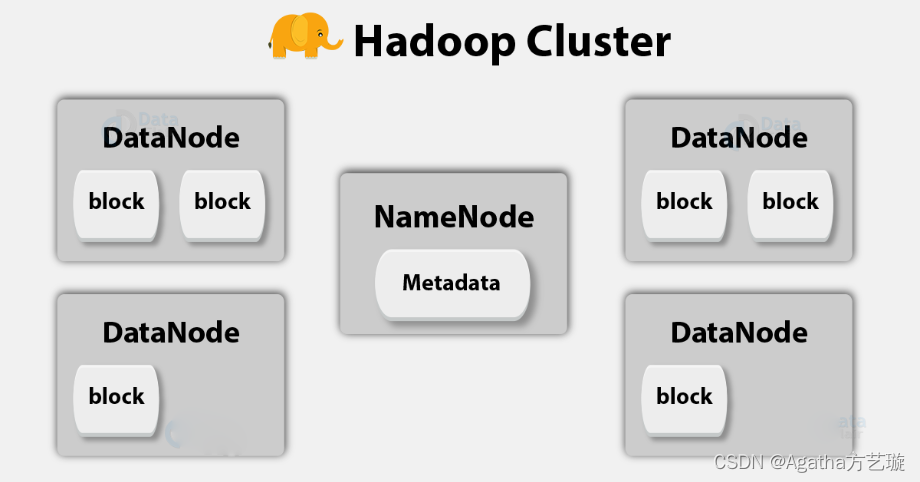
大数据与Hadoop入门理论
一、大数据的3种数据类型 1、结构化数据 可定义,有类型、格式、结构的强制约束 如:RDBMS(关系型数据库管理系统) 2、非结构化数据 没有规律没有数据约束可言,很复杂难以解析 如:文本文件,视…...

持续集成部署-k8s-深入了解 Pod:探针
持续集成部署-k8s-深入了解 Pod:探针 1. 探针分类2. 探针探测方式3. 探针参数配置4. 启动探针的应用5. Liveness 探针的应用6. Readiness 探针的应用1. 探针分类 Kubernetes 中的探针是指容器内的进程用于告知 Kubernetes 组件其自身状态的机制; Readiness Probe:就绪探针用…...
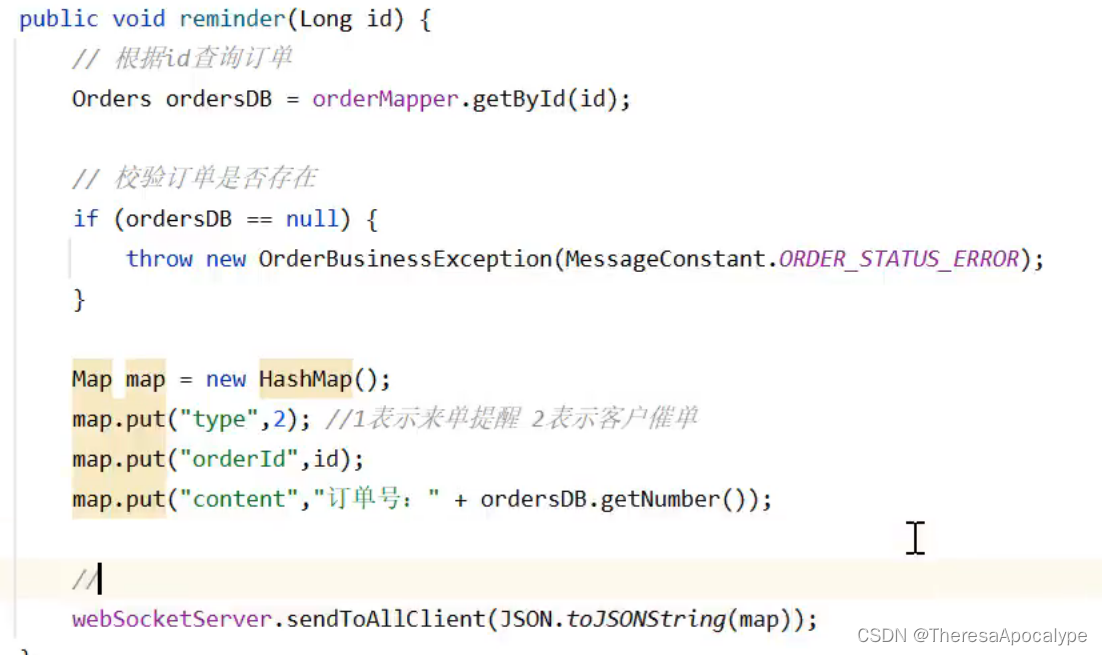
来单提醒/客户催单 ----苍穹外卖day9
来单提醒 需求分析 代码开发 注意:前端请求的并不是8080端口;而是先请求Nginx,Nginx进行反向代理以后转发到8080端口 这段代码首先创建了一个orders类用于更新订单状态 并且在更新状态后使用websocket发送给后端提醒 将信息放在map后,使用json的string化方式传给一个接收对象,…...
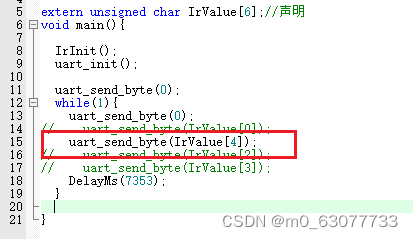
【单片机】18-红外线遥控
一、红外遥控背景知识 1.人机界面 (1)当面操作:按键,旋转/触摸按键,触摸屏 (2)遥控操作:红外遥控,433M/2.4G无线通信【穿墙能力强】,蓝牙-WIFI-Zigbee-LoRa等…...

【Node.js】module 模块化
认识 node.js Node.js 是一个独立的 JavaScript 运行环境,能独立执行 JS 代码,可以用来编写服务器后端的应用程序。基于Chrome V8 引擎封装,但是没有 DOM 和 BOM。Node.js 没有图形化界面。node -v 检查是否安装成功。node index.js 执行该文…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
