【随想】每日两题Day.12(实则一题)
题目:15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
代码:
class Solution {public List<List<Integer>> threeSum(int[] nums) {List<List<Integer>> res = new ArrayList<>();int left = 0;int right = 0;Arrays.sort(nums);for(int i = 0;i<nums.length;i++) {if(nums[i] > 0) return res;if(i>0 && nums[i]==nums[i-1]) continue;left = i+1;right = nums.length - 1;while(left < right) {int sum = nums[i] + nums[left] + nums[right];if(sum > 0) {right--;}else if(sum < 0) {left++;}else{res.add(Arrays.asList(nums[i],nums[left],nums[right]));//对b,c去重while(right>left && nums[left] == nums[left+1]) left++;while(right>left && nums[right] == nums[right-1]) right--;left++;right--;}}}return res;}
}思考:
此题难度不小,在日后复习要多敲代码反复品味。思考部分有待补充
相关文章:
)
【随想】每日两题Day.12(实则一题)
题目:15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不…...
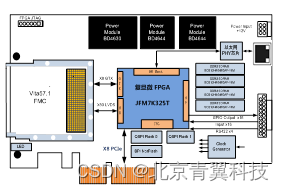
基于复旦微JFM7K325T FPGA的高性能PCIe总线数据预处理载板(100%国产化)
PCIE711是一款基于PCIE总线架构的高性能数据预处理FMC载板,板卡采用复旦微的JFM7K325T FPGA作为实时处理器,实现各个接口之间的互联。该板卡可以实现100%国产化。 板卡具有1个FMC(HPC)接口,1路PCIe x8主机接口&#x…...

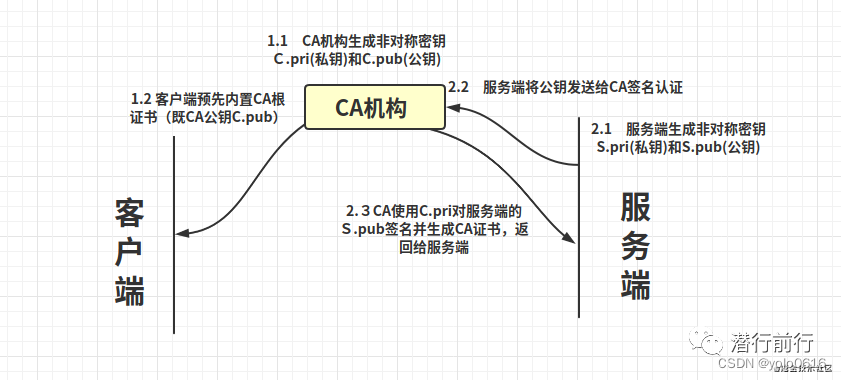
什么是原型链(prototype chain)?如何实现继承?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

RabbitMQ 5种工作模式介绍和Springboot具体实现
RabbitMQ有5中工作模式:简单模式、工作队列模式、发布/订阅模式、路由模式和主题模式 简单模式(Simple Mode) 简单模式是最基本的工作模式,也是最简单的模式。在简单模式中,生产者将消息发送到一个队列中,…...

C++ - 可变模版参数 - emplace相关接口函数 - 移动构造函数 和 移动赋值运算符重载 的 默认成员函数
可变模版参数 我们先来了解一下,可变参数。可变参数就是在定义函数的时候,某一个参数位置使用 "..." 的方式来写的,在库当中有一个经典的函数系列就是用的 可变参数:printf()系列就是用的可变参…...
总结三:计算机网络面经
文章目录 1、简述静态路由和动态路由?2、说说有哪些路由协议,都是如何更新的?3、简述域名解析过程,本机如何干预域名解析?4、简述 DNS 查询服务器的基本流程是什么?DNS 劫持是什么?5、简述网关的…...

服务器数据恢复-VMWARE ESX SERVER虚拟机数据恢复案例
服务器数据恢复环境: 几台VMware ESX SERVER共享一台某品牌存储,共有几十组虚拟机。 服务器故障: 虚拟机在工作过程中突然被发现不可用,管理员将设备进行了重启,重启后虚拟机依然不可用,虚拟磁盘丢失&#…...

COCI 2021-2022 #1 - Set 题解
思路 我们将原题中的数的每一位减一,此时问题等价。 下面的异或都是在三进制下的异或。(相当于不进位的加法) 我们考虑原题中的条件,对于每一位,如果相同,则异或值为 0 0 0,如果为 1 1 1&a…...

分享40个极具商业价值的chatGPT提问prompt
原文:分享40个极具商业价值的chatGPT提问prompt | 秋天的童话博客 1、分析并改善定价策略 提示: "分析我当前的[插入产品或服务]定价策略。提出改进建议,并帮助我制定新的定价策略,以最大化利润和客户满意度。" Analyze and Imp…...

一文搞懂到底什么是元宇宙
一、背景 2021年,“元宇宙”是科技界的开端。 2021”元宇宙”这个词在Facebook更名后被点燃了,无疑是21世纪科技界最爆的起点。各式各样的定义、解读都出现了,有人说它是炒作,甚至是骗局,但也有人说它就是互联网的未…...

【重拾C语言】六、批量数据组织(四)线性表—栈和队列
目录 前言 六、批量数据组织——数组 6.1~3 数组基础知识 6.4 线性表——分类与检索 6.5~7 数组初值;字符串、字符数组、字符串数组;类型定义 typedef 6.8 线性表—栈和队列 6.8.1 栈(Stack) 全局变量 isEmpty() isFull…...

力扣刷题-哈希表-一个字符串是否能够由另一个字符串中的字符组成
383 赎金信 给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字符只能在 ransomNote 中使用一次。ransomNote 和 magazin…...

Android使用AOP切面编程
在Android应用程序中,AOP可以被用于许多不同的场景,例如日志记录、权限控制、性能分析等。下面是一个简单的例子,说明如何在Android应用程序中使用AOP切面编程。 首先,我们需要在应用程序中引入AspectJ库。我们可以使用Gradle来完…...

Flutter学习笔记
此篇文章用来记录学习Flutter 和 Dart 相关知识 零.Dart基本数据类型 Dart 是一种静态类型的编程语言,它提供了一系列基本数据类型,用于存储和操作不同种类的数据。以下是 Dart 中的一些基本数据类型以及它们的详细介绍: 1. 整数类型&#…...

软件生命周期中的概念设计和详细设计的主要任务是什么
基础概念 在软件生命周期中,概念设计和详细设计是软件设计阶段中的两个重要环节。 概念设计阶段的主要任务是从业务需求出发,将系统的基本概念、主要功能和关键特性进行抽象和定义。概念设计旨在确定系统的整体架构和关键模块,包括以下主要…...
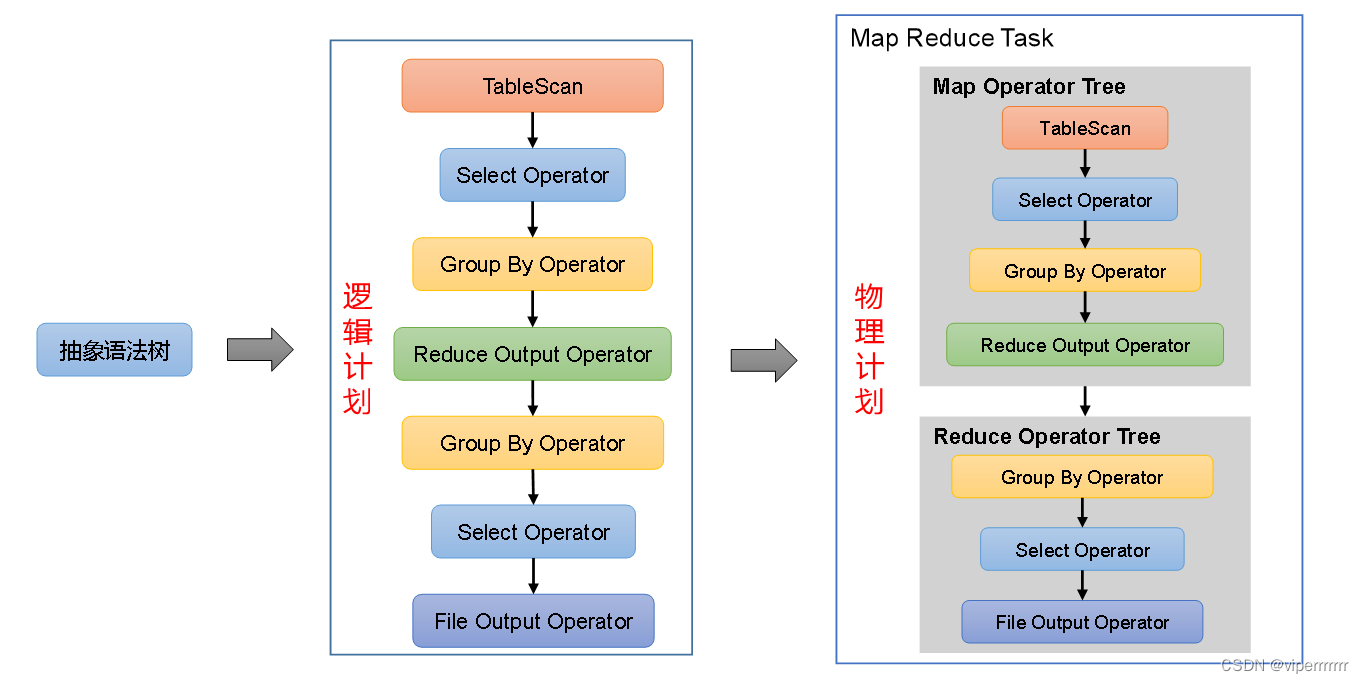
大数据学习(2)Hadoop-分布式资源计算hive(1)
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博>主哦&#x…...

深入探究HTML表单与JavaScript的关系
深入探究HTML表单与JavaScript的关系 引言 HTML表单是网页中数据收集的重要工具,而JavaScript则充当着这些数据的处理者和控制者的角色。二者之间的关系非常紧密,共同构成了现代Web应用中用户交互的基础。在这篇博客中,我们将详细地解析HTM…...
关于Jupyter notebook 创建python3 时进去不能重命名问题及不能编程问题
首先写这篇博客时,已经被这个问题折磨了三天,看了很多博客,其实解决这个问题的关键就是要么没有下pyzmq或者等级太高,要么等级太低,首先我会按照我思路来。 问题如图: 1.自动换行 2.不能重命名 我的解决办…...

一些可以用代码绘制流程图的工具
代码绘制流程图的工具有很多,以下是一些常用的工具: Mermaid:Mermaid 是一个基于 Markdown 的图表语言,可以生成各种类型的图表,包括流程图、时序图、甘特图等。Mermaid 可以使用 JavaScript 或 TypeScript 进行编写,可以通过 Node.js 运行。Graphviz:Graphviz 是一个开…...
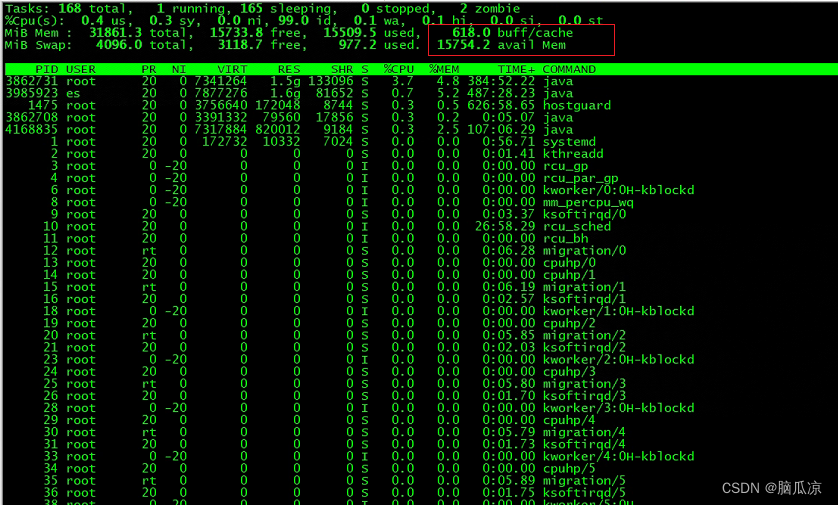
Centos中清除因程序异常终止,导致的残留的Cache/buff_drop_caches命令---linux工作笔记063
我这里因为nifi程序背压设置的不合理,导致,内存和CPU消耗过高,系统崩溃,但是重启NIFI以后,发现 对应的执行top命令,看到,系统的buff/cache 依然没有减少,说明内存被浪费了,残留在这里没有被回收. 用这个办法执行这个命令; linux会自动触发清理,但是只有在内存不够用的时候才会…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
