Vue中的router路由的介绍(快速入门)
路由的介绍
文章目录
- 路由的介绍
- 1、VueRouter的介绍
- 2、VueRouter的使用(5+2)
- 2.1、5个基础步骤(固定)
- 2.2、两个核心步骤
- 3、组件存放的目录(组件分类)
生活中的路由:设备和ip的映射关系(路由器)
Vue中路由:路径和组件的映射关系
1、VueRouter的介绍
作用:修改地址栏路径时,切换显示匹配的组件
说明:Vue官方的一个路由插件,是一个第三方包
官网:https://v3.router.vuejs.org/zh/
2、VueRouter的使用(5+2)
2.1、5个基础步骤(固定)
-
下载:下载 VueRouter模块到当前工程,版本3.6.5(Vue2对应的版本)
yarn add vue-router@3.6.5 -
引入
import VueRouter from 'vue-router' -
安装注册
Vue.use(vueRouter) -
创建路由对象
const router = new VueRouter() -
注入,将路由对象注入到new Vue实例中,建立关联
new Vue({ render: h =>h(App),router }).$mount( ' #app ')注入vueter对象之后:
Vue版本对应关系:
Vue2: VueRouter3.x Vuex3.x
Vue3: VueRouter4.x Vuex4.x
2.2、两个核心步骤
- 创建需要的组件(views目录),配路由规则

- 准备导航链接,配置路由出口(匹配的组件展示的位置)

3、组件存放的目录(组件分类)
vue文件本质无区别。路由相关的组件,为什么放在views目录呢?
-
组件分类:
.vue文件分2类:页面组件&复用组件(更易维护) -
src/views文件夹
- 页面组件–页面展示–配合路由用
-
src/components文件夹
- 复用组件–展示数据–常用于复用
文章推荐:Vue路由进阶–VueRouter声明式导航
相关文章:

Vue中的router路由的介绍(快速入门)
路由的介绍 文章目录 路由的介绍1、VueRouter的介绍2、VueRouter的使用(52)2.1、5个基础步骤(固定)2.2、两个核心步骤 3、组件存放的目录(组件分类) 生活中的路由:设备和ip的映射关系(路由器) V…...

ESP-07S进行TCP 通信测试
一,TCP Server 为 AP 模式,TCP Client 为 Station 模式。 这里电脑pc作为TCP Server,ESP-07S作为TCP Client 。 二,电脑端配置。 1,开启热点。 2,转到“设置”,编辑热点信息。 3,关闭…...

如何找到新媒体矩阵中存在的问题?
随着数字媒体的发展,企业的新媒体矩阵已成为品牌推广和营销的重要手段之一。 然而,很多企业在搭建新媒体矩阵的过程中,往往会忽略一些问题,导致矩阵发展存在潜在风险,影响整个矩阵运营效果。 因此,找到目前…...

MongoDB-基本常用命令
基本常用命令 MongoDB常用命令a) 案例需求b) 数据库操作b.1) 选择和创建数据库b.2) 删除数据库 c) 集合操作c.1) 集合的显示创建c.2) 集合的隐式创建c.3) 集合的删除 d) 文档基本CRUDd.1) 文档的插入(1) 单个文档的插入(2) 批量插入 d.2) 文档的基本查询(1) 查询所有(2) 投影查…...

Linux 常用systemctl service 脚本
文章目录 1. jar 包部署 service 脚本2. nginx 服务安装 脚本3.artemis 服务安装脚本 1. jar 包部署 service 脚本 默认jdk 执行: [Service] Typesimple Userroot WorkingDirectory/opt/app/webserver ExecStart/usr/bin/java -Xms512m -Xss256k -jar /opt/app/we…...

flask-sqlalchemy实现读写分离完整版
1. 依赖版本: alembic==1.6.5 click==8.0.1 colorama==0.4.4 Flask==1.1.2 Flask-Migrate==2.7.0 Flask-Script==2.0.6 Flask-SQLAlchemy==2.4.4 greenlet==1.1.0 itsdangerous==2.0.1 Jinja2==3.0.1 Mako==1.1.4 MarkupSafe==2.0.1 protobuf==3.17.3 PyMySQL==1.0.2 python-…...
windows下在cmd和git bash中执行bash download.sh失败
cmd报错信息: 解决办法: win64-wget-1.21.4 安装软件wget,如下这是64位的包,解压后,下面有个wget.exe,拷贝到C:\Windows\System32、 然后打开cmd,执行wget -V 如上,有版本信息就O…...

rust流程控制
一、分支 (一)if 1.if 语法格式 if boolean_expression { }例子 fn main(){let num:i32 5;if num > 0 {println!("正数");} }条件表达式不需要用小括号。 条件表达式必须是bool类型。 2.if else 语法格式 if boolean_expression { } …...
虚拟机软件Parallels Desktop 19 mac功能介绍
Parallels Desktop 19 mac是一款虚拟机软件,它允许用户在Mac电脑上同时运行Windows、Linux和其他操作系统。Parallels Desktop提供了直观易用的界面,使用户可以轻松创建、配置和管理虚拟机。 PD19虚拟机软件具有快速启动和关闭虚拟机的能力,让…...

在工业机器视觉领域中应用钡铼技术有限公司的EtherCAT网关
钡铼技术有限公司作为一家专注于业物联网关、工业智能网关、边缘计算网关、ARM嵌入式工业计算机、PLC远程采集网关、Modbus转MQTT网关、OPC UA网关、BACnet网关路由器、Lora网关、工业4G边缘路由器、4G无线远程数据采集模块、4G DTU RTU、以太网远程IO模块、工业总线分布式I/O模…...

ssh指定的密钥协商方式以及Ansible的hosts文件修改密钥协商方式
一、首先你要知道用什么加密协商。 [WARNING]: Invalid characters were found in group names but not replaced, use -vvvv to see details 10.10.2.190 | UNREACHABLE! > {"changed": false,"msg": "Failed to connect to the host via ssh: U…...

NLP 项目:维基百科文章爬虫和分类【01】 - 语料库阅读器
自然语言处理是机器学习和人工智能的一个迷人领域。这篇博客文章启动了一个具体的 NLP 项目,涉及使用维基百科文章进行聚类、分类和知识提取。灵感和一般方法源自《Applied Text Analysis with Python》一书。 一、说明 该文是系列文章,揭示如何对爬取文…...

QT sqlite的简单用法
1、相关头文件 #include <QSqlDatabase> #include <QSqlError> #include <QSqlQuery> #include <QSqlRecord> #include <QSqlIndex> #include <QSqlField> #include <QFile> #include <QDebug> 2、数据库对象 QSqlDatabas…...
大模型部署手记(12)LLaMa2+Chinese-LLaMA-Plus-2-7B+Windows+text-gen+中文对话
1.简介: 组织机构:Meta(Facebook) 代码仓:https://github.com/facebookresearch/llama 模型:chinese-alpaca-2-7b-hf 下载:使用百度网盘下载 硬件环境:暗影精灵7Plus Windows版…...

C#导出本机Win32native dll
C# 使用 "3f/DllExport" 工具导出C风格的本机函数 [文 / 张赐荣] 首先,让我们来了解一下什么是争渡读屏软件,以及什么是争渡文本预处理API。争渡读屏软件是一款屏幕朗读软件,用于协助视力障碍人士操作电脑。 争渡文本预处理API是一…...
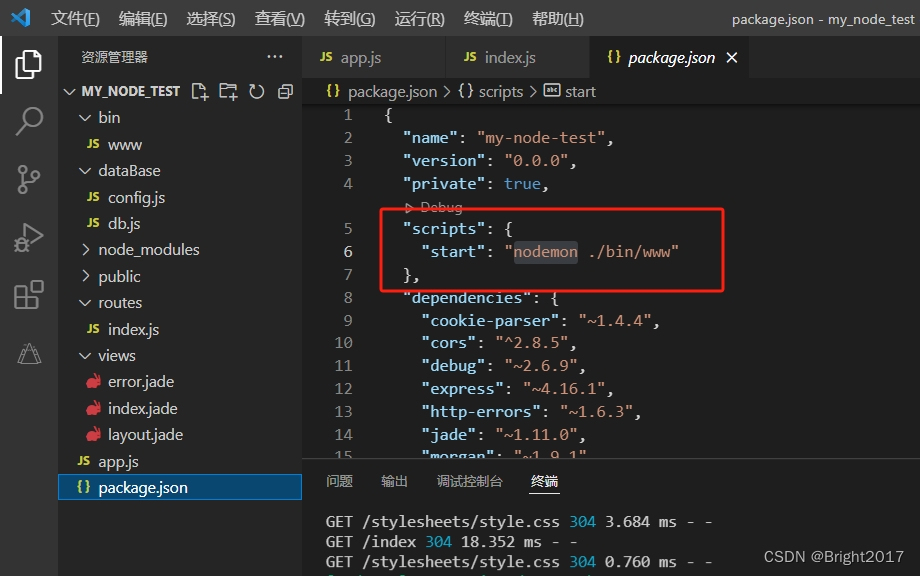
express-generator快速构建node后端项目
express-generator是express官方团队开发者准备的一个快速生成工具,可以非常快速的生成一个基于express开发的框架基础应用。 npm安装 npm install express-generator -g初始化应用 express my_node_test 创建了一个名为 my_node_test 的express骨架项目通过 Exp…...
视频监控系统/视频汇聚平台EasyCVR如何反向代理进行后端保活?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
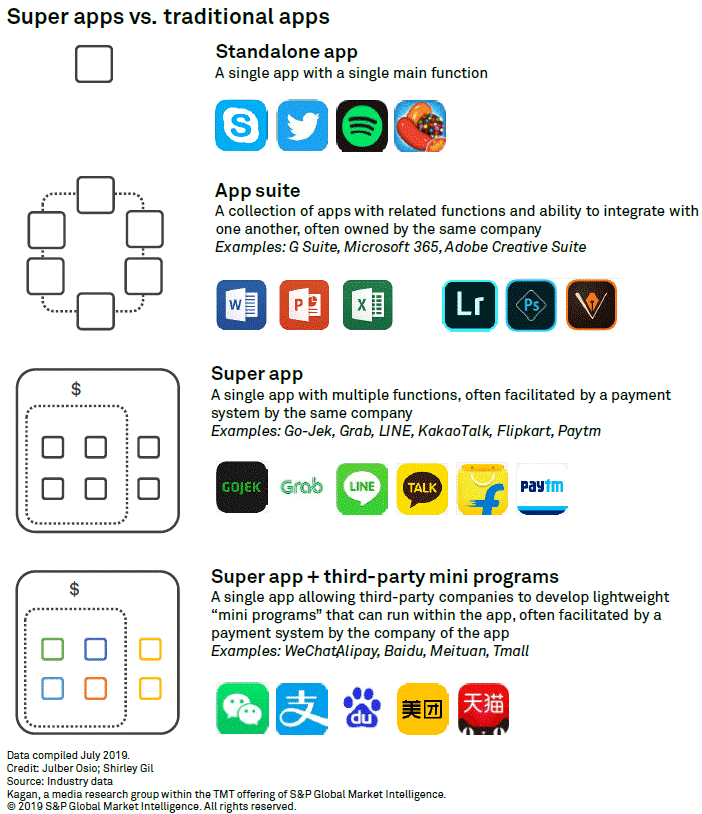
金融信创黄金三年:小程序生态+跨端技术框架构建
小程序应用场景生态的发展,受益于开源技术的发展,以及响应快速开发的实际业务需求,一些跨端框架如:Electron、wxPython、FinClip、Tauri、Flutter等发展也非常迅速,小程序生态跨端技术框架,不仅能满足自有超…...
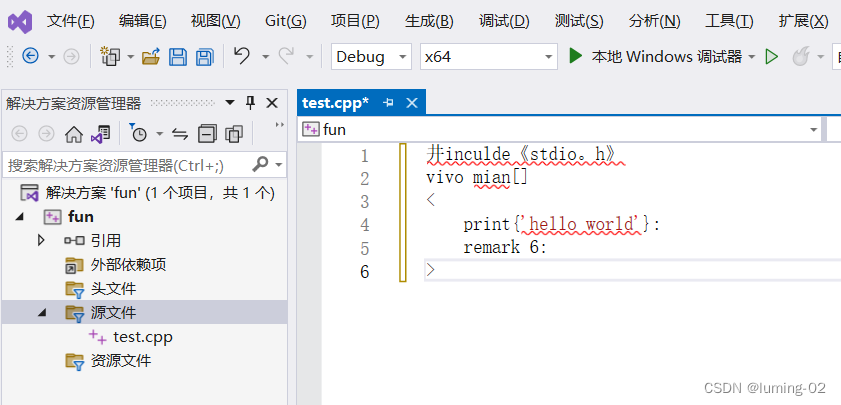
这短短 6 行代码你能数出几个bug?
前言:本文仅仅只是分享笔者一年前见到的诡异代码,大家可以看看乐子,随便数一数一共有多少个bug,这数bug多少还是要点水平的 在初学编程的时候,写的第一个代码大多都是 hello world,可是就算是 hello world…...

【毕设选题】深度学习 机器视觉 车位识别车道线检测 - python opencv
0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到毕业答辩的要求,这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师的要求。 为了大家能够顺利以及最少的精力通过…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
