【计算机物理模拟】-力矩、转动惯量和角速度之间的关系
力矩和角速度之间的关系可以通过牛顿第二定律和角动量定理来描述。
牛顿第二定律表明,物体的加速度与作用在物体上的合力成正比,加速度的方向与合力的方向相同。而对于旋转运动的物体,其加速度可以表示为半径 rrr 乘以角加速度 α\alphaα,即 a=rαa=r\alphaa=rα。因此,物体的转动加速度与作用在物体上的合力矩成正比。这个比例系数就是物体的转动惯量 III,即:
τ=Iα\tau=I\alphaτ=Iα
其中,τ\tauτ 表示作用在物体上的合力矩。
另一方面,角动量定理表明,物体的角动量守恒,当物体受到的合力矩为零时,其角动量保持不变。对于一个旋转运动的物体,其角动量 LLL 可以表示为转动惯量 III 乘以角速度 ω\omegaω,即:
L=IωL=I\omegaL=Iω
因此,可以得到力矩、转动惯量和角速度之间的关系:
τ=Iα=Idωdt=Id2θdt2=Id2dt2(rω)=Iddt(rα)=Iddt(rτI)=rτ\tau=I\alpha=I\frac{d\omega}{dt}=I\frac{d^2\theta}{dt^2}=I\frac{d^2}{dt^2}(r\omega)=I\frac{d}{dt}(r\alpha)=I\frac{d}{dt}(r\frac{\tau}{I})=r\tauτ=Iα=Idtdω=Idt2d2θ=Idt2d2(rω)=Idtd(rα)=Idtd(rIτ)=rτ
其中 θ\thetaθ 表示物体的角位移,rrr 表示物体围绕中心旋转的半径。因此,可以得到力矩 τ\tauτ、转动惯量 III 和角速度 ω\omegaω 之间的关系为 τ=rIα=rL\tau=rI\alpha=rLτ=rIα=rL。这个关系表明,当物体的转动惯量增大时,为了产生相同的角加速度,需要更大的力矩;当物体的角速度增大时,为了产生相同的力矩,需要更大的转动惯量
相关文章:

【计算机物理模拟】-力矩、转动惯量和角速度之间的关系
力矩和角速度之间的关系可以通过牛顿第二定律和角动量定理来描述。 牛顿第二定律表明,物体的加速度与作用在物体上的合力成正比,加速度的方向与合力的方向相同。而对于旋转运动的物体,其加速度可以表示为半径 rrr 乘以角加速度 α\alphaα&a…...

async和await用法理解和快速上手 , 同步任务和异步任务顺序安排和轻松理解 , js代码执行顺序表面知道
学习关键语句 : async , await 用法 await 怎么使用 同步任务和异步任务 微任务和宏任务 js中代码执行顺序 写在前面 虽然说 async 和 await 是 Promise 的语法糖 , 但是用惯了Promise 的人(我) , 还真不能超快速使用上这个语法糖 , 所以赶紧写一篇文章出来让各位了解了解这个…...
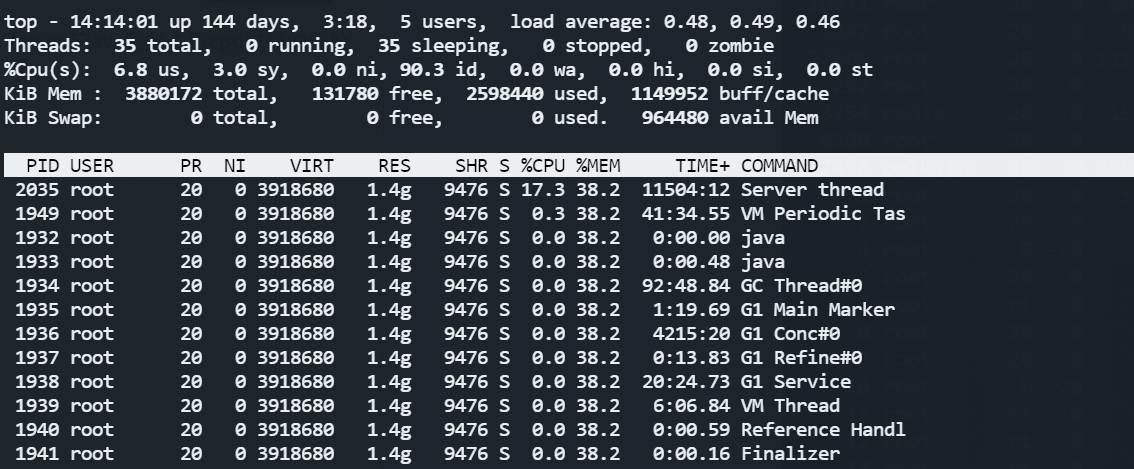
Linux下java服务占用cpu过高如何处理
Linux下java服务占用cpu过高如何处理 top命令查看进程信息 top按下shiftp,按cpu使用率排行,可见进程1932占用最高,并且是一个java服务 使用jps命令确认java服务 [rootVM-16-16-centos ~]# jps 1011 Jps 9462 yuan_back-0.0.1-SNAPSHOT.jar 1932 spigot-1.18.jar查找异常进程中…...
ros下用kinectv2运行orbslam2
目录 前提 创建工作空间 orbslam2源码配置、测试: 配置usb_cam ROS功能包 配置kinect 前提 vim 、 cmake 、 git 、 gcc 、 g 这些一般都装了 主要是Pangolin 、 OpenCV 、 Eigen的安装 18.04建议Pangolin0.5 创建工作空间 我们在主目录下创建一个catkin_…...

MVP简单模型搭建【架构】
MVP简介 MVP是一种项目架构设计模式(说白了就是我们产品的一种设计方案) 其实MVP本质 就是将View和Model完全隔离,通过Presenter统一调度管理(Presenter扮演着中介的角色)传统的设计思路是我们直接跟房东谈࿰…...
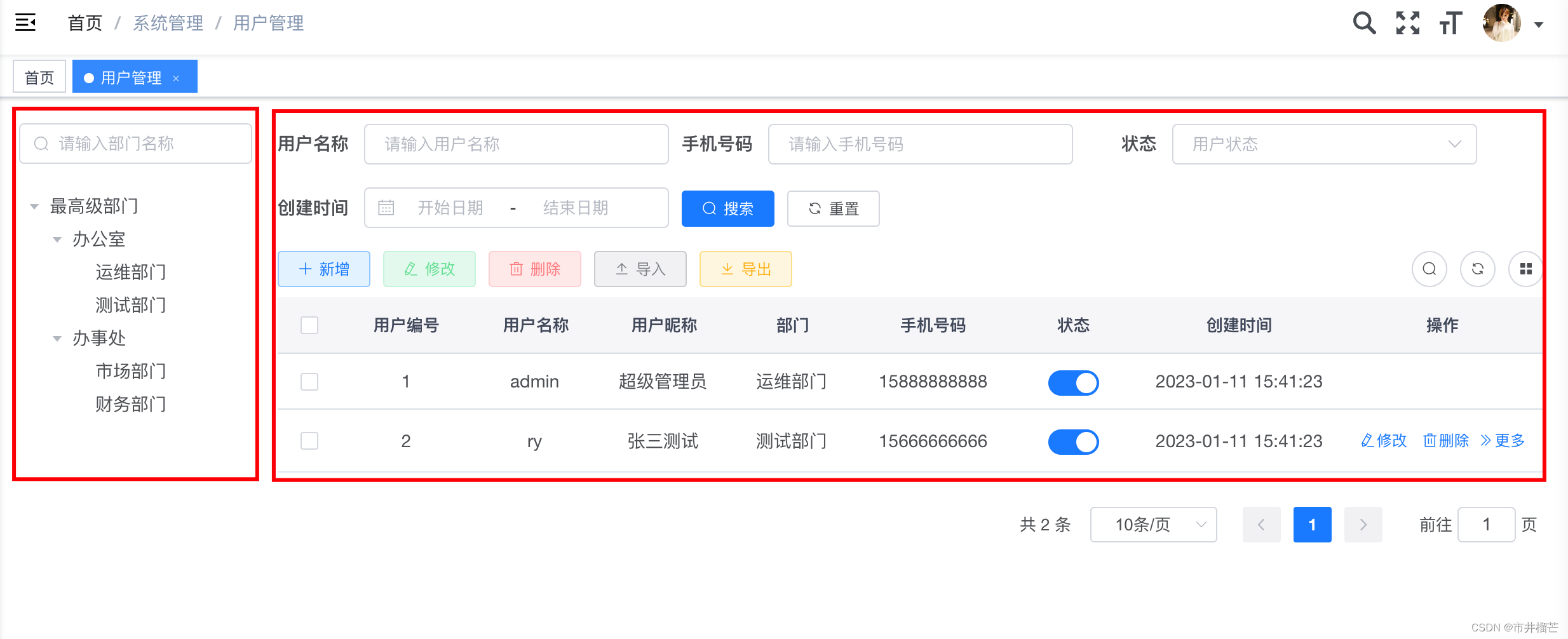
若依ruoyi框架实现目录树与查询页面联动
目录1、业务场景2、前端api.js修改index.vue修改template修改script修改3、后端controllerserviceimpldomainentitytreeselect1、业务场景 后管页面实现目录数与查询页面的联动,类似若依框架用户管理页面。 2、前端 api.js修改 在原有的js文件里配置目录树的查…...
Laravel框架学习笔记——Laravel环境配置及安装(Ubuntu20.04为例)
目录引言1、安装Nginx2、安装PHP3、安装Composer4、搭建Laravel框架项目5、修改Nginx映射6、安装MySQL引言 好久没写博客了,因为个人需要, 所以要涉及到Laravel框架的学习,所以会出一系列的关于PHP的Laravel框架学习笔记,希望能够…...
模拟百度翻译-课后程序(JAVA基础案例教程-黑马程序员编著-第六章-课后作业)
【案例6-5】 模拟百度翻译 【案例介绍】 1.任务描述 大家对百度翻译并不陌生,本案例要求编写一个程序模拟百度翻译。用户输入英文之后搜索程序中对应的中文,如果搜索到对应的中文就输出搜索结果,反之给出提示。本案例要求使用Map集合实现英…...
自然语言处理(NLP)之求近义词和类比词<MXNet中GloVe和FastText的模型使用>
这节主要就是熟悉MXNet框架中的两种模型:GloVe和FastText的模型(词嵌入名称),每个模型下面有很多不同的词向量,这些基本都来自wiki维基百科和twitter推特这些子集预训练得到的。我们只需要导入mxnet.contrib中的text模块即可,这里…...
)
2023年CDGA考试-第13章-数据质量(含答案)
2023年CDGA考试-第13章-数据质量(含答案) 单选题 1.在导致数据质量问题的常见原因中关于数据输入问题以下描述正确的是: A.数据采集端缺乏数据质量管控 B.相同字段重复设计导致数据不一致 C.缺乏数据采集规范的制定 D.所有描述都正确 答案 D 2.数据质量计划应将其范围限…...
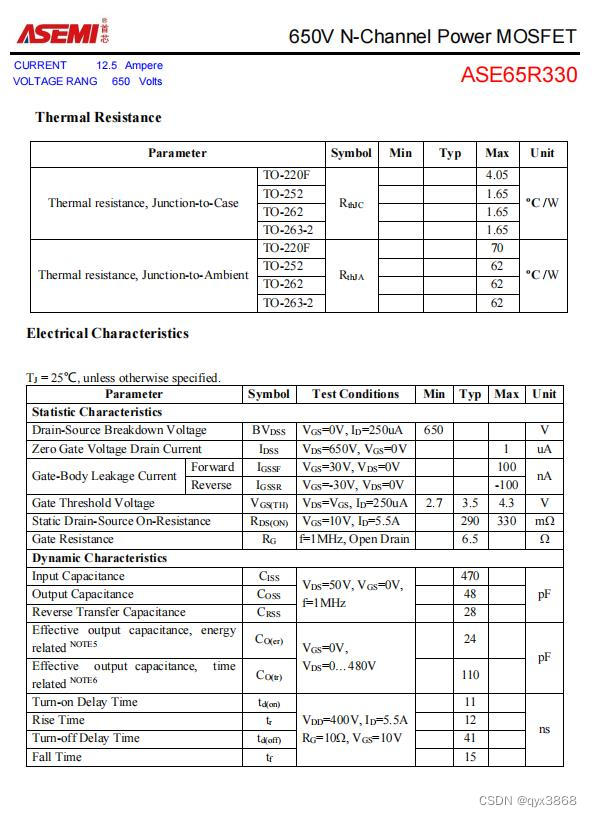
ASEMI高压MOS管ASE65R330参数,ASE65R330图片
编辑-Z ASEMI高压MOS管ASE65R330参数: 型号:ASE65R330 漏极-源极电压(VDS):650V 栅源电压(VGS):20V 漏极电流(ID):12.5A 功耗(P…...
:子序列、子数组问题)
LeetCode动态规划经典题目(九):子序列、子数组问题
目录 31. LeetCode674. 最长连续递增序列 32. LeetCode18. 最长重复子数组 33. LeetCode1143. 最长公共子序列 34. LeetCode1035. 不相交的线 35. LeetCode53. 最大子数组和 36. LeetCode392.判断子序列 37. LeetCode115. 不同的子序列 38. LeetCode583. 两个字符串的删…...

如何利用有限的数据发表更多的SCI论文?——利用ArcGIS探究环境和生态因子对水体、土壤和大气污染物的影响
SCI的写作和发表是科研人提升自身实力和实现自己价值的必要途径。“如何利用有限的数据发表更多的SCI论文?”是我们需要解决的关键问题。软件应用只是过程和手段,理解事件之间的内在逻辑和寻找事物之间的内在规律才是目的。如何利用有限的数据发表更多的…...
六【 SpringMVC框架】
一 SpringMVC框架 目录一 SpringMVC框架1.什么是MVC2.SpringMVC概述3.SpringMVC常见开发方式4.SpringMVC执行流程5.SpringMVC核心组件介绍6.快速构建Spring MVC程序✅作者简介:Java-小白后端开发者 🥭公认外号:球场上的黑曼巴 🍎个…...
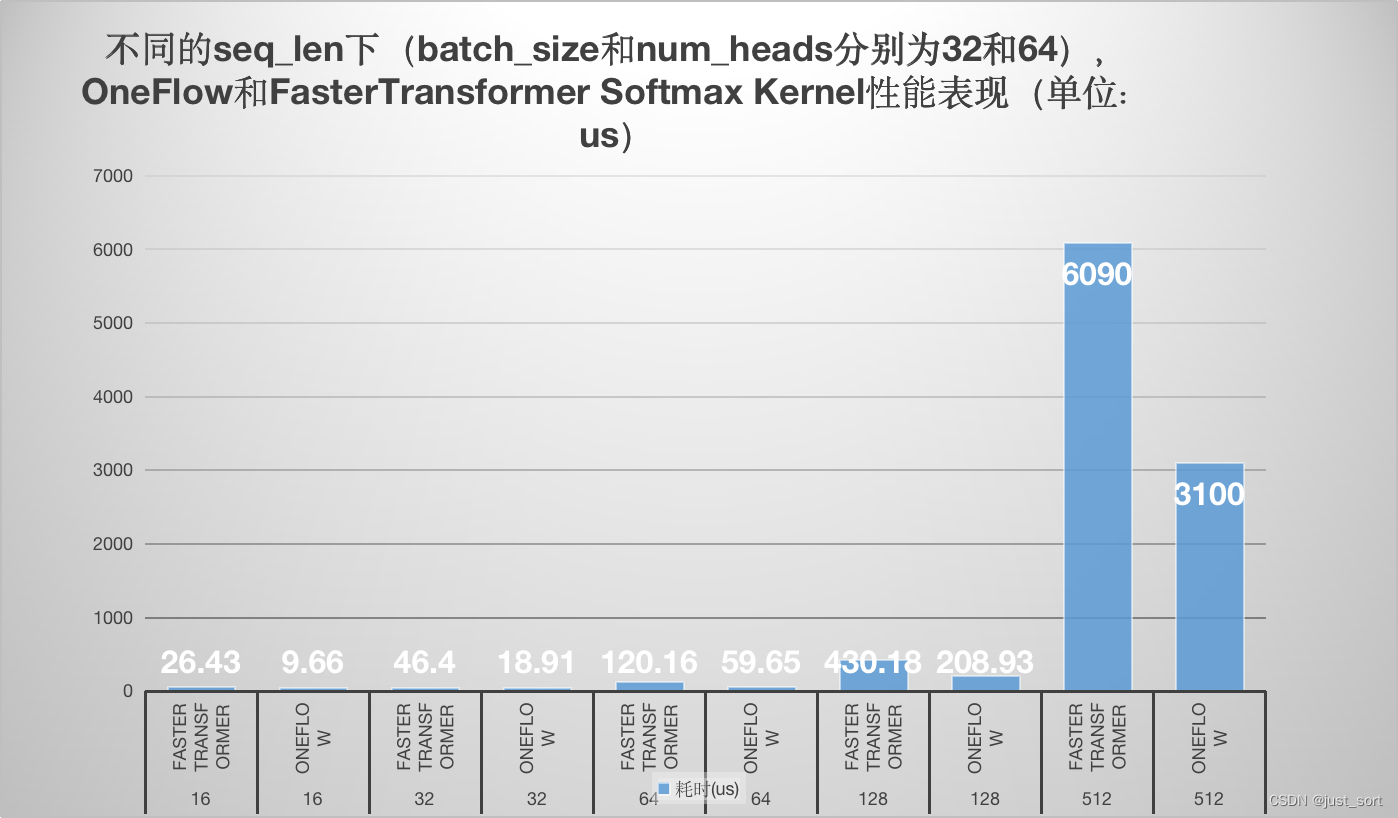
【BBuf的CUDA笔记】八,对比学习OneFlow 和 FasterTransformer 的 Softmax Cuda实现
0x1. OneFlow/FasterTransformer SoftMax CUDA Kernel 实现学习 这篇文章主要学习了oneflow的softmax kernel实现以及Faster Transformer softmax kernel的实现,并以个人的角度分别解析了原理和代码实现,最后对性能做一个对比方便大家直观的感受到onefl…...

python 类对象的析构释放代码演示
文章目录一、类的构造函数与析构函数二、代码演示1. 引用的更迭2. 只在函数内部的类对象三、函数内部返回的类对象1. 使用全局变量 引用 函数内部的类对象一、类的构造函数与析构函数 init 函数是python 类的构造函数,在创建一个类对象的时候,就会自动调…...
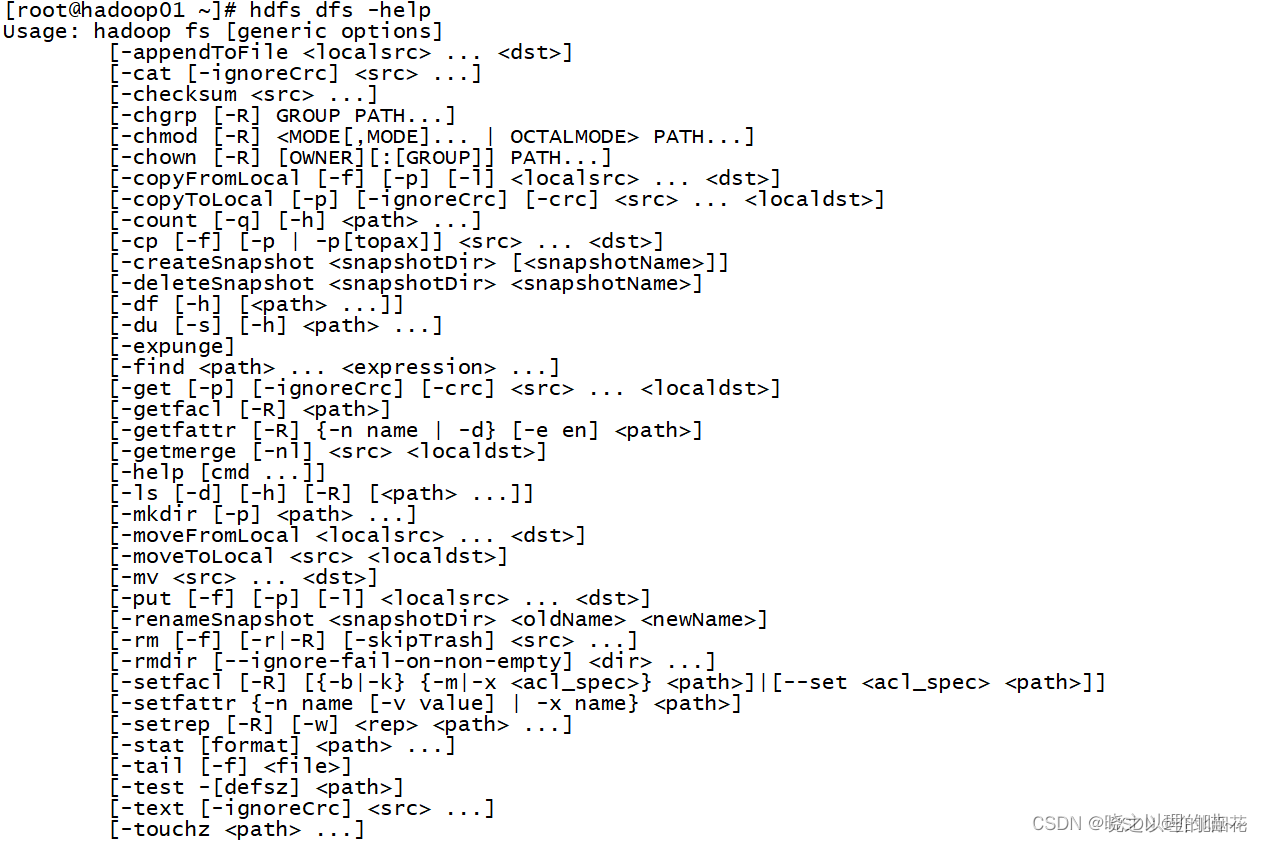
Hadoop Shell常用命令
Hadoop Shell命令在管理HDFS的时候还是比较常用的,Hadoop Shell命令与shell命令极为相似,但是方便查询,在这里总结分享,大家enjoy~~ 1,cat 语法格式:hadoop fs -cat URI [URI …] 含义:将路径…...

Android中级——色彩处理和图像处理
色彩处理 通过色彩矩阵处理 色彩矩阵介绍 图像的RGBA可拆分为一个4行5列的矩阵和5行1列矩阵相乘 其中4行5列矩阵即为ColorMatrix,可通过调整ColorMatrix间接调整RGBA 第一行 abcde 决定新的 R第二行 fghij 决定新的 G第三行 klmno 决定新的 G第四行 pqrst 决定新…...
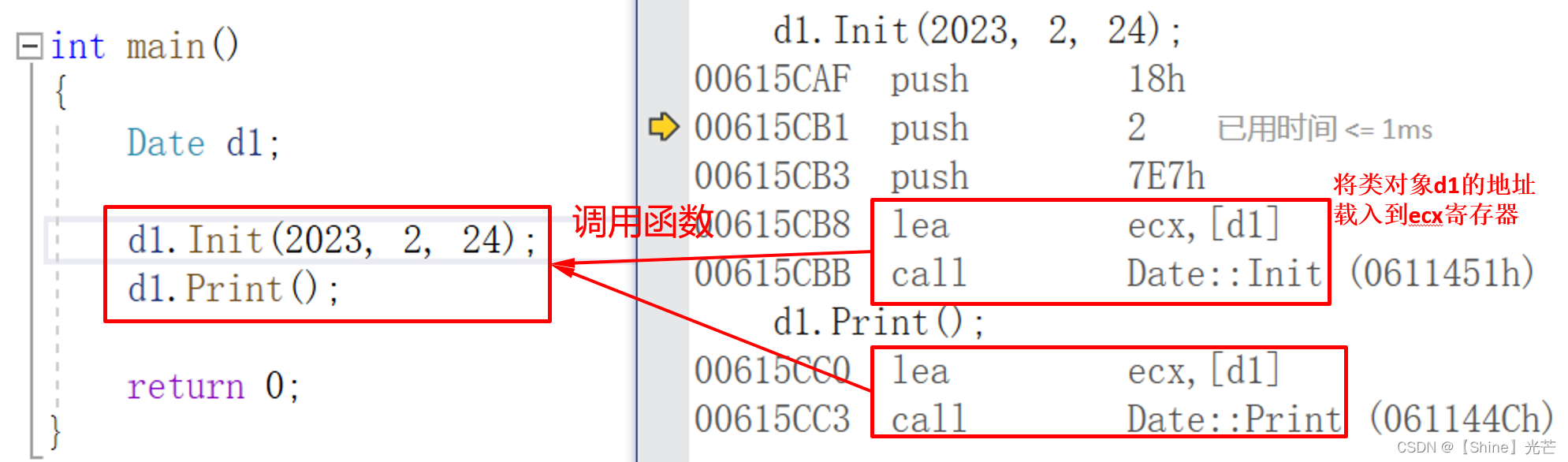
C++类和对象:类的定义、类对象的存储、this指针
目录 一. 对于面向过程和面向对象的认识 二. 类 2.1 struct关键字定义类 2.1.1 C语言中的struct关键字 2.1.2 C中的struct关键字 2.2 class关键字 2.1 使用class关键字定义类 三. 类的访问限定及封装 3.1 类的访问权限及访问限定符 3.1.1 访问权限 3.1.2 访问限定…...
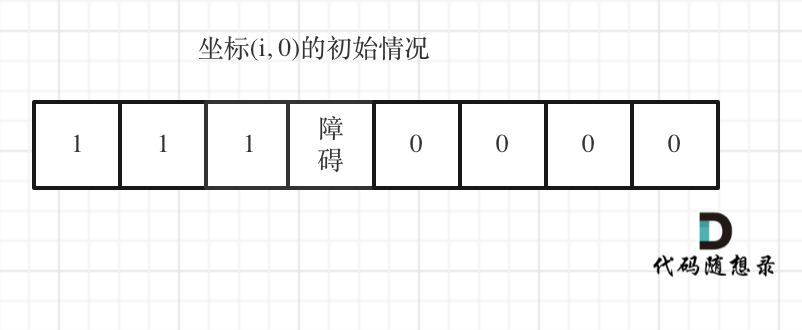
代码随想录算法训练营第三十九天 | 62.不同路径,63. 不同路径 II
一、参考资料不同路径https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html 视频讲解:https://www.bilibili.com/video/BV1ve4y1x7Eu不同路径 IIhttps://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84II.htmlhttps://progr…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
