网站上线如何检查?
网站上线如何检查?很多企业搭建好网站之后,不知道如何检查网站,其实网站上线之后,要对网站的代码,网站的SEO细节,等重要因素检查,下面我们就来讲述一下企业优化网站建站、上线检查要求。
网站上线如何检查?企业优化网站建站、上线检查要求
1、企业简介,企业简介用封面页的形式
2、头部代码规范
3、各类小图片尽量用css调用
4、源代码用绝对路径(相对路径会有一个解析的过程)
5、css等文件不允许出现远程路径
6、网站首页、栏目页、内容页三层结构,不要www.xxx.com/cs/zl/bd/1.html这种多层的目录结构
7、最新文章模块后面加上时间调用(年/月/日)
8、QQ直接链接QQ对话,点击过去要可以直接对话,不要出现先添加好友的步骤
9、网站要添加cnzz统计代码,除了百度适配的js代码,其他诸如百度统计、百度网盟等产品js代码不要加。
10、注意检查浏览器兼容问题(IE6,7,8、谷歌、火狐)
11、首页TDK写死, 不要调用(title/keywords/description),栏目和文章页调用品牌词
12、首页第一屏的图片要注意有400电话/优化QQ的展示,logo没有,banner图片就要注意添加
13、文章页的文章标题用h1
14、死链接(包括图片、链接、css)要完全清除
15、用完整域名比用"/"好;栏目路径需带“/”的完整路径(/bdtf/)
16、编辑开始填充文章后不能随便更改栏目和覆盖后台数据
17、网站图片大小的统一性规范(手机站除头图30KB左右,其他图片尽量最小化,任何岗位上传到网站上面的每张图片都要出来后再上线,保证体积最小化)
18、代码能封装的要全部封装,不要放在网站的源码中,尤其首页js不超过4次;
检查完善后由对接人将网站交接给优化负责人检查网站错误、安排写关键词描述等。(如果是数据包网站,交接前需要删除原数据文章),程序员跟踪网站关键词描述完成情况,及时取消robots.txt屏蔽上线网站,取消robots屏蔽需告知对接人,手机网站的兼容性检查。(检查不同手机和浏览器和手机屏大小的兼容性,特别手机站的UC和iPhone自带浏览器兼容性);
相关文章:

网站上线如何检查?
网站上线如何检查?很多企业搭建好网站之后,不知道如何检查网站,其实网站上线之后,要对网站的代码,网站的SEO细节,等重要因素检查,下面我们就来讲述一下企业优化网站建站、上线检查要求。 网站上线如何检查…...
”?)
如何理解pytorch中的“with torch.no_grad()”?
torch.no_grad()方法就像一个循环,其中循环中的每个张量都将requires_grad设置为False。这意味着,当前与当前计算图相连的具有梯度的张量现在与当前图分离了我们将不再能够计算关于该张量的梯度。直到张量在循环内,它才与当前图分离。一旦用梯…...

Linux虚拟机克隆之后使用ip addr无法获取ip地址
Linux虚拟机克隆之后使用ip addr无法获取ip地址 因为克隆得到的虚拟机,与原先的linux系统是一模一样的包括MAC地址和IP地址。需要修改信息。 设置IP地址: 使用vi命令打开linux的网卡 //ifcfg-enth0是虚拟网卡的名称,如果你的不叫这个名字&a…...

日报系统:优化能源行业管理与决策的利器
日报系统:优化能源行业管理与决策的利器 引言: 随着能源行业的快速发展和复杂性增加,管理各个部门的数据变得至关重要。为了提高运营效率和决策的准确性,能源行业普遍采用日报系统作为综合数据汇报和分析的工具。本文将探讨日报系…...

linux安装idea
下载好之后是.tar.gz文件后缀的 使用命令解压安装包 tar -zxvf 你的安装包 解压好了之后进入解压好的目录找到bin文件里的idea.sh,使用命令启动它 ./idea.sh 这样你就可以在manjaro上使用idea了 在这里插入图片描述 需要手动创建快捷启动方式 每次都使用命令行启动是比较…...
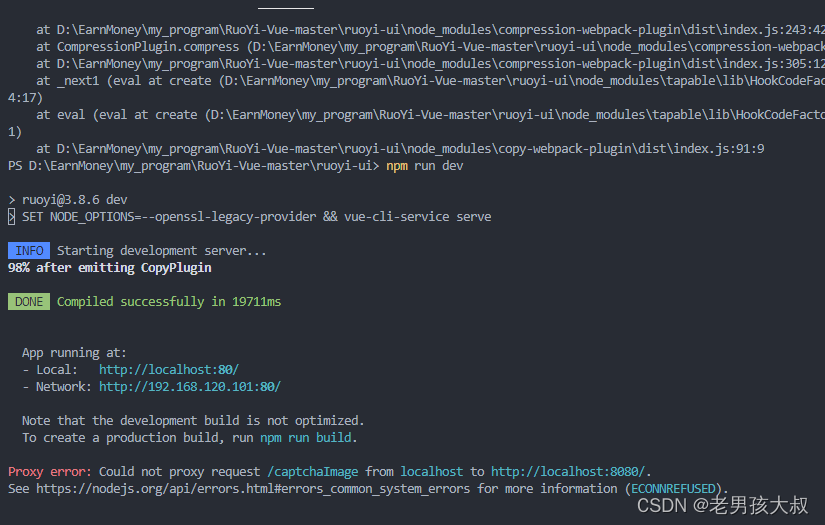
vue启动项目,npm run dev出现error:0308010C:digital envelope routines::unsupported
运行vue项目,npm run dev的时候出现不支持错误error:0308010C:digital envelope routines::unsupported。 在网上找了很多,大部分都是因为版本问题,修改环境之类的,原因是对的但是大多还是没能解决。经过摸索终于解决了。 方法如…...
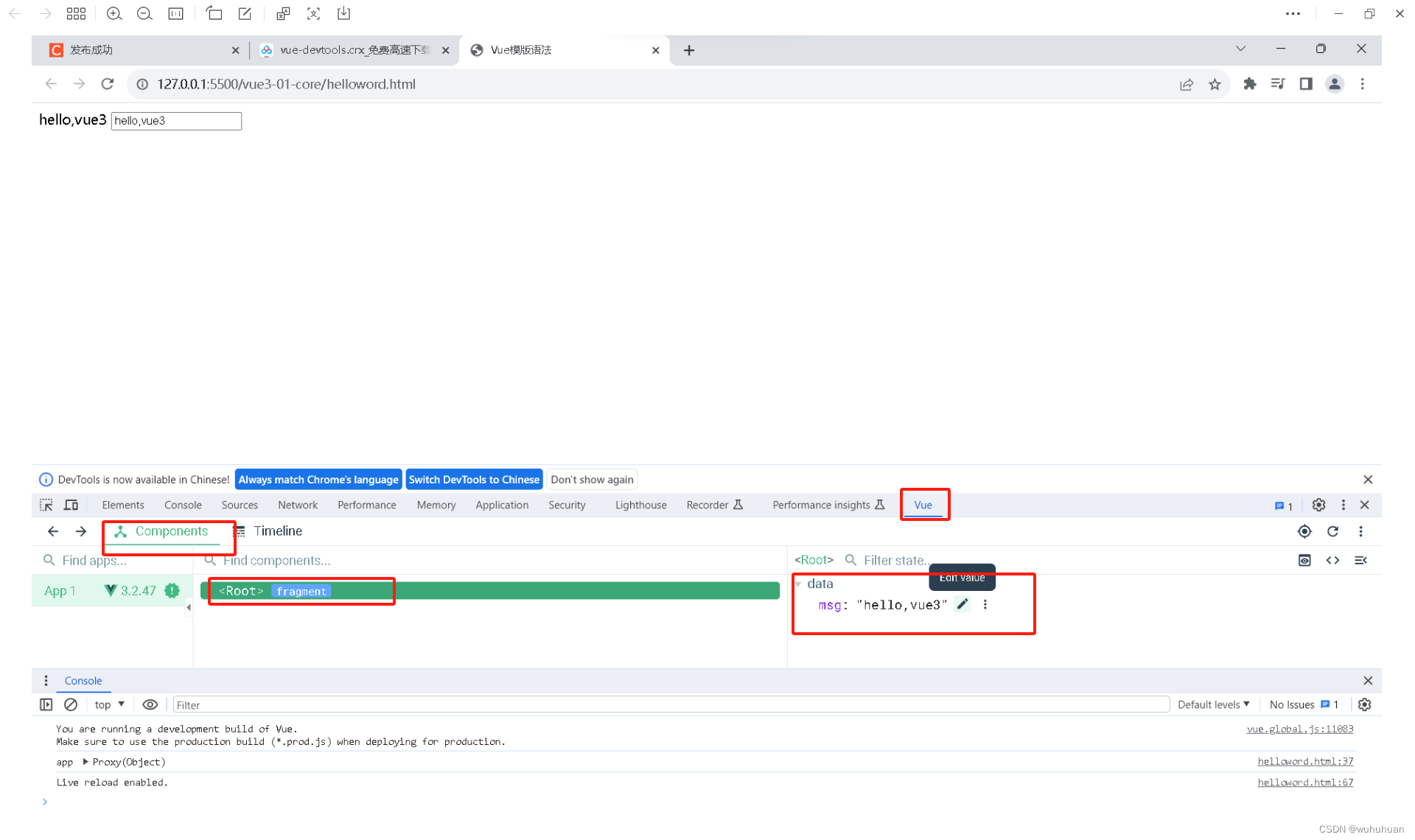
vue-devtools插件安装
拓展程序连接 链接:https://pan.baidu.com/s/1tEyZJUCEK_PHPGhU_cu_MQ?pwdr2cj 提取码:r2cj 一、打开谷歌浏览器,点击扩展程序-管理扩展程序 二、打开开发者模式,将vue-devtools.crx 拖入页面,点击添加扩展程序 成…...

const关键字
目录 修饰指针 指向常量的指针*ptr 指针常量:数据类型 * const 指针变量 修饰引用 const &...

HTML5+CSS3+JS小实例:仿优酷视频轮播图
实例:仿优酷视频轮播图 技术栈:HTML+CSS+JS 效果: 源码: 【html】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name="viewport" content=&quo…...

dart的Websocket为什么找不到onOpen方法?
我主要使用的是JAVA,而JAVA使用Websocket时,Websocket一定会有个onOpen方法。 ClientEndpoint public class WebsocketListener {OnOpenpublic void onOpen(Session session) throws IOException {}OnMessagepublic void onMessage(ByteBuffer byteBuff…...
无法连接网络解决办法记录)
VMware中Ubuntu(Linux)无法连接网络解决办法记录
问题: 操作系统:Ubuntu 22.04.3 LTS VMware 版本:VMware Workstation 17 Pro, 17.0.0 build-20800274今天在虚拟机用Ubuntu的时候,发现无法连接网络,如下: wdwd-virtual-machine:~$ ifconfig lo: flags73…...

js结合map对象等处理数组
cpp const INVENTORY_STATUS_MAP {7: { text: 全部 },0: { text: 出租, color: mary-green },1: { text: 已售, color: mary-green },2: { text: 丢失, color: mary-orange },3: { text: 闲置, color: mary-green },4: { text: 退役, color: mary-orange },5: { text: 售后, c…...

网络攻防实战演练
在经历了多年的攻防对抗之后,大量目标单位逐渐认识到安全防护的重要性。因此,他们已采取措施尽可能收敛资产暴露面,并加倍部署各种安全设备。但安全防护注重全面性,具有明显的短板... 1、供应链 在经历了多年的攻防对抗之后&…...

基于Keil a51汇编 —— 标准宏定义
定义标准宏 标准宏定义如下: macro-name MACRO <[>parameter-list<]> <[>LOCAL local-labels<]> . . . macro-body . . .ENDMmacro-name 宏的名称 parameter-list 可以传递给宏的形式参数的可选列表 LOAD_R0 MACRO R0_ValMOV R0, #R0_…...

遍历List集合
1.初始化 // 写法一 List<String> list new ArrayList<>(); list.add("a"); list.add("b"); list.add("c");// 写法二 List<String> list new ArrayList(){{add("a");add(&quo…...
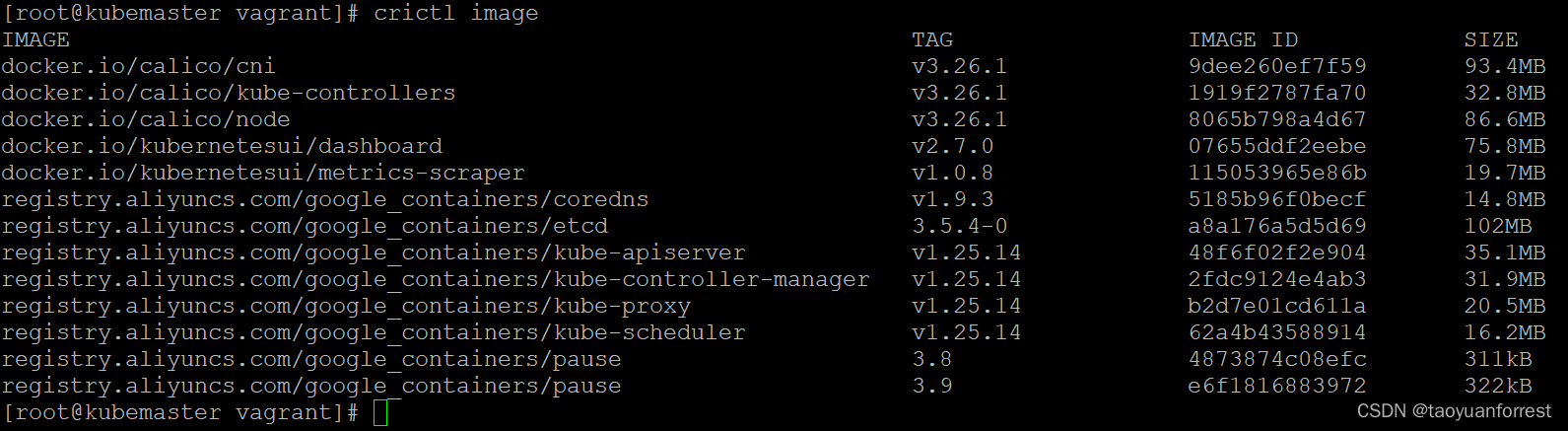
k8s containerd查看镜像
直接查看crictl image会报错: 1) crictl config runtime-endpoint unix:///run/containerd/containerd.sock 2) vi /etc/crictl.yaml 3) systemctl daemon-reload 此时,再查看image:...
)
acwing.893. 集合-Nim游戏(博弈论sg函数模板)
给定 n� 堆石子以及一个由 k� 个不同正整数构成的数字集合 S�。 现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 S�,最后无法进行操作的人视…...

数据安全防护:云访问安全代理(CASB)
云访问安全代理(Cloud Access Security Broker,CASB),是一款面向应用的数据防护服务,基于免应用开发改造的配置方式,提供数据加密、数据脱敏功能。数据加密支持国密算法,提供面向服务侧的字段级…...

面试准备-操作系统
参考: 《程序员面试笔试宝典》(何昊、叶向阳) 进程是系统进行资源分配和调度的一个独立单位。线程是进程的一个实体,是cpu调度和分配的基本单位。线程基本不拥有系统资源,只拥有必须的,但是同属于一个进程…...

深度学习基础知识 Batch Normalization的用法解析
深度学习基础知识 Batch Normalization的用法解析 import numpy as np import torch.nn as nn import torchdef bn_process(feature, mean, var):feature_shape feature.shapefor i in range(feature_shape[1]):# [batch, channel, height, width]feature_t feature[:, i, :,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
