【Codeforces】Educational Codeforces Round 156 [Rated for Div. 2]
hh第一次记录cf。
复盘
ab题目比较清晰,只开了这两题,后面看了下cd,即使开了翻译也看不懂题目是什么意思,最后放弃睡觉了。。
a是一道思维题,翻了下别人写的发现大家写的各不相同hh
b是一道数学题,过程有点繁琐,需要细心。

Problem - A - Codeforces
数学巧思
题意:
仍然是t组测试哈,给定一个数n,问是否有a+b+c=n,a%3,b%3,c%3不为0,如果存在输出yes并输出这三个数,否则输出no。
设a=3k1+d1,b=3k2+d2,c=3k3+d3
显然,d1,d2,d3只能是1或2
那么我们就只需要对余数进行讨论就行了,
比如给定1和2,这两个数当然是满足条件的,只需要(n-3)%3不为0就好了,也就是(n-3)=3*k+1或2(k>=1)
这一个条件不足以涵盖所有情况,也就是只要还需要n-(3*k+1),n-(3*k+2),即覆盖余数为0,1,2这三种情况
#include<bits/stdc++.h>
signed main()
{int t;std::cin>>t;while(t--){int x;std::cin>>x;if((x-3)%3&&(x-3)!=1&&(x-3)!=2&&(x-3)>0){std::cout<<"YES"<<'\n'<<"1 2 "<<x-3<<'\n';continue;}if((x-5)%3&&(x-5)!=1&&(x-5)!=4&&(x-5)>0){std::cout<<"YES"<<'\n'<<"1 4 "<<x-5<<'\n';continue;}if((x-7)%3&&(x-7)!=2&&(x-7)!=5&&(x-7)>0){std::cout<<"YES"<<'\n'<<"2 5 "<<x-7<<'\n';continue;}std::cout<<"NO"<<'\n';}return 0;
}但其实经过分析可以发现,只需要上面两个if语句就够了,n-3和n-5已经覆盖了所有情况。
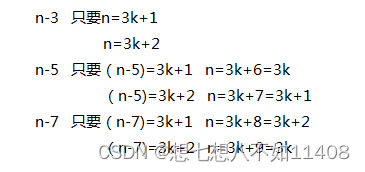
常规循环
因为思路比较简单我就直接复制的别人的代码,枚举前两个数,范围是1-13,然后对n-i-j进行判断就行。
#define ll long long
#include<bits/stdc++.h>
using namespace std;void solve(){ll n;cin>>n;for(ll i=1;i<13;i++){for(ll j=1;j<13;j++){ll z=n-i-j;if(z>0 && i!=j && i!=z && j!=z && i%3!=0 && j%3!=0 && z%3!=0){cout<<"Yes"<<"\n";cout<<i<<" "<<j<<" "<<z<<"\n";return;}}}cout<<"No"<<"\n";
}int main(){ll n;cin>>n;while(n--)solve();
}Problem - B - Codeforces
题目仍然是t个测试点
题目给出三个点p,a,b,要求以a和b分别为圆心,以w为半径做两个圆
要求o到p在圆上有路
思路分析:
#include<bits/stdc++.h>
using namespace std;
int dis(int x1,int y1,int x2,int y2)
{return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
signed main()
{int t;std::cin>>t;while(t--){int p1,p2;int x1,y1;int x2,y2;std::cin>>p1>>p2>>x1>>y1>>x2>>y2;//只要源点和p都在圆上 //double s1=min(max(dis(p1,p2,x1,y1),dis(0,0,x1,y1)),max(dis(p1,p2,x2,y2),dis(0,0,x2,y2)));double hh=(double)dis(x1,y1,x2,y2)/4;double s2=max(hh,(double)min(max(dis(p1,p2,x1,y1),dis(0,0,x2,y2) ),max(dis(p1,p2,x2,y2),dis(0,0,x1,y1))));double d=min(s1,s2);d=sqrt(d);printf("%.10f\n",d);}return 0;
}
相关文章:
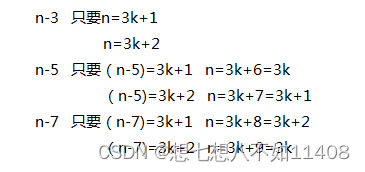
【Codeforces】Educational Codeforces Round 156 [Rated for Div. 2]
hh第一次记录cf。 复盘 ab题目比较清晰,只开了这两题,后面看了下cd,即使开了翻译也看不懂题目是什么意思,最后放弃睡觉了。。 a是一道思维题,翻了下别人写的发现大家写的各不相同hh b是一道数学题,过程有点…...

结合swagger的前端架构小记
1.引言 开发中,我们是否经常遇到以下痛点: 项目越大,启动和热更新越来越慢,启动都要花个3-5分钟以上没有类型,接口返回的Object不拿到真实数据都不知道有哪些字段需要手动写很多request函数去调用api,手动…...

Python字典全解析:从基础到高级应用
更多资料获取 📚 个人网站:涛哥聊Python 字典是一种强大而多才多艺的数据类型,它以键-值对的形式储存信息,让我们能够以惊人的效率处理和管理数据。 字典能够将键和值关联在一起,使得数据的存储和检索变得非常高效。…...

Fourier变换中的能量积分及其详细证明过程
Fourier变换中的能量积分及其详细证明过程 在使用Fourier变换分析信号时候,有时需要用到能量积分。本文对Fourier变换的能量积分进行分析。 一、Fourier变换中的能量积分 若 F ( ω ) F [ f ( t ) ] F(\omega)\mathscr F[f(t)] F(ω)F[f(t)],则有 ∫…...

保护 Web 服务器安全性
面向公众的系统(如 Web 服务器)经常成为攻击者的目标,如果这些业务关键资源没有得到适当的保护,可能会导致安全攻击,从而导致巨大的财务后果,并在客户中失去良好的声誉。 什么是网络服务器审核 当有人想要…...

docker数据管理和网络通信
docker数据管理 管理 Docker 容器中数据主要有两种方式: 数据卷(Data Volumes)和数据卷容器(DataVolumes Containers)。 1.数据卷 数据卷是一个供容器使用的特殊目录,位于容器中。可将宿主机…...

代理IP与Socks5代理:网络工程师的神奇魔法棒
网络工程师是数字世界的魔法师,而代理IP和Socks5代理则是他们的神奇魔法棒。这两项技术在跨界电商、爬虫、出海业务、网络安全和游戏等领域中,为网络工程师提供了强大的工具,让他们能够创造技术的奇迹。本文将深入研究这些神奇魔法棒在不同领…...

【K8S系列】深入解析k8s 网络插件—kube-router
序言 做一件事并不难,难的是在于坚持。坚持一下也不难,难的是坚持到底。 文章标记颜色说明: 黄色:重要标题红色:用来标记结论绿色:用来标记论点蓝色:用来标记论点 在现代容器化应用程序的世界中…...

Flutter的Platform介绍-跨平台开发,如何根据不同平台创建不同UI和行为
文章目录 Flutter跨平台概念介绍跨平台开发平台相关性Platform ChannelPlatform-specific UIPlatform Widgets 如何判断当前是什么平台实例 Platform 类介绍获取当前平台的名称检查当前平台其他属性 利用flutter设计跨Android和IOS平台应用的技巧1. 遵循平台的设计准则2. 使用平…...

gitlab docker部署,备份,恢复
本次安装在CentOS7下进行 1、安装yum 检查是否已经安装yum yum --version如果未安装 sudo yum install -y yum-utils添加镜像源: 国外镜像源:yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo阿里镜像源&am…...

腾讯云/阿里云国际站代理:阿里云、华为云和腾讯云“大展拳脚”,与国际巨头未来竞争焦点是AI计算?
国内云计算市场重新掀起的价格战,腾讯云国际站代理让竞争本就内卷的市场陷入白热化,中国云厂商深耕东南亚的意愿变强。2020年之后,上下游企业与中国云厂商抱团出海趋势明显。东软集团、用友网络等A股上市公司也在走向东南亚。 东南亚市场蛋糕…...
基于Java+SpringBoot+Vue企业OA管理系统的设计与实现 前后端分离【Java毕业设计·文档报告·代码讲解·安装调试】
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

Java架构师系统架构设计性能评估
目录 1 导论2 架构评估基础系统性能衡量的基本指标2.1 系统性能的指标2.2 数据库指标2.3 并发用户数2.4 网络延迟2.4 系统吞吐量2.5 资源性能指标3 架构评估基础服务端性能测试3.1基准测试3.2 负载测试3.3 压力测试3.4 疲劳强度测试3.5 容量测试1 导论 本章的主要内容是掌握架构…...

Android可滑动的分时图以及常用动画
先看一下效果: 自定义View 其中顶部是模仿的股票数据分时图,以前也写过详细的文章传送门,只不过不支持左右滑动,这款是在那个基础上的修改 在说一下分时图的思路吧: 可以看作是一条条相连的直线首尾相接,…...
)
软考系统架构师常考知识点整理(含案例分析、论文历年题目总结)
系统架构师常考知识点总结 计算机组成原理 1、同步/异步区分 CPU访问内存通常是同步方式 CPU与I/O接口交换信息通常是同步方式 CPU与PCI总线交换信息通常是同步方式 I/O接口与打印机交换信息则通常采用基于缓存池的异步方式, 2、双工通信方式 对端到端通信总线的信号传…...
Netty通信在中间件组件中的广泛使用-Dubbo3举例
Netty是一个高性能异步IO通信框架,封装了NIO,对各种bug做了很好的优化解决。所以很多中间件底层的通信都会使用Netty,比如说:Dubbo3,rocketmq,ElasticSearch等。 比方说,我们使用dubbo作为rpc跨…...
基于Java的在线拍卖系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技…...

Maven Pom
目录 Pom 父(Super)POM POM 标签大全详解 POM( Project Object Model,项目对象模型 ) 是 Maven 工程的基本工作单元,是一个XML文件,包含了项目的基本信息,用于描述项目如何构建,声明项目依赖…...

【运维日常】mongodb 集群生产实践
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...
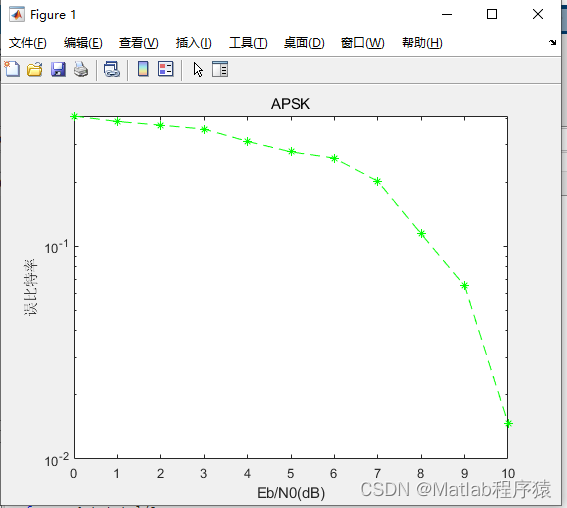
【MATLAB源码-第45期】基于matlab的16APSK调制解调仿真,使用卷积编码软判决。
操作环境: MATLAB 2022a 1、算法描述 1. 16APSK调制解调 16APSK (16-ary Amplitude Phase Shift Keying) 是一种相位调制技术,其基本思想是在恒定幅度的条件下,改变信号的相位,从而传送信息。 - 调制:在16APSK中&am…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...
