【Codeforces】 CF1762E Tree Sum
题目链接
CF方向
Luogu方向
题目解法
首先考虑 n n n 为奇数的情况无解,这个可以通过乘积矛盾简单证明
接下来考虑一个结论是:偶数个点的树的形态确定之后,只有恰好 1 1 1 种染色方案,即从叶子一层一层往上面染,这样一定可以构造出来解且唯一
考虑一个更强的结论是:一条边的边权为 1 1 1 当且仅当这条边对应的两个子树大小都为偶数
为什么?考虑 s i z siz siz 为奇数的情况一定不可能点全部合法,但又要使它合法,只能让子树根的乘积为 1 1 1,然后令上面连向整体的边为 − 1 -1 −1 即可
s i z siz siz 全为偶数的情况用反证法不难证出
现在有一个很重要的 t r i c k trick trick(我也要提醒我自己!!!)是:对于每条边考虑它的贡献,然后类和
这样就好算了,对于一条连接大小为 i , n − i i,n-i i,n−i 的子树的边(必须在 1 − n 1-n 1−n 路径上),贡献为 ( n − 2 i − 1 ) f i f n − i i ( n − i ) \binom{n-2}{i-1}f_if_{n-i}i(n-i) (i−1n−2)fifn−ii(n−i)
其中 f i f_i fi 为 i i i 个点的树的形态方案数,即为 i i − 2 i^{i-2} ii−2
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
using namespace std;
const int N=500100,P=998244353;
int n,fac[N],inv[N],f[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int qmi(int a,int b){int res=1;for(;b;b>>=1){if(b&1) res=1ll*res*a%P;a=1ll*a*a%P;}return res;
}
int C(int a,int b){if(a<b||b<0) return 0;return 1ll*fac[a]*inv[b]%P*inv[a-b]%P;
}
int main(){n=read();if(n&1){ puts("0");exit(0);}fac[0]=1;for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%P;inv[n]=qmi(fac[n],P-2);for(int i=n-1;i>=0;i--) inv[i]=1ll*inv[i+1]*(i+1)%P;f[1]=1;for(int i=2;i<=n;i++) f[i]=qmi(i,i-2);int ans=0;for(int i=1,neg=-1;i<n;i++,neg*=-1) ans=(ans+1ll*neg*C(n-2,i-1)*f[i]%P*f[n-i]%P*i%P*(n-i))%P;printf("%d\n",(ans+P)%P);return 0;
}相关文章:

【Codeforces】 CF1762E Tree Sum
题目链接 CF方向 Luogu方向 题目解法 首先考虑 n n n 为奇数的情况无解,这个可以通过乘积矛盾简单证明 接下来考虑一个结论是:偶数个点的树的形态确定之后,只有恰好 1 1 1 种染色方案,即从叶子一层一层往上面染,…...

用《斗破苍穹》的视角打开C#委托2 委托链 / 泛型委托 / GetInvocationList
委托链 经过不懈地努力,我终于成为了斗师,并成功掌握了两种斗技——八极崩和焰分噬浪尺。于是,我琢磨着,能不能搞一套连招,直接把对方带走。 using System; using System.Collections.Generic; using System.Linq; u…...

唐老师讲电赛
dc-dc电源布局要点...

[ICCV-23] DeformToon3D: Deformable Neural Radiance Fields for 3D Toonification
pdf | code 将3D人脸风格化问题拆分为几何风格化与纹理风格化。提出StyleField,学习以风格/ID为控制信号的几何形变残差,实现几何风格化。通过对超分网络引入AdaIN,实现纹理风格化。由于没有修改3D GAN空间,因此可以便捷实现Edit…...
配置Hive使用Spark执行引擎
配置Hive使用Spark执行引擎 Hive引擎概述兼容问题安装SparkSpark配置Hive配置HDFS上传Spark的jar包执行测试速度对比 Hive引擎 概述 在Hive中,可以通过配置来指定使用不同的执行引擎。Hive执行引擎包括:默认MR、tez、spark MapReduce引擎: 早…...
)
基于FPGA的视频接口之千兆网口(五应用)
简介 相信网络上对于FPGA驱动网口的开发板、博客、论坛数不胜数,为何博主需要重新手敲一遍呢,而不是做一个文抄君呢!因为目前博主感觉网络上描述的多为应用层上的开发,非从底层开始说明,本博主的思虑还是按照老规矩,按照硬件、底层、应用等关系,使用三~四篇文章,来详细…...
车载开发所学内容,有哪些?程序员的转岗位需求
一、高速发展的行业前景 随着全球智能汽车市场的飞速发展,车载开发行业的前景可谓一片光明。各国政府对于自动驾驶和智能交通系统的政策支持,为行业带来了前所未有的机遇。此外,人工智能、大数据、云计算等前沿技术的不断突破,为…...
VSCode Intellij IDEA CE 数据库连接
VSCode & Intellij IDEA CE 数据库连接 大概记一下现在正在用的几个工具/插件 VSCode VSCode 里面的工具我下载了很多,如果只是链接 MySQL 的话,可能用 Jun Han 这位大佬的 MySQL 就好了: 使用这个插件直接打开 .sql 文件单击运行就能…...

直流无刷电机开发应用
下面的链接是笔者在研究无刷电机的过程中,找到的业内无刷电机驱动龙头企业,峰岹科技的各类无刷电机应用设计参考,比较有学习和借鉴意义。 应用手册 - 峰岹科技...

c 语言基础题目:PTA L1-030 一帮一
“一帮一学习小组”是中小学中常见的学习组织方式,老师把学习成绩靠前的学生跟学习成绩靠后的学生排在一组。本题就请你编写程序帮助老师自动完成这个分配工作,即在得到全班学生的排名后,在当前尚未分组的学生中,将名次最靠前的学…...

网工内推 | base郑州,上市公司,最高15薪,五险一金全额缴
01 四方达 招聘岗位:网络工程师 职责描述: 1、负责公司数据中心(机房)的管理与运维工作。 2、负责公司服务器、路由器、防火墙、交换机等设备的管理、以及网络平台的运行监控和维护; 3、负责公司服务器运维管理工作、…...
求后缀表达式的值
后缀表达式的值 【题目描述】 从键盘读入一个后缀表达式(字符串),只含有0-9组成的运算数及加()、减(—)、乘(*)、除(/)四种运算符。每个运算数之间…...
【FISCO-BCOS】十七、角色的权限控制
目录 一、角色定义 二、账户权限控制 1.委员新增、撤销与查询 2.委员权重修改 3.委员投票生效阈值修改 4. 运维新增、撤销与查询 一、角色定义 分为治理方、运维方、监管方和业务方。考虑到权责分离,治理方、运维方和开发方权责分离,角色互斥。 治理…...

vue怎样封装接口
Vue可以使用axios来发送HTTP请求,通过封装axios可以实现接口的统一管理和调用。下面是一个简单的封装接口的示例。 安装axios 在项目中安装axios依赖,可以使用npm或者yarn命令进行安装。 npm install axios --save创建api.js文件 在项目中创建一个ap…...

Typescript 笔记:函数
1 函数定义 function function_name() {// 执行代码 }2 函数返回值 function function_name():return_type { // 语句return value; } return_type 是返回值的类型。 return 关键词后跟着要返回的结果。 返回值的类型需要与函数定义的返回类型(return_type)一致。 3 函数…...
Axios 封装
请注意以下文件夹: utils下的setToken.js 是token封装(封装 Token-CSDN博客),service.js 是axios封装。 Axios封装: 1.安装axios 在项目终端下 输入: npm install axios --save 2.在main.js全局引入axios import axios from axiosVue.prototype.$axios =axios //挂…...
Javascript的垃圾回收机制)
CocosCreator 面试题(一)Javascript的垃圾回收机制
JavaScript的垃圾回收机制是一种自动管理内存的机制,它负责检测和回收不再使用的内存,以便释放资源并提高性能。 标记清除(Mark and Sweep):这是JavaScript最常用的垃圾回收算法。它的工作原理是通过标记活动对象&…...

【计算机网络】UDP协议编写群聊天室----附代码
UDP构建服务器 x 预备知识 认识UDP协议 此处我们也是对UDP(User Datagram Protocol 用户数据报协议)有一个直观的认识; 后面再详细讨论. 传输层协议无连接不可靠传输面向数据报 网络字节序 我们已经知道,内存中的多字节数据相对于内存地址有大端和小端之分, 磁盘文件中的…...

Java架构师高并发架构设计
目录 1 导学2 什么是高并发问题3 高并发处理之道4 akf扩展立方体5 细化理念应对高并发5 总结1 导学 本章的主要内容是大型系统架构设计的难点之一,高并发架构设计相关的知识落到实际项目上,就是订单系统的高并发架构设计。我们首先会去学习到底何为高并发问题,先把问题搞清楚…...
)
【客观赋权法1】熵权法(MATLAB全代码)
熵权法(entropy weight method, EWM) 1 原理2 MATLAB代码3 案例参考赋权法(Weighting Method) 是一种常用的数据处理方法,它可以将不同变量之间的重要性进行区分,并赋予它们不同的权重,以反映它们对整体的贡献程度。 指标在评估体系中的重要程度可以用 指标权重系数表示…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...
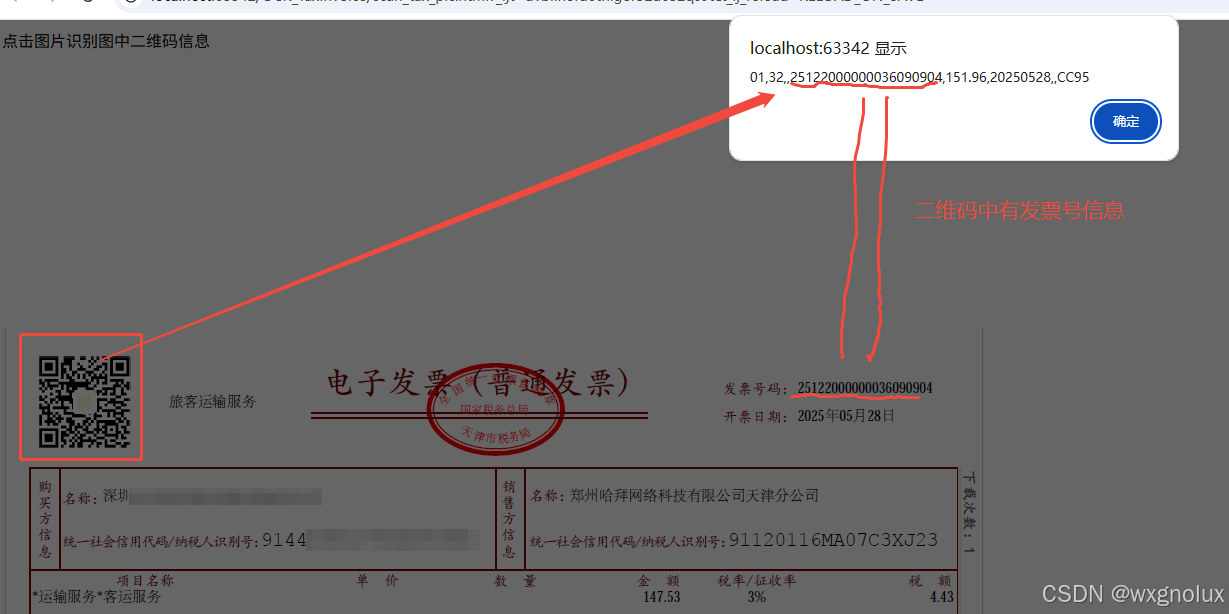
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
