希尔排序:优化插入排序的精妙算法
排序算法在计算机科学中扮演着重要的角色,其中希尔排序(Shell Sort)是一种经典的排序算法。本文将带您深入了解希尔排序,包括其工作原理、性能分析以及如何使用 Java 进行实现。

什么是希尔排序?
希尔排序,又称“缩小增量排序”,是插入排序的一种改进版本。它的核心思想是通过逐步缩小增量值,将较大的元素向数组的一端移动,以减少逆序对的数量,从而提高整体的有序性。
希尔排序的关键步骤包括:
- 选择一个递减的增量序列,通常以 n/2 为初始增量,然后依次将增量减小为 n/4、n/8,直到增量为 1。
- 对于每个增量值,将数组分成若干个子序列,每个子序列使用插入排序进行排序。
- 不断减小增量值,重复步骤 2,直到增量值为 1,此时进行最后一次插入排序,完成排序过程。
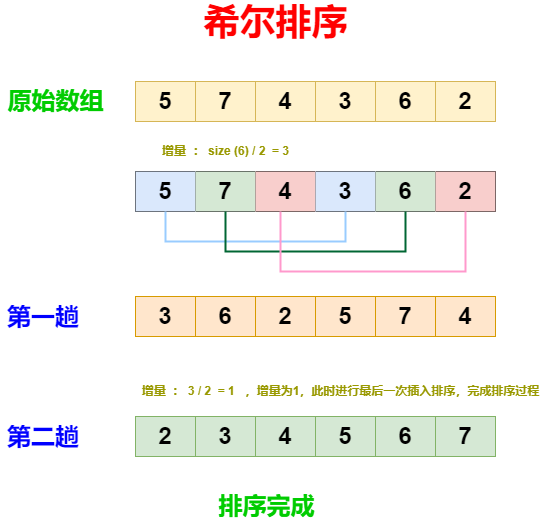
希尔排序的性能分析
希尔排序的性能分析相对复杂,因为它依赖于所选择的增量序列。以下是希尔排序性能的一般性分析:
- 最坏情况时间复杂度
希尔排序的最坏情况时间复杂度取决于增量序列的选择。使用希尔增量序列时,最坏情况时间复杂度为$ O(n^2)$,与插入排序相同。但使用某些增量序列,如 Hibbard 或 Knuth 序列,最坏情况时间复杂度可以降低到 O ( n ( 3 / 2 ) ) O(n^(3/2)) O(n(3/2))。
- 平均情况时间复杂度
希尔排序的平均情况时间复杂度通常介于 O ( n ( 1.25 ) ) 到 O ( n 2 ) O(n^(1.25)) 到 O(n^2) O(n(1.25))到O(n2) 之间,具体取决于增量序列的选择和数据分布。
- 空间复杂度
希尔排序的空间复杂度为 O(1),因为它只需要常数级别的额外空间来存储增量、临时变量等。
- 稳定性
希尔排序是不稳定的排序算法,因为在排序过程中,相等元素的相对顺序可能会发生改变。
Java 代码实现
public class Test {public static void main(String[] args) {int[] arr = new int[]{5,7,4,3,6,2};shellSort(arr);}public static void shellSort(int[] arr) {System.out.println("原始数组:"+ Arrays.toString(arr));//获取排序数组的长度int len= arr.length;//初始化增量为 len/2int initGap = len >> 1;//count排序不使用,只是为了打印循环的次数,加深理解int count = 1;//循环处理,不断减小增量值,直到增量值为 1,此时进行最后一次插入排序,完成排序过程for(int gap = initGap; gap > 0; gap >>=1){// 对每个子序列进行插入排序for(int i = gap; i < len; i++){int temp = arr[i];int j = i;while (j >= gap && arr[j-gap] > temp ){// 如果插入元素小于当前元素,则将当前元素后移一位arr[j] = arr[j - gap];//递减值为每次的增量j -= gap;}//将目标元素插入到正确的位置arr[j] = temp;}// 打印每趟排序完成后的数组状态,以便查看排序进度System.out.println("第"+count+"趟排序完成的数组:"+ Arrays.toString(arr));count++;}System.out.println("排序完成的数组:"+ Arrays.toString(arr));}}
运行结果:
原始数组:[5, 7, 4, 3, 6, 2]
第1趟排序完成的数组:[3, 6, 2, 5, 7, 4]
第2趟排序完成的数组:[2, 3, 4, 5, 6, 7]
排序完成的数组:[2, 3, 4, 5, 6, 7]
总结
希尔排序是一种优雅而高效的排序算法,尽管它相对于一些现代排序算法来说可能不够快,但它仍然具有重要的教育和历史价值。通过深入了解希尔排序的工作原理和实现方式,您可以更好地理解排序算法的核心原理,并在需要时选择适当的排序算法以提高程序性能。希望本文帮助您更好地理解希尔排序并激发您对排序算法的兴趣。
相关文章:

希尔排序:优化插入排序的精妙算法
排序算法在计算机科学中扮演着重要的角色,其中希尔排序(Shell Sort)是一种经典的排序算法。本文将带您深入了解希尔排序,包括其工作原理、性能分析以及如何使用 Java 进行实现。 什么是希尔排序? 希尔排序,…...

新能源电动汽车安全性能检测中采集车架号及BMS电池数据的难点
按照新能源电动汽车安全性能检测,必须采集到汽车的车架号及BMS电池数据做对应的评测。国内电动汽车主要以比亚迪、特斯拉、广汽埃安、五菱新能源、长安新能源、大众、理想、蔚来、哪吒等主流为主。与传统燃油车不同的是,电动汽车不用执行OBD2标准&#x…...

函数reshape(-1,)里的-1的意思
reshape函数是对narray的数据结构进行维度变换,由于变换遵循对象元素个数不变,在进行变换时,假设一个数据对象narray的总元素个数为N,如果我们给出一个维度为(m,-1)时,我们就理解为将…...

名词作形容词的用法
【名词作形容词的用法】 有考英语二的同学问我,为什么名词能修饰名词,比如spending proportion(支出比例), job satisfaction(工作满意度),之前老师不是说这种写法不能乱用么? 那我在这里简单说明一下“形…...
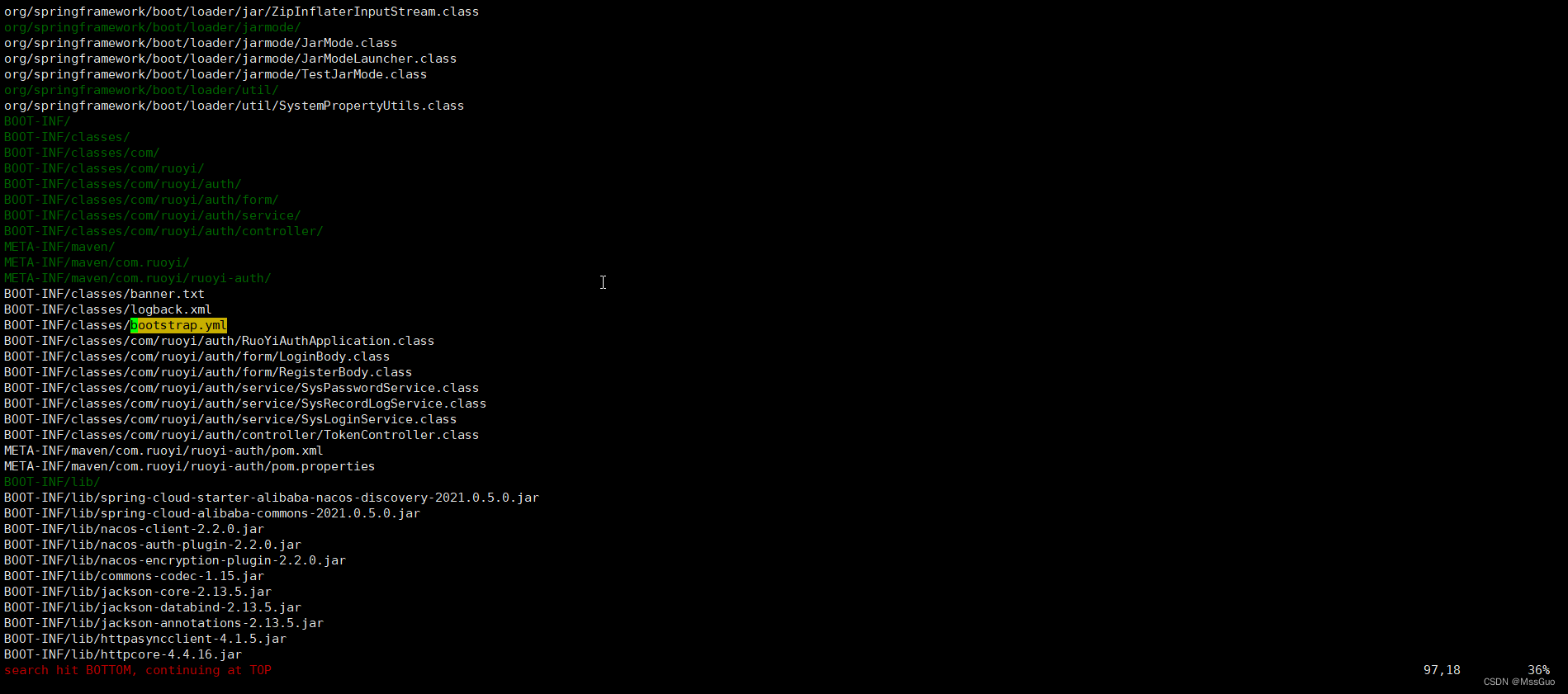
若依微服务部署,裸服务部署、docker部署、k8s部署
目录 前言windows 部署若依-微服务版本浏览器验证docker部署若依-微服务版本浏览器验证k8s部署若依-微服务版本浏览器验证总结 前言 环境:centos7、Win10 若依是一个合适新手部署练习的开源的微服务项目,本篇讲解Windows部署若依微服务、docker部署若依…...
【置顶】关于博客的一些公告
所谓 万事开头难,最开始的两个专栏 《微机》 和 《骨骼动作识别》 定价 29.9 ,因为: 刚开始确实比较困难,要把自己学的知识彻底搞懂讲给别人,还要 码字排版,从 Markdown 语法开始学起(这都是 花…...

Fastadmin后端表格动态展示列
前言 后端有多角色时, 往往有些表格中的列需要根据条件来根据角色身份决定是不是需要该角色查看, 为此就衍生出一个需要动态控制展示某列的需求fastadmin框架内调用的table实际上在初始化时, 可以修改columns中的visible属性来控制是否显示, 但是这个参数只能传入bool, 不能像…...

如何在ubnutu上安装docker
卸载旧版本 sudo apt-get remove docker docker-engine docker.io添加HTTPS传输软件包以及CA证书 sudo apt-get update sudo apt-get install \apt-transport-https \ca-certificates \curl \gnupg \lsb-release添加国内源以提升网速 添加软件源的GPG秘钥以确认所下载软件包…...
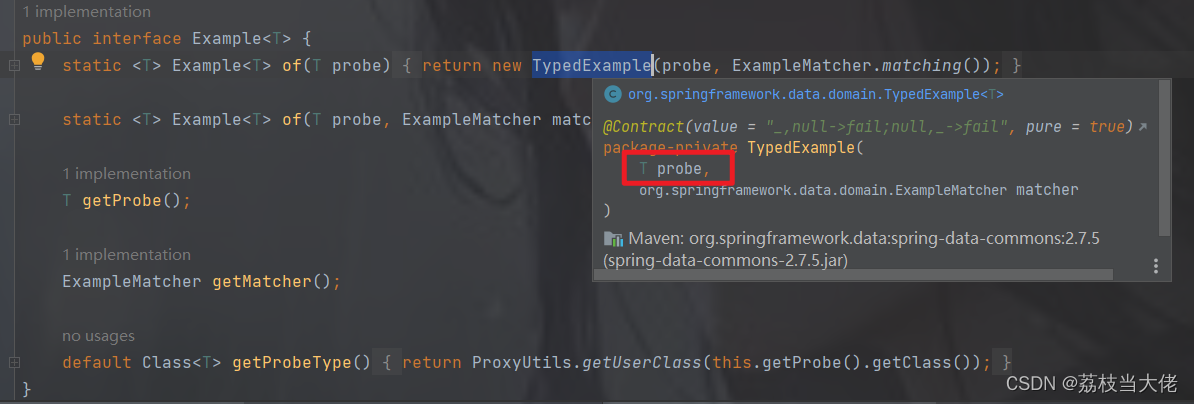
Mall脚手架总结(三) —— MongoDB存储浏览数据
前言 通过Elasticsearch整合章节的学习,我们了解SpringData框架以及相应的衍生查询的方式操作数据读写的语法。MongoDB的相关操作也同样是借助Spring Data框架,因此这篇文章的内容比较简单,重点还是弄清楚MongoDB的使用场景以及如何通过Sprin…...
Maven 引入外部依赖
如果我们需要引入第三方库文件到项目,该怎么操作呢? pom.xml 的 dependencies 列表列出了我们的项目需要构建的所有外部依赖项。 要添加依赖项,我们一般是先在 src 文件夹下添加 lib 文件夹,然后将你工程需要的 jar 文件复制到 …...

BS EN 12104-2023 软木地砖检测
软木地砖是指含有烧结成分的软木制成的块状砖,可用于地面覆盖物,装饰层等,具有脚感柔软舒适,防滑性能好,静音等性能,同时也其耐磨性较差,不易清洁。 BS EN 12104-2023软木地砖测试 测试项目 测…...
用Nginx搭建一个可用的静态资源Web服务器
sudo wget http://dlib.net/files/dlib-19.24.tar.bz2下载需要的文件。 sudo tar jxf dlib-19.24.tar.bz2进行解压。 sudo mkdir /nginx/dlib在nginx安装目录/nginx创建一个新的目录dlib。 配置文件nginx.conf里边的内容如下: worker_processes 1; events {…...
MAX30102心率血氧传感器
MAX30102心率血氧传感器介绍 背景基本功能基本结构基本原理采集方法直通式采集方法反射式采集方法 血氧采集原理Beer-Lambert 定理皮肤组织模型血氧测量过程AC / DC 的计算 心率采集原理 实验结果代码走读资源链接 背景 目前,基本上所有的可穿戴式设备都集成了心率…...

高效解决 TypeError : ‘ numpy._DTypeMeta‘ object is not subscriptable 问题
文章目录 问题描述解决问题 问题描述 解决问题 参考博文 打开报错位置 AppData\Roaming\Python\Python39\site-packages\cv2\typing\ 添加single-quotes,即单引号 博主说The trick is to use single-quotes to avoid the infamous TypeError: ‘numpy._DTypeMeta’…...
)
Hadoop作业篇(一)
一、选择题 1. 以下哪一项不属于Hadoop可以运行的模式__C____。 A. 单机(本地)模式 B. 伪分布式模式 C. 互联模式 D. 分布式模式 C. 互联模式 不属于Hadoop可以运行的模式。 Hadoop主要有四种运行模式: A. 单机(本地…...
)
SpringCloud中的分布式锁用法详解(Java+Redis SETNX命令)
前言: 在分布式系统中,保证数据的一致性和并发控制是至关重要的。分布式锁能够解决多个进程/线程同时访问共享资源的问题,确保只有一个进程/线程能够获得锁。本文将介绍如何使用Java和Redis实现分布式锁,并提供示例代码和注意事项…...

初学者如何选择:前端开发还是后端开发?
#开发做前端好还是后端好【话题征文】# 作为一名有多年开发经验的过来人,我认为前端开发和后端开发都有其独特的魅力和挑战。下面我将就我的个人经历和观点来分享一些关于前端开发和后端开发的看法。 首先,让我们将编程世界的大城市比作前端开发和后端开…...

从php页面插入MySQL的数据变为乱码如何解决?
在 PHP 页面中向 MySQL 数据库插入数据时,如果数据出现乱码,可能是因为字符集设置不正确或者字符编码不匹配。 数据库字符集设置不正确: 确保数据库的字符集设置与您的应用程序所使用的字符集一致。通常情况下,UTF-8 是一个通用的…...
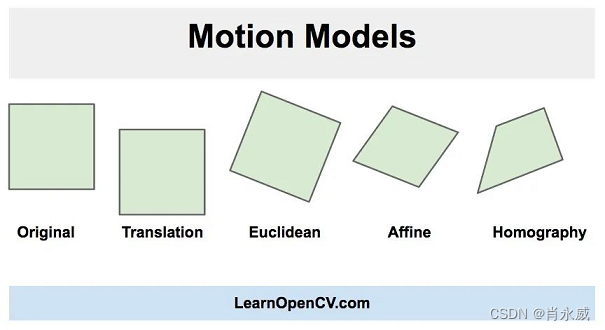
OpenCV防抖实践及代码解析笔记
视频防抖是指用于减少摄像机运动对最终视频的影响的一系列方法。摄像机的运动可以是平移(比如沿着x、y、z方向上的运动)或旋转(偏航、俯仰、翻滚)。 正如你在上面的图片中看到的,在欧几里得运动模型中,图像…...

函数栈帧的创建与销毁剖析
目录 一、前言 二、基础知识介绍 2.1 寄存器介绍 2.2、汇编指令介绍 三、函数栈帧的创建销毁过程 3.1 调用main函数的函数 3.2 main函数开辟栈帧 3.3 在main函数中创建变量 3.4 调用Add函数前的准备 3.5 为Add函数开辟栈帧 3.6 在Add函数中创建变量并运算 3.7 Add函…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
