【算法|双指针系列No.4】leetcode11. 盛最多水的容器
个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
点解直接跳转到该题目
目录
- 1️⃣题目描述
- 2️⃣算法分析
- 3️⃣代码编写
1️⃣题目描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例1:
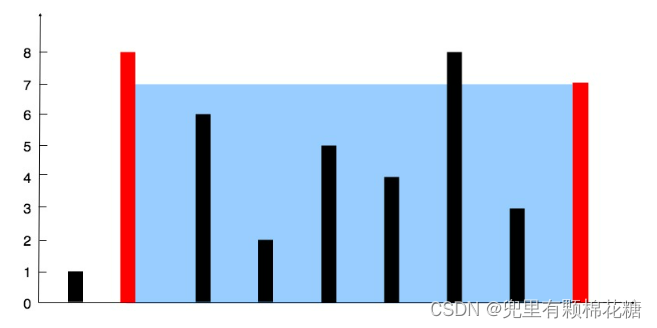
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例2:
输入:height = [1,1]
输出:1
注意:
n == height.length2 <= n <= 1050 <= height[i] <= 104
2️⃣算法分析
通过不断地调整较短的边界来寻找可能的最大容量。因为容器的容量受限于较短的边界,所以选择移动较短的边界可以增加容器的高度,有可能得到更大的容量。通过不断缩小指针之间的宽度,直到指针重合,即可得到最大容量。
容器容量:v = s * h,由于我们这里不断移动两个“指针”,所以 s 是不断变小的,那么问题来了,我们要移动哪个指针呢(是向右移动左指针的,还是向左移动右指针呢?),我们要知道无论我们移动哪一个指针容器的 s 都是减小的,此时如果要使得容器容量增大,我们需要移动指针指向的值较小的那个指针。举个例子(1,9),我们此时就需要向右移动左指针了,因为我们只有移动左指针才有可能使得容器的容器容量变大(即通过增加h的方式)。
即:
if(height[l] < height[r]) l++;
else r--;
3️⃣代码编写
class Solution {
public:int maxArea(vector<int>& height) {int l = 0,r = height.size() - 1,ret = 0;while(l < r){int v = (r - l) * min(height[l],height[r]);ret = max(v,ret);if(height[l] < height[r]) l++;else r--; }return ret;}
};
相关文章:
【算法|双指针系列No.4】leetcode11. 盛最多水的容器
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

数据结构全集介绍
以下列举了部分常见的数据结构: 数组(Array):数组是一种线性数据结构,可以用来存储固定大小的数据集合。在数组中,每个元素都有一个对应的索引,可以通过索引直接访问和更新元素。数组的优点是访…...

力扣刷题-字符串-反转字符串
344 反转字符串 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。 不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。 你可以假设数组中的所有字符都是 ASCII 码表中…...

【CCNP】第七章 动态路由协议-BGP
第一节 BGP的基本概念 BGP(Border Gateway Protocol),边界网关协议 是运行在网络和网络之间的协议,是一款EGP(外部网关协议) BGP基于TCP协议工作,目的端口号179。源端口随机,由路由…...
)
java学习--day24(stream流)
文章目录 今天的内容1.Stream【难点】1.1获取流的对象1.2Stream流对象下面1.2.1count和forEach1.2.2filter方法1.2.3limit1.2.4map方法1.2.5skip1.2.6concat 1.3收集流 1.基于接口和抽象类的匿名内部类的写法 abstract class Person {public abstract void eat(); } public sta…...

Multi-Grade Deep Learning for Partial Differential Equations
论文阅读:Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation符号定义偏微分方程定义FNN定义PI…...

Docker部署rustdesk
查看镜像版本 https://hub.docker.com/r/rustdesk/rustdesk-server/tags 拉取镜像 docker pull rustdesk/rustdesk-server:1.1.8-2创建挂载目录 mkdir -p /opt/rustdesk/{hbbr,hbbs}/root运行hbbs –nethost 仅适用于 Linux,它让 hbbs/hbbr 可以看到对方真实的…...

win1011安装MG-SOFT+MIB+Browser+v10b
文章目录 安装MG-SOFTSNMP服务配置安装MG-SOFT启动MIB-Browser以及错误解决MIB Browser使用 安装MG-SOFT win10和win11安装基本一样,所以参照下面的操作即可! SNMP服务配置 打开设置,应用和功能,可选功能,选择添加功…...
)
PCL点云处理之Pcd文件读取、法线与曲率计算、多线程加速、属性字段合并 (二百零八)
PCL点云处理之Pcd文件读取、法线与曲率计算、多线程加速、属性字段合并(二百零八) 一、相关介绍二、算法实现1.代码一、相关介绍 (夜深人不静) 法线和曲率的计算是点云处理中常用的关键特征,PCL提供了特有的点类型PointNormal来记录这些信息,通过OMP多线程对相关的计算函…...
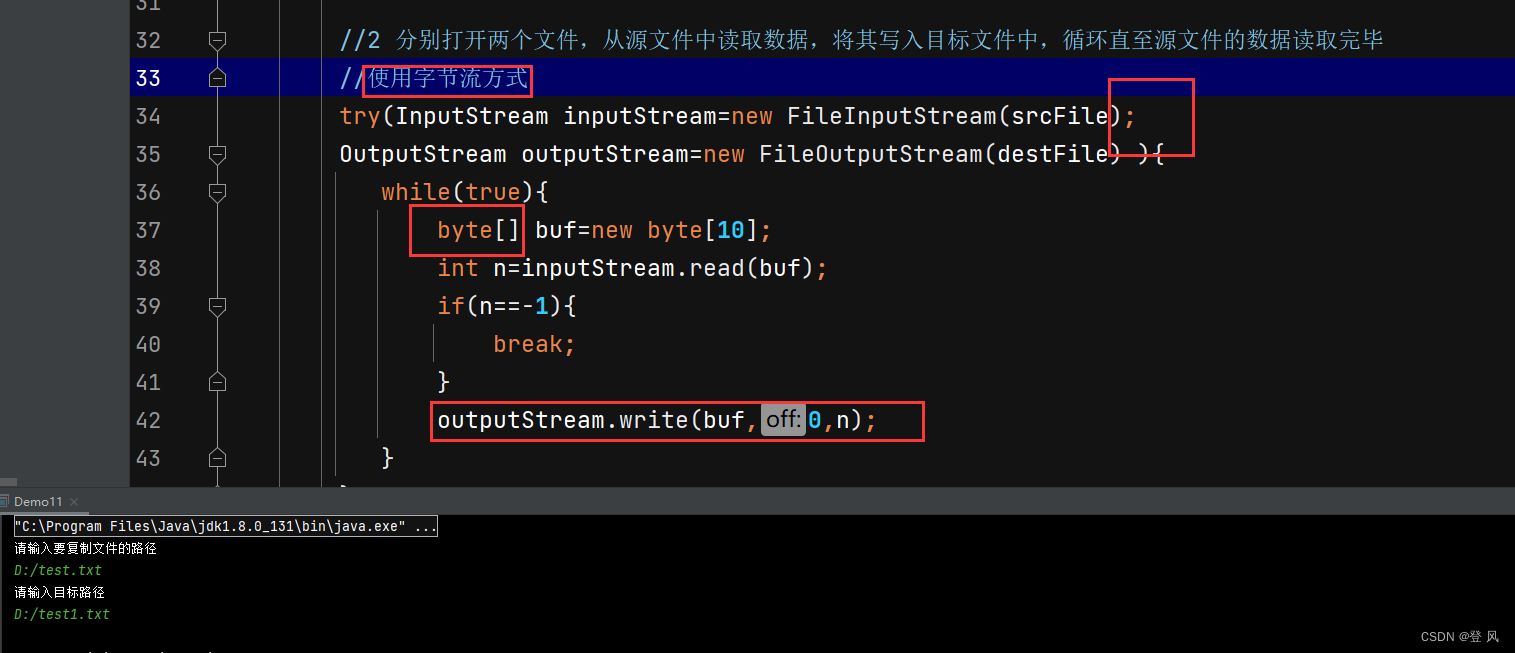
JavaEE-文件IO操作
构造方法 一般方法,有很多,我们以下只是列举几个经常使用的 注意在上述的操作过程中,无论是绝对路径下的这个文件还是相对路径下的这个文件,都是不存在的 Reader 使用 --> 文本文件 FileReader类所涉及到的一些方法 Fil…...

二蛋赠书四期:《Go编程进阶实战:开发命令行应用、HTTP应用和gRPC应用》
前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,每一位技术人员都对自己的技能提升和职业发展有着热切的期待。因此,我非常感激大家一直…...
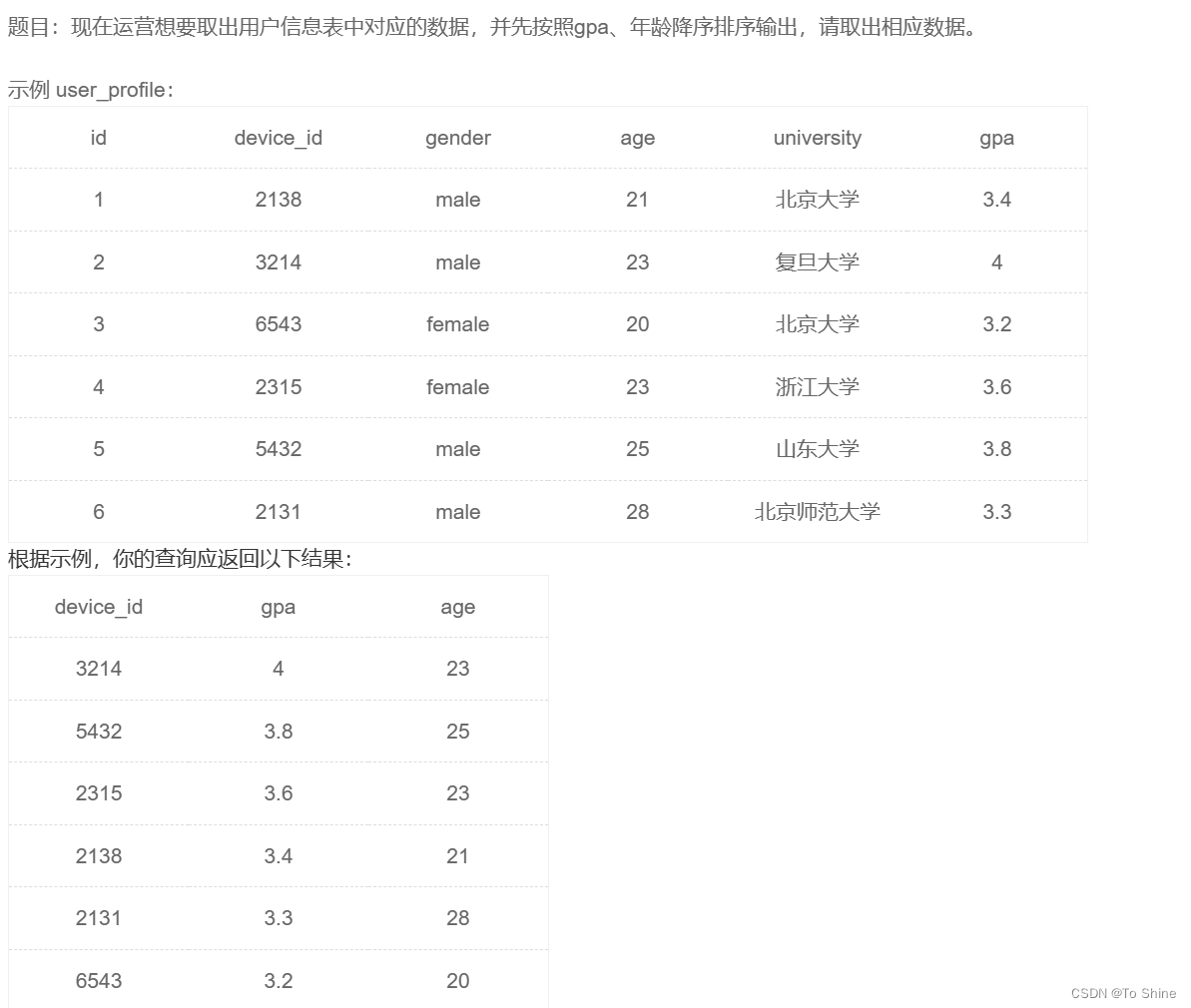
MySQL数据库基本操作-DQL-排序查询
介绍 如果我们需要对读取的数据进行排序,我们就可以使用 MySQL 的 order by 子句来设定你想按哪个字段哪种方式来进行排序,再返回搜索结果。 语法 select 字段名1,字段名2,…… from 表名 order by 字段名1 [asc|desc]…...

这是一篇测试文章
这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章…...

Ubuntu plt画图 新罗马字体网格marker刻度朝内
* 字体文件:坚果云下code包,新罗马字体 参考链接:Linux下Matplotlib画图New Times Roman字体设置 - 知乎 * 刻度朝内 plt.rcParams[font.sans-serif] [Times New Roman]plt.rcParams[xtick.direction]in#设置x轴刻度向内plt.rcParams[ytic…...

flutter布局中的一些细节
前言 记录flutter使用中遇到的一些细节和坑,希望能帮助到大家 Column中不能直接嵌套ListView, (需要指定ListView的高度或者加上shrinkWrap: true属性)需要限制button的大小,可以在外部嵌套一个Container或SizedBox来限制在List…...
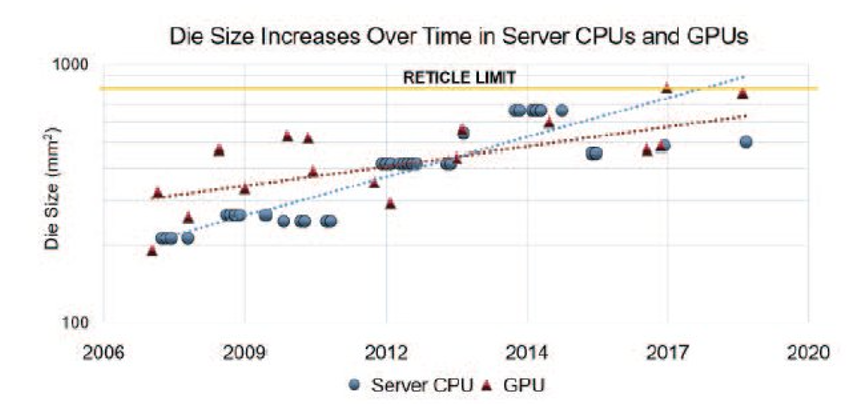
论文解析——AMD EPYC和Ryzen处理器系列的开创性的chiplet技术和设计
ISCA 2021 摘要 本文详细解释了推动AMD使用chiplet技术的挑战,产品开发的技术方案,以及如何将chiplet技术从单处理器扩展到多个产品系列。 正文 这些年在将SoC划分成多个die方面有一系列研究,MCM的概念也在不断更新,AMD吸收了…...

第二证券:汽车产业链股活跃,恒勃股份、博俊科技“20cm”涨停
轿车产业链股9日盘中走势活跃,截至发稿,恒勃股份、博俊科技“20cm”涨停,德迈仕涨超17%,上声电子涨超14%,川环科技涨超10%,圣龙股份、科华控股、沪光股份、上海沿浦、日盈电子、赛力斯等均涨停。 工作方面…...

孙帅Spring源码
【视频来源于:B站up主孙帅suns Spring源码视频】【微信号:suns45】...

jenkins工具系列 —— 插件 使用Changelog获取commit记录
文章目录 安装changelog插件重启jenkins配置 ChangelogExecute shell 使用 changelog邮件中html格式也可以使用构建测试(查看构建项 -> 控制台输出) 安装changelog插件 插件文件可通过 V 获取 点击 左侧的 Manage Jenkins —> Plugins ——> …...
【JavaScript】浅拷贝与深拷贝
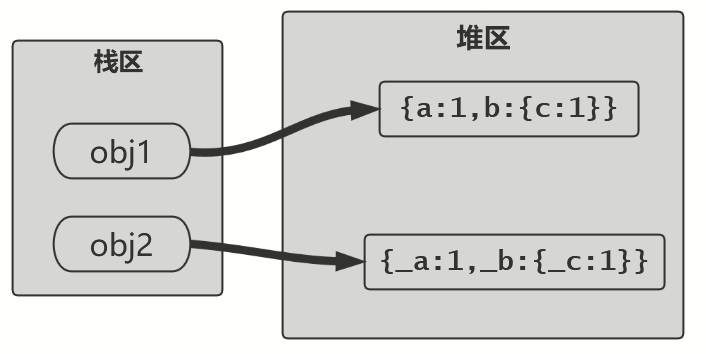
引言 浅拷贝、深拷贝是对引用类型而言的。 引用类型的变量对应一个栈区地址,这个栈区地址处存储的值是存放的真正的数据的堆区地址。 基本数据类型的变量也对应一个栈区地址,但是该地址存储的是其真正的值。 let a b发生了什么? let obj…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

