归纳所猜半结论推出完整结论:CF1592F1
https://www.luogu.com.cn/problem/CF1592F1
场上猜了个结论,感觉只会操作1。然后被样例1hack了。然后就猜如果 ( n , m ) (n,m) (n,m) 为1则翻转4操作,被#14hack了。然后就猜4操作只会进行一次,然后就不知道怎么做下去了。
上面猜的结论都正确,但是既然猜结论了,为什么不考虑先证明一波?
考虑2次操作4,代价为6,只有两种情况:
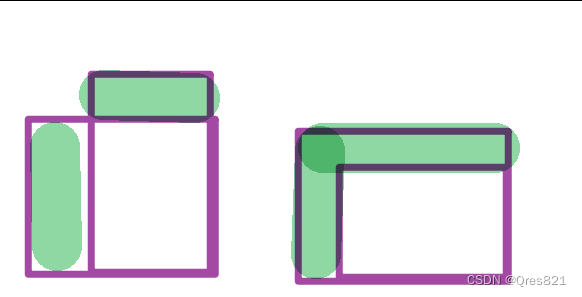
而他们都可以用操作1表示出来。
然后考虑怎么做。其实感觉没有操作4时,每个位置是否翻转都可以直接O(1)算出来。但这存在一定难度。
我当时写的是:

这样子存在逻辑联系,不方便直接表示,所以应该考虑把if取得。
怎么去?就多列几个表示出来。(相当于多一个媒介)
v i , j = a i , j ⊗ s i − 1 , j ⊗ s i , j − 1 ⊗ s i − 1 , j − 1 p i , j = v i , j ⊗ s i − 1 , j ⊗ s i , j − 1 ⊗ s i − 1 , j − 1 v_{i,j}=a_{i,j}\otimes s_{i-1,j}\otimes s_{i,j-1}\otimes s_{i-1,j-1}\\p_{i,j} = v_{i,j}\otimes s_{i-1,j}\otimes s_{i,j-1}\otimes s_{i-1,j-1} vi,j=ai,j⊗si−1,j⊗si,j−1⊗si−1,j−1pi,j=vi,j⊗si−1,j⊗si,j−1⊗si−1,j−1
然后我们发现了 s s s 和 a a a 相同。
然后发现翻转4只会改变4个位置。
然后操作4有贡献只当这4个位置同时改变。
#include<bits/stdc++.h>
using namespace std;
//#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//#define M
//#define mo
#define N 510
int n, m, i, j, k, T;
int a[N][N], p[N][N], ans;
char str[N]; signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// srand(time(NULL));
// T=read();
// while(T--) {
//
// }auto calc = [&] (int x, int y) -> int {return a[x][y]^a[x+1][y]^a[x][y+1]^a[x+1][y+1]; }; n=read(); m=read(); for(i=1; i<=n; ++i) {scanf("%s", str+1); for(j=1; j<=m; ++j) if(str[j]=='B') a[i][j]=1; }for(i=n; i>=1; --i) for(j=m; j>=1; --j) {p[i][j]=(p[i+1][j]^p[i][j+1]^p[i+1][j+1]); if(a[i][j]^p[i][j]) p[i][j]^=1, ++ans; ans+=calc(i, j); if(i!=n && j!=m && calc(i, j) && calc(i, m) && calc(n, j) && calc(n, m)) k=-1; }printf("%d", ans+k); return 0;
}相关文章:

归纳所猜半结论推出完整结论:CF1592F1
https://www.luogu.com.cn/problem/CF1592F1 场上猜了个结论,感觉只会操作1。然后被样例1hack了。然后就猜如果 ( n , m ) (n,m) (n,m) 为1则翻转4操作,被#14hack了。然后就猜4操作只会进行一次,然后就不知道怎么做下去了。 上面猜的结论都…...
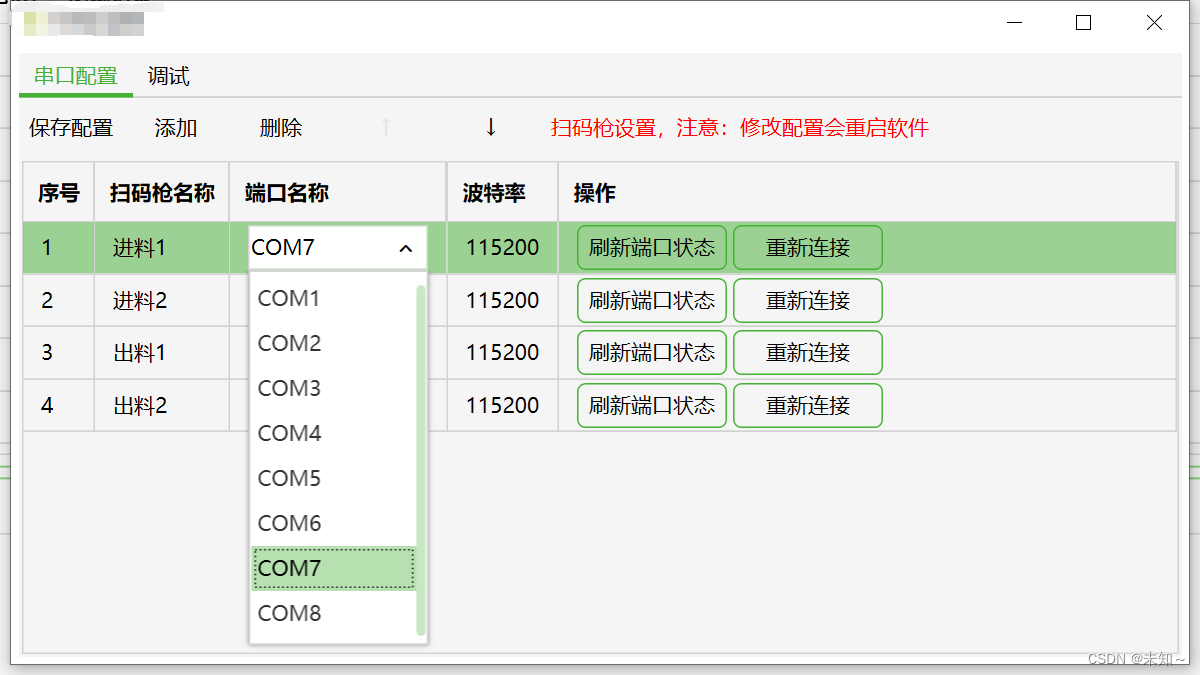
WPFdatagrid结合comboBox
在WPF的DataGrid中希望结合使用ComboBox下拉框,达到下拉选择绑定的效果,在实现的过程中,遇到了一些奇怪的问题,因此记录下来。 网上能够查询到的解决方案: 总共有三种ItemSource常见绑定实现方式: 1.ItemS…...

Markdown类图之继承、实现、关联、依赖、组合、聚合总结(十五)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

@MultipartConfig注解
前言: 在学习Javaweb的Servlet文件上传和下载的过程中,我们会遇到一个特殊的注解---MultipartConfig。 MultipartConfig的适用情况: 1.文件上传: 当您的应用程序需要接收用户上传的文件时,可以在相应的 Servlet 上使用 Multipart…...
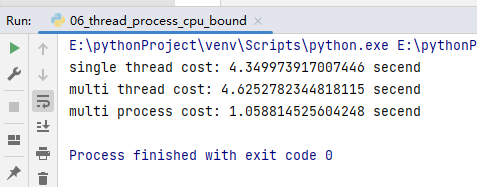
Python并发编程简介
1、Python对并发编程的支持 多线程: threading, 利用CPU和IO可以同时执行的原理,让CPU不会干巴巴等待IO完成多进程: multiprocessing, 利用多核CPU的能力,真正的并行执行任务异步IO: asyncio,在单线程利用CPU和IO同时执行的原理,实现函数异步执行使用Lo…...

WebSocket介绍及部署
WebSocket是一种在单个TCP连接上进行全双工通信的协议,其设计的目的是在Web浏览器和Web服务器之间进行实时通信(实时Web)。 WebSocket协议的优点包括: 1. 更高效的网络利用率:与HTTP相比,WebSocket的握手…...
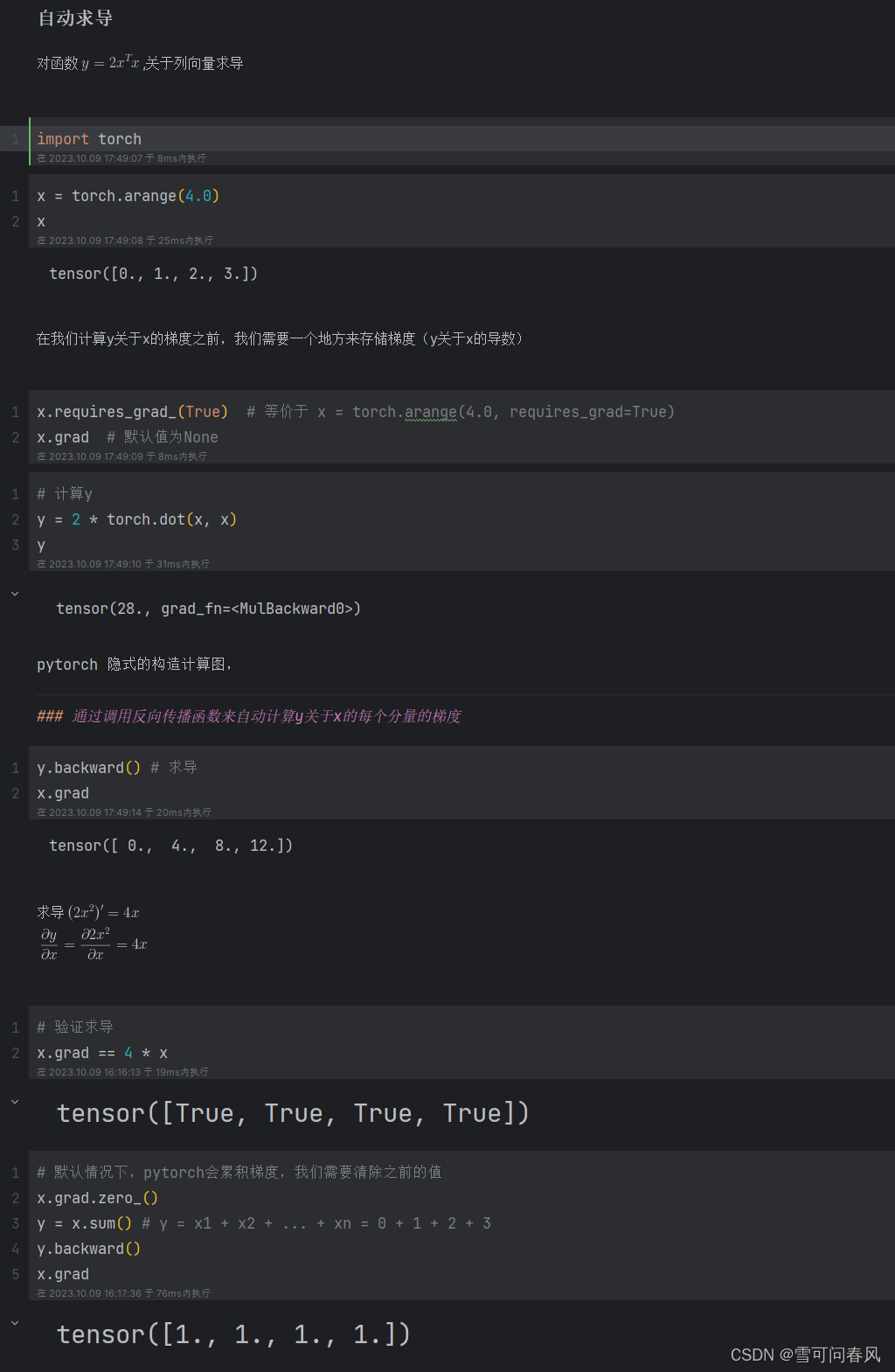
自动求导,计算图示意图及pytorch实现
pytorch实现 x1 torch.tensor(3.0, requires_gradTrue) y1 torch.tensor(2.0, requires_gradTrue) a x1 ** 2 b 3 * a c b * y1 c.backward() print(x1.grad) print(y1.grad) print(x1.grad 6 * x1 * y1) print(y1.grad 3 * (x1 ** 2))输出为: tensor(36.) …...

睿伴科创上线了
Robotutor睿伴,一个专业的青少儿编程科创教育品牌和科创服务平台。 Robotutor睿伴拥有一个超过5年的青少儿编程科创教育团队,积累了丰富的课程研发,教学服务和赛事辅导经验。并和上海多所知名高校、上海市计算机学会、上海青少年科学社等开展…...

域名抢注和域名注册
随着互联网的发展,域名已经成为了企业和个人在网络上展示自己的重要标志。如何获得一段好记、易拼写、有意义的域名,是很多人都面临的问题。本文将介绍域名抢注和域名注册的相关内容,并推荐ym.qqmu.com这个可靠的域名注册平台。 一、什么是域…...
【20】c++设计模式——>组合模式
组合模式定义 C组合模式(Composite Pattern)是一种结构型设计模式,他允许将对象组合成树形结构来表示“部分-整体”的层次结构;在组合模式中有两种基本类型的对象:叶子对象和组合对象,叶子对象时没有子对象…...

Jetpack:004-如何使用文本组件
文章目录 1. 概念介绍2. 使用方法2.1 通用参数2.2 专用参数 3. 示例代码4. 内容总结 我们在上一章回中介绍了Jetpack组件在布局中的对齐方式,本章回中主要介绍文 本组件的使用方法。闲话休提,让我们一起Talk Android Jetpack吧 1. 概念介绍 我们在本章…...
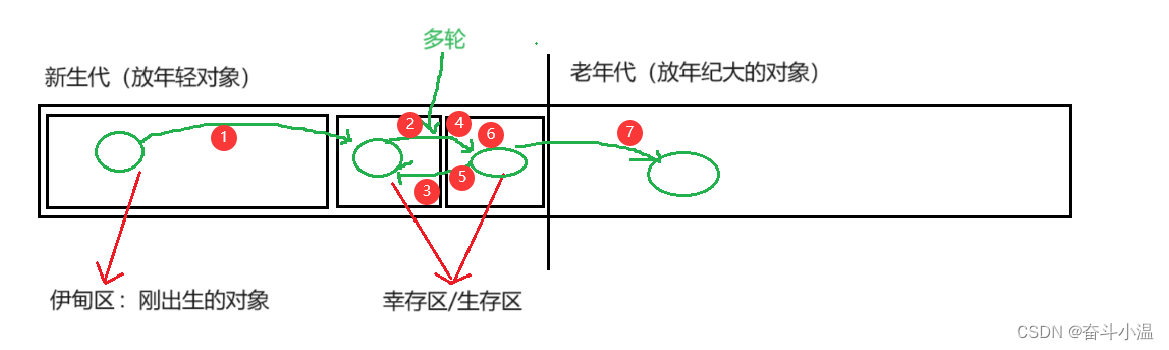
JVM(八股文)
目录 一、JVM简介 二、JVM中的内存区域划分 三、JVM加载 1.类加载 1.1 加载 1.2 验证 1.3 准备 1.4 解析 1.5 初始 1.6 总结 2.双亲委派模型 四、JVM 垃圾回收(GC) 1.确认垃圾 1.1 引用计数 1.2 可达性分析(Java 采用的方案&a…...

C#WPF标记扩展应用实例
本文介绍C#WPF标记扩展应用实例 一、标记扩展 标记扩展是一个 XAML 语言概念。 用于提供特性语法的值时,大括号({ 和 })表示标记扩展用法。 此用法指示 XAML 处理不要像通常那样将特性值视为文本字符串或者可转换为字符串的值。就是类似于值用变量的意思。 WPF 应用编程中…...
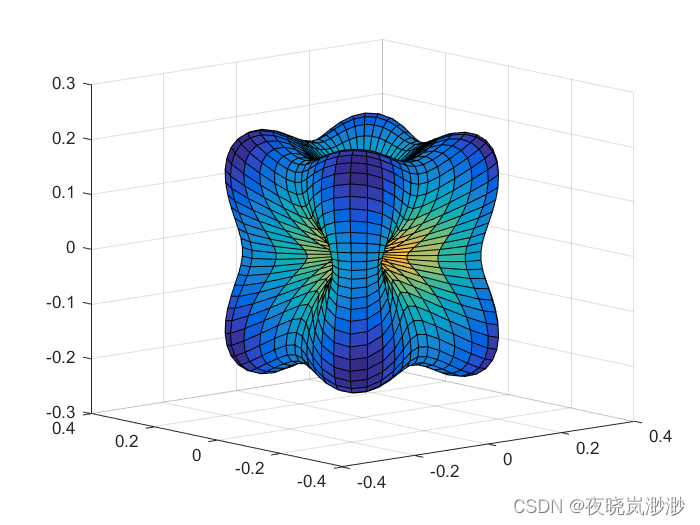
四维曲面如何画?matlab
clc; clear all [theta,phi]meshgrid(linspace(0,pi,50),linspace(0,2*pi,50)); zcos(theta); xsin(theta).*cos(phi); ysin(theta).*sin(phi); f-1*((x.*y).2(y.*z).2(z.*x).^2); surf(sin(theta).*cos(phi).*f,sin(theta).*sin(phi).*f,cos(theta).*f,f) 结果...
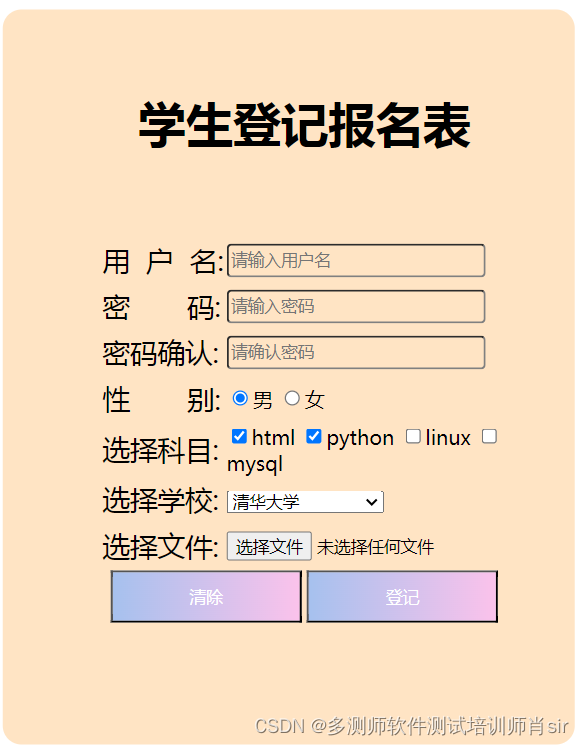
软件培训测试高级工程师多测师肖sir__html之作业11
html之作业 案例1: 截图: 代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>表单</title></head><body><table style"background-color:red" bo…...
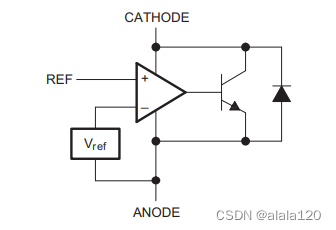
详解一典型的反激式开关电源方案
理解一个单端反激式开关电源方案: 1、抛出问题: 如图,在某系统方案上看到下图所示的单端反激式开关电源方案。 2、解析问题: 2.1、乍一看: 典型的AC-DC电路,考虑了安规及过压过流保护,如&am…...
)
AI 大框架基于python来实现基带处理之TensorFlow(信道估计和预测模型,信号解调和解码模型)
AI 大框架基于python来实现基带处理之TensorFlow(信道估计和预测模型,信号解调和解码模型) 基带处理(Baseband Processing)是一种信号处理技术,用于在通信系统中处理和调制基带信号。基带信号是指未经过调制的信号,通常包含原始数…...

阿里云上了新闻联播
我是卢松松,点点上面的头像,欢迎关注我哦! 阿里新任的CEO吴泳铭上央视新闻联播了! 在昨天的新闻联播里,出席科技座谈会,有一个特别镜头,出现了阿里新任CEO吴泳铭的镜头。 这个信号意义明显,我…...

算法练习12——跳跃游戏
LeetCode 55 跳跃游戏 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 贪…...

Java架构师系统架构设计服务拆分
目录 1 服务拆分和子系统模块拆分1.1 服务化架构的优势2 描绘系统蓝图里面的详解服务2.1 为什么拆分服务3 服务拆分的基本要求3.1 服务功能是自包含的3.2 服务呢应该具备独立性和专业性3.3 服务是无状态的3.4 服务之间采用轻量级的通讯机制4 服务拆分的基本方法4.1 按业务边界拆…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
